李宏毅机器学习特训营-机器学习作业1-PM2.5预测

可以学习课程内容李宏毅机器学习特训营

数据集介绍

本次作业使用丰原站的观测记录，分成 train set 跟 test set，train set 是丰原站每个月的前 20 天所有资料。test set 则是从丰原站剩下的资料中取样出来。

train.csv: 每个月前 20 天的完整资料。
test.csv : 从剩下的资料当中取样出连续的 10 小时为一笔，前九小时的所有观测数据当作 feature，第十小时的 PM2.5 当作 answer。一共取出 240 笔不重复的 test data，请根据 feature 预测这 240 笔的 PM2.5。

Data 含有 18 项观测数据 AMB_TEMP, CH4, CO, NHMC, NO, NO2, NOx, O3, PM10, PM2.5, RAINFALL, RH, SO2, THC, WD_HR, WIND_DIREC, WIND_SPEED, WS_HR。

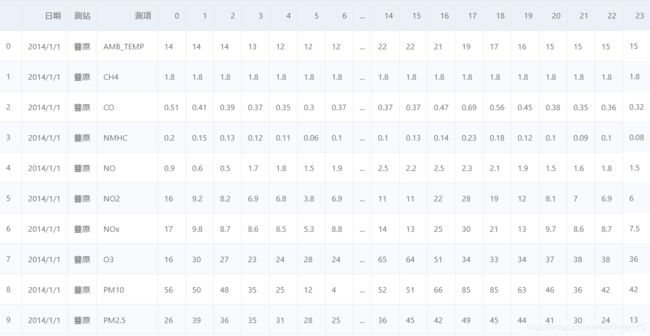
先读取文件看一下数据

import pandas 
import numpy as np
train_path = "work/hw1_data/train.csv"
test_path = "work/hw1_data/test.csv"
train_df = pandas.read_csv(train_path,encoding = 'big5')
#把“NR”都替换为数字0
train_df = train_df.replace("NR",0.0)
train_df[0:50]

数据如下

这里要删除前三列

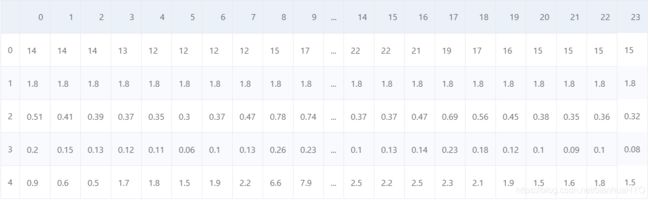
train_df = train_df.iloc[:,3:]
train_df.head()

数据如下

数据处理

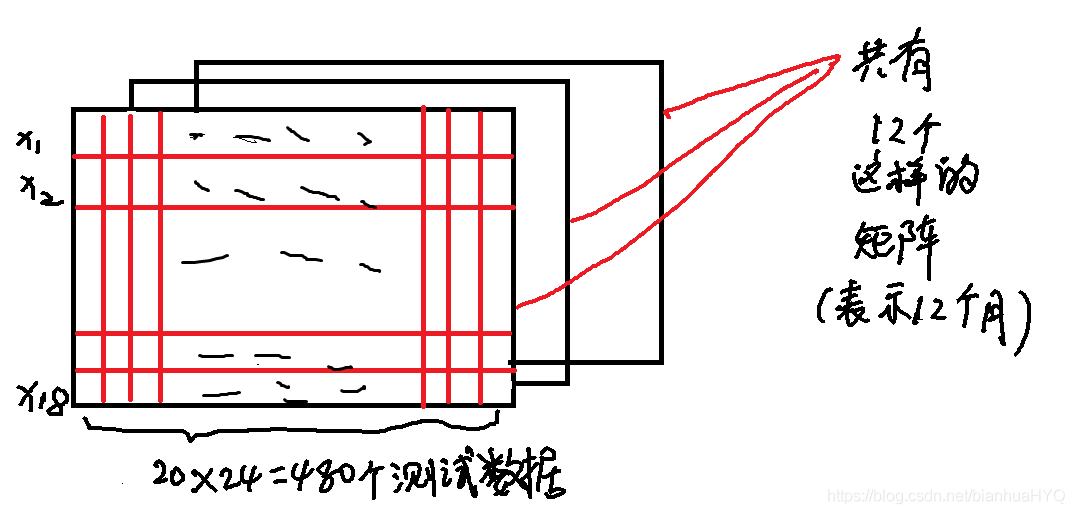
经过上面简单的处理后，下面就可以进行数据划分了。原始数据里，一天中对每个特征测试24次，每小时测一次，然后一个月是20天。在这里，我们可以把一个月（20天）中每个特征的数据整合到一起。先构造了一个三维矩阵 arr=np.empty([12,18,480]）， 含义是有12个月，18个特征 每个特征480（24*20=480）个数据

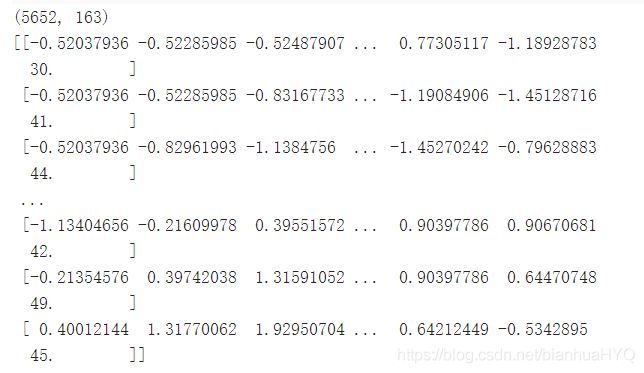
r_data = train_df.to_numpy()
print(r_data)
arr = np.empty([12,18,480], dtype = float)#构造三维矩阵  含义12个月，18个特征 每个特征480个数据   
print(arr.shape)

for m in range(12):
    for d in range(20):
        arr[m,:,d*24:(d+1)*24] = r_data[d*18:(d+1)*18,0:24]
print(arr.shape)  
print(arr[0:2,:,:])

打印如下

经过上面的数据整合后，下面是对数据进行分割，分为x与y_hat，y_hat是pm2.5的真实数据。x是特征数据，其行是18（特征个数），列是12个月乘以471 = 5652。 这里解释一下上面的471是怎么来的。

根据作业要求，需要根据前九个小时的特征数据预测第十个小时的pm2.5的值，现在我们已经知道一个月有20乘以24 = 480个数据， 且这480个数据是连续测到的，所以可以把这480个数据进行下图中的处理。

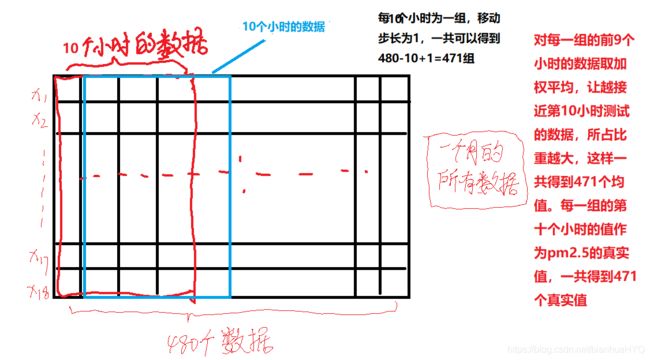
用加权平均，让越接近第10小时测试的数据，所占比重越大。后来训练效果并不好。。。

因为有12个月，把这些数据都整合在一起后，就是12*471=5652，也就是x的列数。y_hat也就对应有5652个真实数据。

后面也有尝试用 未经过加权平均处理的特征数据的方法，就是把前九个小时的所有数据都作为输入。 经过下面两个实验，发现经过加权平均处理后，训练误差和测试误差都比较高

最后决定选择不用加权平均，把前九个小时的所有数据都作为输入

下面的代码用加权平均处理特征数据（最后没有采用）

x = np.zeros([5652,18], dtype = float) #12*471=5652
r_x = np.zeros([18,9], dtype = float)
y_hat = np.zeros([5652,1], dtype = float)
a = np.zeros([1,18],dtype = float)
for m in range(12):
    for i in range(471):
        r_x[:,:] = arr[m,:,i:(i+9)]
        y_hat[(m*471+i)] = arr[m,9,i+9]
        a = np.average(r_x[:,:],axis=1,weights=(0.03, 0.05, 0.07,0.09,0.11,0.13,0.15,0.17,0.2)) #加权平均
        a=a.reshape((18,1))
        x[m*471+i,:]=a[:,0]
print(x.shape)
print(x)
print(y_hat.shape)
print(y_hat)

打印如下：

下面代码没有用加权平均处理特征数据，那么一组特征数据就有18*9=162维（最后采用的方法）

x = np.zeros([5652,162], dtype = float)# 12*471=5652,18*9=162
r_x = np.zeros([18,9], dtype = float)
y_hat = np.zeros([5652,1], dtype = float)
a = np.zeros([1,162],dtype = float)
for m in range(12):
    for i in range(471):
        r_x[:,:] = arr[m,:,i:(i+9)]
        y_hat[(m*471+i)] = arr[m,9,i+9]
        a = r_x.flatten()
        x[m*471+i,:]=a
print(x.shape)
print(x)
print(y_hat.shape)
print(y_hat)

打印如下：

下面进行标准化处理
标准化x’ = (x - μ)／σ

#下面代码根据情况选择注释一行

mean_x = np.mean(x, axis = 0) #18 * 9 
std_x = np.std(x, axis = 0) #18 * 9 
for i in range(5652): #12 * 471
    for j in range(162): #18 * 9  未经过加权平均处理时使用
    #for j in range(18): #18  经过加权平均处理后使用
        if std_x[j] != 0:
            x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]
x

打印如下：

把x 和 y_hat 组合成一个矩阵，构成用于训练的数据集train_set，最后一列是pm2.5的真实数据，这一个操作用于方便后面的随机打乱操作

train_set = np.concatenate((x,y_hat),axis=1)
print(train_set.shape)
print(train_set[0:10,:])

打印如下：

下面就可以开始训练了。
使用adagrad

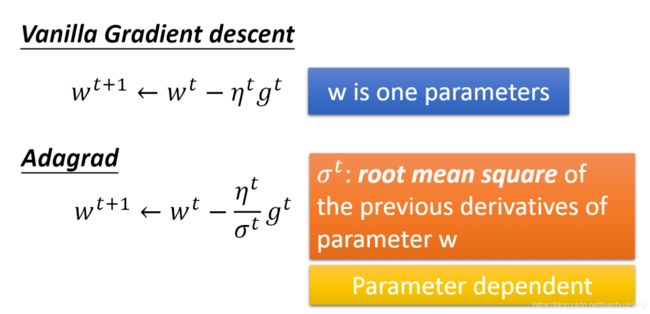
训练

下面的训练数据是没有经过加权平均处理的，一组特征数据是18*9=162维（我最后选用的是这个方法）
在训练之前，借用了深度学习里面的方法 epochs （不知道可不可靠）
5个epoch，每个epoch里面 iter_time = 10000，训练10000次，每个epoch之前，都对数据进行随机打乱，重新设置训练集和测试集

#按行随机打乱训练数据集
def shuffle(x):
    return np.random.permutation(x)

train_len = 5000
dim = 18 * 9 + 1 # w+b的维度
w = np.zeros([dim, 1])
learning_rate = 100
iter_time = 10000
adagrad = np.zeros([dim, 1])
eps = 0.01
epochs = 5

for epoch in range(epochs):

    train_set_shuffle = shuffle(train_set) #随机打乱
    train_set_x = train_set_shuffle[0:train_len,:-1]
    train_set_y = train_set_shuffle[0:train_len,-1]
    train_set_y = train_set_y.reshape((train_len,1))
    vali_set_x = train_set_shuffle[train_len:,:-1]
    vali_set_y = train_set_shuffle[train_len:,-1]
    vali_set_y = vali_set_y.reshape([5652-train_len,1])

    train_set_x = np.concatenate((train_set_x,np.ones([train_len,1])),axis=1)
    vali_set_x = np.concatenate((vali_set_x,np.ones([5652-train_len,1])),axis=1)

    for t in range(iter_time):    
        
        gradient = 2 * np.dot(train_set_x.transpose(), np.dot(train_set_x, w) - train_set_y) # 19*1
        adagrad += gradient ** 2
        w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
        if(t%1000==0):
            loss = np.sqrt(np.sum(np.power(np.dot(train_set_x, w) - train_set_y, 2))/train_len) #均方误差
            loss_vali = np.sqrt(np.sum(np.power(np.dot(vali_set_x, w) - vali_set_y, 2))/(5652-train_len)) #均方误差
            print(str(epoch)+"/"+str(epochs)+" "+str(t)+"/"+str(iter_time)+" "+"训练误差:" + str(loss))
            print(str(epoch)+"/"+str(epochs)+" "+str(t)+"/"+str(iter_time)+" "+"测试误差:" + str(loss_vali))
            print(str(epoch)+"/"+str(epochs)+" "+str(t)+"/"+str(iter_time)+" "+"第一个梯度大小:" + str(gradient[0]))
np.save('weight.npy', w)
w

下面的训练数据是有经过加权平均处理的，一组特征数据是18维（最后没有采用这个方法）

#按行随机打乱训练数据集
def shuffle(x):
    return np.random.permutation(x)

train_len = 5000
dim = 18 + 1 # w+b的维度
w = np.zeros([dim, 1])
learning_rate = 100
iter_time = 10000
adagrad = np.zeros([dim, 1])
eps = 0.01
epochs = 5

for epoch in range(epochs):

    train_set_shuffle = shuffle(train_set) #随机打乱
    train_set_x = train_set_shuffle[0:train_len,:-1]
    train_set_y = train_set_shuffle[0:train_len,-1]
    train_set_y = train_set_y.reshape((train_len,1))
    vali_set_x = train_set_shuffle[train_len:,:-1]
    vali_set_y = train_set_shuffle[train_len:,-1]
    vali_set_y = vali_set_y.reshape([5652-train_len,1])

    train_set_x = np.concatenate((train_set_x,np.ones([train_len,1])),axis=1)
    vali_set_x = np.concatenate((vali_set_x,np.ones([5652-train_len,1])),axis=1)

    for t in range(iter_time):    
        
        gradient = 2 * np.dot(train_set_x.transpose(), np.dot(train_set_x, w) - train_set_y) # 19*1
        adagrad += gradient ** 2
        w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
        if(t%1000==0):
            loss = np.sqrt(np.sum(np.power(np.dot(train_set_x, w) - train_set_y, 2))/train_len) #均方误差
            loss_vali = np.sqrt(np.sum(np.power(np.dot(vali_set_x, w) - vali_set_y, 2))/(5652-train_len)) #均方误差
            print(str(epoch)+"/"+str(epochs)+" "+str(t)+"/"+str(iter_time)+" "+"训练误差:" + str(loss))
            print(str(epoch)+"/"+str(epochs)+" "+str(t)+"/"+str(iter_time)+" "+"测试误差:" + str(loss_vali))
            print(str(epoch)+"/"+str(epochs)+" "+str(t)+"/"+str(iter_time)+" "+"第一个梯度大小:" + str(gradient[0]))
np.save('weight.npy', w)
w

误差比未经过加权处理的方法的误差大

预测

test_df = pandas.read_csv(test_path,encoding = 'big5',header=None
test_df = test_df.replace("NR",0.0)
test_df = test_df.iloc[:,2:]
test_df.head()

数据如下：

对数据进行处理：

t_data = test_df.to_numpy(dtype = float)
print(t_data.shape)
x_test = np.zeros([240, 18*9], dtype = float)
x_temp = np.zeros([18,9], dtype = float)
b = np.zeros([1,162],dtype = float)
for d in range(240):
    x_temp = t_data[d*18:(d+1)*18]
    b = x_temp.flatten()
    x_test[d] = b
print(x_test.shape)

mean_x_ = np.mean(x_test, axis = 0) #18 * 9 
std_x_ = np.std(x_test, axis = 0) #18 * 9 
for i in range(240):
    for j in range(162):
        if std_x_[j] != 0:
            x_test[i][j] = (x_test[i][j] - mean_x_[j]) / std_x_[j] #标准化

x_test = np.concatenate((x_test,np.ones([240, 1])),axis = 1).astype(float)
print(x_test.shape)
print(x_test)

打印如下：

w = np.load('weight.npy')
y = np.dot(x_test, w).astype(int) #预测值取整
print(y.shape)
y

保存预测值

import csv
with open('submit.csv', mode='w', newline='') as submit_file:
    csv_writer = csv.writer(submit_file)
    header = ['id', 'value']
    print(header)
    csv_writer.writerow(header)
    for i in range(240):
        row = ['id_' + str(i), y[i][0]]
        csv_writer.writerow(row)
        print(row)

总结

数据处理时，用标准化x’ = (x - μ)／σ比用归一化（Min-Max Normalization） x’ = (x - X_min) / (X_max - X_min)要好一点，我已开始用的Min-Max Normalization，很难训练，具体原因网上有很多说法，没去深究。

用加权平均对数据进行处理后，训练误差与测试误差变大了，可能是因为平均化处理抹掉了一些特征信息，毕竟加权处理后，一组特征数据用原来的18*9维掉到了18维。