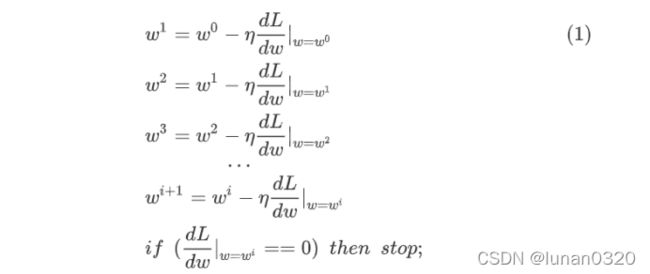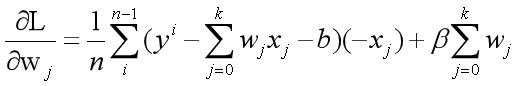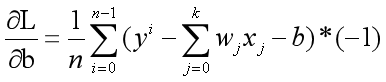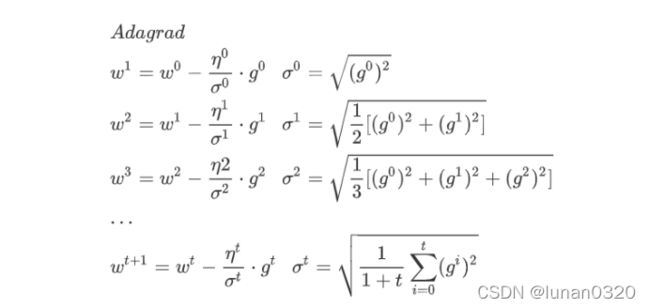机器学习实验一（李宏毅-预测PM2.5）

机器学习 Lab1 实验报告

欢迎大家访问我的GitHub博客

https://lunan0320.github.io/

一、实验目的

掌握Linear Regression中梯度下降预测模型，根据空气质量监测网下载的观测数据，预测出空气污染指数(即PM2.5) 的数值。

二、实验要求及环境

2.1 实验要求

1、不可以使用numpy.linalg.lstsq
2、可以使用pandas库读取csv文件数据信息(其他库亦可)
3、必须使用线性回归，方法必须使用梯度下降法
4、可以使用多种高阶的梯度下降技术（如 Adam、Adagrad等
5、程序运行时间不得大于3分钟

2.2实验环境

戴尔G3游匣 Intel core i7 Windows10
Python3.8 PyCharm

三、设计思想

3.1 实验思想

train.csv：（24018）24即432024的表格，每一天有18个特征，共12个月，每个月20天的数据。
test.csv: (24018)9即43209的表格，每一天有18个特征，需要预测的是每一天第10小时的PM2.5，并输出到csv文件中。

3.1参数更新

3.2 偏微分计算

3.3 Loss function

3.4 Adagrad过程

3.2模型构想

3.2.1 模型一：只考虑PM2.5这一个特征。

3.2.2 模型二：考虑5个影响PM2.5较大的特征。

3.2.3 模型三：考虑全部18个特征。

四、模型一

每一天只考虑PM2.5这一个特征
代码及数据见文件：1.0_predict.py 1.0_predict.csv

4.1数据读取及预处理

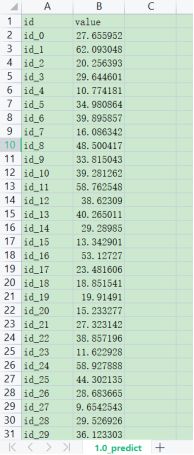
   train.csv文件中，需要提取3-27列的内容，其中RAINFALL行的内容‘NR’替换为数值0包是没有降雨，数值小于0的数替换为0，并将数据表转化为二维数组处理。

  考虑将每一天分为15组（没有将每一天的数据连起来），每一组是一个189的数组，即0-8，1-9…14-22。此时共15240=3600的189的数组表。
   那么此时的x应该是一个三维数组3600189，第一维度表示的是第几个189的数组表，第二维度表示189表格的第几行，第三维度表示189表格的第几列。y是一个3600个元素的列表，一一对应x每个表格应有的y值。

4.2梯度下降迭代过程

4.2.1 Gradient Descent以及训练集分割

  每一次迭代都需要调用梯度下降算法，求出此时的梯度grad_w和grad_b。

  需要遍历3600个18*9的表格，对每个表格根据loss_function的定义，对b和w求偏导。此处，将w视为向量数组，需要用到numpy中求向量积的方法np.dot()

此时的训练集为3000个18*9的表格，其余600个作为验证集。

4.2.2 Regularization正则化（可不做）

  为了使得训练出的数据能够在test上更好的预测，此处采用正则化技术。但是由于正则化技术是针对高次项带来的误差所引起，引入正则项也是为了消除高次项的影响，因此在这里引入正则化方法，意义不大。

4.2.3 Adagrad梯度更新

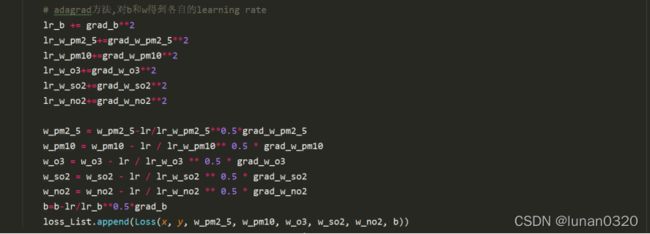
  为了能够在较短时间内尽快收敛，因此考虑采用高阶梯度收敛方法，对每个w以及b求出各自的learning rate，将不同参数的learning rate分开考虑。

  区别于普通的Gradient Descent方法，当梯度值即微分值越大的时候、斜率越大的时候，更新的步伐要更大一些， 在Adagrad的表达式中，分母表示梯度越大步伐越小，分子表示梯度越大步伐越大，这样二者可以相互约束，变化幅度比较合理。

  据此，对于每次迭代过程中求得的梯度grad_w,grad_b均需要求平方并与各自的learning rate求和求得均方根，与初始化的Learning rate共同组成各自的learning rate，继而根据梯度下降的策略求出更新后的w和b。

4.2.4 对Validation Data计算Loss

  Loss值的计算是根据原值与预测值的差值平方来估计的。
此处按照训练集3000，验证集600的比例即5:1划分。

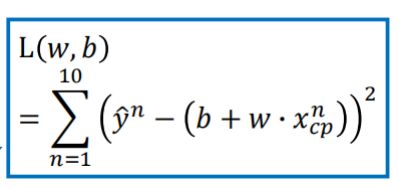
4.3 对test.csv数据处理并预测

  同样需要读取的是test.csv文件中的2-11行数据，对数据’NR’项预处理，对数据小于0的项替换为0。
  读出每一天的PM2.5对应的行即可。

  得到test数据后，用梯度下降求得的w和b去预测test数据对应的PM2.5，并做出图像。

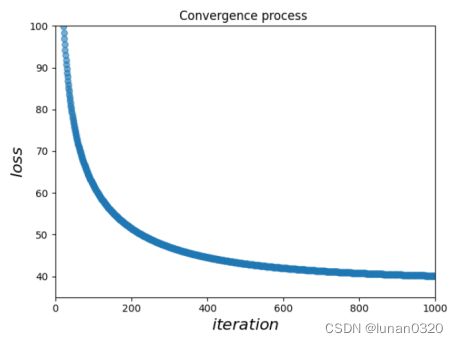
  可以看到，随着训练次数的增多，学习后的数据在验证集上的loss值越来越小，最终趋于稳定，将结果输出到了1.0_predict.csv文件中。

  最终在验证集上的loss值也稳定在了40.12左右，训练的时间为72.7秒。

五、模型二

  在每一天只选取几个影响PM2.5较大的特征。
代码及数据见文件：2.0_predict.py 2.0_predict.csv

  查阅资料后发现，世界卫生组织[1]对空气质量和健康发布的一篇文章显示：影响PM2.5大小的主要因素就是几个。

  因此，在模型二中考虑的是主要影响因素。综合考虑So2、No2、PM2.5、PM10、O3五种因素
y=b+(w1x1+w2x2+…+w9x9)_PM2.5 第9行
+(w1x1+w2x2+…+w9x9)_PM10 第8行
+(w1x1+w2x2+…+w9x9)_O3 第7行
+(w1x1+w2x2+…+w9x9)_So2 第12行
+(w1x1+w2x2+…+w9*x9)_No2 第5行

5.1 均匀选择Validation Data

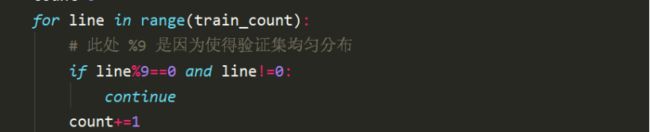
  在模型一中，验证集的选择是直接选取了18*9的数组的最后600个作为验证集，而不是在3600个数组中均匀选择，这必然会带来一定的误差影响。因此，在模型二中对验证集均匀分割，每9个之后将一个数据加入验证集。
  训练集：3200，验证集：400即8：1的比例训练与loss验证。

5.2 Adagrade梯度下降

  为了能够有更好的收敛性，与模型一相同，采取的是Adagrade的梯度下降方法。
  除了参数较多之外，其余部分与模型一基本相同。

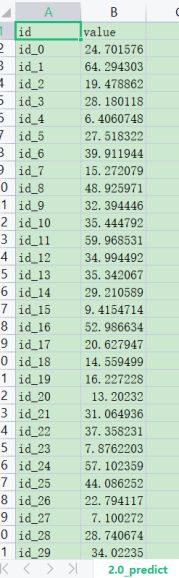
5.3对test.csv数据处理并预测

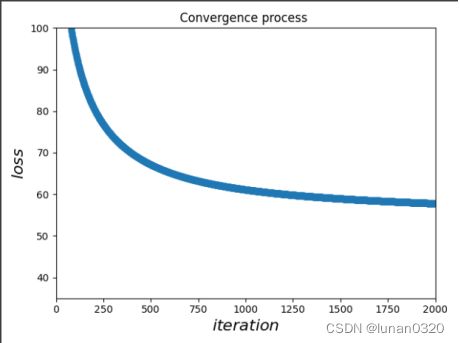
  可以看到，随着训练次数的增多，模型趋于稳定，在验证集上的loss值逐渐减小。

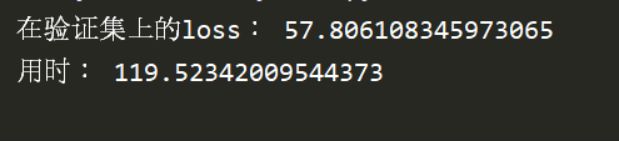
  从训练结果可以看出，当训练2000次后，在验证集上的loss值趋于57.8，在仅仅训练2000次情况下，时间竟然已经达到了2分钟左右。

六、模型一、二优化

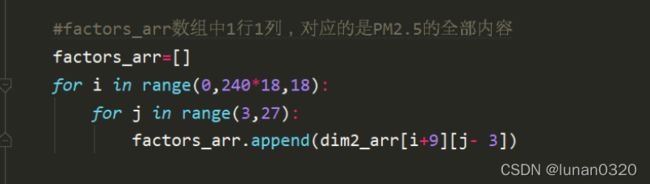
6.1 Feature单独提取

  将train.csv文件中的全部的PM2.5数据统一放入一个一维数组中。

6.2矩阵运算

  在模型一、二中有个共同的问题是迭代次数受限制，当迭代次数达到2000以上时，训练时间就会急剧上升，从而超过实验要求的三分钟限制。因此，需要对模型做出改进，使用numpy自带的数组矩阵运算做效果会更好。

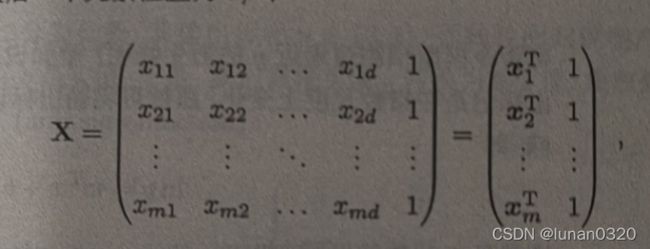
  查阅资料后发现，对于bias而言，可以构造X的0次项，如此，便不需要单独考虑bias，只需考虑w的vector即可，构造如图所示的X矩阵即是训练数据。

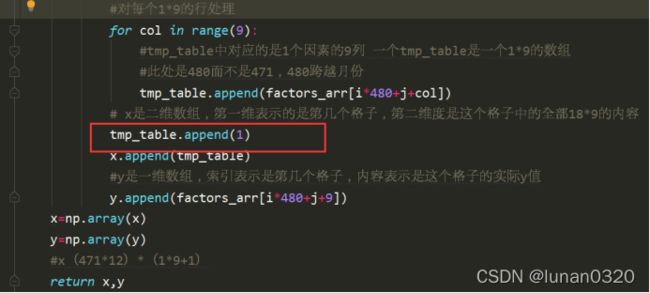
  继而在梯度下降的过程中，不需要单独考虑某个因素的影响，只需要综合考虑即可，迭代过程也变的更加清晰。

6.3 Adagrad效率优化

  将向量之间的运算转换到矩阵运算之后，在传参以及计算的过程中效率会成倍的提升。

  需要注意的是，在求偏导的过程中，为了完成矩阵之间的相乘，需要对X矩阵先做一个转置变化，这在numpy中是很容易的操作。
  求平方根的过程也通过np.sqrt()函数显得非常快捷。

6.4 每天数据扩充统一

  在模型一、二中并没有把天与天之间的数据联系起来，是以天为单位训练，这对数据的最大化利用是不利的。因为每个月的数据是连续的，因此可以考虑将每个月的数据综合考虑。
  每个月20天，共2024=480h，但是最后9h是无法利用的，因此每个月可以组合出的189的数组共计480-9=471组。
  此时x是（12471）（189+1）即5652163的二维数组（加1是为了转换为矩阵，将bias的影响纳入）

6.5 模型一优化后

6.5.1Gradient Descent

  对于最普通的梯度下降算法而言，设置learning rate为0.0000001，iteration为80000次
在最普通的梯度下降算法之下，得到的loss值在42.7左右,但是用时却大大缩短，只需20秒即可完成80000次的迭代。

6.5.2Adagrad算法

  根据题目要求，需要测试四组不同learning rate情况下的loss曲线。
  图中w=np.ones(1*9+1)是指共9个w参数，+1是最后一个用来表示bias的值，将bias在w的最后一个表示。

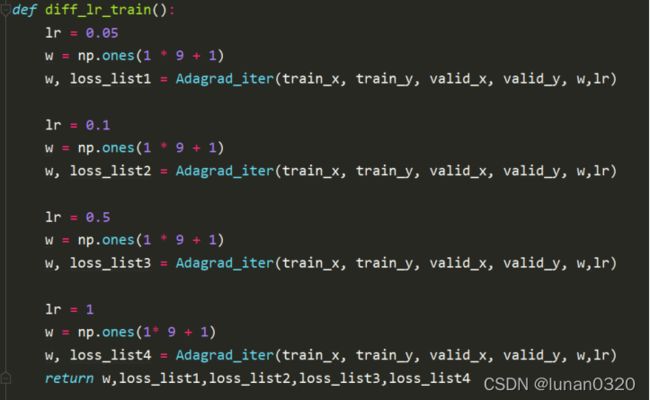
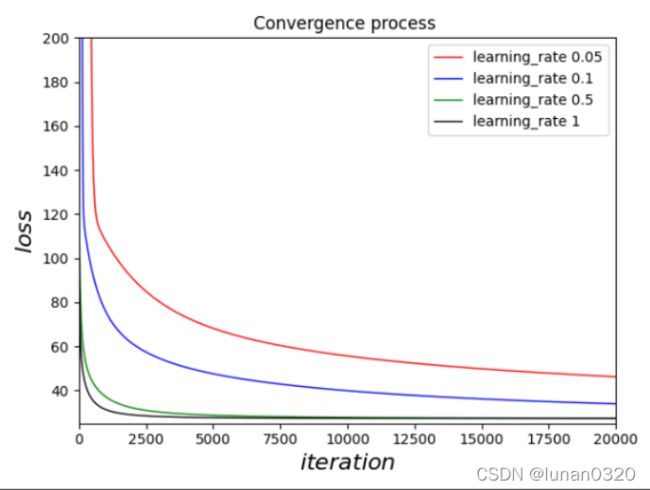
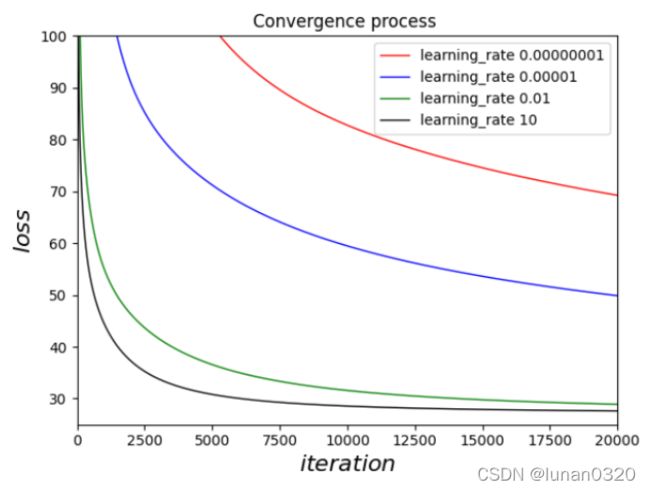
  在不同的学习率下，分别测试各种情况下的loss值，并最终通过plot作图，得到四种learning rate下随着迭代次数的增多，loss的变化曲线。

  可以看到，随着learning rate的增大，loss值的收敛过程是越来越快的，在Adagrad梯度下降算法下，这是符合的。
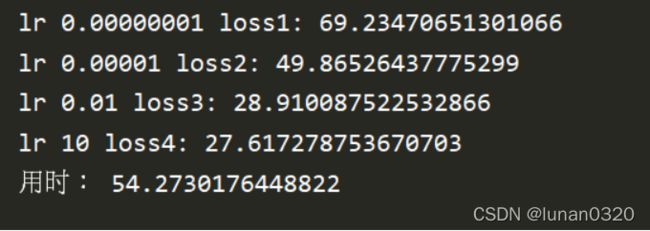
  四种不同的learning rate对应的在最终w情况下的loss值：

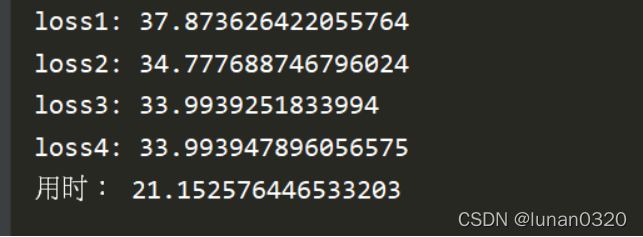
6.6 模型二优化后

  此时特征提取后对应的factors_arr数组是5行1列的二维数组，对应的5行依次是No2、O3、PM10、PM2.5、So2

Adagrad算法
  分别在四种不同learning rate之下，求得验证集下不同的loss值。作图比较发现，随着learning rate的增大，梯度下降算法的收敛过程是越来越快的。

  可以看到在迭代20000次是情况下，loss值在验证集下已经趋近于27.32。
  在4中不同学习率情况下，每次迭代20000次，共计80000次，用时大概44秒，相当于依次迭代20000次用时11秒左右。在没有优化之前，迭代2000次需要120秒，比较下来，时间提升了109倍。优化效果是非常显著的。

七、模型三

  在模型三中需要考虑18种特征的影响。对于一个189的最小单元，共有w和b 189+1=163个参数的影响。

7.1 Feature Scaling归一化处理

  在如此多的特征面前，各个特征的分布范围是不同的，此时不同的特征值变化相同的幅度带来的影响是会有较大差别的，为了消除这种差异性，使得update的过程更为顺利，需要对数据进行归一化处理。

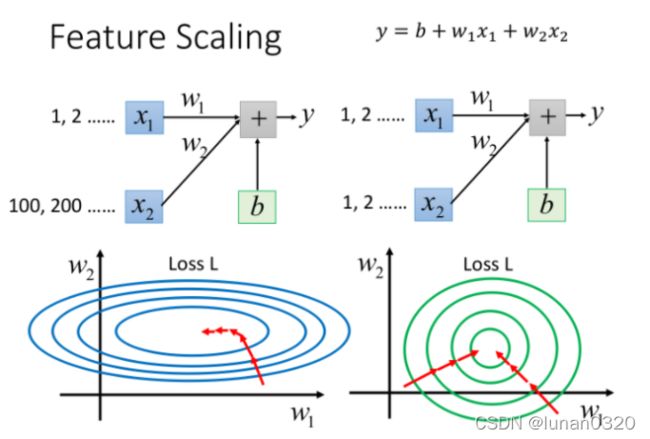
  归一化处理之后，loss的图像接近于圆形，整体上都会顺着等高线的方向趋向于圆心移动，提高训练的效率。
  此处使用的Feature Scaling方法是对每个特征归一化为标准正态分布，即每个Feature减去它的均值再除以标准差即可。

  在具体的实现过程种需要使用numpy的mean和std方法。

  factors_arr数组是18*5652的数组，每一行是一个特征的所有取值，因此直接对其按行求均值和方差即可。
最后还需要利用Feature Scaling公式更新每一个数据。

7.2 优化Validation Data选取

  验证集不能够随意分布，而是应该均匀分布在12*471=5652之内，因此可以选择12为验证集的间隔。

7.3 Stochastic Gradient Descents随机梯度下降

  为了让训练更加快速，考虑引入SGD随机梯度下降算法，看到一个样本点就去更新loss，此时，loss就不是所有样本的平方和，而是随机样本点的平方和。

  该方法与Adagrad的最大不同就是红色框的部分，随机梯度下降算法并没有像Adagrad迭代所有数据，只是随机取一个样本点求其平方和。
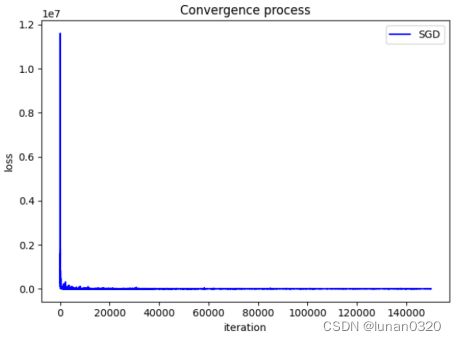
  在选择learning rate0.01，迭代次数150000时，得到的loss值为80.5左右。当选取的学习率较小，或者迭代次数较少时，得出的训练loss值都是非常大的。

  对迭代次数20000和150000分别作图观察，可以看到这需要非常高的迭代次数才可以收敛到理想值，因此这不是我在本次梯度下降模型中选取的算法。

7.4 Adagrad算法

  采用Adagrad算法是与模型二类似的，区别只是选取的特征数量的不同。

  得到在四种不同的learning rate下的loss值。每次迭代20000次，分为4组，共用时53秒左右，效率的提升非常显著。
  在learning rate为1的情况下，求出的loss值是27.62左右，这与只考虑5个特征的情况是差不多的。
  这也成功验证了我起初的猜想，在主要影响因素面前，其他的13个特征造成的改变基本上可以忽略不计。

在四种learning rate下，作图比较，可以看到，大致趋势与之前是相同的。

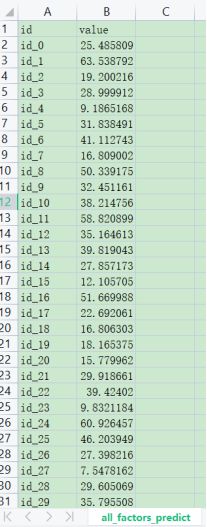
为了直观地看出最后预测模型的情况，作出了最终预测结果PM2.5的折线图。

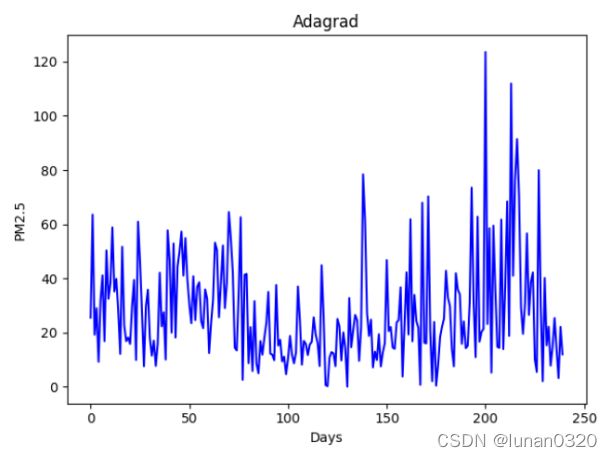
  此时为了对模型三更好评估，继续测试不同learning rate下的loss曲线。
按照learning rate每次扩大1000倍，迭代20000次。训练用时54秒。

按照learning rate每次扩大1000倍，迭代50000次。训练时间为142秒。
  对比之下，可以看到，此时的主要影响因素已经不再是训练次数所影响， 即使扩大5倍的训练量，此时的loss值也是变化很小的，已经达到了趋于收敛的状态。

八、模型评价

8.1优点

8.1.1、模型特征由一而多

  从一个特征到主要特征再到全部特征，分为三次建模，两次优化，得到了线性回归模型下的最优解。

8.1.2、矩阵运算效率大幅度提升

  为了消除时间瓶颈的影响，查阅资料后获得思路，转换为矩阵做时间提升达到了109倍。

8.1.3、使用多种高阶回归方法

  在优化模型的过程中，使用了Adagrad作为主要优化方法，SGD辅助对比。

8.1.4、Feature Scaling归一化

  使用归一化技术，使得消除了不同特征之间的影响，更容易收敛到最佳情况。

8.1.5、验证集均匀分布

  将训练集和验证集分割，而验证集又是充分随机选取，使得模型更容易推广，从而降低了test数据下的误差。

8.2缺点

8.2.1、预处理小于0直接替换为0

  对于数据中出现小于0的数值，直接替换为0欠妥，这会导致一些不确定因素加入。最合适的做法应当是将其从数据集中筛除。

8.2.2、验证集Validation没有完全随机

  训练集的随机性是建立在固定的随机方式上，本质上没有做到完全随机均匀分布，且Validation Data与Training Data的分割可以更加均匀合理。

8.2.3、影响大小应随距预测时间远近而动态变化

  未对各个小时的影响做淡化处理，随着时间的递增，组内第九小时、第八小时…第一小时对于待预测时刻的影响应该是递减的。也就是说距离待预测时刻越近，影响因素的影响会更大。

8.2.4、Adagrad优化瓶颈

  虽然通过Adagrad方法使得不同的变量有了各自的学习率，但是初始情况的全局学习率需要自己指定。
  此时，如果设置的全局学习率过大，则优化一样是不稳定的；
  如果设置的全局学习率过小，则随着迭代过程的进行，根据Adagrad的学习特性，学习率可能会越来越小，很有可能在没有到达极值点的时候就已经是停滞不前的状态了。

九、结论

  考虑不同的特征值会有不同的结果，但是在选择模型的时候如果可以优先挑选主要特征，这比直接选取全部特征来进行要更加有效。
  即使选取了所有特征值，在最终也需要对那些影响微乎其微的特征舍弃。
  不同的高阶梯度下降优化方法不一定总是适用的，如果迭代时间较长，那么Adagrad就存在明显的劣势，不容易在较短时间内找到最优解，SGD方法是的计算速度是要比Adagrad快一个数量级的。
  Training Data和Validation Data要区分开，不能在训练集中直接选取一部分用来验证求loss值的大小。Training Data中用来训练模型，而Validation Data用来验证模型优劣，计算loss值。

十、参考文献

[1]世卫组织 环境（室外）空气质量和健康
https://www.who.int/zh/news-room/fact-sheets/detail/ambient-(outdoor)-air-quality-and-health
[2]哈工大2020秋机器学习Lab1实验报告
https://blog.csdn.net/weixin_44940258/article/details/109010846
[3] 数组对象
https://www.numpy.org.cn/reference/arrays/
[4] Data-Science-Notes
https://github.com/fengdu78/Data-Science-Notes/tree/master/2.numpy/numpy-100
[5] Pandas手册
https://www.pypandas.cn/docs/getting_started/basics.html
[6] Adagrad 优化
https://www.jiqizhixin.com/graph/technologies/7eab38a3-23ec-494c-a677-415b6f85e6c5

十一、提交文件注解

训练集：train.csv
预测集：test.csv
1、模型一：代码1.0_predict.py 数据1.0_predict.csv
2、模型一优化：代码1._factor.py 数据1._factor_predict.csv
3、模型二：代码2.0_predict.py 数据2.0_predict.csv
4、模型二优化：代码5_factors.py 数据5_factors_predict.csv
5、模型三：代码all_factors.py 数据all_factors_predict.csv