MATLAB编程练习题
例1、产生100到1的等差数列,数据点为20个,赋值给x。获取x的第10个单元的值,赋值给x1;获取x的前10个单元的值,赋值给x2;获取x的后5个单元的数据,赋值给x3;将x的偶数单元中的数据赋值给x4;将x的数据倒排序赋值给x5。
>> x = 100:-5:1; %产生100到1的等差数列,数据点为20个,赋值给x
x1 = x(10); %获取x的第10个单元的值,赋值给x1
x2 = x(1:10); %获取x的前10个单元的值,赋值给x2
x3 = x(16:end) %获取x的后5个单元的数据,赋值给x3
x4 = x(2:2:end) %将x的偶数单元中的数据赋值给x4
x5 = fliplr(x); %将x的数据倒排序赋值给x5
%运算结果
x =
100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5
x1 =
55
x2 =
100 95 90 85 80 75 70 65 60 55
x3 =
25 20 15 10 5
x4 =
95 85 75 65 55 45 35 25 15 5
x5 =
5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
2.创建矩阵A和B,然后执行下列运算:
Y1=A+B
Y1=A.+B
Y2=A-B
Y2=A.-B
Y3=AB
Y3=A.B
Y4=A\B
Y4=A.\B
Y5=A/B
Y5=A./B
Y6=A^2
Y6=A.^2
Y7=3^B
Y7=3.^B
Y8=A^B
Y8=A.^B
A = [1 2 3; 3 4 5; 2 6 12];
B = [-1 -4 6; 7 -3 10; 5 4 1];
Y1 = A+B;
% Y1 = A.+B ; %报错,无效运算符
Y2 = A-B;
% Y2 = A.-B ; %报错,无效运算符
Y3 = A*B;
Y3 = A.*B;
Y4 = A\B;
Y4 = A.\B;
Y5 = A/B;
Y5 = A./B;
Y6 = A^2;
Y6 = A.^2;
Y7 = 3^B;
Y7 = 3.^B;
% Y8 = A^B; %报错,无效运算符
Y8 = A.^B;
%运算结果
Y1 =
0 -2 9
10 1 15
7 10 13
Y2 =
2 6 -3
-4 7 -5
-3 2 11
Y3 =
28 2 29
50 -4 63
100 22 84
Y3 =
-1 -8 18
21 -12 50
10 24 12
Y4 =
17.5000 15.5000 -11.5000
-22.0000 -25.5000 23.0000
8.5000 10.5000 -9.5000
Y4 =
-1.0000 -2.0000 2.0000
2.3333 -0.7500 2.0000
2.5000 0.6667 0.0833
Y5 =
1.3333 -0.6357 1.3566
2.0000 -0.9302 2.3023
5.3333 -2.4961 4.9612
Y5 =
-1.0000 -0.5000 0.5000
0.4286 -1.3333 0.5000
0.4000 1.5000 12.0000
Y6 =
13 28 49
25 52 89
44 100 180
Y6 =
1 4 9
9 16 25
4 36 144
Y7 =
1.0e+03 *
0.1408 0.0190 0.1861
0.9539 0.1288 1.2615
0.8131 0.1098 1.0754
Y7 =
1.0e+04 *
0.0000 0.0000 0.0729
0.2187 0.0000 5.9049
0.0243 0.0081 0.0003
Y8 =
1.0e+06 *
0.0000 0.0000 0.0007
0.0022 0.0000 9.7656
0.0000 0.0013 0.0000
例3、生成相量A,其元素为区间[1, 999]内的整数,然后找出A中能被13整除且大于500的数。
A = 1:999;
n = 1;
for i=1:999
if A(i)>500 %先找到大于500的数
if rem(A(i),13)==0 % r=rem(a,b) 返回a除以b后的余数,其中a是被除数,b是除数。此函数通常称为求余运算,表达式为r=a-b.*fix(a./b)。rem函数遵从rem(a,0)是NaN的约定。
b(n) = A(i) %将找到的数存储在数组b中
n = n+1;
end
end
4.求线性方程组的系数矩阵的行列式、迹、秩、逆,并求解线性方程组。
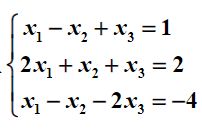
A=[1 -1 1;2 1 1;1 -1 -2];
b = [1;2;-4]; %
c1 = det(A); %系数矩阵的行列式
c2 = trace(A); %系数矩阵的行列式的迹
c3 = rank(A); %系数矩阵的行列式的秩
c4 = inv(A); %系数矩阵的行列式的逆
c5 = c4*b; %解向量
c1 =
-9
c2 =
0
c3 =
3
c4 =
0.1111 0.3333 0.2222
-0.5556 0.3333 -0.1111
0.3333 0 -0.3333
c5 =
-0.1111
0.5556
1.6667
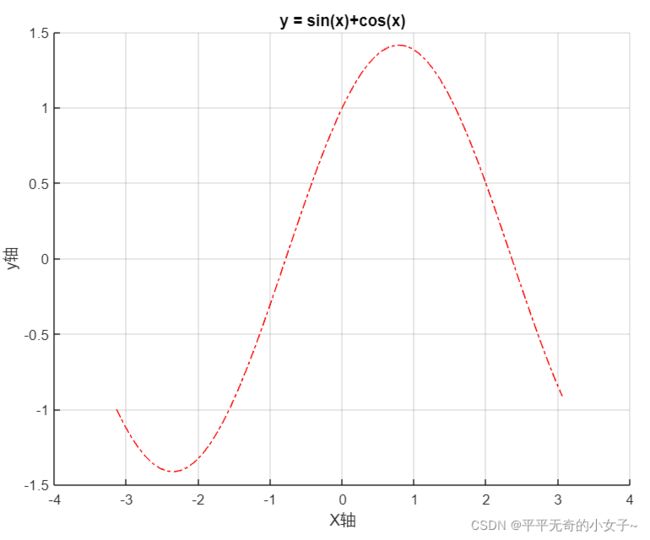
例5、用红色点画线方式绘制函数y = sin(x)+ cos(x)在[-π,π] 上的曲线,并以“函数”为标题。
x = -pi:0.1:pi;
y = sin(x)+cos(x);
plot(x,y,'r-.');
grid on;
box off;
xlabel('X轴');
ylabel('y轴');
title('y = sin(x)+cos(x)');
例6、用多子图方式分别绘制曲线y1= sin(x+1), y2=e^(0.5x),y3= y1+y2在[0,5π]上的曲线。
x = 0:0.1:5*pi;
y1 = sin(x+1);
y2 = exp(0.5*x);
y3 = y1+y2;
subplot(3,1,1); %子图1
plot(y1);
title('y1 = sin(x+1)')
subplot(3,1,2); %子图2
plot(y2,'r-.');
title('y2 = exp(0.5*x)')
subplot(3,1,3); %子图3
plot(y3,'b*');
title('y3 = y1+y2')
例7、采用多图叠绘的方式分别绘制正弦曲线y1=sin(x+1)、 余弦曲线y2= cos(x)+ 1在区间[0,2π] 上的曲线,要求两条曲线,一条用实线,一条用虚线,一条用红色,一条用绿色,线宽均设置为2,并为两条曲线添加图例“正弦曲线”和“余弦曲线”。
x = 0:0.01:2*pi;
y1 = sin(x+1);
y2 = cos(x)+1;
plot(x,y1,'r',x,y2,'g:',LineWidth=2);
legend('正弦函数','余弦函数'); %添加图例
例8、绘制三维曲线x= 3tsint ,y=3tcost,Z=t,t∈[1,10]。
t = 1:0.01:10;
x = 3.*t.*sin(t);
y = 3.*t.*cos(t);
z = t;
plot3(x,y,z,'r');
title('三维曲线');
grid on;

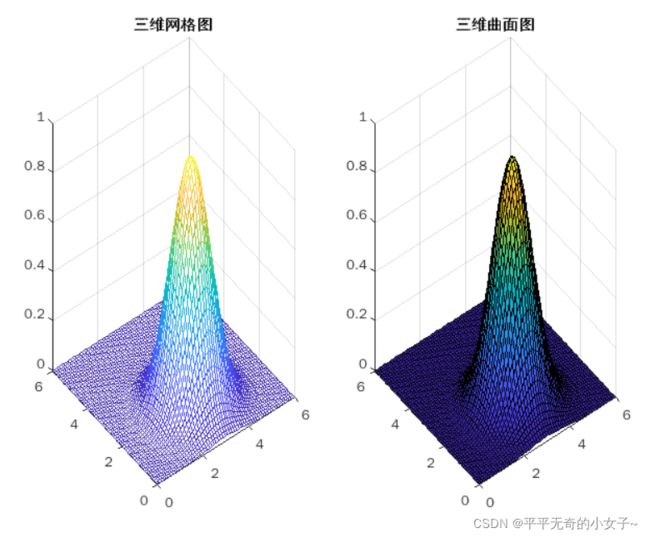
例9、在 XY 平面内选择区域[0,6]和[0,6]绘制二维高斯函数的三维网格曲面。

t = 0:0.1:6;
[x,y] = meshgrid(t); %网格数据的生成
z = exp(-((x-3).^2+(y-2).^2));
subplot(1,2,1)
mesh(x,y,z); %三维网格图
title('三维网格图');
subplot(1,2,2)
surf(x,y,z); %三维曲面图
title('三维曲面图');
例10、在 XY 平面内选择区域[-6,6]和[-6,6]绘制函数的三维曲面。
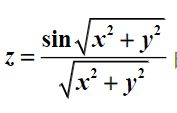
t = -6:0.1:6;
[x,y] = meshgrid(t); %网格数据的生成
z = sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2);
subplot(1,2,1)
mesh(x,y,z); %三维网格图
title('三维网格图');
subplot(1,2,2)
surf(x,y,z); %三维曲面图
title('三维曲面图');

例11、利用 while 循环求出 100 到 200 之间第二个能被 31 整除的数。
x = 100:200;
i = 1;
n = 0;
while n<2
if rem(x(i),31)==0
n = n+1;
y(n) = x(i);
end
i=i+1;
end
disp(y(2))
%显示结果
155
sum = 0;
for i=0:1000000
sum = sum+0.2^i;
end
disp(sum)
%结果
sum =
1.25