[1] A Keypoint-based Global Association Network for Lane Detection
A Keypoint-based Global Association Network for Lane Detection
0. 摘要
概括车道线检测方法:
(1)基于Anchor定位的方法,自顶向下根据路线图把预设定的Anchor回归到车道线上。缺点是对复杂车道线不够灵活;
(2)基于keypoint estimate的方法,自底向上给检测到的车道线关键点分组,同组构成一条车道线。缺点是低效且耗时。
本文提出的方法GANet,配以LFA,从局部和全局两个角度对keypoint进行回归以检测车道线。
1. 介绍
车道线检测对自动驾驶和构建高精地图具有重要的意义。
基于Anchor的车道线检测方法受目标检测的启发,许多工作遵从自顶向下的方法来检测车道线。一系列方向各异的直线作为anchor,然后通过计算位移,把anchor回归到直线上的点。最后使用NMS来选择置信度比较高的直线。这种方法的局限在于预先设定的直线anchor对各种形状的线的泛化能力较弱,灵活性较差
基于keypoint estimate的方法,自底向上检测车道线,可以更灵活地检测各种形状的车道线。求得线的稀疏表达,通过估计空间关系来联系相邻的关键点,迭代地把属于同一条线的关键点连接起来。这种方法适合形状各异的车道线,但是效率较低且十分耗时。局部的连接由于缺乏全局的视野,会导致错误,累计错误则会导致车道线检测失败。
本文提出GANet,从全局和局部两个互补角度来解决上述问题。每条线用一个start point表示,其他关键点通过与start point计算位移偏差,来确定其所属的start point,同属一个start point邻域的所有keypoint属于同一条车道线实例。此过程中所有keypoint的计算相互独立,可以同时进行。全局匹配相比于逐点累积匹配更鲁棒。
确定相邻点的前后顺序,LFA模块用于整合局部关键点。采用2D可变形卷积预测邻接点的位移偏差。添加辅助的损失函数来辅助估计每个点的偏差
贡献点:
(1)提出基于全局关键点回归的车道线检测方法GANet
(2)提出局部特征整合模块LFA,用于校正相邻关键点
(3)SOAT
2. 相关工作
2.1车道线检测方法
车道线检测任务目标是获取车道线的形状并加以区分,主要分为以下几类:
基于分割的方法 基于分割的方法采用对每个像素进行车道线和背景二分类的模型。为了区分不同的车道线,SCNN把不同的车道线视为不同的类别,把车道线检测问题转换为多类分割问题。切片CNN结构用于在行列之间传递信息。为了达到实时,ENet-SAD采用自注意力蒸馏机制来整合上下文信息,从而可以使用小backbone。LaneNet采用实例分割的思路,二值分割与特征嵌入同时用来区分车道线实例。本文使用偏移量而不是嵌入特征来聚类每条车道线,更高效。
基于检测的方法 这类方法通常遵循自顶向下top-down的方法来预测车道线。基于锚点的方法设计类线的锚点,在采样点和预设锚点之间回归偏移量。NMS来选择置信度高的车道线。LineCNN采用从图像边缘出发的具有特定方向的射线来采样一组锚点。Curve-NAS在垂线上定义锚点,然后使用NAS搜索更优的backbone。LaneATT提出了基于anchor的池化方法,并且使用注意力机制来整合更多的全局信息。还有其他方法把车道线检测视为行级分类问题,对于每一行,模型预测可能含有车道线的位置。
基于关键点的方法 受人体关键点检测方法的启发,一些工作把车道线检测看作关键点的估计和连接问题。PINet使用沙漏网络预测关键点的位置和嵌入特征,使用嵌入特征来聚类不同的车道线。FOLOLane预测像素级同分辨率热点图来获取车道线上的点,使用局部线型构建方法来连接关键点,生成整条车道线。本文的GANet采用了更高效的后处理方法,不需要嵌入特征或者局部特征点关联机制来构建整条车道线。每个点并行地使用其到开始点的偏移量来找到所属的车道线。
2.2
传统CNN因为采用固定的网格状采样范围,对不规则结构的建模能有限。可变形卷积可以自适应地整合局部信息,来解决这个问题。和标准卷积相比,2D偏移量可以通过其他卷积得到,以实现采样网格的自由变形。通过学到的偏移,卷积的感受野和采样位置可以根据目标随机的形状和尺寸进行自适应调整。可变形卷积广泛应用于目标检测、目标跟踪和视频理解。RepPoints把目标建模为一系列的点,并使用可变形卷积预测这些点到目标中心的位移。这个可变形的目标表征方法为目标检测和语义特征抓取提供了精确的几何位置。Ying等提出3D可变形卷积来探索时-空信息,并在视频超分上实现自适应运动理解。与这些方法不同的是,本文提出的LFA适用于车道线这种长结构,并通过车道限级别的可变形卷积把范围特征约束到每条线的邻接点上。
3. GANet
![[1] A Keypoint-based Global Association Network for Lane Detection_第1张图片](http://img.e-com-net.com/image/info8/549c13d3b75c4049be6243bfdef61379.jpg)
GANet结构如上图。车前图像作为输入,FPN+backbone用于提取特征。SA为自注意力模块,用于丰富上下文信息。解码阶段,关键点预测头和位移预测头生成关键点置信度图和唯一图。两个预测头由全卷积构成。LFA模块用在关键点预测头之前,用于增强邻接关键点的局部联系,从而更容易生成连续的车道线。对于每条车道先实例,首先在位移图中选择值小于1的点作为车道线始点,即聚类中心点。然后,属于同一条车道先的关键点根据置信度图和位移图聚成一类,生成1条车道线。
3.1 全局关键点关联
3.1.1 关键点估计
对于输入图像 I ( H ∗ W ∗ C ) I(H*W*C) I(H∗W∗C),GANet预测线集合 L = { l 1 , l 2 , . . . , l N } L=\{l_1,l_2,...,l_N\} L={l1,l2,...,lN},每条线由 K K K个关键点表示, l i = { p i 1 , p i 2 , . . . , p i K } l_i=\{p_i^1,p_i^2,...,p_i^K\} li={pi1,pi2,...,piK} 。每个关键点由像素位置表示 p i j = ( x i j , y i j ) p_i^j=(x_i^j, y_i^j) pij=(xij,yij)。为了估计关键点的位置,使用置信度预测头输出置信度图 Y ^ ( H r ∗ W r ) \hat{Y}(\frac{H}{r} * \frac{W}{r}) Y^(rH∗rW)。置信度图表示每个位置存在关键点的置信度。置信度图GT的生成过程:在标注的车道线上采样 K K K个关键点,然后把关键点投到空白的 Y ^ \hat{Y} Y^,然后使用高斯函数生成该点及其周围的置信度。重叠区域按像素取最大值。
使用惩罚递减的focal loss(penalty-reduced focal loss)来平衡关键点区域和非关键点区域的不均衡问题。
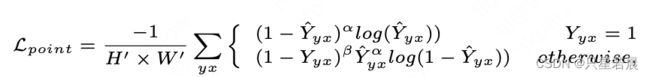
为了解决图像卷积过程中下采样导致的位置变换造成的性能损失(位置需要向下取整),添加位置补偿图 δ x y = ( x j j r − ⌊ x j j r ⌋ , y j j r − ⌊ y j j r ⌋ ) \delta_{xy}=(\frac{x_j^j}{r}-\lfloor\frac{x_j^j}{r}\rfloor,\frac{y_j^j}{r}-\lfloor\frac{y_j^j}{r}\rfloor) δxy=(rxjj−⌊rxjj⌋,ryjj−⌊ryjj⌋),使用L1 Loss。
![[1] A Keypoint-based Global Association Network for Lane Detection_第2张图片](http://img.e-com-net.com/image/info8/5c06dd6efb17454c8e16f72f4b1140af.jpg)
3.1.2 始点回归
为了区分不同的车道线。使用始点代表每条车道线实例,因为始点比较稳定并且始点之间具有明显的位置差异。本文回归每个点到试点的位移,而不是直接回归始点的位置。每个点到始点的位置表示如下:

因此,可以生成位移图 Q y x ( H r ∗ W r ∗ C ) Q_{yx}(\frac{H}{r}*\frac{W}{r}*C) Qyx(rH∗rW∗C)。关键点 ( x i j , y i j ) (x_i^j,y_i^j) (xij,yij)处的值为该点到始点的位移,非关键点处值为0。 C = 2 C=2 C=2分别表示在x方向和y方向上的位移。使用L1 Loss约束预测的位移图:
![[1] A Keypoint-based Global Association Network for Lane Detection_第3张图片](http://img.e-com-net.com/image/info8/497f8e0451db4c64ae126a2b99c65690.jpg)
3.1.2 车道线构建
![[1] A Keypoint-based Global Association Network for Lane Detection_第4张图片](http://img.e-com-net.com/image/info8/7a5770add6ca40f89c391bbecb803f8d.jpg)
车道线建构如上图所示。首先,如(a),对预测的关键点置信度图进行max pooling(1*3),在水平方向的局部区域选择置信度响应较大的点,作为关键点。然后把这些点组成有序序列:
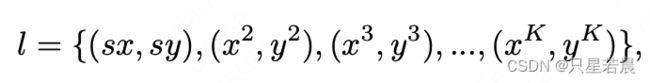
其中, ( s x , s y ) (sx, sy) (sx,sy)表示始点,其余点表示剩余的点。
为了获取每条车道线的始点,在位移图上选择值小于1的点作为始点,如(b)。局部区域内会存在多个候选始点,选择这些点的几何中心作为唯一的始点。始点即可初步表示每条车道线实例。
然后根据位移图计算每关键点对应的可能始点的位置(关键点本身的位置与位移之和,可以表示给该关键点预测的始点的位置,即 ( s x ′ , s y ′ ) (sx^{'},sy^{'}) (sx′,sy′)):

当每个关键点(非始点)预测的始点与直接预测(从位移图值小于1获得)的第i个始点的小于阈值 θ d i s \theta_{dis} θdis,如(c),则认为该关键点与该始点属于第i条车道线实例。然后把属于同一条实例的所有关键点按照顺序连接,生成最终的车道线。
3.2 车道级特征聚合
传统2D卷积不适用于车道线的线形结构。提出LFA模块来自适应聚合邻接点区域的信息,以增强每个关键点的特征表征。下图展示了LFA
![[1] A Keypoint-based Global Association Network for Lane Detection_第5张图片](http://img.e-com-net.com/image/info8/c6d7d39c004f4b1fa6f67165b71bde8a.jpg)
以某一关键点为例,模型首先用卷积层预测该点和它附近的同一条车道线上的 M M M个关键点的位移(位移是从该点的特征直接预测出来的):

p i p_i pi表示第 i i i个关键点的坐标, F ( p i ) F(p_i) F(pi)表示第i个关键点的特征, Δ P \Delta P ΔP表示预测的位移。然后,邻接点的特征整合后,使用可变形卷积来整合第 i i i个关键点的上下文:
![[1] A Keypoint-based Global Association Network for Lane Detection_第6张图片](http://img.e-com-net.com/image/info8/2481ac78b3114f5ba0ad6b90e01d8f55.jpg)
其中, p i p_i pi表示第 i i i个关键点的坐标, Δ p i m \Delta p_i^m Δpim表示第 i i i个关键点到第 m m m个邻接关键点的位移, ( p i + Δ p i m ) (p_i+\Delta p_i^m) (pi+Δpim)表示从第 i i i个关键点预测得到的第 m m m个邻接关键点的坐标。取该预测坐标局部区域的特征,然后乘以权重 w m w_m wm,得到第 i i i个关键点加权的上下文特征(根据前面预测的位移,找到邻接的 m m m个关键点的位置,提取每个位置的特征,然后加权相加,得到该点实际的上下文特征)。
为了增强LFA的性能,本文添加了辅助损失函数来监督 Δ P i \Delta P_i ΔPi。令第 i i i个关键点和所在线上的其他点的实际位移表示为 Δ G i = { Δ g i k ∣ k = 1 , . . . , K } \Delta G_i=\{\Delta g_i^k|k=1,...,K\} ΔGi={Δgik∣k=1,...,K}。 Δ g i k = g i k − p i \Delta g_i^k=g_i^k-p_i Δgik=gik−pi,即第 i i i个关键点与第第 k k k个关键点的位移。
为了计算损失值,需要给预测位移 Δ p i \Delta p_i Δpi(从当前关键点预测的与第 i i i个关键点之间的位移)与实际位移 Δ g i \Delta g_i Δgi(当前关键点与实际第 i i i个邻接关键点之间的位移)配对,采用匈牙利算法(Hungarian algorithm)进行配对,最小化损失值:
![[1] A Keypoint-based Global Association Network for Lane Detection_第7张图片](http://img.e-com-net.com/image/info8/5c7e413183d3483697a4949680c2d36c.jpg)
L m a t c h L_{match} Lmatch采用欧式距离计算。然后对配对后的位移采用SmoothL1 Loss监督:

其中, K K K表示每条车道线上采样关键点的数量, N N N表示车道线的数量, M M M为每个关键点的邻接关键点数量。
4. 实验
略
5.参考文献
[1] Wang J , Ma Y , Huang S , et al. A Keypoint-based Global Association Network for Lane Detection[J]. arXiv e-prints, 2022.
![[1] A Keypoint-based Global Association Network for Lane Detection_第8张图片](http://img.e-com-net.com/image/info8/d1575232739b4958b5a8230b839396fc.jpg)