机器学习的数学基础

前言

  数学是一切科学的基础， 可以说人类的每一次重大进步背后都是数学在后面强有力的支撑。 从第一次的工业革命到第三次的信息革命， 数学作为快速信息交换工具， 一直在促进我们生产力发展。 数学是一种工具学科， 是学习其他学科的基础。人工智能是建立在信息时代之上的新兴科技， 将成为新型产业带动时代的发展。要想了解并且深入学习人工智能方向的技术，必须了解一些基本的数学知识！

一、向量

1、标量

  标量（scalar），亦称“无向量”。有些物理量，只具有数值大小，而没有方向，部分有正负之分。物理学中，标量（或作纯量）指在坐标变换下保持不变的物理量。用通俗的说法，标量是只有大小，没有方向的量。

2、向量

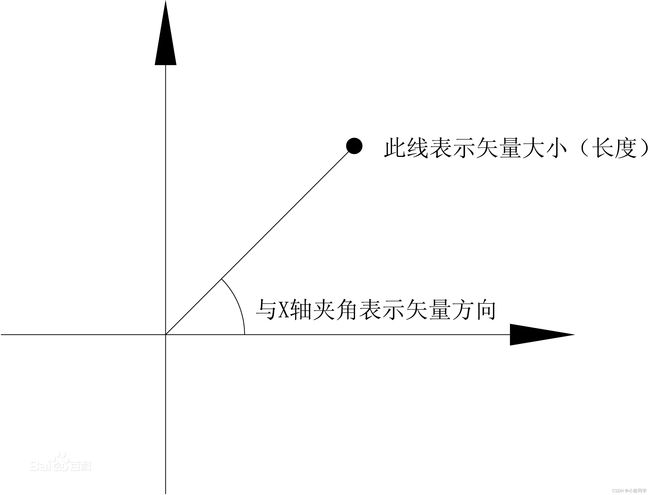
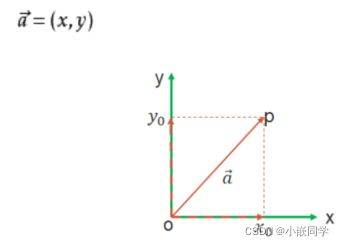
  在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量（物理学中称标量），数量（或标量）只有大小，没有方向。

二、线性变换

  线性映射（ linear mapping）是从一个向量空间V到另一个向量空间W的映射且保持加法运算和数量乘法运算，而线性变换（linear transformation）是线性空间V到其自身的线性映射。同时具有以下定义：线性空间V上的一个变换A称为线性变换，对于V中任意的元素α，β和数域P中任意k，都有

A(α+β)=A(α)+A(β)
A(kα)=kA(α)

性质
（1）设A是V的线性变换，则A(0)=0,A(-α)=-A(α)；
（2）线性变换保持线性组合与线性关系式不变；
（3）线性变换把线性相关的向量组变成线性相关的向量组。
注意：线性变换可能把线性无关的向量组变成线性相关的向量组。

判断一个变换是否是线性变换其实并不困难，只要判断这个变换是否满足加法不变性和数
乘不变性即可。

三、 矩阵

参考学习：http://t.zoukankan.com/icmzn-p-11176298.html

1、定义

  在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合 ，最早来自于方程组的系数及常数所构成的方阵。简单来说，矩阵就是充满数字的表格。

  由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

  这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。
  元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵

2、基本运算

(1)矩阵加减法

  两个矩阵相加或相减，需要满足两个矩阵的列数和行数一致。

  加法交换律： A + B = B + A

(2)矩阵乘法
  两个矩阵A和B相乘，需要满足A的列数等于B的行数

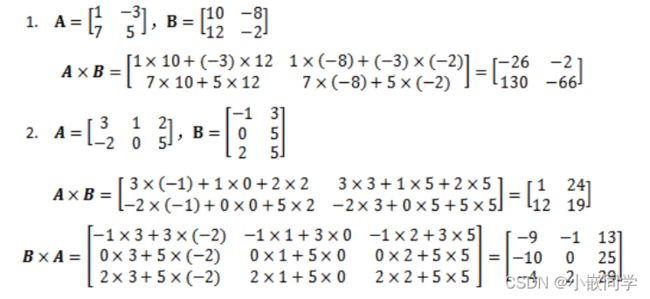
(3)数乘


矩阵的加减法和矩阵的数乘合称矩阵的线性运算

(4)转置
  把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵AT，这一过程称为矩阵的转置.

3、单位矩阵

  单位矩阵是一个n×n矩阵，从左到右的对角线上的元素是1，其余元素都为0。下面是三个单位矩阵：

  如果A是n×n矩阵， I是单位矩阵，则AI= A, IA = A，单位矩阵在矩阵乘法中的作用相当于数字1。

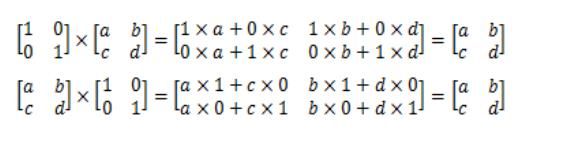
4、逆矩阵

  矩阵A的逆矩阵记作A-1， A A-1=A-1A= I， I是单位矩阵。

  单位矩阵的逆矩阵是它本身。

5、奇异矩阵

  当一个矩阵没有逆矩阵的时候，称该矩阵为奇异矩阵。当且仅当一个矩阵的行列式为零时，该矩阵是奇异矩阵。

当ad-bc=0时， |A|没有定义， A-1不存在， A是奇异矩阵。

6、对称矩阵

  如果一个矩阵转置后等于原矩阵，那么这个矩阵称为对称矩阵。
一个矩阵转置和这个矩阵的乘积就是一个对称矩阵。

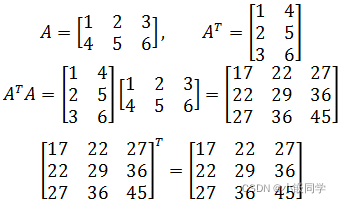
7、欧式变换

欧氏变换由两部分组成：
• 旋转
• 平移

8、齐次坐标

  简而言之，齐次坐标就是用N+1维来代表N维坐标。我们可以在一个2D坐标末尾加上一个额外的变量w来形成2D齐次坐标。因此，一个点(X,Y)在齐次坐标里面变成了（x,y,w），并且有：
X = x/w
Y = y/w

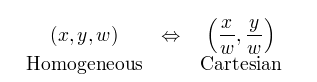
例如：
（1，2）的齐次坐标可以表示为（1，2，1）。如果点（1，2）移动到无限远处，在笛卡尔坐标下它变为(∞,∞)，然后它的齐次坐标表示为（1，2，0），因为(1/0, 2/0) = (∞,∞)，我们可以不用”∞"来表示一个无穷远处的点了

四、导数&偏导数

1、导数、偏导数

导数（微分）： 是代表函数（曲线）的斜率，是描述函数（曲线）变化快慢的量，同时曲线的极大值点也可以使用导数来判断，即极大值点的导数为0，此时斜率为零。
偏导数： 是指在多元函数的情况下，对其每个变量进行求导，求导时，把其他变量看做常量进行处理，物理意义就是查看这一个变量在其他情况不变的情况下对函数的影响程度。

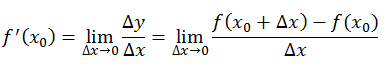
2、梯度

梯度: 梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）

  简而言之，对多元函数的各个自变量求偏导数，并把求得的这些偏导数写成向量形式，就是梯度

梯度下降法：是一种寻找函数极小值的方法。

  该方法最普通的做法是：在已知参数当前值的情况下，按当前点对应的梯度向量的反方向(正方向是求最大值的)，并按事先给定好的步长大小，对参数进行调整。

  按如上方法对参数做出多次调整之后，函数就会逼近一个极小值。

梯度下降法存在的问题：
  1.参数调整缓慢
  2.收敛于局部最小值

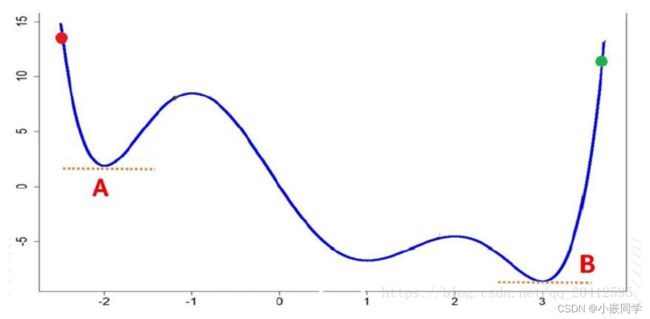
  A为局部最小值，而B为全局最小值，若步长设置不恰当，则容易认为A是最小值，出现局部收敛

五、概率学基础

  Machine Learning与Traditional statistical analyses的一些区别，主要在关注主体和验证性作区分。前者不关心模型的复杂度有多么的高，仅仅要求模型有良好的泛化性以及准确性。而后者在模型本身有一定的要求——不可过于复杂。

1、事件与关系运算

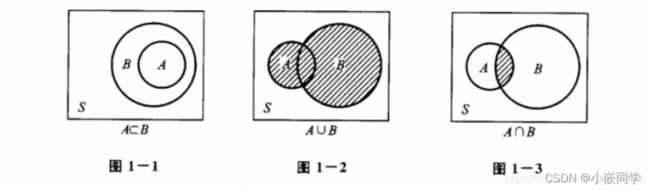
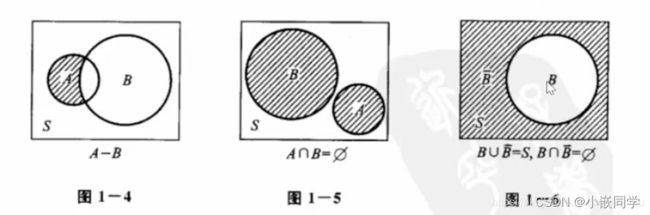
A-B=A -（A交B），意思是在A中把A与B公有的元素去掉

2、事件运算定律

3、概率的基本概念

(1) 概率：事件发生的可能性大小的度量，其严格定义如下：

  概率P(g)为定义在事件集合上的满足下面2个条件的函数：
  • 1)对任何事件A， P(A) >= 0
  • 2)对必然事件B， P(B) = 1

(2) 概率的基本性质:

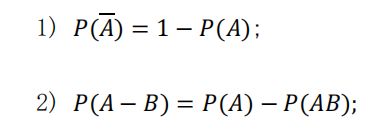
(3) 古典型概率: 实验的所有结果只有有限个，且每个结果发生的可能性相同，其概率计算公式：

(4)独立性
  事件独立性（independence of event），事件A的发生与事件B发生的概率无关的状态。

  事件A与B独立的条件， AB同时发生的概率和A单独发生以及B单独发生的概率是一样的

(5)离散：离散就是不连续

4、数学期望、方差、标准差

(1)数学期望（均值）：表示一件事平均发生的概率，记为E(x), E(x) = x1p1+x2p2+…+ xnpn。或者：

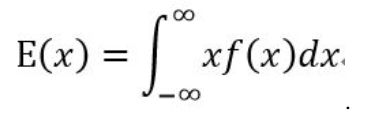
(2) 方差：用来刻画随机变量x和数学期望E(x)之间的偏离程度，记做D(x)。

方差计算公式（非概率问题时常用的一个，小学、初高中数学统计知识中常用）：


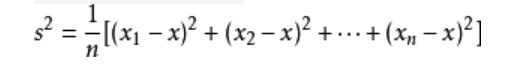
(3)标准差（均方差）：标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。

5、正态分布（高斯分布）

  正态分布：若随机变量X服从一个数学期望为μ、方差为σ^2 (这个2表示平方)
的正态分布，记为N(μ， σ^2)。

  μ决定了其位置（中心线），其标准差σ决定了分布的幅度（胖瘦）。

  标准正态分布：当μ = 0， σ = 1时的正态分布是标准正态分布

六、熵 entropy

(1)信息量：信息量是指信息多少的度量。

  1928年，R．V．L．哈特莱提出了信息定量化的初步设想，他将符号取值数m的对数定义为信息量，即I=log2m(以2为底取对数)。对信息量作深入、系统研究的是信息论创始人C．E．香农。1948年，香农指出信源给出的符号是随机的，信源的信息量应是概率的函数，以信源的信息熵表示，即，其中Pi表示信源不同种类符号的概率，i= 1，2，…，n。

  例如，若一个连续信源被等概率量化为4层，即4 种符号。这个信源每个符号所给出的信息量应为，与哈特莱公式I=log2m=log24=2bit一致。实质上哈特莱公式是等概率时香农公式的特例。

(2)物理学上，是“混乱” 程度的量度。
  系统越有序，熵值越低；系统越混乱或者分散，熵值越高。

(3)信息理论：
  1、当系统的有序状态一致时，数据越集中的地方熵值越小，数据越分散的地方熵值越大。这是从信息的完整性上进行的描述。

  2、当数据量一致时，系统越有序，熵值越低；系统越混乱或者分散，熵值越高。这是从信息的有序性上进行的描述。

  若不确定性越大，则信息量越大，熵越大
  若不确定性越小，则信息量越小，熵越小

（3）假如事件A的分类划分是（A1,A2,…,An），每部分发生的概率是(p1,p2,…,pn)，那信息熵定义为公式如下：

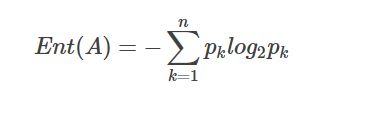
七、kl散度（相对熵）

KL 散度是一种衡量两个概率分布的匹配程度的指标，两个分布差异越大， KL散度越大。

KL散度的用途：比较两个概率分布的接近程度。

定义如下：

本文章参考了百度百科、他人技术博客、八斗学院免费教程资料等综合整理而来，如有侵权，联系删除！水平有限，欢迎各位指导交流！