《剑指offer》题解——week3（持续更新）

❤ 作者主页：Java技术一点通的博客
❀ 个人介绍：大家好，我是Java技术一点通！(￣▽￣)~*
❀ 微信公众号：Java技术一点通
记得点赞、收藏、评论⭐️⭐️⭐️
认真学习!!!

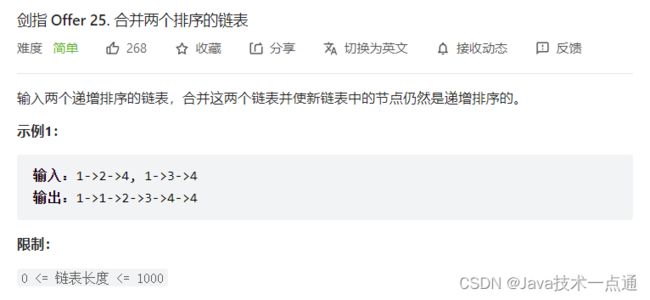
一、剑指 Offer 25. 合并两个排序的链表

1. 题目描述

2. 思路分析

(线性合并) O(n)
1. 新建头部的保护结点dummy，设置cur 指针指向dummy。
2. 若当前$l_1$指针指向的结点的值val比$l_2$指针指向的结点的值val小 ，则令cur的next指针指向$l_1$，且$l_1$后移；否则指向$l_2$，且 $l_2$后移。
3. 然后cur指针按照上一部设置好的位置后移。
4. 循环以上步骤直到$l_1$或$l_2$为空。
5. 将剩余的$l_1$或$l_2$接到cur指针后边。

3. 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        auto dummy = new ListNode(-1), cur = dummy;
        while (l1 && l2) {
            if (l1->val < l2->val) {
                cur = cur->next = l1;
                l1 = l1->next;
            } else {
                cur = cur->next = l2;
                l2 = l2->next;
            }
        }
        if (l1) cur->next = l1;
        if (l2) cur->next = l2;
        return dummy->next;
    }
};

 
 

二、剑指 Offer 26. 树的子结构

1. 题目描述

2. 思路分析

1. 首先判断两个二叉树为空的情况，如果为空，直接return false;
2. 如果不为空，就可以调用isSame(A, B)函数来判断B是否为A的子树。如果不是，则递归，判断B是否是A的左子树的子树，或者，B是否是A的右子树的子树。注意是||
3. 对于函数isSame(A, B)的细节。首先判断B子树的节点是否为空，如果为空，说明前面的都匹配，直接return true;
4. 接下来，如果B树的节点不为空，但是A树的节点为空，那么一定不匹配，直接return false;
5. 如果A和B树的节点都不为空，但是值不一样，那也是不匹配，直接return false;
6. 最后如果 B树的节点不为空， A树的节点也不为空， A树和B树的当前节点是匹配的。那么我们就递归到A和B的左子树，同时，A和B的右子树，看看是否匹配，注意这里是&&。

注意：isSame()中的顺序不能改：

1. 先判断B的节点是否为空，是的话说明该节点的父节点已经匹配，return true；
2. 这时，再判断A的节点是否为空，走到这句说明B的节点不为空，如果A空B不空，一定不匹配，return false;
3. 第3句，说明A和B都不为空，就看对应的val是否相等，不等就return false；相等的话就向下递归，看这个节点在2棵树中对应的左右子树是否匹配。

3. 代码实现

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
   bool isSubStructure(TreeNode* A, TreeNode* B) {
       if (!A || !B) return false;
       if (isSame(A, B)) return true;
       return isSubStructure(A->left, B) || isSubStructure(A->right,B);
   }
    bool isSame(TreeNode* p1, TreeNode* p2) {
       if (!p2) return true;
       if (!p1 || p1->val != p2->val) return false;
       return isSame(p1->left, p2->left) && isSame(p1->right, p2->right);
   }
};

 
 

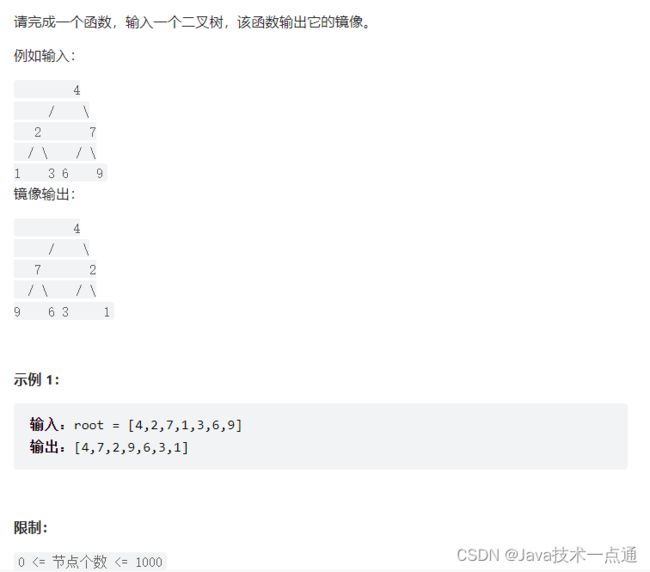
三、剑指 Offer 27. 二叉树的镜像

1. 题目描述

2. 思路分析

这是一道很经典的二叉树问题。显然，我们从根节点开始，递归地对树进行遍历，并从叶子节点先开始翻转得到镜像。如果当前遍历到的节点 root 的左右两棵子树都已经翻转得到镜像，那么我们只需要交换两棵子树的位置，即可得到以 root 为根节点的整棵子树的镜像。

3. 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if (root == NULL) return NULL;
        TreeNode *left = mirrorTree(root->left);
        TreeNode *right = mirrorTree(root->right);
        root->left = right;
        root->right = left;
        return root;
    }
};

四、剑指 Offer 28. 对称的二叉树

1. 题目描述

2. 思路分析

如果一个树的左子树与右子树镜像对称，那么这个树是对称的。
因此，该问题可以转化为：两个树在什么情况下互为镜像？
如果同时满足下面的条件，两个树互为镜像：

1. 它们的两个根结点具有相同的值；
2. 每个树的右子树都与另一个树的左子树镜像对称。

我们可以实现这样一个递归函数，通过同步移动两个指针的方法来遍历这棵树，p 指针和 q 指针一开始都指向这棵树的根，随后 p 右移时，q 左移，p 左移时，q 右移。每次检查当前 p 和 q 节点的值是否相等，如果相等再判断左右子树是否对称。

3. 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }

    bool check(TreeNode *p, TreeNode *q) {
        if (!p && !q) return true;
        if (!p || !q) return false;
        return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
    }
};

 
 

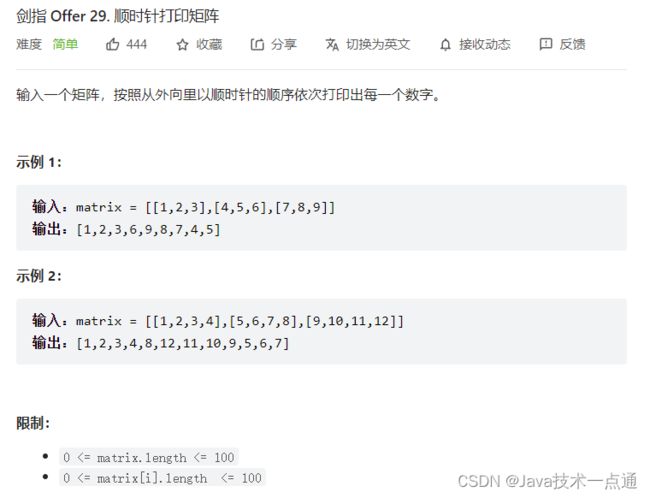
五、剑指 Offer 29. 顺时针打印矩阵

1. 题目描述

2. 思路分析

我们顺时针定义四个方向：上右下左。
从左上角开始遍历，先往右走，走到不能走为止，然后更改到下个方向，再走到不能走为止，依次类推，遍历 $n^2$个格子后停止。

3.代码实现

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        vector res;
        int n = matrix.size();
        if (!n) return res;
        int m = matrix[0].size();

        int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};
        vector> st(n, vector(m));

        for (int i = 0, x = 0, y = 0, d = 0; i < n * m; i ++ ) {
            res.push_back(matrix[x][y]);
            st[x][y] = true;

            int a = x + dx[d], b = y + dy[d];
            if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) {
                d = (d + 1) % 4;
                a = x + dx[d], b = y + dy[d];
            }
            x = a, y = b;
        }
        return res;
    }
};

 
 

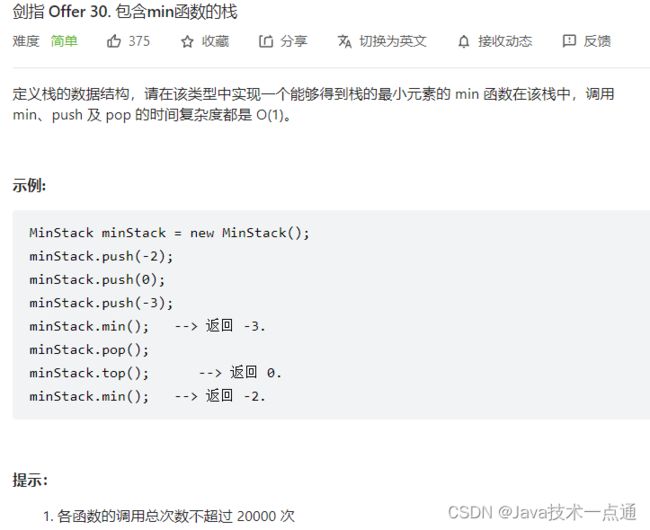
六、剑指 Offer 30. 包含min函数的栈

1. 题目描述

2. 思路分析

我们除了维护基本的栈结构之外，还需要维护一个单调栈，来实现返回最小值的操作。
下面介绍如何维护单调栈：

1. 当我们向栈中压入一个数时，如果该数 ≤ 单调栈的栈顶元素，则将该数同时压入单调栈中；否则，不压入，这是由于栈具有先进后出性质，所以在该数被弹出之前，栈中一直存在一个数比该数小，所以该数一定不会被当做最小数输出。
2. 当我们从栈中弹出一个数时，如果该数等于单调栈的栈顶元素，则同时将单调栈的栈顶元素弹出。
3. 单调栈由于其具有单调性，所以它的栈顶元素，就是当前栈中的最小数。

3. 代码实现

class MinStack {
public:
    /** initialize your data structure here. */
    stack stackValue;
    stack stackMin;
    MinStack() {

    }
    
    void push(int x) {
        stackValue.push(x);
        if (stackMin.empty() || stackMin.top() >= x) 
            stackMin.push(x);
    }
    
    void pop() {
        if (stackMin.top() == stackValue.top()) stackMin.pop();
        stackValue.pop();
    }
    
    int top() {
        return stackValue.top();
    }
    
    int min() {
        return stackMin.top();
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(x);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->min();
 */

 
 

七、剑指 Offer 31. 栈的压入、弹出序列

1. 题目描述

2. 思路分析

借用一个辅助栈stack ，模拟 压入 / 弹出操作的排列。根据是否模拟成功，即可得到结果。

• 入栈操作： 按照压栈序列的顺序执行。
• 出栈操作： 每次入栈后，循环判断 “栈顶元素 == 弹出序列的当前元素” 是否成立，将符合弹出序列顺序的栈顶元素全部弹出。

算法流程：

1. 初始化： 辅助栈 stack ，弹出序列的索引 index ；
2. 遍历压栈序列： 各元素记为 num` ；
   1. 元素 num 入栈；
   2. 循环出栈：若 stack 的栈顶元素 == 弹出序列元素 popped[index] ，则执行出栈与 index ++ ；
3. 返回值： 若 stack 为空，则此弹出序列合法。

3. 代码实现

class Solution {
public:
    bool validateStackSequences(vector& pushed, vector& popped) {
        if (pushed.size() != popped.size()) return false;
        stack stack;
        int index = 0;
        for (int num : pushed) {
            stack.push(num);
            while (!stack.empty() && stack.top() == popped[index]) {
                stack.pop();
                index ++;
            }
        }
        return stack.empty();
    }
};

 
 

八、剑指 Offer 32 - I. 从上到下打印二叉树

1. 题目描述

2. 思路分析

题目要求的二叉树的 从上至下 打印（即按层打印），又称为二叉树的 广度优先搜索（BFS）。
BFS 通常借助 队列 的先入先出特性来实现。
算法流程：

1. 特例处理： 当树的根节点为空，则直接返回空列表 [] ；
2. 初始化： 打印结果列表 res ，包含根节点的队列 queue[root]；
3. BFS 循环： 当队列 queue 为空时跳出；
   1. 出队： 队首元素出队，记为 t；
   2. 打印： 将 t.val 添加至列表 res尾部；
   3. 添加子节点： 若 t 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
4. 返回值： 返回打印结果列表 res 即可。

3. 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector levelOrder(TreeNode* root) {
        vector res;
        if (!root) return res;
        queue q;
        q.push(root);

        while (q.size()) {
            auto t = q.front();
            q.pop();
            res.push_back(t->val);
            if (t->left) q.push(t->left);
            if (t->right) q.push(t->right);
        }
        return res;
    }
};

 
 

九、剑指 Offer 32 - II. 从上到下打印二叉树 II

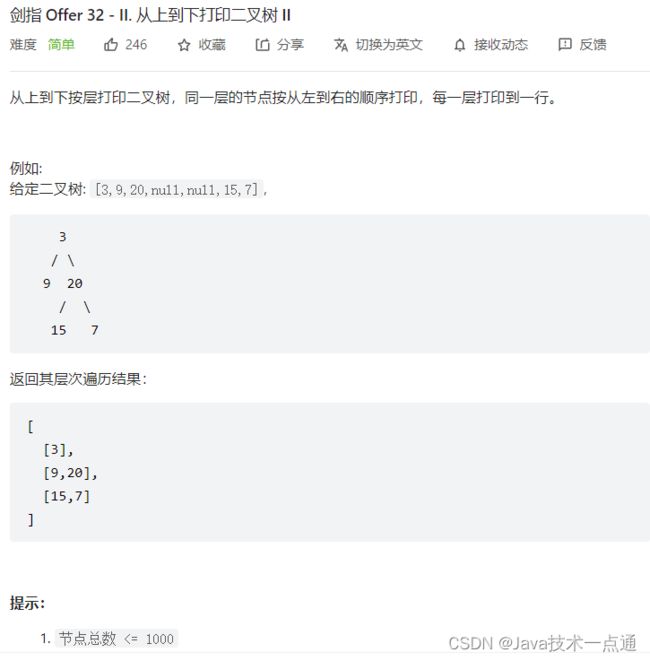
1. 题目描述

2. 思路分析

本题是要求将本层全部节点打印到一行，并将下一层全部节点加入队列，以此类推，即可分为多行打印。
算法流程：

1. 特例处理： 当树的根节点为空，则直接返回空列表 [] ；
2. 初始化： 打印结果列表 res ，包含根节点的队列 queue[root]；
3. BFS 循环： 当队列 queue 为空时跳出；
   1. 新建一个临时列表 tmp ，用于存储当前层打印结果；
   2. 当前层打印循环： 循环次数为当前层节点数（即队列 queue 长度）；
      1. 出队： 队首元素出队，记为 t；
      2. 打印： 将 t.val 添加至列表 res尾部；
      3. 添加子节点： 若 t 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
   3. 将当前层结果 tmp 添加入 res 。
4. 返回值： 返回打印结果列表 res 即可。

3. 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> res;
        if (!root) return res;
        queue q;
        q.push(root);
        while (q.size()) {
            vector tmp;
            int n = q.size();
            for (int i = 0; i < n; i ++ ) {
                auto p = q.front();
                q.pop();
                tmp.push_back(p->val);
                if (p->left) q.push(p->left);
                if (p->right) q.push(p->right);
            }
            res.push_back(tmp);
        }
        return res;
    }
};

 
 

十、剑指 Offer 32 - III. 从上到下打印二叉树 III

1. 题目描述

2. 思路分析

层序遍历 + 倒序
此方法的优点是只用列表即可，无需其他数据结构。
偶数层倒序： 若 res 的长度为 奇数 ，说明当前是偶数层，则对 tmp 执行 倒序 操作。

3. 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> res;
        if (!root) return res;
        queue q;
        q.push(root);
        while (q.size()) {
            int n = q.size();
            vector tmp;
            for (int i = 0; i < n; i ++ ) {
                auto t = q.front();
                q.pop();
                tmp.push_back(t->val);
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
            if (res.size() % 2 == 1) reverse(tmp.begin(), tmp.end());
            res.push_back(tmp);
        }
        return res;
    }
};

 
 

创作不易，如果有帮助到你，请给文章点个赞和收藏，让更多的人看到！！！
关注博主不迷路，内容持续更新中。