《剑指offer》题解——week6（持续更新）

❤ 作者主页：Java技术一点通的博客
❀ 个人介绍：大家好，我是Java技术一点通！(￣▽￣)~*
❀ 微信公众号：Java技术一点通
记得点赞、收藏、评论⭐️⭐️⭐️
认真学习!!!

一、剑指 Offer 53 - II. 0～n-1中缺失的数字

1. 题目描述

2. 思路分析

排序数组中的搜索问题，首先想到 二分法 解决。
假设我们缺失的元素数值为 $x$，那么对于 $x$ 左边的元素（若有）必然是完整且连续的，也就是其必然满足 $nums[i]=i$，而其右边的元素（若有）必然由于 x 的缺失，导致必然不满足 $nums[i]=i$，因此在以缺失元素为分割点的数轴上，具有二段性，我们可以使用 「二分」 来找该分割点。
同时由于缺失元素可能是 $[0,n-1]$ 范围内的最大值，因此我们需要 二分结束后 再 $check$ 一次，若不满足，说明缺失的元素值为 $n-1$。

3. 代码实现

class Solution {
public:
    int missingNumber(vector& nums) {
        int l = 0, r = nums.size() - 1;
        while (l < r) {
            int mid = (l + r + 1) / 2;
            if (nums[mid] == mid) l = mid;
            else r = mid - 1;
        }
        if (nums[r] == r) r ++;
        return r;
    }
};

 
 

二、剑指 Offer 54. 二叉搜索树的第k大节点

1. 题目描述

2. 思路分析

基于此性质： 二叉搜索树的中序遍历为 递增序列 。

• 根据以上性质，易得二叉搜索树 中序遍历倒序 为 递减序列。
• 因此，求 “二叉搜索树第 $k$ 大的节点” 可转化为求 “此树的中序遍历倒序的第 $k$ 个节点”。

算法流程：

1. 终止条件： 当节点 $root$ 为空（越过叶节点），则直接返回；
2. 递归右子树： 即 dfs(root->right);
3. 为求第 $k$ 个节点，需要实现以下 三个步骤 ：
   1. 提前返回： 若 $k=0$ ，代表已找到目标节点，无需继续遍历，因此直接返回；
   2. 统计序号： 执行 $k=k-1$ （即从 $k$ 减至 0 ）；
   3. 记录结果： 若 $k=0$ ，代表当前节点为第 $k$ 大的节点，因此记录 $res=root.value$ ；
4. 递归左子树： 即 dfs(root->left)。

3. 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int res;
    int kthLargest(TreeNode* root, int k) {
        dfs(root, k);
        return res;
    }

    void dfs(TreeNode* root, int &k) {
        if (root == NULL) return;
        dfs(root->right, k);
        if (--k == 0) {
            res = root->val;
            return;
        }
        dfs(root->left, k);
    }
};

 
 

三、剑指 Offer 55 - I. 二叉树的深度

1. 题目描述

2. 思路分析

关键点： 此树的深度和其左（右）子树的深度之间的关系。显然，此树的深度 等于 左子树的深度 与 右子树的深度 中的 最大值 +1 。

算法流程：

1. 终止条件： 当 $root$​ 为空，说明已越过叶节点，因此返回 深度 0 。
2. 递推工作： 本质上是对树做后序遍历。
   1. 计算节点 $root$​ 的 左子树的深度 ，即调用 maxDepth(root->left)；
   2. 计算节点 $root$​ 的 右子树的深度 ，即调用 maxDepth(root->right)；
3. 返回值： 返回 此树的深度 ，即 max(maxDepth(root->left), maxDepth(root->right)) + 1。

3. 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (!root) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

 
 

四、剑指 Offer 55 - II. 平衡二叉树

1. 题目描述

2. 思路分析

平衡二叉树的定义是：二叉树的每个节点的左右子树的高度差的绝对值不超过 1，则二叉树是平衡二叉树。
根据定义，一棵二叉树是平衡二叉树，当且仅当其所有子树也都是平衡二叉树，因此可以使用递归的方式判断二叉树是不是平衡二叉树。

定义函数 $height$， 用于计算二叉树中的任意一个节点 $p$ 的高度：
$$height(p)=\{\begin{array}{l}0,p是空节点\\ max(height(p->left),height(p->right))+1,p是非空节点\end{array}$$

有了计算节点高度的函数，即可判断二叉树是否平衡。具体做法类似于二叉树的前序遍历，即对于当前遍历到的节点，首先计算左右子树的高度，如果左右子树的高度差是否不超过 1，再分别递归地遍历左右子节点，并判断左子树和右子树是否平衡。

3. 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if (!root) return true;
        else return abs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }

    int height(TreeNode* root) {
        if (!root) return 0;
        else return max(height(root->left), height(root->right)) + 1;
    }

};

 
 

五、剑指 Offer 56 - I. 数组中数字出现的次数

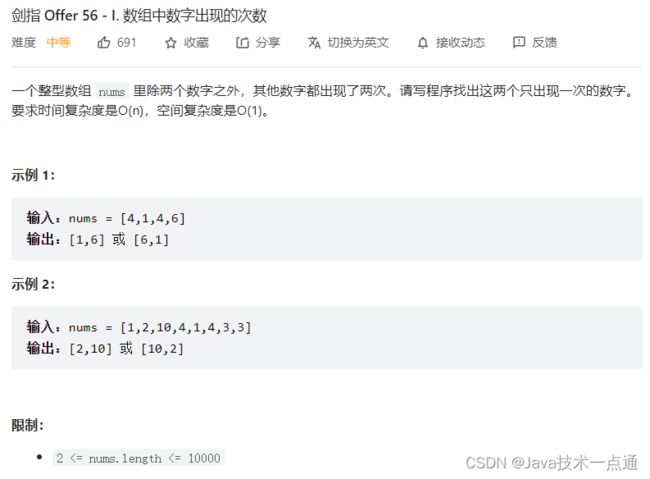
1. 题目描述

2. 思路分析

设整型数组 $nums$ 中出现一次的数字为 $x$ ，出现两次的数字为 $a,a,b,b,...$ ，即：$nums=[a,a,b,b,...,x]$
异或运算有个重要的性质，两个相同数字异或为 0 ，即对于任意整数 $a$ 有 $a\oplus a=0$ 。因此，若将 $nums$ 中所有数字执行异或运算，留下的结果则为 出现一次的数字 $x$ ，即：
$a\oplus a\oplus b\oplus b...\oplus x$
=$0\oplus 0\oplus ...\oplus x$
=$x$

本题难点：数组 $nums$ 有 两个 只出现一次的数字，因此无法通过异或直接得到这两个数字。

设两个只出现一次的数字为 $x,y$ ，由于 $x\ne y$ ，则 $x$ 和 $y$ 二进制至少有一位不同（即分别为 0 和 1 ），根据此位可以将 $nums$ 拆分为分别包含 $x$ 和 $y$ 的两个子数组。
易知两子数组都满足 「除一个数字之外，其他数字都出现了两次」。因此，仿照以上简化问题的思路，分别对两子数组遍历执行异或操作，即可得到两个只出现一次的数字 $x$, $y$ 。

算法流程：

1. 遍历 $nums$ 执行异或：

   • 设整型数组 $nums=[a,a,b,b,...,x,y]$ ，对 $nums$ 中所有数字执行异或，得到的结果为 $x\oplus y$ ，即：
     $a\oplus a\oplus b\oplus b...\oplus x\oplus y$
     =$0\oplus 0\oplus ...\oplus x\oplus y$
     =$x\oplus y$

2. 循环左移计算 $m$ ：

   • 根据异或运算定义，若整数 $x\oplus y$ 某二进制位为 1 ，则 $x$ 和 $y$ 的此二进制位一定不同。换言之，找到 $x\oplus y$ 某为 1 的二进制位，即可将数组 $nums$ 拆分为上述的两个子数组。根据与运算特点，可知对于任意整数 $a$ 有：

     • 若 $a\&0001=1$ ，则 $a$ 的第一位为1 ；
     • 若 $a\&0010=1$ ，则 $a$ 的第二位为1 ；
     • 依次类推…

   • 因此，初始化一个辅助变量 $m=1$ ，通过与运算从右向左循环判断，可 获取整数 $x\oplus y$ 首位 1 ，记录于 $m$ 中;

3. 拆分 $nums$ 为两个子数组：

4. 分别遍历两个子数组执行异或：

   • 通过遍历判断 $nums$ 中各数字和 $m$ 做与运算的结果，可将数组拆分为两个子数组，并分别对两个子数组遍历求异或，则可得到两个只出现一次的数字。

5. 返回值： 返回只出现一次的数字 $x,y$ 即可。

3. 代码实现

class Solution {
public:
    vector singleNumbers(vector& nums) {
        int x = 0, y = 0, n = 0, m = 1;
        for (int num : nums) n ^= num;
        while ((n & m) == 0) m <<= 1;
        for (int num : nums) {
            if (num & m) x ^= num;
            else y ^= num;
        }
        return vector {x, y};
    }
};

 
 

六、剑指 Offer 56 - II. 数组中数字出现的次数 II

1. 题目描述

2. 思路分析

状态转移：
本题与前一题思路类似，前一题中，其他数都出现了两次，因此需要的状态转移方式是，如果出现两个 1 就抵消为 0 ，用一个变量和异或运算即可实现，而本题是需要 1 出现三次时才会抵消，因此有三种状态，即 1 出现的次数为 $3k,3k+1,3k+2$ 次。
逐个位来看，要设计一个两位的状态转移，出现三个 1 时，循环抵消，出现 0 时不变，一个变量只能记录两种状态，因此要用两个变量来记录状态，用 $one$ 和 $two$ 两个变量来记录1出现次数。
00 表示 1 出现 $3k$ 次，01表示 1 出现 $3k+1$ 次，10 表示 1 出现 $3k+2$ 次。

真值表
two   one   x   two    one
0      0    1    0     1
0      1    1    1     0
1      0    1    0     0
0      0    0    0     0
0      1    0    0     1
1      0    0    1     0

先看 $one$ 的状态转移方程:

one = (~one & ~two & x) | (one & ~two & ~x)
= ~two & ((~one & x) | (one & ~x))
= ~two & (one ^ x)

同理，再用转移后的 $one$ 来求 $two$ 的状态转移方程。
这里，$one$ 为当且仅当 1 出现次数为 $3k+1$, $tow$ 为当且仅当 1 出现次数为 $3k+2$。
因此如果题目改为，有一个数出现了两次，则返回 $two$即可。

3. 代码实现

class Solution {
public:
    int findNumberAppearingOnce(vector& nums) {
        int one=0,two=0;
        for(auto x:nums)
        {
            one=(one^x)&~two;
            two=(two^x)&~one;
        }
        return one;
    }
};

 
 

七、剑指 Offer 57. 和为s的两个数字

1. 题目描述

2. 思路分析

创建一个哈希表，对于每一个 $x$，我们首先查询哈希表中是否存在 $target-x$，如果有返回$[x,target-x]$。如果没有，将 $x$ 插入到哈希表中。

3. 代码实现

class Solution {
public:
    vector twoSum(vector& nums, int target) {
         unordered_set hash;
        for (auto x : nums)
        {
            if (hash.count(target - x)) return {target - x, x};
            hash.insert(x);
        }
        return {};
    }
};

 
 

八、剑指 Offer 57 - II. 和为s的连续正数序列

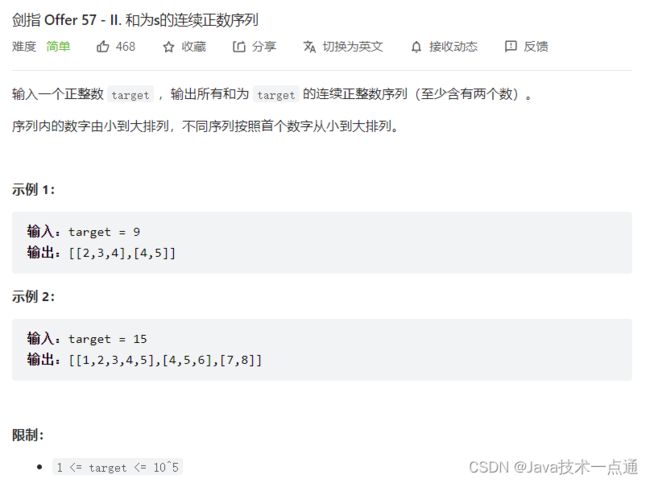
1. 题目描述

2. 思路分析

滑动窗口（双指针）:
设连续正整数序列的左边界 $i$ 和右边界 $j$ ，则可构建滑动窗口从左向右滑动。循环中，每轮判断滑动窗口内元素和与目标值 $target$ 的大小关系，若相等则记录结果，若大于 $target$ 则移动左边界 $i$ （以减小窗口内的元素和），若小于 $target$ 则移动右边界 $j$ （以增大窗口内的元素和）。

算法流程：

1. 初始化： 左边界 $i=1$，有边界 $j=2$，元素和 $s=3$，结果列表 $res$；

2. 循环：当 $i\ge j$时跳出；

   • 当 $s>target$ 时：向右移动左边界 $i=i+1$，并更新元素和 $s$；
   • 当 $s<target$ 时：向右移动右边界 $j=j+1$，并更新元素和 $s$；
   • 当 $s=target$ 时：记录连续整数序列，并向右移动左边界 $i=i+1$；

3. 返回值： 返回结果列表 $res$。

3. 代码实现

class Solution {
public:
    vector> findContinuousSequence(int target) {
        int i = 1, j = 2, s = 3;
        vector> res;
        while (i < j) {
            if (s == target) {
                vector ans;
                for (int k = i; k <= j; k ++ ) 
                    ans.push_back(k);
                res.push_back(ans);
            }
            if (s >= target) {
                s -= i;
                i ++;
            } else {
                j ++;
                s += j;
            }
        }
        return res;
    }
};

 
 

九、剑指 Offer 58 - I. 翻转单词顺序

1. 题目描述

2. 思路分析

解题方法：双指针
算法流程：

1. 倒序遍历字符串 $s$，记录单词左右索引边界 $left,right$；
2. 每确定一个单词的边界，则将其添加至单词列表 $res$；
3. 最后，将单词列表返回即可。

3. 代码实现

class Solution {
public:
    string reverseWords(string s) {
        string res;
        int n = s.size();
        if (!n) return res;
        int right = n - 1;
        while (right >= 0) {
            //从后往前寻找第一个字符
            while (right >= 0 && s[right] == ' ') right --;
            if (right < 0) break;

            // 从后往前寻找第一个空格
            int left = right;
            while (left >= 0 && s[left] != ' ') left --;

            // 添加单词到结果集
            res += s.substr(left + 1, right - left);
            res += ' ';

            right = left;
        }

        // 去除最后一个字符空格
        if (!res.empty()) res.pop_back();
        return res;
    }
};

 
 

十、剑指 Offer 58 - II. 左旋转字符串

1. 题目描述

2. 思路分析

算法流程：

1. 定义一个字符串结果集 $res$；
2. 先向 $res$ 中添加“第 $n+1$ 位至末位的字符”；
3. 再向 $res$ 中添加“首位至第 $n$ 位的字符”；
4. 直接将 $res$ 返回即可。

3. 代码实现

class Solution {
public:
    string reverseLeftWords(string s, int n) {
        string res;
        for (int i = n; i < s.size(); i ++ ) {
            res += s[i];
        }
        for (int i = 0; i < n; i ++ ) {
            res += s[i];
        }
        return res;
    }
};

 
 

创作不易，如果有帮助到你，请给文章点个赞和收藏，让更多的人看到！！！
关注博主不迷路，内容持续更新中。