pytorch学习记录

0.引言

一步一步积累吧。

• 一篇不错的博客

1.numpy 简单入门

1.1.常用基础

• numpy中文手册

• numpy官方简要入门

（1）数组基础

• 创建一个数组

# 1D Array
a = np.array([0, 1, 2, 3, 4])
b = np.array((0, 1, 2, 3, 4))
c = np.arange(5)
# linspace 函数创建一个指定范围内的等差数列。在这个例子中，范围是从0到 2*np.pi，数列的元素个数为5。
d = np.linspace(0, 2*np.pi, 5)

print(a) # >>>[0 1 2 3 4]
print(b) # >>>[0 1 2 3 4]
print(c) # >>>[0 1 2 3 4]
print(d) # >>>[ 0.          1.57079633  3.14159265  4.71238898  6.28318531]
print(a[3]) # >>>3

• 多维数组切片

# MD slicing
print(a[0, 1:4]) # >>>[12 13 14]
print(a[1:4, 0]) # >>>[16 21 26]
print(a[::2,::2]) # >>>[[11 13 15]
                  #     [21 23 25]
                  #     [31 33 35]]
print(a[:, 1]) # >>>[12 17 22 27 32]

• 数组属性

# Array properties
a = np.array([[11, 12, 13, 14, 15],
              [16, 17, 18, 19, 20],
              [21, 22, 23, 24, 25],
              [26, 27, 28 ,29, 30],
              [31, 32, 33, 34, 35]])

print(type(a)) # >>>
print(a.dtype) # >>>int64  返回数组元素的类型
print(a.size) # >>>25
print(a.shape) # >>>(5, 5) 数组的形状是它有多少行和列，上面的数组形状是(5，5)
print(a.itemsize) # >>>8  返回数组中每个元素的字节数
print(a.ndim) # >>>2 属性是数组的维数
print(a.nbytes) # >>>200 返回数组中所有元素所占用的字节数总和。

（2）使用数组

• 基本操作符

# Basic Operators
a = np.arange(25)  # 从0开始，步长为1，计数25个
a = a.reshape((5, 5))

b = np.array([10, 62, 1, 14, 2, 56, 79, 2, 1, 45,
              4, 92, 5, 55, 63, 43, 35, 6, 53, 24,
              56, 3, 56, 44, 78])
b = b.reshape((5,5))
#除了 dot() 之外，这些操作符都是对数组进行逐元素运算。比如 (a, b, c) + (d, e, f) 的结果就是 (a+d, b+e, c+f)
print(a + b)
print(a - b)
print(a * b)
print(a / b)
print(a ** 2)
print(a < b) #返回的将是一个布尔型数组
print(a > b) 
print(a.dot(b)) #点积。返回的是一个标量

• 数组特殊运算符

# dot, sum, min, max, cumsum
a = np.arange(10)

print(a.sum()) # >>>45
print(a.min()) # >>>0
print(a.max()) # >>>9
#返回一个新的一维数组，其中的元素为原数组的元素的累加和。如数组是[1, 2, 3]，新数组就是[1, 3, 6]
print(a.cumsum()) # >>>[ 0  1  3  6 10 15 21 28 36 45]

（3）索引进阶

• 花式索引

# Fancy indexing
a = np.arange(0, 100, 10)  # 步长为10
indices = [1, 5, -1] # index = 1， index = 5， 最后一个
b = a[indices]
print(a) # >>>[ 0 10 20 30 40 50 60 70 80 90]
print(b) # >>>[10 50 90]

• 布尔屏蔽

# Boolean masking
import matplotlib.pyplot as plt

a = np.linspace(0, 2 * np.pi, 50)
b = np.sin(a)
plt.plot(a,b)
mask = b >= 0
plt.plot(a[mask], b[mask], 'bo')
mask = (b >= 0) & (a <= np.pi / 2)
plt.plot(a[mask], b[mask], 'go')
plt.show()

• 缺省索引

#不完全索引是从多维数组的第一个维度获取索引或切片的一种方便方法
a = np.arange(0, 100, 10)
b = a[:5]
c = a[a >= 50]
print(b) # >>>[ 0 10 20 30 40]
print(c) # >>>[50 60 70 80 90]

• where函数

a = np.arange(0, 100, 10)
b = np.where(a < 50) 
c = np.where(a >= 50)[0]
print(b) # >>>(array([0, 1, 2, 3, 4]),)
print(c) # >>>[5 6 7 8 9]

1.2.numpy其他学习

• 其他numpy使用学习

2.pytorch 简单入门

为什么选择pytorch?

• 动态图，方便调试

PyTorch动态构建神经网络，执行到代码位置， 才开始构建这句代码所描述的网络节点， 然后把这一节点挂在计算图上。 可以让用户在动态改变神经网络时，不产生任何滞后和开销。它直观， 精简， 极度灵活。 缺点也非常明显，那就是运行效率和开销。

Tensorflow、Caffe都采用静态构建方式。用户需要先构建神经网络结构，然后在给定的结构上填入数据，再进行一次又一次的运行。能够对预先定义的网络进行多种优化处理，从而运行的更高效。但缺点也非常明显，即不够灵活，而且被优化后的网络，对用户不友好，调试时难以轻松知道程序的状态， 而且一旦用户想要根据计算的状态，动态的修改神经网络结构，那么实现起来会非常困难。

PyTorch这一工具的定位： 帮助科研人员和工程师， 快速探索和调整模型， 快速构建实验，更适合从0到1的创新工作， 而静态图Tensorflow，更适合已经有了模型， 我们要运用到某些高强度的训练和测试的应用环境下。更适合工业应用。

• pytorch官方教程

• pytorch官方文档

2.1.Pytorch的基本组成元素

PyTorch 四层抽象：

• Tensor: 基本数据单元，多维数组
• Variable：等同于带有梯度的Tensor
• nn: 卷积、池化、激活函数等层的实现
• Module: 网络结构，包含一系列Tensor和nn的计算过程

注意：在Pytorch > = 0.4版本中，将Variable与Tensor合并

Tensor：x = torch.ones(2, 2, requires_grad=False)
Variable：x = torch.ones(2, 2, requires_grad=True)

（1）Tensor

• 一些tensor操作函数

用于生成网络输入、输出、参数、中间变量等等

• 初始化：

torch.tensor((k*k*k…), dtype=torch.float)
torch.from_numpy(**)
torch.zero((k*k*k…)) # 初始化元素为0
torch.eye(k) # 初始化对角矩阵
torch.ones((k*k*k…)) # 初始化元素为1
torch.rand(k*k*k…) #随机初始化[0,1]
torch.randn(k*k*k…) #随机初始化, 0-均值 1-方差
data.cuda() #cpu转gpu

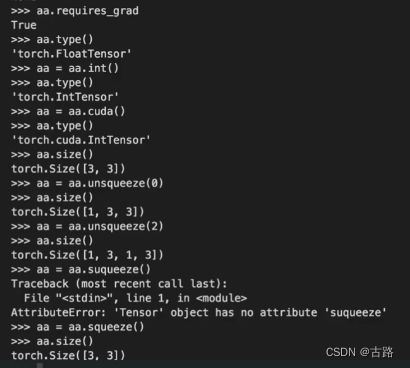
• 示例

• 其他的一些使用方法可以查询文档，注意带上torch版本号

• 基本运算

加减乘除：逐点操作
矩阵乘：data1.mm(data2)
数据维度：size(), reshape(), view(), squeeze, unsqueeze
转置：transpose，permute

（2）Tensor(requires_grad=True) <==>Variable

• tensor.data 获取数据
• tensor.grad 获取梯度
• tensor.grad_fn 获取产生方式

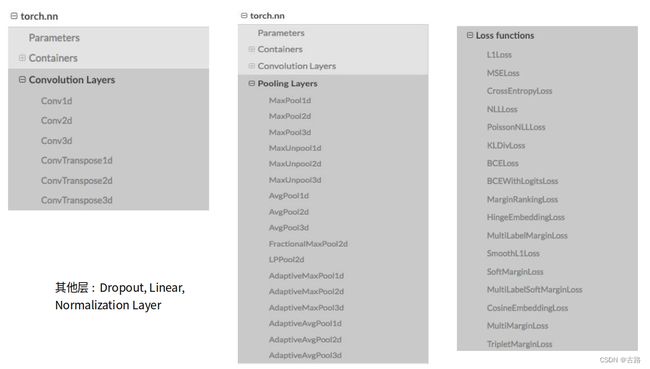
（3）nn-卷积.池化.激活等层

• 方式一：

• torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
• torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
• torch.nn.AvePool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
• torch.nn.ReLU(inplace=False)
• torch.nn.Sequential()

• 方式二：

• torch.nn.functional.conv2d(input, weight, bias=None, ward的过程中，Function和Variable组成了计算图，在backward时，只需调用Function的
backward就得到结果，因此Module不需要再定义backward。
• Module不仅包括了Function，还包括了对应的参数，以及其他函数与变量，这是Function所不具备的
• stride=1, padding=0, dilation=1, groups=1)
• torch.nn.functional.relu(input, inplace=False)

• 区别

• Function一般只定义一个操作，因为其无法保存参数，因此适用于激活函数、pooling等操作；Module是保存了参数，因此适合于定义一层，如线性层，
卷积层，也适用于定义一个网络
• Function需要定义三个方法：__init__, forward, backward（需要自己写求导公式）；Module：只需定义__init__和forward，而backward的计算由自动
求导机制构成
• Module是由一系列Function组成，因此其在for

---

• 方式一：

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
torch.nn.AvePool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
torch.nn.ReLU(inplace=False)
torch.nn.Sequential()

• 方式二：

torch.nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)
torch.nn.functional.relu(input, inplace=False)

区别:

• 方式一：

myConv = torch. nn.Conv2d(16, 33, 3, stride=1, padding=1)
myRelu = torch.nn.ReLU(inplace=True)
input = torch.randn(20, 16, 50, 100)
output = myConv(input)
output = myRelu(output)

• 方式二：

weight = torch.randn(33,16,3,3) 
input = torch.randn(20, 16, 50, 100)
output = torch.nn.functional.conv2d(input, weight,stride=1, padding=1)
output = torch.nn.functional.relu(output)

---

手写数字识别的torch版本：

import torch
N, D_in, H, D_out = 64, 1000, 100, 10
x = torch.randn((N, D_in), requires_grad=True)
y = torch.randn((N, D_out), requires_grad=False)
model = torch.nn.Sequential(torch.nn.Linear(D_in, H),
                           torch.nn.ReLU(),
                           torch.nn.Linear(H, D_out))
loss_fn = torch.nn.MSELoss(reduction='sum')

learning_rate = 1e-4
for t in range(500):
    y_pred = model(x)
    loss = loss_fn(y_pred, y)
    print(loss)
    
    model.zero_grad()
    loss.backward()
    for param in model.parameters():
        param.data -= learning_rate * param.grad.data

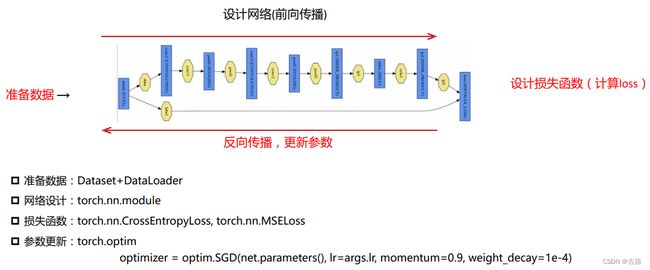
2.2.Pytorch构建神经网络

（1）Pytorch-数据准备

why use Dataset Dataloader？

• 可以快速、提前提取数据到内存中
• 提供框架，只需写核心函数
• 提供多种数据曾广支持

（2）module-神经网络

• Module 是 pytorch 提供的一个基类，每次我们要 搭建 自己的神经网络的时候都要继承这个类

• 主要函数：
  def init(self): #初始化网络所用的神经网络层
  def forward(self, x): #网络的前向过程
  def backward(self, x): #自动计算

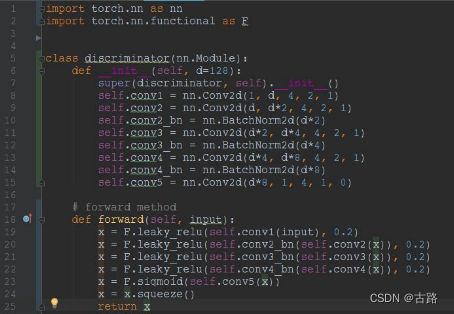
• 实例展示（lenet,vgg,resnet）

（3）网络模型

• 保存模型
• 加载训练好的模型

• 模型优化

• 学习率调整

2.3.进阶部分

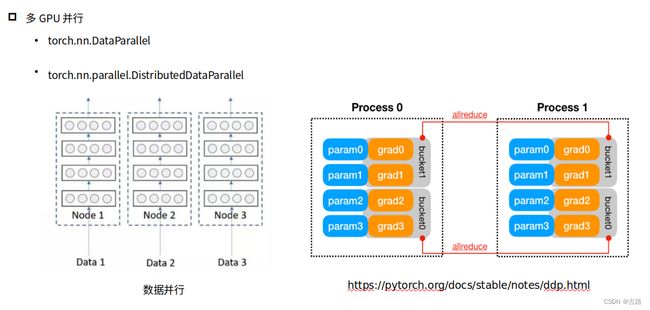
（1）多GPU并行

（2） cpp extension扩展

• 用途：

  • 实现新的功能，但是pytorch不支持
  • 代码运行速度有要求

• 途径—C拓展：

  • 准备.c文件实现
  • 利用工具编译为python可以调用的模块
  • 嵌入到pytorch网络中

（3） tensorboardX可视化

• 安装：

  • 安装tensorflow （cpu版本即可）
  • pip install tensorboardX

• 使用

  • 初始化：
    from tensorboardX import SummaryWriter
    writer = SummaryWriter('log‘)
  • 记录：
    writer.add_scalar(‘Train/Loss’, loss.data[0], niter)
    writer.add_scalar(‘Test/Accu’, correct/total, niter)
  • 可视化：
    tensorboard --logdir=./log
    http://0.0.0.0:6006/

ps：服务器必须和本机联网

• 参考

2.4.其他参考资料

• 固定部分网络参数

• C++拓展

• 不同层设置不同学习率

• tensorboardX可视化

• 其他注意事项：

  • 官方网站是最好最权威的学习网站
  • 问题搜索时注意带上pytorch版本号

其他学习链接：

• 知乎文章
• ref1
• PyTorch中文文档
• pytorch-tutorial
• 黄海广