深度强化学习方法:价值迭代法
目录
-
- 计算状态价值和动作价值步骤:
- 价值迭代方法实践
- Q-learning方法实践
计算状态价值和动作价值步骤:
以上只是结论,此方法有几个局限性:
1.他只限于状态空间是离散的问题,并且要足够小,才可以多次迭代
2.我们通常很少知道动作的转移概率:从s0采取a0到s1的概率是多少。也很少知道奖励矩阵
(我们只能够通过与环境互动的历史数据来推测这两个值,估计概率:为每个元组(a0,s1,a)维护一个计数器并标准化)
价值迭代方法实践
用于frozenlake游戏
奖励表:键:原状态+动作+目标状态 值:立即奖励
转移表:键:状态+动作 值:目标状态+次数
价值表:(V(s):是状态价值!!)对应计算出价值
导入包,设置参数和常量
#!/usr/bin/env python3此处根据自己环境改
import gym
import collections
from tensorboardX import SummaryWriter
ENV_NAME = "FrozenLake-v0"
#ENV_NAME = "FrozenLake8x8-v0" # uncomment for larger version
GAMMA = 0.9
TEST_EPISODES = 20
Agent类:
init函数创建了环境,获得了第一个s,定义了上面说到的表
接着就是定义了训练用到的函数:
play_n_random_steps中我们无需等到一个片段结束才能训练(向交叉熵方法一样,只能在完整的片段学习),而是执行N步并且记录了结果在表中就可以,这是价值迭代法与交叉熵方法的区别之一
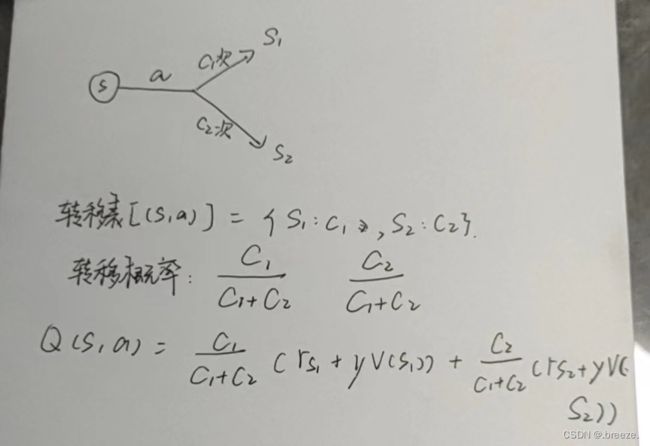
calc_action_value:用于计算价值,原理如下:
①转移表中获得(s,a)对应的下一状态对应的次数,求和后转变为转移概率
②对a所到达的每个s进行迭代,使用Bellman方程计算(立即奖励r+下一状态的折扣后的价值),再乘上转移概率(①算出来的)就是动作价值了Q(s,a)
 select_action:
select_action:
用于计算比较来决定最佳动作,做法是直接基于该状态s迭代所有的动作,进入calc_action_value函数去算,返回的Q最终取最大即可
play_episode:
在环境中运行一整个片段,此处为了不与play_n_random_steps中手收集探索信息的环境起冲突,所以另起环境。
value_iteration:处理价值表
该函数要做的只是对于每个s,能达到的每个a都计算Q,最后取最大的填入价值表即可
class Agent:
def __init__(self):
self.env = gym.make(ENV_NAME)
self.state = self.env.reset()
self.rewards = collections.defaultdict(float)
self.transits = collections.defaultdict(
collections.Counter)
self.values = collections.defaultdict(float)
def play_n_random_steps(self, count):#从环境中随机收集经验,更新奖励表和转移表
for _ in range(count):
action = self.env.action_space.sample()
new_state, reward, is_done, _ = self.env.step(action)
self.rewards[(self.state, action, new_state)] = reward
self.transits[(self.state, action)][new_state] += 1
self.state = self.env.reset() \
if is_done else new_state
def calc_action_value(self, state, action):
target_counts = self.transits[(state, action)]
total = sum(target_counts.values())
action_value = 0.0
for tgt_state, count in target_counts.items():
reward = self.rewards[(state, action, tgt_state)]
val = reward + GAMMA * self.values[tgt_state]
action_value += (count / total) * val
return action_value
def select_action(self, state):
best_action, best_value = None, None
for action in range(self.env.action_space.n):
action_value = self.calc_action_value(state, action)
if best_value is None or best_value < action_value:
best_value = action_value
best_action = action
return best_action
def play_episode(self, env):
total_reward = 0.0
state = env.reset()
while True:
action = self.select_action(state)
new_state, reward, is_done, _ = env.step(action)
self.rewards[(state, action, new_state)] = reward
self.transits[(state, action)][new_state] += 1
total_reward += reward
if is_done:
break
state = new_state
return total_reward
def value_iteration(self):
for state in range(self.env.observation_space.n):
state_values = [
self.calc_action_value(state, action)
for action in range(self.env.action_space.n)
]
self.values[state] = max(state_values)
if __name__ == "__main__":
test_env = gym.make(ENV_NAME)
agent = Agent()
writer = SummaryWriter(comment="-v-iteration")
iter_no = 0
best_reward = 0.0
while True:
iter_no += 1
agent.play_n_random_steps(100)#执行100个随即步骤,充分填充奖励表和转移表 (也充当了随即探索的任务)
agent.value_iteration()#运行价值迭代
reward = 0.0
for _ in range(TEST_EPISODES):
reward += agent.play_episode(test_env)
reward /= TEST_EPISODES
writer.add_scalar("reward", reward, iter_no)
if reward > best_reward:
print("Best reward updated %.3f -> %.3f" % (
best_reward, reward))
best_reward = reward
if reward > 0.80:
Q-learning方法实践
与前面的区别在于此处的价值表有两个参数 s 和a
求的是Q(s,a)
并且不需要calc_action_value函数了,因为价值表里面存的就是动作价值
value_iteration函数需要稍作更改,但是原理差不多,就是按照公式,根据bellman方程计算状态的值
def value_iteration(self):
for state in range(self.env.observation_space.n):
for action in range(self.env.action_space.n):
action_value = 0.0
target_counts = self.transits[(state, action)]
total = sum(target_counts.values())
for tgt_state, count in target_counts.items():
key = (state, action, tgt_state)
reward = self.rewards[key]
best_action = self.select_action(tgt_state)
val = reward + GAMMA * \
self.values[(tgt_state, best_action)]
action_value += (count / total) * val
self.values[(state, action)] = action_value
在select_action里面也是,直接查就好,不需要calc_action_value函数
def select_action(self, state):
best_action, best_value = None, None
for action in range(self.env.action_space.n):
action_value = self.values[(state, action)]
if best_value is None or best_value < action_value:
best_value = action_value
best_action = action
return best_action
这样做的好处在于,其实calc_action_value里面用到了概率和奖励信息,在这里没有太大的影响因为训练过程中依赖此信息。对于一些概率不需要近似而是直接从环境样本中需得到的情况,这样会加重智能体负担,而Q-learning中只依赖于价值表所做的决定,所以在价值学习领域,Q-learning更受欢迎。