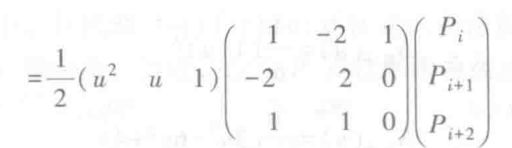【12月学习进度9/31——计算机图形学期末准备06】四阶三次B样条曲线矩阵形式推导及MATLAB实现
B样条曲线的递归定义

B样条曲线与给定的阶数 k k k 和 节点向量都有关
↓
即使选取的阶数 k k k 相同,但节点向量不同,则得到的曲线也不同
一些规律:

递推图示:
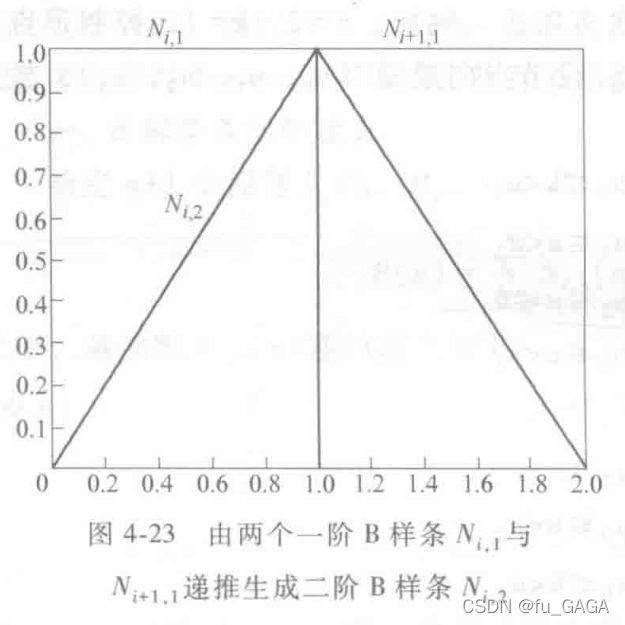


k k k 阶B样条 N i , k ( u ) N_{i,k}(u) Ni,k(u) 可由两个 k − 1 k-1 k−1 阶 N i , k − 1 ( u ) , N i + 1 , k − 1 ( u ) N_{i,k-1}(u),N_{i+1,k-1}(u) Ni,k−1(u),Ni+1,k−1(u) 递推得到
系数的含义:
系数分别为
u − u i u i + k − 1 − u i \frac{u-u_i}{u_{i+k-1}-u_i} ui+k−1−uiu−ui
和
u i + k − u i u i + k − u i + 1 \frac{u_{i+k}-u_i}{u_{i+k}-u_{i+1}} ui+k−ui+1ui+k−ui
分母分别为两个 k − 1 k-1 k−1 阶基函数的支撑区间:
- N i , k − 1 ( u ) N_{i,k-1}(u) Ni,k−1(u) 的支撑区间为 [ u i , u i + k − 1 ) [u_i,u_{i+k-1}) [ui,ui+k−1)
- N i + 1 , k − 1 ( u ) N_{i+1,k-1}(u) Ni+1,k−1(u) 的支撑区间为 [ u i + 1 , u i + k ) [u_{i+1},u_{i+k}) [ui+1,ui+k)
分子为参数 u u u 将 N i , k ( u ) N_{i,k}(u) Ni,k(u) 的支撑区间 [ u i , u i + k ) [u_i,u_{i+k}) [ui,ui+k) 划分为两部分
- u − u i {u-u_i} u−ui 为参数 u u u 距离左端节点位置
- u i + k − u {u_{i+k}-u} ui+k−u 为参数 u u u 距离右端节点位置
分子(距离)除以分母(区间长度)后,将距离归一化到 ( 0 , 1 ) (0,1) (0,1) 之间
因此, N i , p ( u ) N_{i,p}(u) Ni,p(u) 是 N i , p − 1 ( u ) N_{i,p-1}(u) Ni,p−1(u) 和 N i + 1 , p − 1 ( u ) N_{i+1,p-1}(u) Ni+1,p−1(u) 的线性组合,有两个系数,都在 u u u 上是线性的,在0和1之间。
四阶均匀B样条曲线
1.计算四阶B样条基函数 N i , 4 ( u ) N_{i,4}(u) Ni,4(u)
根据递推公式计算:



如上图所示,B样条基函数 N i , 4 ( u ) N_{i,4}(u) Ni,4(u) 由四段三次多项式曲线拼接而成。
四条三次多项式曲线如下图所示:
(分别为实线、虚线、点线、点划线)

其中B样条基函数 N i , 4 ( u ) N_{i,4}(u) Ni,4(u) 曲线为下图中红色曲线:
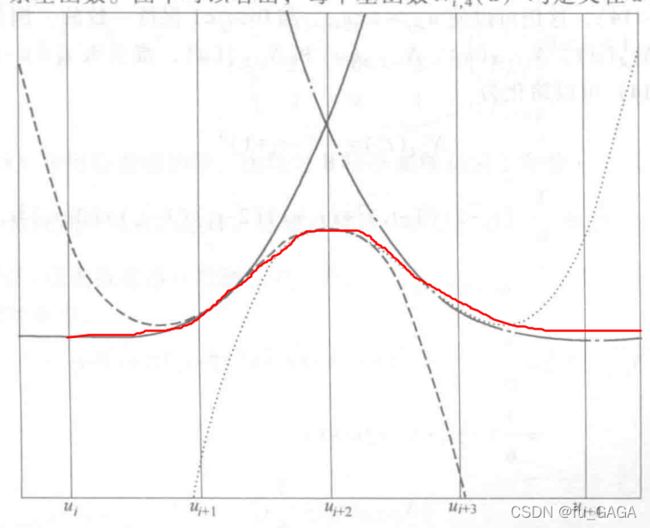
均匀B样条基函数在曲线定义域内各个节点区间上都有相同图形
(相同公式,其中所有的 u i + 1 − u i u_{i+1}-u_i ui+1−ui 都相同)
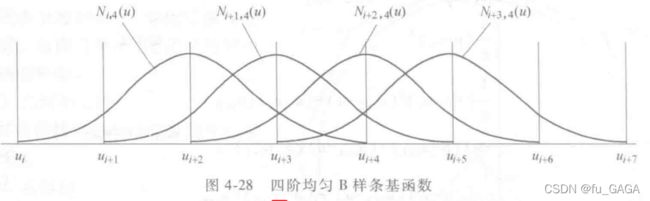
上图可以分析B样条的局部控制特性
例:
第一个控制点 P i P_i Pi 只与 N i , 4 ( u ) N_{i,4}(u) Ni,4(u) 相乘(由B样条曲线定义式得),所以其影响 N i , 4 ( u ) N_{i,4}(u) Ni,4(u) 的支撑区间 ( u i , u i + 4 ) (u_i,u_{i+4}) (ui,ui+4) 上的曲线的形状
2. 简化函数形式
以其中一个节点区间 [ u i + 3 , u i + 4 ) [u_{i+3},u_{i+4}) [ui+3,ui+4) 为例:

上图中 ( i , j ) (i,j) (i,j) 表示第 i i i 个基函数的第 j j j 段分片

上述公式中很多 u − u i + j u-u_{i+j} u−ui+j 形式的因子
↓
↓ 令 t j = u − u i + j t_j = u-u_{i+j} tj=u−ui+j
↓
(仍以区间 [ u i + 3 , u i + 4 ) [u_{i+3},u_{i+4}) [ui+3,ui+4) 为例)
引入
t 3 = u − u i + 3 t_3 = u-u_{i+3} t3=u−ui+3
则
u i + j ≤ u < u i + j + 1 < = > 0 ≤ t j < 1 u_{i+j} ≤ u < u_{i+j+1} <=> 0≤t_j<1 ui+j≤u<ui+j+1<=>0≤tj<1
(注: ( u i , u i + 1 , . . . , u i + k ) (u_i,u_{i+1},...,u_{i+k}) (ui,ui+1,...,ui+k)是间隔为1的节点向量)

上述式子对任意的 i i i 均成立
令 i = 0 i=0 i=0 , t 3 t_3 t3 用 u u u 名称替换,得如下:


每4个点一组,确定一段三次曲线
【矩阵形式表示】

同理可得,
二阶一次B样条曲线表达式:

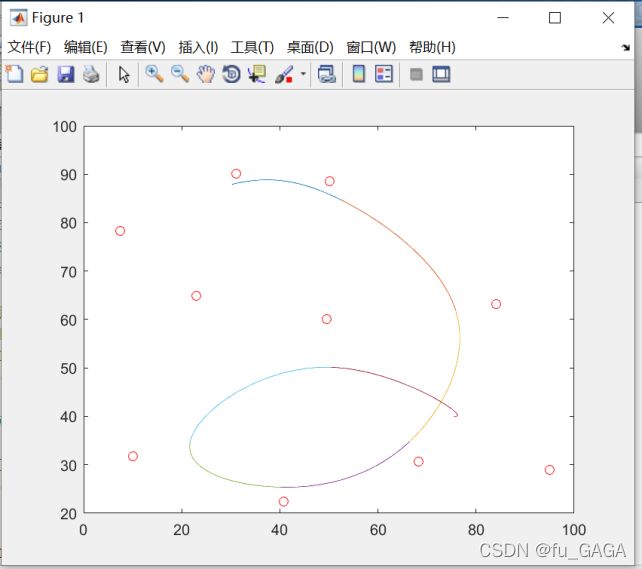
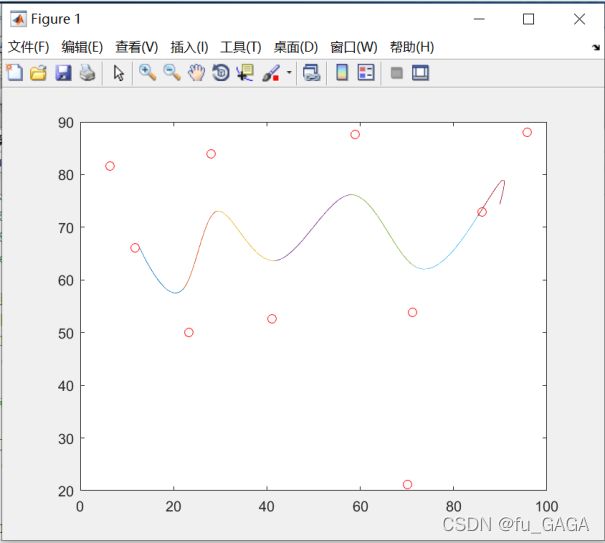
四阶三次B样条曲线MATLAB实现
利用四阶三次的矩阵形式实现
依次计算每一段曲线的x,y坐标,并存入2个结果矩阵 x x , y y xx,yy xx,yy
x x xx xx 矩阵每一行为每一段曲线对应的所有 x x x 坐标
y y yy yy 矩阵每一行为每一段曲线对应的所有 y y y 坐标
byang.m函数文件 :
function byang(n)
%输入n个点
axis([0,100,0,100]) %定义画布大小
[px,py] = ginput(n);
plot(px,py,'ro');
hold on;
xx=[];
yy=[];%用来存储B样条的x,y值
for i=1:n-3
%每一个i对应于一段曲线
x_temp = [];
y_temp = [];
for u = 0:0.01:1
x_item = (1/6)*[u^3,u^2,u,1]*[-1,3,-3,1;3,-6,3,0;-3,0,3,0;1,4,1,0]*[px(i);px(i+1);px(i+2);px(i+3)];
y_item = (1/6)*[u^3,u^2,u,1]*[-1,3,-3,1;3,-6,3,0;-3,0,3,0;1,4,1,0]*[py(i);py(i+1);py(i+2);py(i+3)];
x_temp=[x_temp,x_item];
y_temp=[y_temp,y_item];%保存当前u对应的x,y值
end
%绘制完该条曲线
%每条曲线对应于xx,yy的一行
xx = [xx;x_temp];
yy = [yy;y_temp];
end
[i,j] = size(xx);
for k = 1:i %i为行数
plot(xx(k,:),yy(k,:));%画出每一段曲线
end
使用ginput函数,获取用户选中的点的坐标:
结果: