均匀B样条和准均匀B样条

均匀B样条拟合和准均匀B样条拟合

在CAGD中最为重要的无非就是B样条曲线，B样条在保留Bezier曲线优点的同时，克服了其由于整体表示带来不具有局部性质的缺点，以及解决了在描述复杂形状时带来的连接问题。B样条曲线按照节点矢量中节点的分布情况不同，可划分为如下4种类型：(a)均匀B样条曲线;
(b)准均匀B样条曲线;
©分段Bezier曲线;
(d)一般非均匀B样条曲线。

均匀B样条

(1) 对于均匀B样条曲线，其方程的矩阵表达形式为：

其中系数M_k(k=1,2,3)分别为：

使用系数矩阵能大大的简化参数曲线基函数的计算。带入不同的阶数的矩阵即可得到相应的次数的均匀B样条曲线。关于系数矩阵的推导，更为直观的是一种基于几何特性的三次均匀B样条曲线构造描述，该方法更为直观的描述了三次均匀B样条曲线构造的原理和过程，给出了不同曲线段情况下曲线特征构造和插值构造的相关公式。

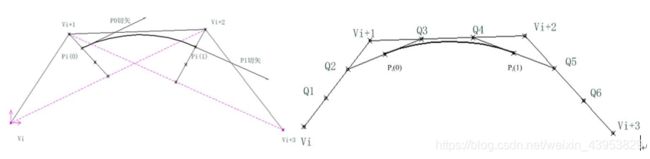
图(a)是常见的三次均匀B样条曲线段的几何表示方法，图(b)是通过分析a所表达的曲线的性质得到的与图a等价的几何表示。在图b中，将定义该线段的4个特征点所构成的特征多边形的3条边均3等分，Q₁-Q₆即为对应的等分点，连接Q₂Q₃、Q₄Q₅则此连线的中点分别为曲线段的起点P_i(0)和终点P_i(1)，且曲线段首末端点切矢分别为Q₂Q₃、Q₄Q₅。由特征点V_i、V_i+1、V_i+2、V_i+3定义的一段三次均匀B样条曲线段等价于由点P_i(0)、Q₃、Q₄、P_i(1)所定义的一段三次Bezier曲线。

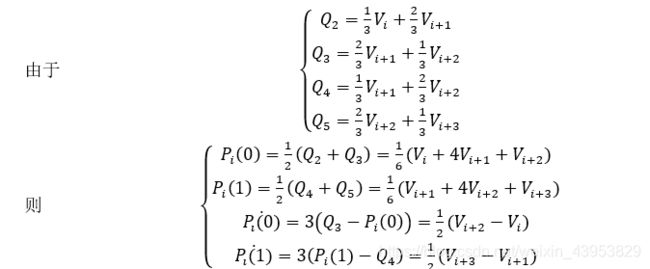
由上式可以看出，只要得到对应的Bezier点，即可方便的得出各段曲线的数学表达式。另一种数学方式可以将系数基矩阵M显式表达即为：

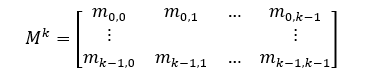
其中m_ij可以依照下式计算得出：

例如在k=4时，求得三次均匀B样条基的系数矩阵为：

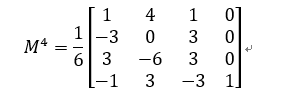
准均匀B样条曲线拟合

对于准均匀B样条，其原理也是利用特征控制点对应的Bezier曲线分段，基于对推定义和四重节点端点条件，准均匀B样条曲线矩阵形式数学表达式课变换如下形式：

由式(22)可以看出，三次准均匀B样条曲线的求取关键是基的系数矩阵M的求取，相较于均匀B样条曲线，区别在于首末两段Bezier曲线。下面进行M_k的推导：由给定的控制点可知曲线段数n>6，则对于前两段和末尾两段曲线均存在四重节点。对于中间段的系数矩阵MK与三次均匀B样条的基系数矩阵相同即为

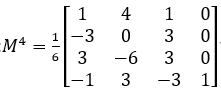
该矩阵也可以通过几何特性得到，结果一致，如下图

对于矩阵的推导在这里就不赘述了，我们只需要了解是怎么推导出来的，并且了解如何使用即可，准均匀B样条曲线与均匀B样条曲线所存在的区别，只要在与首末攻4段曲线，当曲线段数大于6时，要注意基的系数矩阵的使用，下面给出准均匀B样条基的系数矩阵：

将上述矩阵带入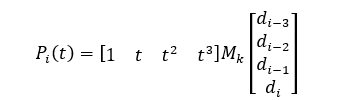即可前两段曲线的表达式，同理末尾两端曲线的基的系数矩阵为：

利用Matlab对上述矩阵进行验证，已知在AUTOCAD电子图板依据几何作图的方式16个特征控制点所得的三次准均匀B样条曲线如下图所示：


为了验证算法准确性，取得点较为简单，旨在验证数值方法和几何作图法做准均匀B样条。

对比分析可知，所得结果一致。通过不同的方式能够的到相同的结果，这正是B样条曲线令人着迷的地方，B样条曲线的产生与发展是工程实际与数学理论高度写作融合所得的结晶。
一下代码为上述过程的实现，代码较为粗糙，目的为了验证，未作修改由18个控制点求B样条曲线

clear;
flag=1;
for t=0:0.05:1;
% t=1;
hold on
d0=[0 0 ];
d1=[10 10];
d2=[20 10];
d3=[30 0];
d4=[40 0];d5=[50 10];d6=[60 10];d7=[70 0];d8=[80 0];d9=[90 10];
d10=[100 -10];d11=[90 -20];d12=[80 -20];d13=[70 -10];d14=[60 -10];
d15=[50 -20];d16=[40 -20];d17=[30 -10];
m=[0 10 20 30 40 50 60 70 80 90 100 90 80 70 60 50 40 30];
n=[0 10 10 0 0 10 10 0 0 10 -10 -20 -20 -10 -10 -20 -20 -10];
D=[d0;d1;d2;d3];
D2=[d1;d2;d3;d4];
D3=[d2;d3;d4;d5];
D4=[d3;d4;d5;d6];
D5=[d4;d5;d6;d7];
D6=[d5;d6;d7;d8];
D7=[d6;d7;d8;d9];
D8=[d7;d8;d9;d10];
D9=[d8;d9;d10;d11];
D10=[d9;d10;d11;d12];
D11=[d10;d11;d12;d13];
D12=[d11;d12;d13;d14];
D13=[d12;d13;d14;d15];
D14=[d13;d14;d15;d16];
D15=[d14;d15;d16;d17];
M1=[-1,7/4,-11/12,1/6;3,-9/2,3/2,0;-3,3,0,0;1,0,0,0];
M2=[-1/4,7/12,-1/2,1/6;3/4,-5/4,1/2,0;-3/4,1/4,1/2,0;1/4,7/12,1/6,0];
M3=[-1/6,1/2,-1/2,1/6;1/2,-1,1/2,0;-1/2,0,1/2,0;1/6,2/3,1/6,0];
M4=[-1/6,1/2,-1/2,1/6;1/2,-1,1/2,0;-1/2,0,1/2,0;1/6,2/3,1/6,0];
M5=[-1/6,1/2,-1/2,1/6;1/2,-1,1/2,0;-1/2,0,1/2,0;1/6,2/3,1/6,0];
M6=[-1/6 1/2 -7/12 1/4;1/2 -1 1/2 0;-1/2 0 1/2 0;1/6 2/3 1/6 0];
M7=[-1/6 11/12 -7/4 1;1/2 -5/4 3/4 0;-1/2 -1/4 3/4 0;1/6 7/12 1/4 0];
pt1=[t.^3,t.^2,t,1]*M1*D;
pt2=[t.^3,t.^2,t,1]*M2*D2;
pt3=[t.^3,t.^2,t,1]*M3*D3;
pt4=[t.^3,t.^2,t,1]*M4*D4;
pt5=[t.^3,t.^2,t,1]*M5*D5;
pt6=[t.^3,t.^2,t,1]*M5*D6;
pt7=[t.^3,t.^2,t,1]*M5*D7;
pt8=[t.^3,t.^2,t,1]*M5*D8;
pt9=[t.^3,t.^2,t,1]*M5*D9;
pt10=[t.^3,t.^2,t,1]*M5*D10;
pt11=[t.^3,t.^2,t,1]*M5*D11;
pt12=[t.^3,t.^2,t,1]*M5*D12;
pt13=[t.^3,t.^2,t,1]*M5*D13;
pt14=[t.^3,t.^2,t,1]*M6*D14;
pt15=[t.^3,t.^2,t,1]*M7*D15;
px(flag)=pt1(1);py(flag)=pt1(2);
px2(flag)=pt2(1);py2(flag)=pt2(2);
px3(flag)=pt3(1);py3(flag)=pt3(2);
px4(flag)=pt4(1);py4(flag)=pt4(2);
px5(flag)=pt5(1);py5(flag)=pt5(2);
px6(flag)=pt6(1);py6(flag)=pt6(2);
px7(flag)=pt7(1);py7(flag)=pt7(2);
px8(flag)=pt8(1);py8(flag)=pt8(2);
px9(flag)=pt9(1);py9(flag)=pt9(2);
px10(flag)=pt10(1);py10(flag)=pt10(2);
px11(flag)=pt11(1);py11(flag)=pt11(2);
px12(flag)=pt12(1);py12(flag)=pt12(2);
px13(flag)=pt13(1);py13(flag)=pt13(2);
px14(flag)=pt14(1);py14(flag)=pt14(2);
px15(flag)=pt15(1);py15(flag)=pt15(2);
flag=flag+1;
x2=px2;y2=py2;
x3=px3;y3=py3;
x4=px4;y4=py4;
x5=px5;y5=py5;
x6=px6;y6=py6;
x7=px7;y7=py7;
x8=px8;y8=py8;
x9=px9;y9=py9;
x10=px10;y10=py10;
x11=px11;y11=py11;
x12=px12;y12=py12;
x13=px13;y13=py13;
x14=px14;y14=py14;
x15=px15;y15=py15;
x=px;y=py;
plot (x,y,'r.');
plot (x2,y2,'r.');
plot (x3,y3,'r.');
plot (x4,y4,'r.');
plot (x5,y5,'r.');
plot (x6,y6,'r.');
plot (x7,y7,'r.');
plot (x8,y8,'r.');
plot (x9,y9,'r.');
plot (x10,y10,'r.');
plot (x11,y11,'r.');
plot (x12,y12,'r.');
plot (x13,y13,'r.');
plot (x14,y14,'r.');
plot (x15,y15,'r.');
plot (m,n,'b--');
axis equal;
xlabel('X(mm)');
ylabel('Y(mm)');
end

由于笔者刚开始接触Matlab时，还不熟练，又因点数较少，因此用枚举法写的程序哈哈哈哈哈，见笑了，当然后面已经有了很大改善。
例如由插值点反求控制点如下：

红色点为插值点，由曲线上的插值点，反求出控制点，与上述控制点求取插值点结果重合，表明正确。
具体知识理论以及代码，后续更新。