机器学习模型评估标准及sklearn实现方法
目录
- 分类模型评估标准
-
- 错误率与精度(accuracy)
- 查准率(precision)、查全率(recall)与F1-score
- ROC曲线、AUC
- log-loss
- 回归模型评估
-
- 平均绝对误差(MAE)
- 平均平方误差(MSE)
- 均方根误差(RMSE)
- R-squared
分类模型评估标准
错误率与精度(accuracy)
错误率和精度是分类任务中最常用的两种性能度量,既适用于二分类任务,也适用于多分类任务。错误率是分类错误的样本数占样本总数的比例,精度则是分类正确的样本数占样本总数的比例。
from sklearn import metrics
print('模型精度:',metrics.accuracy_score(y_test,y_predict))
查准率(precision)、查全率(recall)与F1-score
对于二分类问题,可将样例根据其真实类别与学习器预测类别的组合划分为真正例(true positive) 、假正例(false positive) 、真反例(true negative) 、假反例(false negative) 四种情形,令TP 、FP 、TN 、FN 分别表示其对应的样例数,则显然有TP+FP+TN+FN=样例总数。
正例(Positives):你所关注的识别目标就是正例。
负例(Negatives):正例以外的就是负例。
TP: 如果一个实例是正类并且也被预测成正类,即为真正类(True Positive)。
FP: 如果一个实例是负类而被预测成正类,即为假正类(False Positive)。
TN: 如果一个实例是负类并且也被预测成负类,即为真负类(True Negative)。
FN: 如果一个实例是正类而被预测成负类,即为假负类(False Negative)。
分类结果的"混淆矩阵" (confusion matrix) 如下表所示:

查准率(P值)是针对我们的预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。
查全率(R值)是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。
查准率 P与查全率 R 分别定义为:
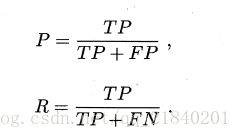
一般来说,查准率高时,查全率往往偏低;而查全率高时,查准率往往偏低。
F1-score是统计学中用来衡量二分类模型精确度的一种指标。它同时兼顾了分类模型的准确率和召回率。F1分数可以看作是模型准确率和召回率的一种加权平均,它的最大值是1,最小值是0。
随着阈值的变化,就像假设检验的两类错误一样,如下图所示召回率和精确率不能同时提高,因此我们就需要一个指标来调和这两个指标,于是人们就常用F1-score来进行表示:

print('查准率:',metrics.precision(y_test,y_predict,average='micro'))
print('查全率:',metrics.recall_score(y_test,y_predict,average='micro'))
print('F1-score:',metrics.precision_score(y_test,y_predict,average='micro'))
average参数定义了该指标的计算方法,二分类时average参数默认是binary;多分类时,可选参数有micro、macro、weighted和samples。
None:返回每个分类的分数。否则,这将确定对数据执行的平均类型。
binary:仅报告由指定的类的结果pos_label。仅当targets(y_{true,pred})是二进制时才适用。
micro:通过计算总真阳性,假阴性和误报来全球计算指标。也就是把所有的类放在一起算(具体到precision),然后把所有类的TP加和,再除以所有类的TP和FN的加和。因此micro方法下的precision和recall都等于accuracy。
macro:计算每个标签的指标,找出它们的未加权平均值。这不会考虑标签不平衡。也就是先分别求出每个类的precision再求其算术平均。
weighted:计算每个标签的指标,并找到它们的平均值,按支持加权(每个标签的真实实例数)。这会改变“宏观”以解决标签不平衡问题; 它可能导致F分数不在精确度和召回之间。
samples:计算每个实例的指标,并找出它们的平均值(仅对于不同的多标记分类有意义 accuracy_score)。
ROC曲线、AUC
ROC(Receiver Operating Characteristic) 受试者工作特征曲线的纵轴是"真正例率" (True Positive Rate,简称TPR) ,也称灵敏度,横轴是"假正例率" (False Positive Rate,简称FPR) ,也称1-特异度,两者分别定义为:

下面给出ROC曲线示意图:
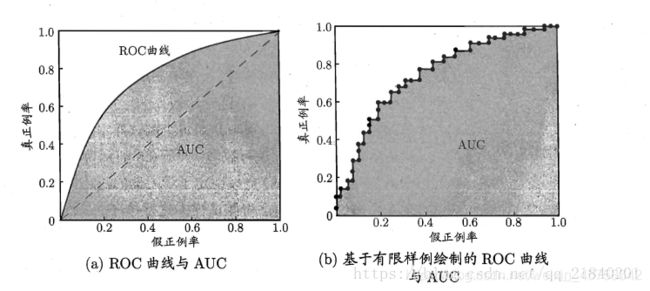
现实任务中通常是利用有限个测试样例来绘制ROC图,此时仅能获得有限个(真正例率,假正例率)坐标对,无法产生图 (a) 中的光滑ROC 曲线, 只能绘制出如图 (b) 所示的近似ROC 曲线。
AUC的全称是(Area Under then Curve Of ROC), 十分直白就是ROC曲线下方的面积,AUC的值越大越好,其取值范围为(0.5,1)。
log-loss
很多机器学习的算法通常会用log-loss作为模型评价的指标,对数损失(Log loss)亦被称为逻辑回归损失(Logistic regression loss)或交叉熵损失(Cross-entropy loss),简单来说就是逻辑回归的损失函数。Logloss的公式如下:

其中y为预测值,N为样本数,p为预测概率。
y_pred=LR.(predict_proba(X))[:,1]预测类别为1的概率
print('log-loss:',metrics.log_loss(y_test,y_pred))
回归模型评估
平均绝对误差(MAE)
平均绝对误差MAE(Mean Absolute Error)又被称为L1。范围是0到正无穷,误差越大,MSE越大。

平均平方误差(MSE)
平均平方误差MSE(Mean Squared Error)又被称为L2。范围是0到正无穷,误差越大,MSE越大。

均方根误差(RMSE)
RMSE虽然广为使用,但是其存在一些缺点,因为它是使用平均误差,而平均值对异常点(outliers)较敏感,如果回归器对某个点的回归值很不理性,那么它的误差则较大,从而会对RMSE的值有较大影响,即平均值是非鲁棒的。范围是0到正无穷,误差越大,RMSE越大。

R-squared
R方介于0~1之间,越接近1,回归拟合效果越好,一般认为超过0.8的模型拟合优度比较高。
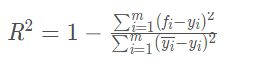
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
# MSE
mse_predict = mean_squared_error(y_test, y_predict)
# MAE
mae_predict = mean_absolute_error(y_test, y_predict)
# RMSE
np.sqrt(mean_squared_error(y_test,y_predict)) # RMSE就是对MSE开方即可
# R方
R2_predict = r2_score(y_test,y_predict)
# y_test:测试数据集中的真实值
# y_predict:根据测试集中的x所预测到的数值