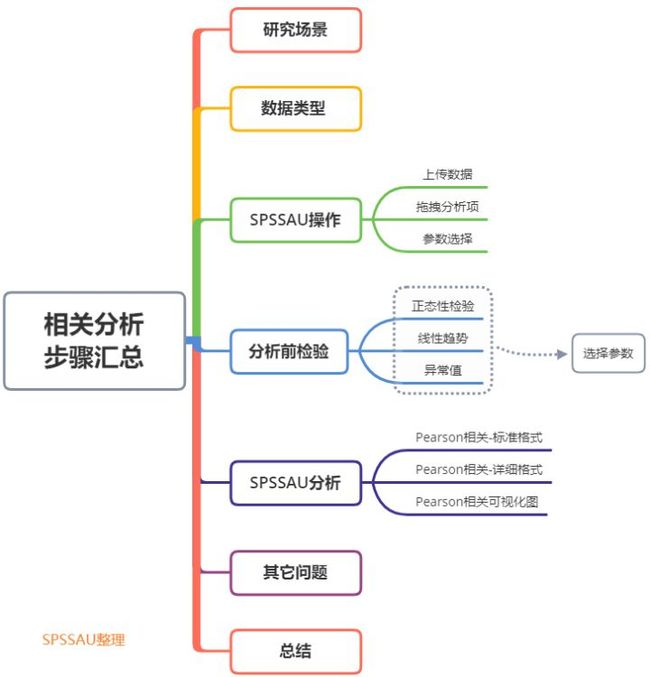
相关分析怎么进行？有哪些条件？

一、研究场景

相关分析用于研究定量数据之间的关系情况，包括是否有关系,以及关系紧密程度等。例如：研究员工薪资与员工工龄的关系；产品销量与产品售后服务的关系等。

二、数据类型

相关分析的适用范围很广，理论上讲，凡是考察两个变量相关性，都可以叫做相关分析。相关分析研究是定量与定量的数据，如果是定类和定量数据需要使用方差分析，定类和定类需要使用交叉（卡方）。

三、SPSSAU操作

1.上传数据

登录账号后进入SPSSAU页面，点击右上角“上传数据”，将处理好的数据进行“点击上传文件”上传即可。

2.拖拽分析项

在“通用方法”模块中选择“相关”方法，将分析项定量变量放于分析框内，点击“开始分析”即可。

3.参数选择

SPSSAU在相关分析中提供

四、分析前检验

1.正态性检验

相关分析要求数据服从正态分布，因此分析前需要检验数据的正态性。正态性有多种检验方法，常见方法如：正态图、正态性检验、P-P图/Q-Q图等。

补充说明：相关分析对数据正态要求比较宽松，违反时系数计算结果也比较稳健，只要数据基本满足正态即可。如果数据完全不正态，则可以用Spearman相关系数。

2.线性趋势

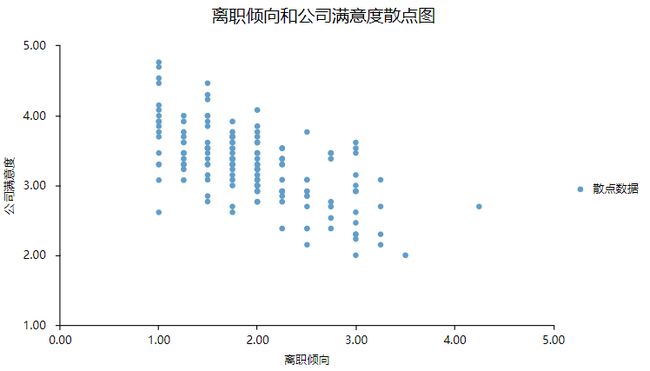
当两个定量数据在散点图上的散点呈现直线趋势时，就可以认为两者存在直线相关趋势，这也是相关分析的一个基本前提。

补充说明：可使用SPSSAU中可视化下的散点图进行分析与查看。

例如上图，当X增大时，可以比较明显地看出Y会随着减小，说明X和Y之间有着负向相关关系。如果是正相关，散点图会呈现随着一个变量值的增加，另一个变量值也增加的趋势。

如果数据呈现非线性的趋势，可以选择对变量进行数据转换（如对数转换），或是使用Spearman相关系数进行分析。

3.异常值

相关分析对极端值较为敏感，异常值会影响分析结果。需要在分析前查看是否存在异常值，保证结果的可靠性，此步可以和上一步一起通过散点图查看。

如果存在异常值，可以使用SPSSAU数据处理里面的异常值进行处理。

五、SPSSAU分析

1.Pearson相关-标准格式

从上表可知，利用相关分析去研究公司满意度和人际关系, 机会感知, 离职倾向, 工作条件共4项之间的相关关系，使用Pearson相关系数去表示相关关系的强弱情况。

其中上表展示了各个变量的均值标准差以及相关系数等，例如：公司满意度的平均值为3.291，标准差为0.541，人际关系的平均值是3.748，标准差为0.616，机会感知的平均值3.322以及标准差为0.602，以此类推。

补充说明：对于相关分析，一般规范的表格格式是：p 值使用*号表示（标识在相关系数的右上角），p < 0.01使用2个*号表示；p < 0.05使用1个*号表示。同时 SPSSAU也提供一个带具体p 值的结果表格。

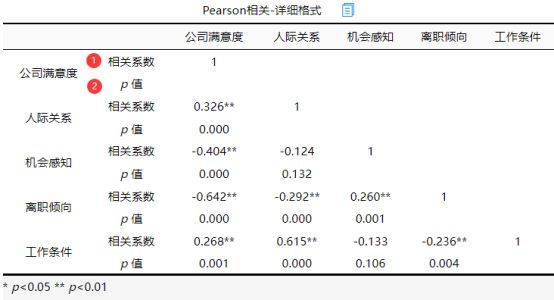
2.Pearson相关-详细格式

具体来看，公司满意度和人际关系之间的相关系数值为0.326，并且呈现出0.01水平的显著性，因而说明公司满意度和人际关系之间有着显著的正相关关系。

公司满意度和机会感知之间的相关系数值为-0.404，并且呈现出0.01水平的显著性，因而说明公司满意度和机会感知之间有着显著的负相关关系。

公司满意度和离职倾向之间的相关系数值为-0.642，并且呈现出0.01水平的显著性，因而说明公司满意度和离职倾向之间有着显著的负相关关系。

公司满意度和工作条件之间的相关系数值为0.268，并且呈现出0.01水平的显著性，因而说明公司满意度和工作条件之间有着显著的正相关关系。

补充说明：详细格式针对于标准格式输出了p值，当然标准格式含有每个分析项的平均值和标准差。

3.Pearson相关可视化图

可直观的看到分析项之间的相关系数，例如：公司满意度与人际关系的相关系数为0.33，公司满意度与机会感知的相关系数为-0.40以此类推，另外SPSSAU还提供了不同取值范围颜色深浅不同这一特征。

六、其它问题

1.针对问卷量表数据，几个题表示一个维度，如何处理？

比如有两个题“我愿意向朋友推荐SPSSAU”，“我有需要会再来使用SPSSAU”，此两个题是“忠诚度”的体现。但现在需要“忠诚度”这个整体，而不是具体两个标题，此时如何办呢？

2.相关分析不正态时如何办？

理论上讲，如果数据正态分布时，可使用Pearson相关系数进行相关分析；如果数据不正态时，则使用Spearman相关系数进行相关分析。但理论上的正态分布基本没有，只要数据非正态情况在可接受范围内则可继续使用Pearson系数；

而且一般情况下Pearson和Spearman系数的结论基本保持一致。所以绝大多数研究均是使用Pearson相关系数，而较少使用Spearman相关系数。

七、总结

以上就是相关分析的分析流程梳理。理论上都应该按照上述步骤进行分析，但在实际过程中，即使忽略其中的步骤，也能得到稳定的结果。

因此即使不按照步骤分析，也没有问题，而对于没有分析经验的研究者，SPSSAU建议按提供的步骤进行分析，才是最保险的做法。

---

以上就是相关分析步骤汇总，更多干货登录SPSSAU官网了解更多。