假设检验——Z检验、t检验
假设检验,也称为显著性检验,通过样本的统计量来判断与总体参数之间是否存在差异(差异是否显著)。即我们对总体参数进行一定的假设,然后通过收集到的数据,来验证我们之前作出的假设(总体参数)是否合理。在假设检验中,我们会建立两个完全对立的假设,分别为原假设H0与备择假设H1。然后根据样本信息进行分析判断,是选择接受原假设还是拒绝原假设。
假设检验基于“反证法”。首先,我们假设原假设为真,如果在此基础上,得出了违反逻辑与常理的结论,则表明原假设是错误的,我们就接受备择假设。
小概率事件
在假设检验中,违反逻辑与常规的结论,就是小概率事件。一般来说,小概率事件在一次试验中是不会发生的。如果发生,则我们便有理由拒绝原假设。
假设检验遵循“疑罪从无”的原则,接受原假设,并不代表原假设一定是正确的,只是没有充分的证据,证明原假设是错误的。
P-Value与显著性水平
为了便于量化,我们可以计算一个概率值(P-Value),该概率值可以认为是支持原假设的概率,也就是样本统计量与总体参数无差异的概率。然后,我们设定一个显著性水平α(通常取值为0.05)。当P-Value的值大于α时,支持原假设。
假设检验与置信区间有一定的关联性,只不过假设检验是通过反正的角度来判断是否接受原假设。
假设检验的步骤
步骤如下:
- 设置原假设与备择假设。
- 设置显著性水平α(通常选择α=0.05)。
- 根据问题选择假设检验的方式。
- 计算统计量,并通过统计量获取P值。
- 根据P值与α值,决定接受原假设还是备择假设。
常用的假设检验方法
Z检验
Z检验用来判断样本均值是否与总体均值具有显著性差异。Z检验是通过正态分布的理论来推断差异发生的概率,从而比较两个均值的差异是否显著。Z检验适用于:
- 总体呈正态分布。
- 总体方差已知。
- 样本容量较大(≥30)。
Z检验计算公式如下:

通过假设检验可以计算如下题目:
某车间用一台机器制作袋装糖,袋装糖的净重是一个随机变量,服从正态分布。机器运行正常时,其均值为0.5kg,标准差为0.015kg。某日工作后,检验包装机是否正常,随机抽取9袋糖,称得净重为(kg):0.497、0.506、0.518、0.524、0.498、0.511、0.520、0.515、0.512,请问机器是否正常?
- 设置原假设与备择假设:
原假设:μ = μ0 = 0.5kg(机器正常)
备择假设:μ ≠ μ0 ≠ 0.5kg(机器不正常) - 设置显著性水平:
α = 0.05 - 根据问题选择假设检验的方式:
根据题意已知糖的净重呈正态分布且总体标准差已知,故选择Z检验。 - 计算统计量,并通过统计量获取P值。
from scipy import stats
a = np.array([0.497,0.506,0.518,0.524,0.498,0.511,0.520,0.515,0.512])
#总体的均值和标准差
mean, std = 0.5, 0.015
#计算样本均值
sample_mean = a.mean()
#计算标准误差
se = std/np.sqrt(len(a))
#计算Z统计量
Z = (sample_mean-mean)/se
print('统计量Z:',Z)
#计算P值
p = 2*stats.norm.sf(abs(z))
print('P-Value值:', p)
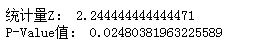
通过结果可知,P值小于0.05,则拒绝原假设,接受备择假设,我们可以认为机器运作不正常。
t检验
t检验与Z检验类似,用来判断样本均值是否与总体均值均有显著性差异。不过t检验是基于t分布的,适用于:
- 总体呈正态分布。
- 总体方差未知。
- 样本数量较少(<30)
不过,随着样本容量的增大(样本数量≥30),t分布逐渐接近于正态分布。此时,t检验也就近似于Z检验。
t统计量计算公式:
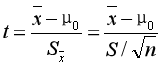
- ¯x:样本均值。
- μ0:待检验的总体均值(假设的总体均值)。
- Sx:样本均值的标准差(标准误差)。
- S:样本的标准差。
- n:样本容量。
例:鸢尾花的平均花瓣长度为3.5cm,这种说法正确吗?
可以根据假设检验的步骤,进行解决。
- 设置原假设与备择假设:
原假设:μ = μ0 = 3.5cm(说法正确)
备择假设:μ ≠ μ0 ≠ 3.5cm(说法不正确) - 设置显著性水平:
α = 0.05 - 根据问题选择假设检验的方式:
鸢尾花数据呈正态分布,但总体标准差未知,故选择t检验。 - 计算统计量,并通过统计量获取P值。
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
data = pd.DataFrame(iris.data, columns=['sepal_length','sepal_width','petal_length','petal_width'])
#计算样本均值、标准差
mean = data['petal_length'].mean()
std = data['petal_length'].std()
print('样本均值:',mean)
print('样本标准差:',std)
#计算t统计量
t = (mean-3.5)/(std/np.sqrt(len(data['petal_length'])))
print('t统计量:', t)
#计算p值
#df:自由度,即变量可以自由取值的个数
p = 2*stats.t.sf(abs(t), df=len(data['petal_length'])-1)
print('P-Value值:', p)

可以看到P值大于0.05,我们没有充分的理由拒绝原假设,则接受原假设,拒绝备择假设。
ps: 我们也可以通过scipy提供的相关方法进行t检验的计算(仅支持双边t检验)
stats.ttest_1samp(data['petal_length'], 3.5)
![]()
可以看到,使用scipy计算的结果,与自行计算的结果相同(忽略小数存储的误差)。
单边检验
有时候,我们关注的不是总体参数是否等于假设参数值,而是总体参数大于或小于假设参数值,这样的检验称为单边假设检验(单边检验)。如,我们关注的是机器改进后,生产能力是否有提高,而不是是否与之前不同。
以均值为例,设总体均值为μ,假设均值为μ0,如果设:
- 原假设:μ ≤ μ0
- 备择假设:μ > μ0
则称这样的检验为右边假设检验(右边检验)。
如果设:
- 原假设:μ ≥ μ0
- 备择假设:μ < μ0
则称这样的检验为左边假设检验(左边检验)。
说明:
- 在单边检验中,原假设为维持现状,备择假设为改变现状。
- 单边检验与双边检验计算统计量的方式是相同的,得出的P值不同(概率值不同)。
右边假设检验
如果把上面鸢尾花的问题改为:
鸢尾花的平均花瓣长度不超过3.5cm吗?
这就是一个右边假设检验的问题,求解过程如下:
- 设置原假设与备择假设:
原假设:μ ≤ μ0 (小于等于3.5cm说法正确)
备择假设:μ > μ0 (小于等于3.5cm说法不正确) - 设置显著性水平:
α = 0.05 - 根据问题选择假设检验的方式:
鸢尾花数据呈正态分布,但总体标准差未知,故选择t检验。 - 计算统计量,并通过统计量获取P值。
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
data = pd.DataFrame(iris.data, columns=['sepal_length','sepal_width','petal_length','petal_width'])
#计算样本均值、标准差
mean = data['petal_length'].mean()
std = data['petal_length'].std()
#计算t统计量
t = (mean-3.5)/(std/np.sqrt(len(data['petal_length'])))
print('t统计量:', t)
#计算p值
#df:自由度,即变量可以自由取值的个数
p = stats.t.sf(t, df=len(data['petal_length'])-1)
print('P-Value值:', p)
![]()
从结论可以看出P值小于0.05,拒绝原假设,则我们可以认为花瓣长度超过3.5cm。
左边假设检验
我们可以把上面的问题再次进行修改:
鸢尾花的平均花瓣长度不小于3.5cm吗?
这就是一个左边假设检验的问题,继续求解:
- 设置原假设与备择假设:
原假设:μ ≥ μ0 (大于等于3.5cm说法正确)
备择假设:μ < μ0 (大于等于3.5cm说法不正确) - 设置显著性水平:
α = 0.05 - 根据问题选择假设检验的方式:
鸢尾花数据呈正态分布,但总体标准差未知,故选择t检验。 - 计算统计量,并通过统计量获取P值。
print('t统计量:', t)
#计算p值
#df:自由度,即变量可以自由取值的个数
p = stats.t.cdf(t, df=len(data['petal_length'])-1)
print('P-Value值:', p)