深度强化学习的芯片布局

摘要

在这项工作中，我们提出了一种基于学习的芯片放置方法，这是芯片设计过程中最复杂和最耗时的阶段之一。 与以前的方法不同，我们的方法能够从过去的经验中学习并随着时间的推移而改进。 特别是，当我们训练更多的芯片块时，我们的方法在为以前看不见的芯片块快速生成优化布局方面变得更好。 为了实现这些结果，我们将放置作为强化学习 (RL) 问题，并训练代理将芯片网表的节点放置到芯片画布上。 为了使我们的 RL 策略能够推广到看不见的块，我们在预测放置质量的监督任务中建立了表示学习的基础。 通过设计一种能够准确预测各种网表及其位置的奖励的神经架构，我们能够生成输入网表的丰富特征嵌入。 然后，我们使用这种架构作为我们的策略和价值网络的编码器，以实现迁移学习。 我们的目标是最小化 PPA（功率、性能和面积），我们表明，在 6 小时内，我们的方法可以在现代加速器网表上生成超人或可比的布局，而现有基线需要人类专家参与循环和 需要几个星期

介绍

计算机系统和硬件的显着进步促成了人工智能的快速发展，但随着摩尔定律和登纳德缩放的终结，世界正在转向专用硬件，以满足人工智能对计算呈指数增长的需求。 然而，今天的芯片设计需要数年时间，这让我们不得不为 2-5 年后的机器学习 (ML) 模型优化它们的推测任务。 大幅缩短芯片设计周期将使硬件能够更好地适应快速发展的人工智能领域。 我们相信，正是人工智能本身将提供缩短芯片设计周期的手段，在硬件和人工智能之间建立一种共生关系，相互促进对方的进步。

在这项工作中，我们提出了一种基于学习的芯片放置方法，这是芯片设计过程中最复杂和最耗时的阶段之一。 目标是将宏（例如 SRAM）和标准单元（逻辑门，例如 NAND、NOR 和 XOR）的网表图放置到芯片画布上，从而优化功率、性能和面积 (PPA)， 同时遵守布局密度和布线拥塞的限制（在第 3.3.6 和 3.3.5 节中描述）。 尽管对这个问题进行了数十年的研究，但人类专家仍然需要对现有的放置工具进行数周的迭代，以产生满足多方面设计标准的解决方案。 问题的复杂性源于网表图的大小（数百万到数十亿个节点）、必须放置这些图的网格的粒度以及计算真实目标指标的高昂成本（数小时，有时甚至超过一天） 用于评估单个设计的行业标准电子设计自动化 (EDA) 工具）。 即使将问题分解为更易于管理的子问题（例如，将节点分组为几千个集群并减少网格的粒度），状态空间仍然比基于学习的方法已显示成功的最近问题大几个数量级 .

为了应对这一挑战，我们将芯片放置作为一个强化学习 (RL) 问题，我们训练一个代理（例如，RL 策略网络）来优化放置。 在每次训练迭代中，芯片块的所有宏都由 RL 代理顺序放置，然后通过强制引导方法放置标准单元（Hanan & Kurtzberg, 1972; Tao Luo & Pan, 2008; Bo Hu & Marek-Sadowska，2005；Obermeier 等人，2005；Spindler 等人，2008；Viswanathan 等人，2007b；a)。 训练由代理的每个筹码位置的快速但近似的奖励信号引导。

据我们所知，所提出的方法是第一个具有泛化能力的布局方法，这意味着它可以利用从放置以前的网表中学到的知识来为新的看不见的网表生成布局。 特别是，我们表明，随着我们的代理接触到更多数量和种类的芯片，它在为新芯片块生成优化布局方面变得更快、更好，使我们更接近芯片设计人员由人工辅助的未来。 具有丰富的芯片放置经验的代理商。

我们相信，我们的方法能够从经验中学习并随着时间的推移进行改进，为芯片设计人员开启了新的可能性。 我们表明，与最先进的基线相比，我们可以在真正的 AI 加速器芯片 (Google TPU) 上实现卓越的 PPA。 此外，我们的方法在 6 小时内生成优于或可与人类专家芯片设计师相媲美的布局，而性能最高的替代方案则需要人类专家参与循环，并且对于现代芯片中的数十个模块中的每一个模块都需要数周时间。 虽然我们主要在 AI 加速器芯片上进行评估，但我们提出的方法广泛适用于任何芯片布局优化。

相关工作

全局布局是芯片设计中的一项长期挑战，需要对日益复杂的电路进行多目标优化。 自 1960 年代以来，已经提出了许多方法，到目前为止分为三大类：1) 基于分区的方法，2) 随机/爬山方法，以及 3) 解析求解器。

从 1960 年代开始，工业和学术实验室采用基于分区的方法来解决全局布局问题，提出 (Breuer, 1977; Kernighan, 1985; Fiduccia & Mattheyses, 1982)，以及基于电阻网络的方法 (Chung-Kuan Cheng & Kuh，1984 年；Ren-Song Tsay 等人，1988 年）。 这些方法的特点是分而治之。 网表和芯片画布被递归划分，直到出现足够小的子问题，此时子网表使用最佳求解器放置到子区域上。 这种方法执行速度非常快，并且它们的分层特性允许它们扩展到任意大的网表。 然而，通过孤立地优化每个子问题，基于分区的方法牺牲了全局解决方案的质量，尤其是路由拥塞。 此外，不良的早期分区可能会导致无法挽救的最终布局。

在 1980 年代，分析方法出现了，但很快被随机/爬山算法取代，特别是模拟退火（Kirkpatrick 等人，1983；Sechen 和 Sangiovanni-Vincentelli，1986；Sarrafzadeh 等人，2003）。 模拟退火 (SA) 因其类似于冶金学而得名，其中金属首先被加热然后逐渐冷却以诱导或退火能量最优的晶体表面。 SA 将随机扰动应用于给定的位置（例如，宏的移位、交换或旋转），然后测量它们对目标函数的影响（例如，第 3.3.1 节中描述的半周长线长）。 如果扰动是一种改进，则应用它； 如果不是，它仍然以某种概率应用，称为温度。 温度被初始化为一个特定的值，然后逐渐退火到一个较低的值。 尽管 SA 生成了高质量的解决方案，但它非常缓慢且难以并行化，因此无法扩展到 1990 年代及以后日益庞大和复杂的电路。

1990 年代至 2000 年代的特点是多级划分方法 (Agnihotri et al., 2005; Roy et al., 2007)，以及分析技术的复兴，例如力导向方法 (Tao Luo & Pan, 2008) ; Bo Hu & Marek-Sadowska, 2005; Obermeier 等人, 2005; Spindler 等人, 2008; Viswanathan 等人, 2007b;a) 和非线性优化器 (Kahng 等人, 2005; Chen 等人。 , 2006)。 二次方法的重新成功部分归功于算法的进步，但也归功于现代电路的大尺寸（10-1 亿节点），这证明了将放置问题近似为放置具有零面积的节点的问题。 然而，尽管二次方法的计算效率很高，但它们通常比非线性方法更不可靠并且产生的解决方案质量更低。

非线性优化使用平滑数学函数来近似成本，例如对数和-exp (William et al., 2001) 和线长的加权平均 (Hsu et al., 2011) 模型，以及高斯 (Chen et al. ., 2008) 和亥姆霍兹模型的密度。 然后使用拉格朗日惩罚或松弛将这些函数组合成单个目标函数。 由于这些模型的复杂性较高，有必要采用分层方法，放置集群而不是单个节点，这种近似会降低放置质量。

过去十年见证了现代分析技术的兴起，包括更先进的二次方法（Kim et al., 2010; 2012b; Kim & Markov, 2012; Brenner et al., 2008; Lin et al., 2013）等等 最近，基于静电的方法，如 ePlace (Lu et al., 2015) 和 RePlAce (Cheng et al., 2019)。 ePlace (Lu et al., 2015) 将网表放置建模为静电系统，提出了一种新的密度惩罚公式，其中网表的每个节点（宏单元或标准单元）类似于一个带正电的粒子，其面积对应于其电子 三重收费。 在这种情况下，节点以与其电荷（面积）成比例的力相互排斥，密度函数和梯度对应于系统的势能。 已经提出了这种基于静电的方法的变体来解决标准单元放置 (Lu et al., 2015) 和混合尺寸放置 (Lu et al., 2015; Lu et al., 2016)。 RePlAce (Cheng et al., 2019) 是最近最先进的混合尺寸放置技术，它通过引入局部密度函数来进一步优化 ePlace 的密度函数，该函数为每个单独的 bin 大小定制惩罚因子。 第 5 节将最先进的 RePlAce 算法的性能与我们的方法进行比较。

最近的工作（Huang 等人，2019 年）提出训练一个模型来预测给定宏布局的设计规则检查 (DRC) 违规数量。 DRC 是确保布局和布线的网表符合流片要求的规则。 为了生成具有较少 DRC 的宏布局，（Huang 等人，2019 年）使用来自该训练模型的预测作为模拟退火中的评估函数。 虽然这项工作代表了一个有趣的方向，但它在不超过 6 个宏的网表上报告结果，远远少于任何现代模块，并且该方法不包括布局和布线步骤期间的任何优化。 由于优化，布局和布线可能会发生巨大变化，实际的DRC会相应变化，使模型预测无效。 此外，虽然遵守 DRC 标准是必要条件，但宏布局的主要目标是优化线长、时序（例如最差负松弛 (WNS) 和总负松弛 (TNS)）、功率和面积，以及 这项工作甚至没有考虑这些指标。

领域适应 Domain Adaption

领域适应是训练策略的问题，可以跨多种经验学习并转移获得的知识以在新的看不见的例子上表现更好。 在芯片布局的背景下，域适应涉及在一组芯片网表中训练一个策略，并将该训练后的策略应用于一个新的看不见的网表。 最近，组合优化的域适应已成为一种趋势（Zhou et al., 2019; Paliwal et al., 2019; Addanki et al., 2019）。 虽然先前工作的重点是使用从先前的优化问题示例中学到的领域知识来加快对新问题的策略训练，但我们提出了一种方法，该方法首次通过利用过去的经验来生成更高质量的结果 经验。 与从头开始训练策略相比，我们新颖的域适应不仅产生了更好的结果，而且还减少了 8 倍的训练时间。

方法

3.1。 问题陈述

在这项工作中，我们针对芯片布局优化问题，其目标是将网表（描述芯片的图形）的节点映射到芯片画布（有界 2D 空间）上，以便最终功率、性能 , 面积 (PPA) 得到优化。 在本节中，我们将概述如何将问题表述为强化学习 (RL) 问题，然后详细描述奖励函数、动作和状态表示、策略架构和策略更新。

3.2 方法总述

我们对放置问题采用深度强化学习方法，其中 RL 代理（策略网络）按顺序放置宏； 一旦放置了所有宏，就可以使用强制导向的方法来生成标准单元的粗略放置，如图 1 所示。RL 问题可以表述为马尔可夫决策过程 (MDP)，由四个关键要素组成：
• 奖励：在某个状态下采取行动的奖励。 （例如，可以跨多种经验学习并转移获得的知识以在新的未见示例上表现更好。
• 状态 ：世界可能状态的集合（例如，在我们的例子中，网表在芯片画布上的每个可能的部分放置）。
• 动作：代理可以采取的一组动作（例如，给定当前要放置的宏，可用动作是离散画布空间（网格单元）中可以放置该宏的所有位置的集合 不违反对密度或阻塞的任何硬性限制）。
• 状态转换：给定一个状态和一个动作，这是下一个状态的概率分布。在我们的例子中，除了最后一个动作，奖励是代理线路长度和拥塞的负加权和，所有动作的奖励都是 0，受第 3.3 节所述的密度约束）。
在我们的设置中，在初始状态 s0，我们有一个空的芯片画布和一个未放置的网表。 最终状态 sT 对应于一个完全放置的网表。 在每一步，都会放置一个宏。 因此，T 等于网表中宏的总数。 在每个时间步 t，代理从状态 (st) 开始，采取行动 (at)，到达新状态 (st+1)，并从环境中接收奖励 (rt)（t < T 时为 0，并且 t = T 的负代理成本）。

我们将 st 定义为表示时间 t 状态的特征的串联，包括网表的图嵌入（包括已放置和未放置的节点）、要放置的当前宏的节点嵌入、有关网表的元数据（第 4 节） ，以及表示将当前节点放置到网格的每个单元格上的可行性的掩码（第 3.3.6 节）。
动作空间是第 t 个宏的所有有效位置，它是 3.3.6 节中描述的密度掩码的函数。 动作 $a_t$ 是 RL 策略网络选择的第 t 个宏的单元位置。

st+1 是下一个状态，它包括一个更新的表示，其中包含有关新放置的宏的信息、更新的密度掩码和要放置的下一个节点的嵌入。
在我们的公式中，每个时间步的 rt 都是 0，除了最后的 rT，它是近似线长和拥塞的加权和，如 3.3 节所述。
通过重复的情节（状态、动作和奖励的序列），策略网络学会采取最大化累积奖励的行动。 考虑到每个位置的累积奖励，我们使用近端策略优化 (PPO) (Schulman et al., 2017) 来更新策略网络的参数。
在本节中，我们定义了奖励 r、状态 s、动作 a、由 θ 参数化的策略网络架构 πθ(a|s)，最后是我们用来训练这些参数的优化方法。

3.3奖励

我们在这项工作中的目标是最小化功耗、性能和面积，但要受到路由拥塞和密度的限制。 我们真正的回报是商业 EDA 工具的输出，包括线长、布线拥塞、密度、功率、时序和面积。 然而，RL 策略需要 100,000 个示例才能有效学习，因此快速评估奖励函数至关重要，理想情况下在几毫秒内运行。 为了有效，这些近似奖励函数也必须与真实奖励正相关。 因此，我们成本的一个组成部分是线长，因为它不仅评估成本低得多，而且与功率和性能（时序）相关。 我们分别为线长和拥塞定义了近似成本函数，如第 3.3.1 节和第 3.3.5 节所述。
为了将多个目标组合成一个单一的奖励函数，我们采用代理线长和拥塞的加权和，其中权重可用于探索两个指标之间的权衡。 虽然我们将拥塞视为软约束（即，较低的拥塞改善了奖励函数），但我们将密度视为硬约束，屏蔽了密度超过目标密度的动作（放置节点的网格单元），如第 1 节中进一步描述的那样 3.3.6。
为了保持每次迭代的运行时间较小，我们在奖励函数的计算中应用了几个近似值：

1. 我们使用 hMETIS (Karypis & Kumar, 1998) 将数百万个标准单元分组到数千个集群中，这是一种基于归一化的分区技术 最小切割目标。 一旦放置了所有宏，我们使用强制导向的方法来放置标准单元簇，如第 3.3.4 节所述。 这样做使我们能够达到近似但快速的 便于策略网络优化的标准小区布局。
2. 我们将网格离散为几千个网格单元，并将宏和标准单元簇的中心放置在网格单元的中心。
3. 在计算线长时，我们做了一个简化的假设，即所有离开标准单元簇的导线都起源于簇的中心。
4. 为了计算路由拥塞成本，我们只考虑前 10% 最拥塞的网格单元的平均拥塞，如 3.3.5 节所述。

线长 根据文献 (Shahookar & Mazumder, 1991)，我们采用半周线长 (HPWL)，这是线长最常用的近似值。 HPWL 定义为网表中所有节点的边界框的半周长。 给定网络（边）i 的 HPWL 如下等式所示：

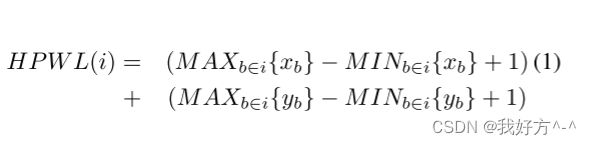
这里 xb 和 yb 显示了网络 i 端点的 x 和 y 坐标。 然后通过取所有半周边界框的归一化总和来计算总 HPWL 成本，如公式 2 所示。q(i) 是一个归一化因子，它通过将线长成本增加为 节点增加，其中 Nnetlist 是网络的数量。

直观地说，给定布局的 HPWL 大致是其 Steiner 树的长度 (Gilbert & Pollak, 1968)，这是布线成本的下限。 线长还具有与其他重要指标相关联的优势，例如功率和时序。 尽管我们没有直接针对这些其他指标进行优化，但我们观察到了功耗和时序方面的高性能（如表 2 所示）。

3.3.2. 网格行和列的选择

考虑到芯片画布的尺寸，有许多选择可以将 2D 画布离散为网格单元。 这个决定会影响优化的难度和质量的最终位置。 我们将最大行数和列数限制为 128。我们将选择最佳行数和列数视为装箱问题，并根据所浪费的空间量对行和列的不同组合进行排名。 在第 5 节中描述的实验中，我们平均使用 30 行和列。
3.3.3. 选择宏顺序 为了选择放置宏的顺序，我们按大小降序对宏进行排序，并使用拓扑排序打破平局。 通过首先放置较大的宏，我们减少了后面的宏没有可行放置的机会。 拓扑排序可以帮助策略网络学会将连接的节点彼此靠近。 另一种可能的方法是学习联合优化宏的顺序及其放置，选择将哪个节点放置在动作空间的下一部分。 然而，这种扩大的行动空间会显着增加问题的复杂性，我们发现这种启发式在实践中是有效的。
3.3.4。 标准单元放置 为了放置标准单元簇，我们使用类似于经典的力导向方法（Shahookar & Mazumder，1991）的方法。 我们将网表表示为一个弹簧系统，根据权重 × 距离公式，向每个节点施加力，导致紧密连接的节点相互吸引。 我们还在重叠节点之间引入排斥力以降低放置密度。 施加所有力后，我们沿力矢量的方向移动节点。 为了减少振荡，我们为每次移动设置了最大距离。

3.3.5。 路由拥塞我们在计算代理拥塞时也遵循惯例（Kim et al., 2012a），使用基于驱动程序位置和网络负载的简单确定性路由。 布线网络为其通过的每个网格单元占用一定数量的可用布线资源（由底层半导体制造技术确定）。 我们分别跟踪每个网格单元中的垂直和水平分配。 为了平滑拥塞估计，我们在垂直和水平方向上运行 5×1 卷积滤波器。 在所有网络都被路由之后，我们取前 10% 的拥塞值的平均值，从 MAPLE 中的 ABA10 指标中汲取灵感（Kim et al., 2012a）。 等式 4 中的拥塞成本是此过程计算的前 10% 的平均拥塞。
3.3.6。 DENSITY 我们将密度视为硬约束，不允许策略网络将宏放置在会导致密度超过目标（最大密度）或导致不可行的宏重叠的位置。 这种方法有两个好处：（1）它减少了策略网络生成的无效布局的数量，（2）它减少了优化问题的搜索空间，使其在计算上更易于处理。 一个可行的标准单元簇放置应满足以下标准：每个网格单元中放置的项目的密度不应超过给定的目标密度阈值（最大密度）。 我们在实验中将此阈值设置为 0.6。 为了满足这个约束，在每个 RL 步骤中，我们计算当前密度掩码，一个二进制 m×n 矩阵，表示我们可以在不违反密度阈值标准的情况下放置当前节点的中心的网格单元。 在从策略网络输出中选择一个动作之前，我们首先取掩码和策略网络输出的点积，然后在可行位置上取 argmax。 这种方法可以防止策略网络生成具有重叠宏或密集标准单元区域的布局。 我们还通过将阻塞区域的密度函数设置为 1 来启用阻塞感知布局（例如时钟带）。
3.3.7。 后处理 为了准备放置以供商业 EDA 工具评估，我们执行了一个贪婪的合法化步骤，以将宏捕捉到最近的合法位置，同时遵守最小间距限制。 然后我们修复宏布局并使用 EDA 工具来放置标准单元并评估布局。

3.4动作表示

出于策略优化的目的，我们将画布转换为 m × n 网格。 因此，对于任何给定的状态，动作空间（或策略网络的输出）是当前宏在 m × n 网格上的位置的概率分布。 动作是这个概率分布的 argmax。

3.5. 状态表示

我们的状态包含有关网表图（邻接矩阵）、其节点特征（宽度、高度、类型等）、边缘特征（连接数）、要放置的当前节点（宏）和元数据的信息 网表和底层技术（例如，路由分配、导线总数、宏和标准单元簇等）。 在下一节中，我们将讨论如何处理这些特征来学习芯片放置问题的有效表示。

域迁移：从经验中学习更好的芯片放置

我们的目标是开发 RL 代理，当他们获得放置芯片的经验时，可以产生更高质量的结果。 我们可以正式定义放置目标函数如下：

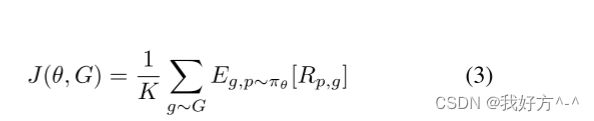
这里 J(θ, G) 是成本函数。 代理由 θ 参数化。 大小为 K 的网表图的数据集用 G 表示，数据集中的每个单独的网表都写为 g。 Rp,g 是从应用于网表 g 的策略网络中抽取的放置 p 的情节奖励。

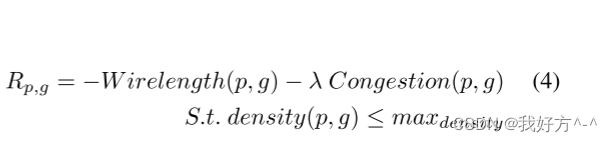
等式 4 显示了我们用于策略网络优化的奖励，它是受密度约束的线路长度和拥塞的负加权平均值。 奖励在第 3.3 节中详细解释。 在我们的实验中，拥塞权重 λ 设置为 0.01，最大密度阈值设置为 0.6。

4.1一种实现迁移学习的监督方法

我们提出了一种新颖的神经架构，使我们能够训练用于芯片放置的域自适应策略。 训练这样一个策略网络是一项具有挑战性的任务，因为包含所有可能芯片的所有可能布局的状态空间是巨大的。 此外，不同的网表和网格大小可以具有非常不同的属性，包括不同数量的节点、宏大小、图形拓扑以及画布宽度和高度。 为了应对这一挑战，我们首先专注于学习状态空间的丰富表示。 我们的直觉是，能够跨芯片传输布局优化的策略网络架构也应该能够在推理时将与新的未见过芯片相关的状态编码为有意义的信号。 因此，我们建议训练一种能够预测新网表奖励的神经网络架构，最终目标是使用该架构作为我们策略网络的编码器层。
为了训练这个有监督的模型，我们需要一个大型的芯片放置数据集及其相应的奖励标签。 因此，我们创建了一个包含 10,000 个芯片布局的数据集，其中输入是与给定布局相关的状态，标签是该布局的奖励（线长和拥塞）。 我们首先选择 5 个不同的加速器网表，然后为每个网表生成 2,000 个布局来构建这个数据集。 为了为每个网表创建不同的布局，我们在各种拥塞权重（范围从 0 到 1）和随机种子下训练了一个普通策略网络，并在策略训练过程中收集了每个布局的快照。 未经训练的策略网络以随机权重开始，生成的位置质量低，但随着策略网络的训练，生成位置的质量提高，使我们能够收集具有不同质量位置的多样化数据集。
为了训练一个可以准确预测线长和拥塞标签并泛化到看不见的数据的监督模型，我们开发了一种新的图神经网络架构，该架构嵌入了有关网表的信息。 图神经网络的作用是将关于大图中节点的类型和连通性的信息提炼成可用于下游任务的低维向量表示。 此类下游任务的一些示例包括节点分类 (Nazi et al., 2019)、设备放置 (Zhou et al., 2019)、链接预测 (Zhang & Chen, 2018) 和设计规则违规 (DRCs) 预测 (Zhiyao Xie 杜克大学，2018）。
我们通过连接节点特征来创建每个节点的向量表示。 节点特征包括节点类型、宽度、高度以及 x 和 y 坐标。 我们还将节点邻接信息作为输入传递给我们的算法。 然后我们重复执行以下更新：1）每个边通过将完全连接的网络应用于中间节点嵌入的聚合表示来更新其表示，以及 2）每个节点通过取相邻边嵌入的平均值来更新其表示。 节点和边更新如公式 5 所示。

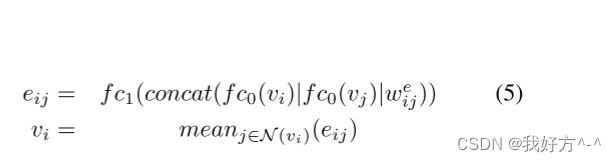
节点嵌入用 vis 表示，1 <= i <= N，其中 N 是宏和标准单元簇的总数。 连接节点 vi 和 vj 的向量化边表示为 eij。 边 (eij) 和节点 (vi) 嵌入都是随机初始化的，并且是 32 维的。 fc0 是一个 32×32，fc1 是一个 65×32 的前馈网络，我们 ijs 是对应于边的可学习的 1x1 权重。 N(vi) 显示 vi 的邻居。 该算法的输出是节点和边嵌入。

我们的监督模型包括：（1）上面描述的图神经网络，它嵌入了关于节点类型和网表邻接矩阵的信息。 (2) 嵌入元数据的全连接前馈网络，包括有关底层半导体技术（水平和垂直路由能力）、网络总数（边）、宏和标准单元簇、画布大小和行数的信息 和网格中的列。 (3) 一个全连接的前馈网络（预测层），其输入是网表图和元数据嵌入的串联，其输出是奖励预测。 网表图嵌入是 (5) 通过在边缘嵌入上应用归约均值函数创建的。 监督模型通过回归进行训练，以最小化线长和拥塞的均方损失的加权和。
这项有监督的任务使我们能够找到跨网表泛化奖励预测所需的特征和架构。 为了将此架构整合到我们的策略网络中，我们移除了预测层，然后将其用作策略网络的编码器组件，如图 2 所示。为了处理对应于不同行和列选择的不同网格大小，我们设置了网格 大小为 128 × 128，并为小于 128 行和列的网格大小屏蔽未使用的 L 形部分。
为了在推理时放置一个新的测试网表，我们加载了策略网络的预训练权重并将其应用于新的网表。 我们将没有微调的预训练策略网络生成的展示位置称为零样本展示位置。 这样的布局可以在不到一秒的时间内生成，因为它只需要预先训练的策略网络的一个推理步骤。 我们可以通过微调策略网络来进一步优化放置质量。 这样做使我们可以灵活地使用预训练的权重（已经学习了输入状态的丰富表示）或进一步微调这些权重以优化特定芯片网表的属性。

4.2. 政策网络架构

图 2 描绘了政策网络（由等式 3 中的 πθ 建模）和我们为芯片放置开发的价值网络架构的概述。 这些网络的输入是网表图（图邻接矩阵和节点特征）、要放置的当前节点的 id 以及网表和半导体技术的元数据。 如前所述，网表图通过我们提出的图神经网络架构传递。 该图神经网络生成 (1) 部分放置的图和 (2) 当前节点的嵌入。 我们使用一个简单的前馈网络来嵌入 (3) 元数据。 然后将这三个嵌入向量连接起来形成状态嵌入，然后将其传递给前馈神经网络。 然后将前馈网络的输出馈送到策略网络（由 5 个反卷积层 1 和批量归一化层组成）以生成动作的概率分布，并传递给价值网络（由前馈网络组成）以预测 输入状态。

4.3. 策略网络更新：

训练参数 θ 在等式 3 中，目标是训练一个策略网络 πθ，在策略网络的布局分布上最大化奖励 (Rp,g) 的期望值 (E)。 为了优化策略网络的参数，我们使用具有裁剪目标的近端策略优化 (PPO) (Schulman et al., 2017)：

其中 E^t 表示时间步 t 的期望值，rt 是新策略和旧策略的比率，A^t 是时间步 t 的估计优势。

结果【回答三个问题】

在本节中，我们评估我们的方法并回答以下问题：

1. 我们的方法是否能够实现域迁移和从经验中学习？
2. 使用预训练策略对结果质量有何影响？
3. 生成的展示位置的质量与最先进的基线相比如何？
   我们还检查了生成的展示位置的视觉外观，并就我们的政策网络做出这些决定的原因提供了一些见解。

5.1。 迁移学习结果

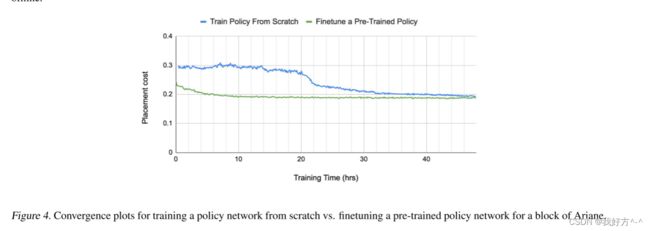
图 3 将使用预训练策略生成的展示位置质量与从头训练策略网络生成的展示位置质量进行了比较。 零样本意味着我们将预训练的策略网络应用到新的网表中，无需微调，在不到一秒的时间内产生布局。 我们还展示了我们在 2 和 12 小时内针对特定设计的细节对预训练策略网络进行微调的结果。 从头开始训练的策略网络需要更长的时间才能收敛，即使在 24 小时后，结果也比经过微调的策略网络在 12 小时后达到的效果更差，这表明学习到的权重和接触许多不同的设计正在帮助我们实现更高的 在更短的时间内为新设计提供高质量的展示位置。 图 4 显示了从头开始训练与 Ariane RISC-V CPU 的预训练策略网络训练的收敛图。 预训练的策略网络在微调过程开始时以较低的放置成本开始。 此外，预训练的策略网络收敛到较低的放置成本，并且比从头开始训练的策略网络快 30 多个小时。

5.2. 从更大的数据集中学习

随着我们在更多的芯片块上进行训练，我们能够加快训练过程并更快地产生更高质量的结果。 图 5（左）显示了更大的训练集对性能的影响。 训练数据集是从内部 TPU 块创建的。 训练数据由各种块组成，包括内存子系统、计算单元和控制逻辑。 随着我们将训练集从 2 个块增加到 5 个块，最后增加到 20 个块，策略网络在零样本和相同小时数的微调后生成更好的布局。 图 5（右）显示了测试数据的放置成本，因为策略网络正在（预）训练。 我们可以看到，对于小的训练数据集，策略网络快速过拟合到训练数据并且在测试数据上的性能下降，而策略网络在最大数据集上过拟合以及在更大数据集上预训练的策略网络需要更长的时间 dataset 在测试数据上产生更好的结果。 该图表明，当我们将策略网络暴露给更多种类的不同块时，虽然策略网络可能需要更长的时间进行预训练，但策略网络变得不太容易过度拟合，并且更好地为新的看不见的块找到优化的位置 块。

5.3. Visualization Insights

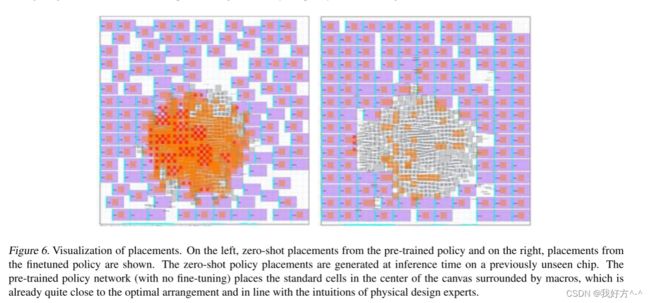
图 6 显示了 Ariane RISCV CPU 的布局结果。 左侧显示了来自零样本策略网络的放置，右侧显示了来自微调策略网络的放置。 零样本放置是在推理时在以前看不见的芯片上生成的。 零样本策略网络将标准单元放置在被宏包围的画布中心，这已经非常接近最优排列。 微调后，宏的放置变得更加规则化，中心的标准单元区域变得不那么拥挤。 图 7 显示了可视化的放置：左侧显示了手动放置的结果，右侧显示了我们方法的结果。 白色区域显示宏放置，绿色区域显示标准单元放置。 我们的方法在标准单元周围创建了环形的宏放置，从而减少了总线长。

5.4. 与基线方法比较

在本节中，我们将我们的方法与 3 种基线方法进行比较：模拟退火、RePlAce 和人类专家基线。 对于我们的方法，我们使用在最大数据集（20 个 TPU 块）上预训练的策略，然后在块 1 到 5 表示的 5 个未见过的目标块上对其进行微调。我们的数据集由各种块组成，包括内存子系统、计算单元 和控制逻辑。 由于机密性，我们无法透露这些区块的详细信息，但为了了解规模，每个区块最多包含数百个宏和数百万个标准单元。
与模拟退火的比较：
众所周知，模拟退火 (SA) 是一种强大但缓慢的优化方法。 然而，与 RL 一样，模拟退火能够优化任意不可微的成本函数。 为了显示 RL 的相对样本效率，我们进行了实验，将其替换为基于模拟退火的优化器。 在这些实验中，我们使用与之前相同的输入和成本函数，但在每一集中，模拟退火优化器放置所有宏，然后是 FD 步骤放置标准单元簇。 根据 SA 更新规则，使用指数衰减退火计划（Kirkpatrick 等人，1983）接受每个宏布局。 SA 需要 18 小时才能收敛，而我们的方法不超过 6 小时。 为了公平比较，我们运行了多个 SA 实验，扫描不同的超参数，包括最小和最大温度、种子和最大 SA 集，这样 SA 和 RL 在模拟中花费相同数量的 CPU 小时并搜索相似数量 的州。 表 1 中报告了以最低成本进行的实验结果。如表所示，即使有额外的时间，与我们的方法相比，SA 仍难以生产高质量的贴装，并且生产的贴装线长度增加 14.4%，增加 24.1% 平均拥堵。

与RePlAce的比较（Cheng等人2019年）和手动基线：
表2比较了我们的结果和最先进的方法RePlAce（Cheng等人2019年）和手动基线。手动基线是由生产芯片设计团队生成的，并涉及多次布局优化迭代，在来自商业EDA工具的反馈指导下，经过数周的时间。对于RePlAce，我们具有相同的优化目标，即在芯片设计中优化全局布局，但是我们使用不同的目标函数。因此，我们不是比较不同成本函数的结果，而是将商业EDA工具的输出视为基础真理。为了执行此比较，我们修复了由我们的方法和RePlAce生成的宏放置，并允许商业EDA工具使用该工具的默认设置进一步优化标准单元放置。然后我们报告总有线长度、时间（最差（WNS）和总（TNS）负松弛）、面积和功率指标。如表2所示，我们的方法在生成满足设计要求的放置方面优于RePLAce。给定由底层半导体技术施加的约束，如果WNS显著高于100 ps或者如果水平或垂直拥塞超过1%，则这些块的放置将不能满足设计流程的后期阶段中的时序约束，使得一些RePlAce放置（块1，2，3）不可用。这些结果表明，我们的拥塞感知方法能够有效地生成满足设计标准的高质量布局。

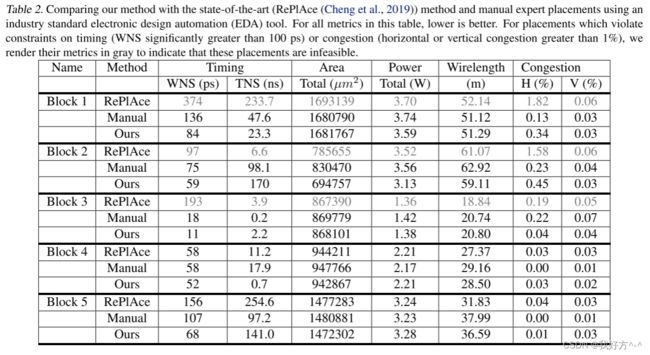
RePlAce 比我们的方法更快，因为它在 1 到 3.5 小时内收敛，而我们的结果是在 3 到 6 小时内实现的。 然而，我们的方法的一些基本优势是 1) 我们的方法可以很容易地优化各种不可微分的成本函数，而不需要制定这些成本函数的封闭形式或可微等价物。 例如，虽然将线长建模为凸函数很简单，但对于布线拥塞或时序却不是这样。 2）我们的方法能够随着时间的推移而改进，因为策略暴露于更多的芯片块，3）我们的方法能够遵守各种设计约束，例如不同形状的阻塞。 表 2 还显示了人类专家芯片设计人员生成的结果。 我们的方法和人工专家都始终如一地生成可行的布局，这意味着它们符合时序和拥塞设计标准。 我们还在 WNS、面积、功率和线长方面优于或匹配手动放置。 此外，我们基于端到端学习的方法只需不到 6 个小时，而手动基线涉及一个缓慢的迭代优化过程，需要专家参与，并且可能需要数周时间。

5.5. 讨论

进一步优化我们方法的机会：有多种机会可以进一步提高我们方法的质量。 例如，标准单元格划分、行列选择以及选择宏放置顺序的过程都可以进一步优化。 此外，我们还将受益于更优化的标准单元放置方法。 目前，由于其运行速度快，我们使用强制导向的方法来放置标准单元。 然而，我们相信更先进的标准单元放置技术，如 RePlAce (Cheng et al., 2019) 和 DREAMPlace (Lin et al., 2019) 可以产生更准确的标准单元放置来指导策略网络训练。 这很有帮助，因为如果策略网络对其宏布局如何影响标准单元布局和最终指标有更清晰的信号，它可以学会做出更优化的宏布局决策。
对更广泛问题的影响：这项工作只是优化领域自适应策略的一个示例，可以扩展到芯片设计过程的其他阶段，例如架构和逻辑设计、综合和设计验证，目标是 的训练 ML 模型随着遇到更多问题实例而改进。 基于学习的方法还可以在构成芯片设计过程的级联任务中实现进一步的设计空间探索和协同优化。

结论

在这项工作中，我们针对芯片放置的复杂而有影响力的问题。我们提出了一种基于RL的方法，该方法可实现转移学习，这意味着RL代理在芯片放置方面变得更快，更好，因为它获得了更多芯片网表的经验。我们证明，我们的方法优于最先进的基准，并且可以生成与现代加速器上的人类专家更好或可比的位置。我们的方法是端到端的，并在不到6小时的时间内生成放置位置，而最强的基线需要人工专家在循环中并且需要数周的时间。

关注

1. google强化学习做芯片布局 【可能是数字芯片，很多约束可以忽略？-> 】使用强制导向的方法来放置标准单元
2. 目前最先进的解析法 RePlAce (Cheng et al., 2019)最近最先进的混合尺寸放置技术，它通过引入局部密度函数来进一步优化 ePlace 的密度函数，该函数为每个单独的 bin 大小定制惩罚因子
3. 合优化的域适应已成为一种趋势（Zhou et al., 2019; Paliwal et al., 2019; Addanki et al., 2019） 【领域适应的概念】
4. 路由拥塞我们在计算代理拥塞时也遵循惯例（Kim et al., 2012a）