动手学深度学习笔记1-线性回归从0到1实现

from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd,nd
import random

#生成数据集，训练数据集样本数1000，输入个数特征数2
num_inputs = 2
num_examples = 1000
#真实权重
true_w = [2,-3.4]
#偏差
true_b = 4.2
features = nd.random.normal(scale=1,shape=(num_examples,num_inputs))
labels = true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
labels += nd.random.normal(scale=0.01,shape=labels.shape)

features[0],labels[0]

(
 [1.1630785 0.4838046]
 ,
 
 [4.879625]
 )

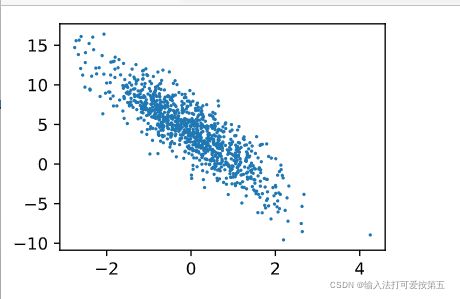
#生成第二个特征和标签的散点图 ，直观的观察两者的线性关系
def use_svg_display():
    #用矢量图显示
    display.set_matplotlib_formats('svg')
    
def set_figsize(figsize=(3.5,2.5)):
    use_svg_display()
    #设置图的尺寸
    plt.rcParams['figure.figsize'] = figsize

set_figsize()
plt.scatter(features[:,1].asnumpy(),labels.asnumpy(),1);#加分号只显示图

​

​

#读取数据集
#定义一个函数，返回batch_size(批量大小)个随机样本的特征和标签
def data_iter(batch_size,features,labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices) #随机读取样本
    for i in range(0,num_examples,batch_size):
        j = nd.array(indices[i:min(i+batch_size,num_examples)])
        yield features.take(j),labels.take(j)

batch_size = 10
for X,y in data_iter(batch_size,features,labels):
    print(X,y)
    break

[[-1.4992921   1.2127866 ]
 [-0.956808   -0.6704501 ]
 [ 0.347244    0.6383554 ]
 [ 0.5195598   0.9168663 ]
 [-1.0837995  -0.47645685]
 [ 0.7099881   0.03483092]
 [-1.2217871   1.5179309 ]
 [ 1.1756743   0.5103031 ]
 [ 1.1317449  -1.090209  ]
 [-0.04268014 -1.0699745 ]]
 
[-2.9186268  4.5762944  2.7228804  2.0938976  3.6574364  5.4816027
 -3.4120479  4.815456  10.172919   7.7523017]

#初始化模型参数
#权重初始化为均值为0，标准差为0.01的正态随机数，偏差初始化为0
w = nd.random.normal(scale=0.01,shape=(num_inputs,1))
b = nd.zeros(shape=(1,))
#创建梯度
w.attach_grad()
b.attach_grad()

#定义模型
#dot函数做矩阵乘法
def linreg(X,w,b):
    return nd.dot(X,w)+b

#定义损失函数
def squared_loss(y_hat,y):
    return (y_hat-y.reshape(y_hat.shape))**2/2

#定义优化算法
#小批量随机梯度下降法，通过不断迭代模型函数来优化损失函数
def sgd(params,lr,batch_size):
    for param in params:
        param[:] = param - lr*param.grad/batch_size

#训练模型
#迭代周期和学习率都是超参数，自己设置
#训练：多次迭代模型参数，读取的batch_size，调用反向函数backward计算小批量随机梯度，调用优化算法sgd迭代模型参数
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):#训练模型需要多少个迭代周期
    #每一个迭代周期，使用训练样本一次
    for X,y in data_iter(batch_size,features,labels):
        with autograd.record():
            l = loss(net(X,w,b),y)  #l是有关小批量X和y的损失
        l.backward() #小批量损失对模型参数求梯度
        sgd([w,b],lr,batch_size)
    train_l = loss(net(features,w,b),labels)
    print('epoch %d,loss %f'%(epoch+1,train_l.mean().asnumpy()))
    

epoch 1,loss 0.035184
epoch 2,loss 0.000125
epoch 3,loss 0.000048

true_w,w

([2, -3.4],
 
 [[ 1.9996485]
  [-3.3998017]]
 )

true_b,b

(4.2,
 
 [4.2001934]
 )