Towards Ultra-Resolution Neural Style Transfer via Thumbnail Instance Normalization

碎碎念：毕设打算做风格迁移的，然而没有接触过这方面，记录一下qwq

Abstract

基于现有的风格迁移框架处理高分辨率有以下缺点：

• 内存成本
• 笔触过小

针对上述两点问题，本文提出Ultra-Resolution Style Transfer（URST）框架。
针对内存问题，URST提出：

1. 将图像划分为patch
2. 提出Thumbnail Instance Normalization（TIN）执行基于patch的风格迁移。TIN可提取缩略图特征的归一化统计信息，并应用于patch，保证了不同patch间的风格一致性

基于本文实验，总结URST有以下优点：

• 将输入图像切割为patch，同时采用TIN技术，实现任意分辨率的风格迁移
• 得益于笔触感知损失stroke perceptual loss在扩大笔触URST在超高分辨率上优于现有的SOTA方法
• URST易于嵌入现有的风格迁移算法方法中，无需训练即可提高性能

Introduction

随着深度学习的发展，风格迁移已取得了显著的成功。然而这些工作极少涉及到高分辨率的风格迁移。在自然场景中，超高分辨率图像常出现在大型海报、摄影作品和超高清视频（例如8K）中。在设计超高分辨率图像时，主要有两个需要攻克的问题：

1. 超高分辨率图像处理时的内存成本可能超过GPU内存
2. 在超高分辨率的结果中，较小的笔触尺寸可能会导致不令人满意的纹理密度

针对内存问题，现有方法主要采用轻量级网络架构（Jing et al. 2020）、模型修剪（An et al. 2020）、知识蒸馏（Wang et al. 2020）来降低内存成本。然而现有的方法大多治标不治本。

针对笔触较小的问题，现如今广泛的使用方法是增大笔触尺寸，现有方法大致分为两类：使用大型风格图像进行训练或推理（Jing et al. 2019; Li et al. 2017b; Zhang and Dana 2018），扩大风格迁移网络的感受野。然而这些方法大多需要额外的推理时间和内存，不适合超高分辨率的风格迁移。

本文提出针对超高分辨率的风格迁移框架（URST），步骤简述如下：

1. 采用patch而非完整的图像作为输入，使得在有限的内存资源下处理任意高分辨率图像成为可能
2. 用TIN代替 original instance normalization （IN），以确保不同patch间的风格一致性
3. 提出笔触感知损失作为神经风格迁移的辅助损失，激励风格迁移网络保持大笔触

Related Work

Neural Style Transfer

受卷积神经网络的启发，Gatys, Ecker, and Bethge 2016首次提出基于CNN的风格迁移算法。为加速神经风格迁移，Johnson, Alahi, and Fei-Fei 2016 和Ulyanov et al. 2016采用训练前馈网络以学习特定的艺术风格。近年来，为提高风格迁移的效率，研究人员提出多种风格迁移（Chen et al. 2017; Dumoulin, Shlens, and Kudlur 2017; Li et al. 2017a; Zhang and Dana 2018）和任意风格迁移（Guetal.2018;HuangandBelongie2017;Dengetal.2020;Luetal.2019;Shengetal.2018;Yaoetal.2019）。目前神经风格迁移已取得很大的进展，但由于巨大的内存成本和较小的笔触尺寸，超高分辨率的风格迁移仍具有挑战性。

High-ResolutionNeuralStyleTransfer

限制高分辨率风格迁移的主要因素即是GPU内存。Anetal.2020提出ArtNet，即从GoogLeNet修剪出的用于神经风格迁移的轻量级网络；Jingetal.2020开发了一种基于MobileNet的轻量级网络，与原有的VGG编码器相比，降低了计算复杂性；Wangetal.2020提出了基于蒸馏的方法，即使用预先训练的VGG19作为老师，小型Encoder作为学生，虽然减少了内存消耗，但在处理超高分辨率图像时仍会耗尽GPU内存。

Stroke Size Control in Neural Style Transfer

笔触尺寸是一个重要的感知因素，与风格迁移结果的质量高度相关。通常，带有大笔触的风格化结果往往比小笔触的风格化结果具有更好的外观。Gatysetal.2017首次提出笔触尺寸与损失网络的感受野相关，此团队提出了由粗到细的方法，用大笔触生成风格化的结果。Wangetal.2017提出分层网络来扩大笔触的大小，并用增加尺度的多次损失对其进行训练。Jingetal.2018提出了具有多个笔触分支的特定风格网络MSG-Net，通过缩放风格图像来控制笔触大小。然而这些笔触尺寸控制方法主要针对普通图像分辨率（例如1000*1000像素）下的风格迁移而设计的，难以应用于高分辨率图像。

Proposed Method

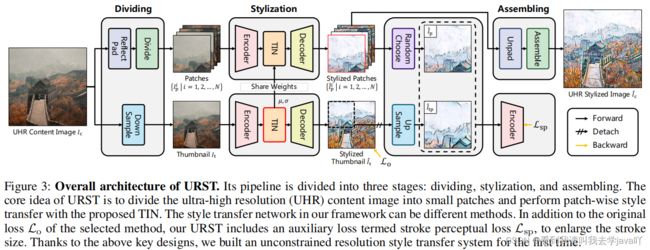
Overall Architecture

URST由三个关键设计模块组成：

• 基于patch的风格迁移，将高成本的风格迁移任务划分为多个低成本的基于patch的风格迁移
• TIN可提取缩略图特征的归一化统计信息，并应用于patch，保证了不同patch间的风格一致性
• 定义笔触感知损失（stroke perceptual loss），激励风格迁移网络保持较大的笔触尺寸

URST步骤简述如下：
以超高分辨率的内容图像$I_c$作为输入，URST可分为三个阶段：划分 dividing、风格化stylization、合成assembling。

1. 在划分阶段，首先为内容图像$I_c$生成一个缩略图$I_t$（下采样），然后将$I_c$划分为patch，即$\{I_p^i|i=1,2,\dots \dots ,N\}$
2. 在风格化阶段，$I_t$首先送入风格迁移网络中手机归一化统计数据，然后利用这些归一化统计数据对patch进行风格化处理，得到风格化的patch，即$\{I_p^i|i=1,2,\dots \dots ,N\}$。注意，此处的风格迁移网络并不是特定的，现有的基于IN的方法都可作为风格迁移网络
3. 在合成阶段，将所有风格化的patch合成一个超高分辨率的风格化图像$I_c$

由于风格化阶段使用的风格迁移网络不同，因而损失函数不同。为方便，本文统一将损失定义为原损失${\mathcal{L}}_o$。
在训练过程中，首先在风格化的缩略图上计算原损失${\mathcal{L}}_o$。此外，URST还引入了辅助损失，即笔触感知损失stroke perceptual loss，以提高超高分辨率风格迁移的质量。其核心思想是针对风格化patch，即$I_p$，和上采样的patch，即$I_{tp}$（来源于风格化缩略图$I_t$），之间的感知差异的惩罚。因此，$I_{tp}$的梯度流是分离的。

Patch-wise Style Transfer

为处理超高分辨率图像，本文提出基于patch的风格迁移。针对给定的超高分辨率的内容图像$I_c$，本文使用一个步长为$S$的$K\ast K$的像素滑动窗口，将$I_c$划分为多个重叠的patch，即$\{I_p^i|i=1,2,\dots \dots ,N\}$。考虑到GPU的内存资源有限，这些patch将分批送入网络中。经过风格化循环，可得到风格化patch，即$\{I_p^i|i=1,2,\dots \dots ,N\}$。最后，删去重叠区域合成完整的图像$I_c$。
与现有的方法相比，基于patch的风格迁移可以灵活处理任意高分辨率图像，也可嵌入现有的风格迁移方法中，例如AdaIN、WCT和LinearWCT。
然而由于每个patch计算的单个归一化统计数据，风格化后的patch其风格显然是不一致的。因此本文提出缩略图实例归一化TIN解决此问题。

Thumbnail Instance Normalization

IN是神经风格迁移中使用广泛的归一化。给定输入张量$x\in {\mathbb{R}}^{N\times C\times H\times W}$，IN计算如下：
$IN(x)=\gamma \left(\frac{x-\mu (x)}{\sigma (x)}\right)+\beta$
其中，$\mu (x),\sigma (x)\in {\mathbb{R}}^{N\times C}$是channel-wise统计，$\gamma ,\beta \in {\mathbb{R}}^C$是可训练仿射参数。
然而，由于基于IN的网络生成的风格化patch在风格上是不一致的，IN并不适合基于patch的风格迁移。Figure 4可说明该问题，即风格不一致的根本原因在于每个patch计算出的单个归一化统计量不同。

基于上述分析，本文提出基于IN的简单变体，即缩略图实例归一化TIN。针对给定的patch $x\in {\mathbb{R}}^{N\times C\times H\times W}$和缩略图$t\in {\mathbb{R}}^{N\times C\times H_t\times W_t}$，TIN计算如下：
$TIN(x,t)=\gamma \left(\frac{x-\mu (t)}{\sigma (t)}\right)+\beta$
其中，$\mu (t),\sigma (t)\in {\mathbb{R}}^{N\times C}$是输入缩略图$t$的channel-wise的均值和标准偏差。
通过此方式，TIN可确保不同的patch其风格一致性。
同样，IW是基于二阶统计量（即协方差矩阵）的标准化方法，被广泛用于神经风格迁移方法中。本文基于IW也提出了TIW，将在补充材料对此进行说明。

Stroke Perceptual Loss

基于所提出的TIN，本文提出扩大笔触尺寸的辅助损失，称为笔触感知损失stroke perceptual loss：
${\mathcal{L}}_{sp}(I_p,I_{tp})=\Vert {\mathcal{F}}_l(I_p)-{\mathcal{F}}_l(I_{tp}){\Vert }^2$
其中，${\mathcal{F}}_l$是VGG网络中该层的输出特征图；$I_p$是小笔触的风格化patch，$I_{tp}$是风格化patch，采用大笔触，裁剪并上采样于风格化的缩略图$I_t$。
由于TIN，输入对$(I_p,I_{tp})$有相同的内容和风格，但是笔触尺寸不同。因此，${\mathcal{L}}_{sp}$主要可以测量笔触感知差异，即优化此损失可激励风格迁移网络生成与目标$I_{tp}$等大的笔触。

Total Loss

总损失函数表现如下：
$\mathcal{L}={\mathcal{L}}_o+\lambda {\mathcal{L}}_{sp}$
其中，$\lambda$是平衡${\mathcal{L}}_o$和${\mathcal{L}}_{sp}$的权重。在本文实验中，$\lambda$默认为$1.0$。