python 用模拟退火算法实现TSP旅行商问题
python 用模拟退火算法实现TSP旅行商问题
计算智能课程作业,使用python实现模拟退火算法实现TSP旅行商问题
问题简介:
给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。它是组合优化中的一个NP困难问题。
代码如下:
#!/usr/bin/python
#_*_ coding:utf-8 _*_
import math
import random
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys
from numpy.matlib import rand
from matplotlib.mlab import dist
from matplotlib.artist import getp
import copy
'''
记录错误,数组直接复制是复制地址
例如, current = route
想要得到一个新的有同样内容的数组,应该用: current = copy.copy(route)
'''
#初始三十个城市坐标
city_x = [1,3,6,12,19,22,23,20,21,22.5,40,44,42,36,39,58,62,88,90,83,71,67,64,52,84,87,71,71,58,80]
city_y = [99,50,64,40,41,42,37,54,60,60.5,26,20,35,83,95,33,30.5,6,38,44,42,57,59,62,65,74,70,77,68,66]
#城市数量
n = 30
distance = [[0 for col in range(n)] for raw in range(n)]
#初始温度 结束温度
T0 = 30
Tend = 1e-8
#循环控制常数
L = 10
#温度衰减系数
a = 0.98
#构建初始参考距离矩阵
def getdistance():
for i in range(n):
for j in range(n):
x = pow(city_x[i] - city_x[j], 2)
y = pow(city_y[i] - city_y[j], 2)
distance[i][j] = pow(x + y, 0.5)
for i in range(n):
for j in range(n):
if distance[i][j] == 0:
distance[i][j] = sys.maxsize
#计算总距离
def cacl_best(rou):
sumdis = 0.0
for i in range(n-1):
sumdis += distance[rou[i]][rou[i+1]]
sumdis += distance[rou[n-1]][rou[0]]
return sumdis
#得到新解
def getnewroute(route, time):
#如果是偶数次,二变换法
current = copy.copy(route)
if time % 2 == 0:
u = random.randint(0, n-1)
v = random.randint(0, n-1)
temp = current[u]
current[u] = current[v]
current[v] = temp
#如果是奇数次,三变换法
else:
temp2 = random.sample(range(0, n), 3)
temp2.sort()
u = temp2[0]
v = temp2[1]
w = temp2[2]
w1 = w + 1
temp3 = [0 for col in range(v - u + 1)]
j =0
for i in range(u, v + 1):
temp3[j] = current[i]
j += 1
for i2 in range(v + 1, w + 1):
current[i2 - (v-u+1)] = current[i2]
w = w - (v-u+1)
j = 0
for i3 in range(w+1, w1):
current[i3] = temp3[j]
j += 1
return current
def draw(best):
result_x = [0 for col in range(n+1)]
result_y = [0 for col in range(n+1)]
for i in range(n):
result_x[i] = city_x[best[i]]
result_y[i] = city_y[best[i]]
result_x[n] = result_x[0]
result_y[n] = result_y[0]
print(result_x)
print(result_y)
plt.xlim(0, 100) # 限定横轴的范围
plt.ylim(0, 100) # 限定纵轴的范围
plt.plot(result_x, result_y, marker='>', mec='r', mfc='w',label=u'Route')
plt.legend() # 让图例生效
plt.margins(0)
plt.subplots_adjust(bottom=0.15)
plt.xlabel(u"x") #X轴标签
plt.ylabel(u"y") #Y轴标签
plt.title("TSP Solution") #标题
plt.show()
plt.close(0)
def solve():
#得到距离矩阵
getdistance()
#得到初始解以及初始距离
route = random.sample(range(0, n), n)
total_dis = cacl_best(route)
print("初始路线:", route)
print("初始距离:", total_dis)
#新解
newroute = []
new_total_dis = 0.0
best = route
best_total_dis = total_dis
t = T0
while True:
if t <= Tend:
break
#令温度为初始温度
for rt2 in range(L):
newroute = getnewroute(route, rt2)
new_total_dis = cacl_best(newroute)
delt = new_total_dis - total_dis
if delt <= 0:
route = newroute
total_dis = new_total_dis
if best_total_dis > new_total_dis:
best = newroute
best_total_dis = new_total_dis
elif delt > 0:
p = math.exp(-delt / t)
ranp = random.uniform(0, 1)
if ranp < p:
route = newroute
total_dis = new_total_dis
t = t * a
print("现在温度为:", t)
print("最佳路线:", best)
print("最佳距离:", best_total_dis)
draw(best)
if __name__=="__main__":
solve()
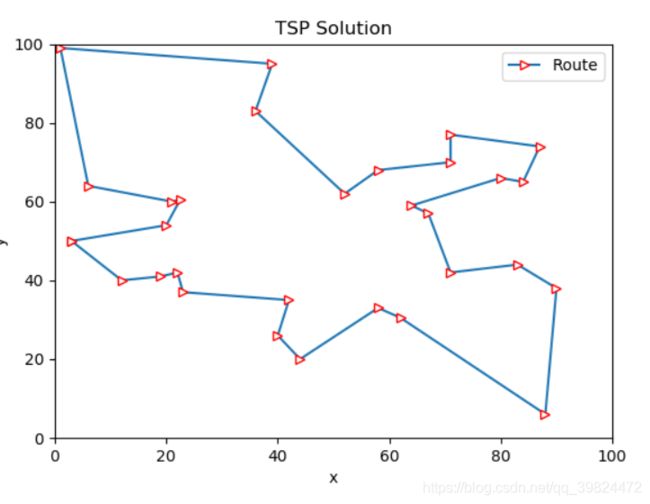
实现效果