EfficientNet解读:神经网络的复合缩放方法(基于tf-Kersa复现代码)
论文:https://arxiv.org/pdf/1905.11946.pdf
代码:https://github.com/qubvel/efficientnet
1、介绍
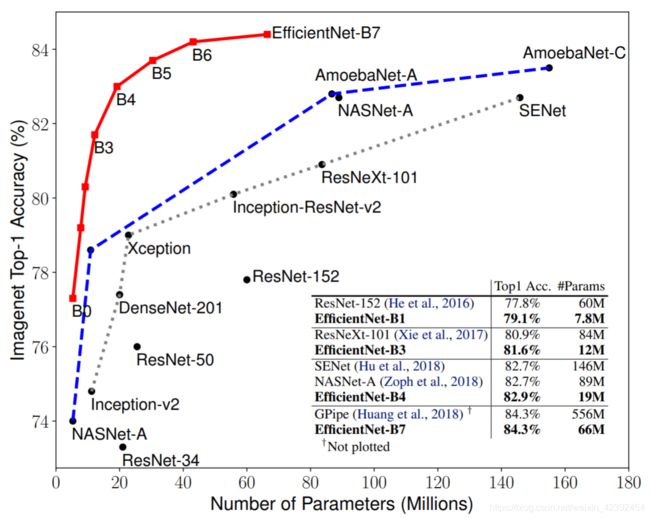
EfficientNet这篇论文在发布之初就引起了广泛关注,原因是因为它展示出的结果将现有的网络全部秒杀了,并且在准确率高出一截的情况下,参数量还少,在ImageNet上屠榜。
看到这让人叹为观止的结果,很多人会认为这篇论文应该是提出了全新的结构,才能做到又快又好。其实并不是这样,作者独辟蹊径,从一个之前完全没有人注意的角度:量化三个维度间的关系,网络的宽度,深度和分辨率。
在之前的工作中,通常只是放大三个维度-深度,宽度,和图像尺寸中的一个维度。尽管可以任意地增大两个或三个维度,但任意的增大需要枯燥的手工调参并且还经常产生次好的准确率和效率。
这篇文章中,作者重新思考下CNN放大的过程。尤其是研究了这个核心问题:是否有一个原则性的方法来增大ConvNets能够达到更好的准确率和效率呢?
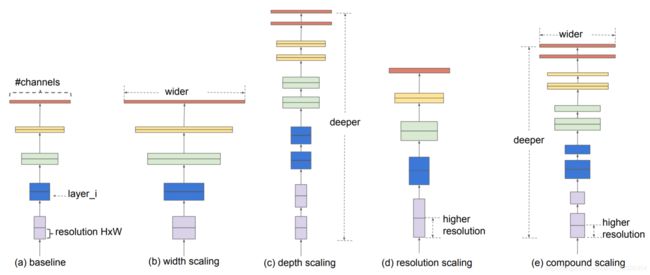
如上图所示,如果我们有一个baseline模型,例如,如果我们想要使用 2 N 2^N 2N倍的更多计算资源,那么我们可以通过 α N \alpha^N αN来增加网络的深度,通过 β N \beta^N βN增加网络的宽度,通过 γ N \gamma^N γN来增加图片的分辨率。(b)-(d)中都是任意增大其中一个系数,(e)则是作者提出的复合缩放方法。
2、问题公式化
定义:
一个ConvNet的第i层定义为: Y i = F i ( X i ) Y_i=F_i(X_i) Yi=Fi(Xi), Y i Y_i Yi是输出的tensor, X i X_i Xi是输入的tensor, F i F_i Fi是卷积层,输入tensor的shape为 < H i , W i , C i >
因此可以将ConvNet统一定义为:
N = ⨀ i = 1... s F i L i ( X < H i , W i , C i > ) N = \bigodot_{i=1...s}F^{L_i}_{i}(X
其中下标i(从1到s)表示的是stage的序号, F i L i F_{i}^{L_i} FiLi代表第i个stage,它由 F i F_i Fi层被重复 L i L_i Li次构成。
与通常的ConvNet设计不同,通常的ConvNet设计主要关注寻找最好的层结构 F i F_i Fi,但本文的作者却反其道而行之。通过常数比例一致地缩放网络宽度、深度和分辨率,而不是对某一个系数进行单独缩放。使得在内存的占用和参数量小于目标阈值的前提下,达到最高的准确率。
用公式表示则为:
其中 w , d , r w,d,r w,d,r分别是网络的宽度,深度和分辨率的系数。其他参数同上。
3、EfficientNet
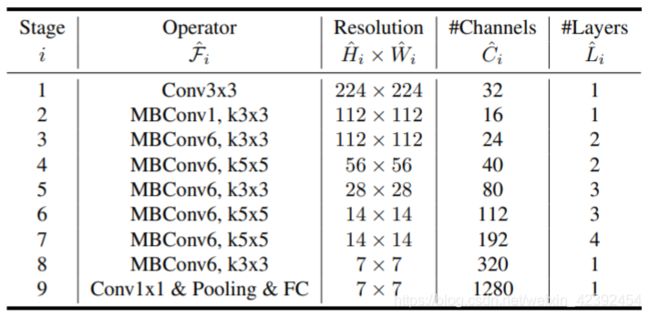
作者在已有的MobileNets和ResNets上证明了复合缩放的方式表现的很好,而且模型缩放后的准确率很大程度依赖于baseline网络。所以作者使用NAS(神经网络搜索)搜索出一个更好的baseline网络,也即EfficientNet-B0。
Efficient block
总体设计思路很简单先用1x1的卷积升维,在深度可分离卷积操作后添加一个注意力机制(SENet),最后再利用1x1卷积降维后,与输出合并。就是结合了之前各种网络的优点而已。
EfficientNet
最终将这几个Block重复多次叠加构成EfficientNet
4、实验结果
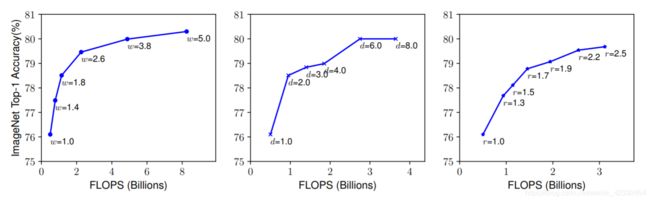
作者首先分别缩放 w , d , r w,d,r w,d,r的值,往往放大可以获得更高的精度,但准去了上升到80%之后就会迅速饱和,这表明了只对单一维度进行扩张十有局限性的。
随后作者尝试了复合缩放的方法,直观来说,对于更大分辨率的图像,我们应该增加网络的深度,这样才能有更大的感受野有助于在包含更多像素的更大的图像中捕捉相似的特征。相应的,当分辨率更高的时候,我们应该也增加网络的宽度,在有更多像素的高分辨率图像中捕捉更多细粒度的图案。这意味着我们需要配合且平衡不同维度的缩放,而不是传统的单个维度的缩放。
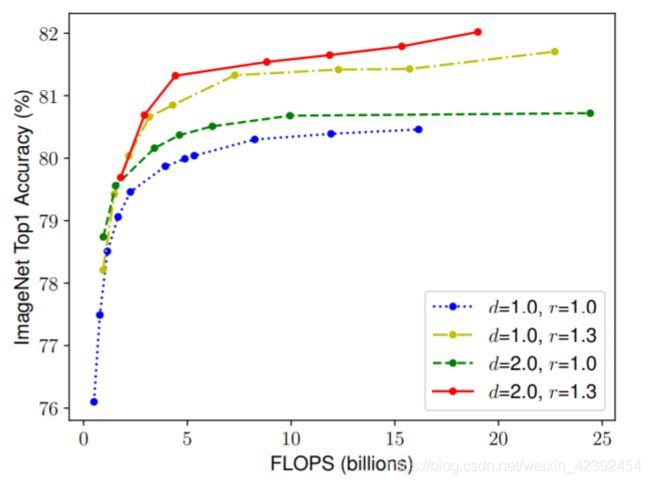
为了验证这个想法,作者对比了在不同网络深度和分辨率下缩放宽度的结果,如下图所示。如果只是缩放网络宽度 w w w,而不改变深度( d = 1.0 d=1.0 d=1.0)和分辨率( r = 1.0 r=1.0 r=1.0),准确率就会很快饱和。而在更深( d = 2.0 d=2.0 d=2.0)和更高分辨率( r = 2.0 r=2.0 r=2.0),缩放网络的宽度在相同的计算量下达到了更好的准确率。
5、结论
基于上述的实验结果,论文提出了一个新的复合缩放方法,使用一个复合系数 ϕ \phi ϕ来一致的缩放网络的宽度,深度和分辨率用一个规定的方式
定义:
d e p t h : d = α ϕ w i d t h : w = β ϕ r e s o l u t i o n : r = γ ϕ depth: d=\alpha^\phi\\ width: w=\beta^\phi\\ resolution: r=\gamma^\phi\\ depth:d=αϕwidth:w=βϕresolution:r=γϕ
缩放系数的建议公式:
s . t . α ⋅ β 2 ⋅ γ 2 ≈ 2 α ≥ 1 , β ≥ 1 , γ ≥ 1 s.t. \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2\\ \alpha \geq 1, \beta \geq1, \gamma\geq1 s.t.α⋅β2⋅γ2≈2α≥1,β≥1,γ≥1
所以对于任何新的 ϕ \phi ϕ总共的运算量将大约增加 2 ϕ 2^\phi 2ϕ
- Keras-EfficientNet