【机器学习】笔记5:Logistic Regression 逻辑斯蒂回归
Logistic Regression
- Reference
- Preparation
-
- 1. Regression and Classification
- 2. Generative Models and Discriminant Models for Classification
- 3. Naive Bayes
- 4. Hyperplane
- 5. Information Theory
- Notations
- Logistic Regression
- 1. What is Logistic Regression ?
- 2. Why Logistic Regression ?
-
- 2.1 why not linear regression for classification?
- 2.2 why not squared error ?
- 3. How Logistic Regression ?
- 4.Multi-classification
- 5.to be continued...
Reference
机器学习技法课–台湾大学 林轩田
机器学习–周志华
统计学习方法–李航
PRML
ESL
MLAPP
Preparation
You need to learn about those disgusting stuff below.
1. Regression and Classification
参考台湾大学林轩田老师机器学习基石:Learning Types和李航老师的统计学习指导。
| Regression | Classification | |
|---|---|---|
| Our Mission | 预测 输入变量和输出变量之间的数值型关系; | 预测 输入变量的所属类别 C k , k = 1 , 2 , . . , K C_k, \;k=1,2,..,K Ck,k=1,2,..,K |
| 输入空间 | 可以是连续型,也可以是离散的 | 可以是连续型,也可以是离散的 |
| 输出空间 | 整个实数空间 | 输出变量的取值有限,离散 |
| 举例 | 线性回归 | 逻辑斯蒂回归 |
2. Generative Models and Discriminant Models for Classification
参考PRML: Linear Models for Classification.
生成模型
p ( C k ∣ x ) = p ( x ∣ C k ) p ( C k ) p ( x ) p(C_k|x)=\frac{p(x|C_k)p(C_k)}{p(x)} p(Ck∣x)=p(x)p(x∣Ck)p(Ck)
- 根据数据得到先验的概率分布和变量的条件概率分布:
p ( x ∣ C k ) , p ( C k ) ← D a t a s e t p(x|C_k),p(C_k)\leftarrow Dataset p(x∣Ck),p(Ck)←Dataset
- 根据所得到的条件概率分布和先验分布,计算变量的概率分布:
p ( x ) ← p ( x ∣ C k ) , p ( C k ) p(x)\leftarrow p(x|C_k),p(C_k) p(x)←p(x∣Ck),p(Ck)
- 给新的数据 x n e w x_{new} xnew, 计算其属于类别 k k k的后验概率,
即:
p ( C k ∣ x = x n e w ) = p ( x = x n e w , C k ) p ( x ) = p ( x = x n e w ∣ C k ) p ( C k ) p ( x ) = p ( x = x n e w ∣ C k ) p ( C k ) ∑ p ( x = x n e w ∣ C k ) p ( C k ) p(C_k|x=x_{new})=\frac{p(x=x_{new},C_k)}{p(x)}\\[2ex]= \frac{p(x=x_{new}|C_k)p(C_k)}{p(x)}\\[2ex]=\frac{p(x=x_{new}|C_k)p(C_k)}{\sum{p(x=x_{new}|C_k)p(C_k)}}\\[2ex] p(Ck∣x=xnew)=p(x)p(x=xnew,Ck)=p(x)p(x=xnew∣Ck)p(Ck)=∑p(x=xnew∣Ck)p(Ck)p(x=xnew∣Ck)p(Ck)
判别模型
- 根据数据建立后验概率分布,直接建立标签类别和输入变量之间的映射关系:
p ( C k ∣ x ) ← D a t a s e t p(C_k|x)\leftarrow Dataset p(Ck∣x)←Dataset - 给新的数据 x n e w x_{new} xnew, 直接给出其属于类别 k k k的后验概率:
p ( C k ∣ x = x n e w ) p(C_k|x=x_{new}) p(Ck∣x=xnew)
比较
| 分类问题 | 生成模型 | 判别模型 |
|---|---|---|
| 方法 | 通过数据学习 得到联合概率分布 P ( x , C k ) P(x,C_k) P(x,Ck) | 通过数据学习 得到条件分布$P(C_k |
| 优点 | 1)可以还原出联合分布概率;;2)收敛速度更快,当数据量增加时,学习模型的速度更快,收敛于真实模型;3)含有隐变量时仍可用 | 1)学习的准确率更高;2)简化学习问题 |
注:生成模型,可以还原出联合概率的分布哦。
3. Naive Bayes
参考李航老师的统计学习指导一书。
朴素贝叶斯法通过训练数据学习联合分布 P ( X , Y ) P(X,Y) P(X,Y), 具体如下:
-
学习先验分布
P ( Y = C k ) , k = 1 , 2 , . . , K P(Y=C_k),\; k=1,2,..,K P(Y=Ck),k=1,2,..,K -
学习条件分布概率
P ( X = x n ∣ Y = C k ) = P ( X ( 1 ) = x n ( 1 ) , X ( 2 ) = x n ( 2 ) , . . . , X ( d ) = x n ( d ) ∣ Y = C k ) P(X=x_n|Y=C_k)=P(X^{(1)}=x_n^{(1)},X^{(2)}=x_n^{(2)},...,X^{(d)}=x_n^{(d)}|Y=C_k) P(X=xn∣Y=Ck)=P(X(1)=xn(1),X(2)=xn(2),...,X(d)=xn(d)∣Y=Ck)
需要估计的参数个数为: ( K ∏ i = 1 d S i ) − 1 (K\prod_{i=1}^{d}S_i)-1 (K∏i=1dSi)−1,指数量级。 -
plus 条件独立性假设
P ( X = x n ∣ Y = C k ) = ∏ P ( X i = x n i ∣ Y = C k ) P(X=x_n|Y=C_k)=\prod P(X^i=x_n^i|Y=C_k) P(X=xn∣Y=Ck)=∏P(Xi=xni∣Y=Ck)
需要估计的参数个数为: K ( ∏ i = 1 d S i − 1 ) K(\prod_{i=1}^{d} S_i-1) K(∏i=1dSi−1),依然指数量级。 -
给新的数据 x n e w x_{new} xnew, 计算其属于类别 k k k的后验概率:
p ( Y = C k ∣ x = x n e w ) = p ( x = x n e w ∣ C k ) p ( Y = C k ) ∑ p ( x = x n e w ∣ C k ) p ( Y = C k ) p(Y=C_k|x=x_{new})=\frac{p(x=x_{new}|C_k)p(Y=C_k)}{\sum{p(x=x_{new}|C_k)p(Y=C_k)}}\\[2ex] p(Y=Ck∣x=xnew)=∑p(x=xnew∣Ck)p(Y=Ck)p(x=xnew∣Ck)p(Y=Ck) -
将后验概率最大的类作为 x n e w x_{new} xnew的类别输出:
y = f ( x n e w ) = a r g m a x C k p ( x = x n e w ∣ C k ) p ( Y = C k ) ∑ p ( x = x n e w ∣ C k ) p ( Y = C k ) y=f(x_{new})=arg\,max_{C_k}\frac{p(x=x_{new}|C_k)p(Y=C_k)}{\sum{p(x=x_{new}|C_k)p(Y=C_k)}}\\[2ex] y=f(xnew)=argmaxCk∑p(x=xnew∣Ck)p(Y=Ck)p(x=xnew∣Ck)p(Y=Ck)
附注:
拉普拉斯平滑:lambda=1.
在随机变量的各个特征的取值上面,赋予一个基本的正数 lambda,通常取1.
引入原因:训练集中某特征的属性取值可能不全面。
缺点:假设了属性取值和类别是均匀分布的,相当于额外引入了关于数据的先验。
假设训练集合里西瓜颜色的取值为:{绿色,白色},
为了避免新的样本出现时,若有Prob(颜色=红色,瓜=好瓜)=0,出现联合概率乘积为0的情况:
可以记#(颜色=红色,瓜=好瓜)=1, 同时使得#(颜色=绿色,瓜=好瓜)增加1,#(颜色=绿色,瓜=好瓜)增加1.
4. Hyperplane
参考PRML和网络blogs,距离计算部分详见SVM Part1。
超平面指的是从n维空间到n-1维空间的一个映射子空间,表达式:
w T x + b = 0 o r : w T x + w 0 = 0 w^Tx+b=0\\[2ex] \blue {or:}{ \; w^Tx+w_0=0} wTx+b=0or:wTx+w0=0
在分类问题中,利用这样的超平面,可以将特征空间中的点划分开来,具体方式:
s i g n ( w T x + b ) = { + 1 w x + b ≥ 0 − 1 w x + b < 0 sign(w^Tx+b)=\left\{ \begin{array}{rcl} +1 & & {wx+b\geq 0}\\ -1 & & {wx+b< 0}\\ \end{array} \right. sign(wTx+b)={+1−1wx+b≥0wx+b<0
以三维空间为例,其超平面为二维平面。
记 x A x_A xA为超平面上一点,
x 外 x_外 x外为超平面外一点,
( x 外 − x A ) ({x}_外-x_A) (x外−xA)与超平面的法向量 w w w的夹角记为 θ \theta θ,
d d d 为超平面外一点到超平面的距离;
可得:
∣ w T • ( x 外 − x A ) ∣ = ∣ ∣ w ∣ ∣ • ∣ ∣ x 外 − x A ∣ ∣ • c o s θ |w^T•({x}_外-x_A)|=||w||•||{x}_外-x_A||•cos\theta ∣wT•(x外−xA)∣=∣∣w∣∣•∣∣x外−xA∣∣•cosθ
∣ ∣ x 外 − x A ∣ ∣ • c o s θ = d ||{x}_外-x_A||•cos\theta=d ∣∣x外−xA∣∣•cosθ=d
w T x A + b = 0 w^Tx_A+b=0 wTxA+b=0
则超平面外一点到超平面的距离:
d = ∣ w T • ( x 外 − x A ) ∣ ∣ ∣ w ∣ ∣ = ∣ w T • x 外 + b ∣ ∣ ∣ w ∣ ∣ d=\frac{|w^T•({x}_外-x_A)|}{||w||}=\frac{|w^T•{x}_外+b |}{||w||} d=∣∣w∣∣∣wT•(x外−xA)∣=∣∣w∣∣∣wT•x外+b∣
5. Information Theory
参考PRML,MLAPP和统计学习指导
entropy
考虑一个离散的随机变量 x x x,信息量可以描述为看到这个随机变量的具体取值时的“惊讶程度”。
直觉上,如果两个事件 x , y x,y x,y不相关,那么观察到这两个事件同时发生的时候获得的信息量程度应该等于观察到这两个事件各自发生时的信息量之和。用 h ( • ) h(•) h(•)表示事件的信息量, h ( x , y ) = h ( x ) + h ( y ) h(x,y)=h(x)+h(y) h(x,y)=h(x)+h(y). 两个事件不相关,相当于其相互独立,所以 p ( x , y ) = p ( x ) • p ( y ) p(x,y)=p(x)•p(y) p(x,y)=p(x)•p(y).
易得, h ( • ) h(•) h(•)采用的是取对数的形式: h ( x ) = − l o g 2 p ( x ) h(x)=-log_2\,p(x) h(x)=−log2p(x)
假设一个人想要将随机变量 x x x的取值发送给其接收者,则这个过程的平均信息量可以通过 h ( x ) h(x) h(x)的概率分布求得:
H ( x ) = ∑ x p ( h ( x ) ) • h ( x ) = − ∑ x p ( x ) • l o g 2 p ( x ) H(x)=\sum \limits_{x} p(h(x))•h(x)=-\sum \limits_{x} p(x)•log_2\,p(x) H(x)=x∑p(h(x))•h(x)=−x∑p(x)•log2p(x)
称之为随机变量 x x x的熵。
以服从伯努利分布的随机变量x为例,x取值为0/1.
| x = 1 x=1 x=1 | x = 0 x=0 x=0 | |
|---|---|---|
| p r o b ( x ) prob(x) prob(x) | p p p | 1 − p 1-p 1−p |
| p r o b ( h ( x ) ) prob(h(x)) prob(h(x)) | p p p | 1 − p 1-p 1−p |
易得 p = 1 → p • l o g 2 p = 0 p=1 \rightarrow p\,•\,log_2\,p=0 p=1→p•log2p=0,如果某一件事情一定会发生,那么这个观测相当于没有产生信息。
记 p = 0 , p • l o g 2 p = 0 p=0,\;p\,•\,log_2\,p=0 p=0,p•log2p=0,如果 x x x的某取值几乎为不可能事件,结果发生了,虽然观测到这一情况会“很惊讶”,但我们也认为其信息量为0.
N o t e t h a t : h ( x ) = l o g 2 ( p r o b ( x ) ) \red{Note \; that:h(x)=log_2(prob(x))} Notethat:h(x)=log2(prob(x))
物理角度
考虑一个集合,包含 N N N个完全相同的物体,要将这些物体分配到若干个箱子中,使得第 i i i个箱子里面有 n i n_i ni个物体,不考虑各个箱子内物体的排列组合,则方案总数 W W W为:
W = N ! ∏ i n i ! W=\frac{N!}{\prod \limits_{i}n_i!} W=i∏ni!N!
将其称之为multiplicity, 对其取对数之后进行适当的参数放缩后的结果定义为熵,单位为nat.
H = 1 N ln W = 1 N ln N ! − 1 N ∑ i ln n i ! H=\frac{1}{N}\ln W=\frac{1}{N}\ln N!-\frac{1}{N}\sum\limits_{i}\ln n_i! H=N1lnW=N1lnN!−N1i∑lnni!
N → ∞ N\rightarrow \infty N→∞,by ln N ! ≈ N ln N − N \ln N!\approx N\ln N-N lnN!≈NlnN−N
H = − lim N → ∞ ∑ ( n i N ) ln ( n i N ) = − ∑ i p i ln p i H=-\mathop{\lim}\limits_{N\rightarrow \infty}\sum\bigg(\frac{n_i}{N}\bigg) \ln\bigg( \frac{n_i}{N} \bigg)=-\sum_{i}p_i\ln p_i H=−N→∞lim∑(Nni)ln(Nni)=−i∑pilnpi
Proof:
H = 1 N ln N ! − 1 N ∑ i ln n i ! = 1 N ( N ln N − N ) − 1 N ∑ i ( n i ln n i − n i ) = ln N − 1 − 1 N ∑ i n i ln n i + 1 N ∑ i n i = 1 N ∑ n i ln N − 1 N ∑ i n i ln n i = − ∑ i ( n i N ) ln ( n i N ) = − ∑ i p i ln p i \begin{aligned} H=&\frac{1}{N}\ln N!-\frac{1}{N}\sum\limits_{i}\ln n_i!\\ =&\frac{1}{N}( N\ln N-N)-\frac{1}{N}\sum\limits_{i}({n_i}\ln {n_i}-n_i)\\ =&\ln N-1-\frac{1}{N}\sum\limits_{i}{n_i}\ln {n_i}+\frac{1}{N}\sum_in_i\\ =&\frac{1}{N}\sum n_i\ln N-\frac{1}{N}\sum\limits_{i}{n_i}\ln {n_i}\\ =&-\sum_i\bigg(\frac{n_i}{N}\bigg) \ln\bigg( \frac{n_i}{N} \bigg)\\ =&-\sum_{i}p_i\ln p_i \end{aligned} H======N1lnN!−N1i∑lnni!N1(NlnN−N)−N1i∑(nilnni−ni)lnN−1−N1i∑nilnni+N1i∑niN1∑nilnN−N1i∑nilnni−i∑(Nni)ln(Nni)−i∑pilnpi
entropy increased:
- 信息量⬆️
- distribution: spread⬆️
- impurity⬆️
cross entropy
y y y 服从二项分布, p ( y = 1 ) = 2 / 5 , p ( y = 0 ) = 3 / 5 p(y=1)=2/5,p(y=0)=3/5 p(y=1)=2/5,p(y=0)=3/5
| y i y_i yi | 0 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|
| p ( y i = 0 ) p(y_i=0) p(yi=0) | 1 | 1 | 0 | 1 | 0 |
| p ( y i = 1 ) p(y_i=1) p(yi=1) | 0 | 0 | 1 | 0 | 1 |
q i = q ( y i = 1 ∣ x i ) = s i g m o i d ( w T x i + b ) q_i=q(y_i=1|x_i)=sigmoid(w^Tx_i+b) qi=q(yi=1∣xi)=sigmoid(wTxi+b)
w h e n y i = 1 , p i = p ( y i = 1 ) ; w h e n y i = 0 , p i = p ( y i = 0 ) when \; y_i=1,p_i=p(y_i=1);when \; y_i=0,p_i=p(y_i=0) whenyi=1,pi=p(yi=1);whenyi=0,pi=p(yi=0)
∑ y i log ( q i ) + ( 1 − y i ) log ( 1 − q i ) = ∑ ( y i ∣ y i = 1 ) y i log ( q i ) + ∑ ( y i ∣ y i = 0 ) ( 1 − y i ) log ( 1 − q i ) ( y i = 0 , 前 一 项 为 0 ; y i = 1 时 , 后 一 项 为 0 ) = ∑ [ p ( y i = 1 ) log ( q i ) + ( 1 − p ( y i = 1 ) ) log ( 1 − q i ) ] = ∑ [ p i log ( q i ) + ( 1 − p i ) log ( 1 − q i ) ] \begin{aligned} \sum y_i\log (q_i)+(1-y_i)\log (1-q_i) =& \sum_ {(y_i|y_i=1)}y_i\log (q_i)+\sum_ {(y_i|y_i=0)}(1-y_i)\log (1-q_i)\;\;\red{(y_i=0,前一项为0;y_i=1时,后一项为0)}\\ =&\sum [ p(y_i=1)\log (q_i)+ ({1-p(y_i=1)})\log (1-q_i)]\\ =&\sum [ p_i\log (q_i)+ ({1-p_i})\log (1-q_i)]\\ \end{aligned} ∑yilog(qi)+(1−yi)log(1−qi)===(yi∣yi=1)∑yilog(qi)+(yi∣yi=0)∑(1−yi)log(1−qi)(yi=0,前一项为0;yi=1时,后一项为0)∑[p(yi=1)log(qi)+(1−p(yi=1))log(1−qi)]∑[pilog(qi)+(1−pi)log(1−qi)]
Notations
- 训练数据集:{ ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) (x_1,y_1),(x_2,y_2),...,(x_N,y_N) (x1,y1),(x2,y2),...,(xN,yN)}
- 输出空间:{ C 1 , C 2 , . . . , C K C_1,C_2,...,C_K C1,C2,...,CK}
- 输入空间上: x n = ( x n ( 1 ) , x n ( 2 ) , . . . , x n ( d ) ) x_n=(x_n^{(1)},x_n^{(2)},...,x_n^{(d)}) xn=(xn(1),xn(2),...,xn(d))
- 自变量: d d d 个维度,每个维度上的取值为 S i S_i Si 个
- 输入空间上: x n ( i ) x_n^{(i)} xn(i), 第 n n n个样本, 第 i i i个维度(特征)
Logistic Regression
1. What is Logistic Regression ?
参考PRML,统计学习指导和台湾大学李宏毅老师 Machine Learning课程。
先讨论二分类的情况。
Logistic Regression是一种分类模型,由条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)表示:
P ( Y = 1 ∣ x ) = 1 1 + e − ( w T x + w 0 ) P(Y=1|x)=\frac{1}{1+e^{-(w^Tx+w_0)}} P(Y=1∣x)=1+e−(wTx+w0)1
其中,
s i g m o i d ( a ) = 1 1 + e − a ln P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = w T x + w 0 sigmoid(a)=\frac{1}{1+e^{-a}} \\[2ex]\\ \ln \frac{P(Y=1|x)}{1-P(Y=1|x)}=w^Tx+w_0 sigmoid(a)=1+e−a1ln1−P(Y=1∣x)P(Y=1∣x)=wTx+w0
2. Why Logistic Regression ?
将线性判别函数记为输入向量 的线性函数:
f ( x ) = s i g n ( w T x + b ) f(x)=sign(w^Tx+b) f(x)=sign(wTx+b)
s i g n ( w T x + b ) = { + 1 w T x + b ≥ 0 − 1 w T x + b < 0 sign(w^Tx+b)=\left\{ \begin{array}{rcl} +1 & & {w^Tx+b\geq 0}\\ -1 & & {w^Tx+b< 0}\\ \end{array} \right. sign(wTx+b)={+1−1wTx+b≥0wTx+b<0
记 w T = ( w 0 , w T ) , x T = ( 1 , x T ) w^T=(w_0,w^T),x^T=(1,x^T) wT=(w0,wT),xT=(1,xT),简化上式为
s i g n ( w T x ) = { + 1 w T x ≥ 0 − 1 w T x < 0 sign(w^Tx)=\left\{ \begin{array}{rcl} +1 & & {w^Tx\geq 0}\\ -1 & & {w^Tx< 0}\\ \end{array} \right. sign(wTx)={+1−1wTx≥0wTx<0
-
判别模型 or 生成模型:
判别模型 “?”: less parameters to be estimated, less assumption
举例:
在贝叶斯生成模型中,
连续性输入时,假设类条件概率 p ( x ∣ y ∈ C k ) p(x|y\in C_k) p(x∣y∈Ck)服从高斯分布;
离散型输入时,作条件独立假设,将参数估计的指数量级 ( ∏ K ⋅ S j ) − 1 (\prod K·S_j)-1 (∏K⋅Sj)−1减少至 ∑ K ⋅ ( S j − 1 ) \sum K·(S_j-1) ∑K⋅(Sj−1) .
( K K K表示输出空间熵 y y y的标签种类数, S j S_j Sj表示输入空间上,第 j j j个特征的取值数目。此处符号表示参见李航老师的统计学习指导) -
输出概率形式 or 0/1 形式:
输出概率 “?”:still available for multi-classification
举例:
以感知机为例,其可以处理二分类问题(X线性可分时), s i g n ( w T + b ) ≥ 0 → y = 1 ; v i c e v e r s a sign(w^T+b)\geq0 \rightarrow y=1;vice\;versa sign(wT+b)≥0→y=1;viceversa当处理多分类问题时,
若采用1 of K (OVR)的方法,用K-1个分类器将输入空间划分为不同的决策区域,可能会出现多个决策区域重叠的情况,从而产生无法分类的情况。
即使若采用2 of K (OVO)的方法,用 C K 2 C_K^2 CK2个分类器将输入空间划分为不同的决策区域,也会产生无法分类的情况。

-
线性回归 or logistic 回归:
logistic回归 “?”:可输出概率形式 ∈ [ 0 , 1 ] \in [0,1] ∈[0,1];多分类时可采用softmax(OVO to OVR) -
squared loss or cross-entropy (MLE):
cross-entropy (MLE) “?”: more robust for outliers; 梯度下降优化时,效率更高
2.1 why not linear regression for classification?
mission:new x i x_i xi given,ouput p ( y i = 1 ∣ x i ) p(y_i=1|x_i) p(yi=1∣xi)
模型:linear regression
损失函数:squared loss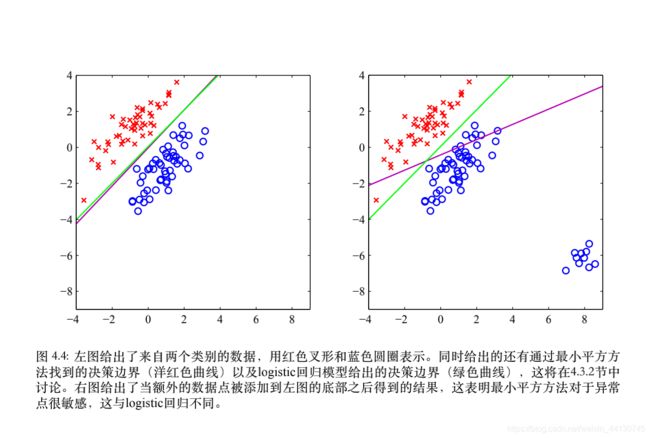
问题:
- 最小平方法:not robust, 对于异常点较为敏感,如上图所示
- 输出空间:模型输出不一定为概率形式,out of [ 0 , 1 ] [0,1] [0,1]
- 假设不符:最小平方法对应高斯分布假设下的最大似然方法,但此处 y y y并不属于高斯分布
2.2 why not squared error ?
mission:new x i x_i xi given,ouput p ( y i = 1 ∣ x i ) p(y_i=1|x_i) p(yi=1∣xi)
模型:logistic regression
损失函数:squared loss

问题:
- 采用梯度下降法求解时,效率低
损失函数对 w i w_i wi求偏导得: 2 ( p ( y i = 1 ∣ x i ) − y i ) ⋅ p ( y i = 1 ∣ x i ) ⋅ ( 1 − p ( y i = 1 ∣ x i ) ) \big(p(y_i=1|x_i)-y_i\big)·p(y_i=1|x_i)·\big(1-p(y_i=1|x_i)\big) (p(yi=1∣xi)−yi)⋅p(yi=1∣xi)⋅(1−p(yi=1∣xi))
具体表现为:
y i = 0 y_i=0 yi=0时,若predict probability p ( y i = 1 ∣ x i ) p(y_i=1|x_i) p(yi=1∣xi)接近于1,第三项接近于0,则梯度接近于0
y i = 0 y_i=0 yi=0时,若predict probability接近于0,梯度也接近于0 - 最小平方法:同样的not robust, 对于异常点较为敏感
3. How Logistic Regression ?
4.Multi-classification
参考PRML & ESL.
假设我们有多(K>2)个类别
mission: 判断 y i ∣ x i y_i|x_i yi∣xi所属类别 ⬅️ 给出 p ( y i ∈ C k ∣ x i ) , k = [ 1 , 2 , . . . , K ] p(y_i \in C_k|x_i),k=[1,2,...,K] p(yi∈Ck∣xi),k=[1,2,...,K]的所有概率值 ⬅️ 用(K-1)个二元logistic regression 分类器输出概率,再作归一化处理。
Details:
判断 y i ∣ x i y_i|x_i yi∣xi所属类别⬅️ 给出 p ( y i ∈ C k ∣ x i ) , k = [ 1 , 2 , . . . , K ] p(y_i \in C_k|x_i),k=[1,2,...,K] p(yi∈Ck∣xi),k=[1,2,...,K]的所有概率值。
计算 p ( y i ∈ C 1 ∣ x i ) p(y_i \in C_1|x_i) p(yi∈C1∣xi)
log p ( y i ∈ C 1 ∣ x i ) p ( y i ∈ C 1 ∣ x i ) = w 1.1 T x → n u l l ? → p ( y i ∈ C 1 ∣ x i ) = 1 − p ( y i ∉ C 1 ∣ x i ) log p ( y i ∈ C 2 ∣ x i ) p ( y i ∈ C 1 ∣ x i ) = w 1.2 T x → p ( y i ∈ C 1 ∣ x i ) = exp ( − w 1.2 T x ) 1 + exp ( − w 1.2 T x ) = 1 1 + exp ( w 1.2 T x ) log p ( y i ∈ C 3 ∣ x i ) p ( y i ∈ C 1 ∣ x i ) = w 1.3 T x → p ( y i ∈ C 1 ∣ x i ) = exp ( − w 1.3 T x ) 1 + exp ( − w 1.3 T x ) = . . . . . . log p ( y i ∈ C K ∣ x i ) p ( y i ∈ C 1 ∣ x i ) = w 1. K T x → p ( y i ∈ C 1 ∣ x i ) = exp ( − w 1. K T x ) 1 + exp ( − w 1. K T x ) = . . . \log \frac{p(y_i \in C_1|x_i)}{p(y_i \in C_1|x_i)}=w_{1.1}^Tx \rightarrow \red {null?}\rightarrow p(y_i \in C_1|x_i)=1- p(y_i \notin C_1|x_i)\\[2ex] \log \frac{p(y_i \in C_2|x_i)}{p(y_i \in C_1|x_i)}=w_{1.2}^Tx \rightarrow p(y_i \in C_1|x_i)=\frac{\exp(-w_{1.2}^Tx )}{1+\exp(-w_{1.2}^Tx )} =\frac{1}{1+\exp(w_{1.2}^Tx )}\\[2ex] \log \frac{p(y_i \in C_3|x_i)}{p(y_i \in C_1|x_i)}=w_{1.3}^Tx \rightarrow p(y_i \in C_1|x_i)=\frac{\exp(-w_{1.3}^Tx )}{1+\exp(-w_{1.3}^Tx )}=...\\[2ex] ...\\[2ex] \log \frac{p(y_i \in C_K|x_i)}{p(y_i \in C_1|x_i)}=w_{1.K}^Tx \rightarrow p(y_i \in C_1|x_i)=\frac{\exp(-w_{1.K}^Tx )}{1+\exp(-w_{1.K}^Tx )}=...\\[2ex] logp(yi∈C1∣xi)p(yi∈C1∣xi)=w1.1Tx→null?→p(yi∈C1∣xi)=1−p(yi∈/C1∣xi)logp(yi∈C1∣xi)p(yi∈C2∣xi)=w1.2Tx→p(yi∈C1∣xi)=1+exp(−w1.2Tx)exp(−w1.2Tx)=1+exp(w1.2Tx)1logp(yi∈C1∣xi)p(yi∈C3∣xi)=w1.3Tx→p(yi∈C1∣xi)=1+exp(−w1.3Tx)exp(−w1.3Tx)=......logp(yi∈C1∣xi)p(yi∈CK∣xi)=w1.KTx→p(yi∈C1∣xi)=1+exp(−w1.KTx)exp(−w1.KTx)=...
左右两边(K-1项)分别求和:
p ( y i ∈ C 2 ∣ x i ) p ( y i ∈ C 1 ∣ x i ) + . . . + p ( y i ∈ C K ∣ x i ) p ( y i ∈ C 1 ∣ x i ) = ∑ k = 2 K exp ( w 1. k T x ) ∑ k = 1 K p ( y i ∈ C k ∣ x i ) p ( y i ∈ C 1 ∣ x i ) − p ( y i ∈ C 1 ∣ x i ) p ( y i ∈ C 1 ∣ x i ) = ∑ k = 2 K exp ( w 1. k T x ) ∑ k = 1 K p ( y i ∈ C k ∣ x i ) p ( y i ∈ C 1 ∣ x i ) = ∑ k = 2 K exp ( w 1. k T x ) + 1 p ( y i ∈ C 1 ∣ x i ) ∑ k = 1 K p ( y i ∈ C k ∣ x i ) = 1 1 + ∑ k = 2 K exp ( w 1. k T x ) \frac{p(y_i \in C_2|x_i)}{p(y_i \in C_1|x_i)}+...+ \frac{p(y_i \in C_K|x_i)}{p(y_i \in C_1|x_i)}=\sum_{k=2}^{K} \exp (w_{1.k}^Tx)\\[2ex] \frac{\sum_{k=1}^{K}p(y_i \in C_k|x_i)}{p(y_i \in C_1|x_i)}-\frac{p(y_i \in C_1|x_i)}{p(y_i \in C_1|x_i)}=\sum_{k=2}^{K} \exp (w_{1.k}^Tx)\\[2ex] \frac{\sum_{k=1}^{K}p(y_i \in C_k|x_i)}{p(y_i \in C_1|x_i)}=\sum_{k=2}^{K} \exp (w_{1.k}^Tx)+1\\[2ex] \frac{p(y_i \in C_1|x_i)}{\sum_{k=1}^{K}p(y_i \in C_k|x_i)}=\frac{1}{1+\sum_{k=2}^{K} \exp (w_{1.k}^Tx)}\\[2ex] p(yi∈C1∣xi)p(yi∈C2∣xi)+...+p(yi∈C1∣xi)p(yi∈CK∣xi)=k=2∑Kexp(w1.kTx)p(yi∈C1∣xi)∑k=1Kp(yi∈Ck∣xi)−p(yi∈C1∣xi)p(yi∈C1∣xi)=k=2∑Kexp(w1.kTx)p(yi∈C1∣xi)∑k=1Kp(yi∈Ck∣xi)=k=2∑Kexp(w1.kTx)+1∑k=1Kp(yi∈Ck∣xi)p(yi∈C1∣xi)=1+∑k=2Kexp(w1.kTx)1
同样地,计算 p ( y i ∈ C 2 ∣ x i ) p(y_i \in C_2|x_i) p(yi∈C2∣xi)
log p ( y i ∈ C 1 ∣ x i ) p ( y i ∈ C 2 ∣ x i ) = w 2.1 T x → p ( y i ∈ C 2 ∣ x i ) = exp ( − w 2.1 T x ) 1 + exp ( − w 2.1 T x ) log p ( y i ∈ C 2 ∣ x i ) p ( y i ∈ C 2 ∣ x i ) = w 2.2 T x → n u l l ? → p ( y i ∈ C 2 ∣ x i ) = 1 − p ( y i ∉ C 2 ∣ x i ) log p ( y i ∈ C 3 ∣ x i ) p ( y i ∈ C 2 ∣ x i ) = w 2.3 T x → p ( y i ∈ C 2 ∣ x i ) = exp ( − w 2.3 T x ) 1 + e x p ( − w 2.3 T x ) . . . log p ( y i ∈ C K ∣ x i ) p ( y i ∈ C 2 ∣ x i ) = w 2. K T x → p ( y i ∈ C 2 ∣ x i ) = exp ( − w 2. K T x ) 1 + e x p ( − w 2. K T x ) \log \frac{p(y_i \in C_1|x_i)}{p(y_i \in C_2|x_i)}=w_{2.1}^Tx \rightarrow p(y_i \in C_2|x_i)=\frac{\exp(-w_{2.1}^Tx )}{1+\exp(-w_{2.1}^Tx )}\\[2ex] \log \frac{p(y_i \in C_2|x_i)}{p(y_i \in C_2|x_i)}=w_{2.2}^Tx \rightarrow \red {null?}\rightarrow p(y_i \in C_2|x_i)=1- p(y_i \notin C_2|x_i) \\[2ex] \log \frac{p(y_i \in C_3|x_i)}{p(y_i \in C_2|x_i)}=w_{2.3}^Tx \rightarrow p(y_i \in C_2|x_i)=\frac{\exp(-w_{2.3}^Tx )}{1+exp(-w_{2.3}^Tx )}\\[2ex] ...\\[2ex] \log \frac{p(y_i \in C_K|x_i)}{p(y_i \in C_2|x_i)}=w_{2.K}^Tx \rightarrow p(y_i \in C_2|x_i)=\frac{\exp(-w_{2.K}^Tx )}{1+exp(-w_{2.K}^Tx )}\\[2ex] logp(yi∈C2∣xi)p(yi∈C1∣xi)=w2.1Tx→p(yi∈C2∣xi)=1+exp(−w2.1Tx)exp(−w2.1Tx)logp(yi∈C2∣xi)p(yi∈C2∣xi)=w2.2Tx→null?→p(yi∈C2∣xi)=1−p(yi∈/C2∣xi)logp(yi∈C2∣xi)p(yi∈C3∣xi)=w2.3Tx→p(yi∈C2∣xi)=1+exp(−w2.3Tx)exp(−w2.3Tx)...logp(yi∈C2∣xi)p(yi∈CK∣xi)=w2.KTx→p(yi∈C2∣xi)=1+exp(−w2.KTx)exp(−w2.KTx)
左右两边分别求和:
. . . ... ...
因为
log p ( y i ∈ C 1 ∣ x i ) p ( y i ∈ C 2 ∣ x i ) \log \frac{p(y_i \in C_1|x_i)}{p(y_i \in C_2|x_i)} logp(yi∈C2∣xi)p(yi∈C1∣xi)和 log p ( y i ∈ C 2 ∣ x i ) p ( y i ∈ C 1 ∣ x i ) \log \frac{p(y_i \in C_2|x_i)}{p(y_i \in C_1|x_i)} logp(yi∈C1∣xi)p(yi∈C2∣xi)对称,所以只需要训练 K ( K − 1 ) 2 − 1 \frac{K(K-1)}{2}-1 2K(K−1)−1个logistic分类器即可。