机器学习——L1和L2正则化对回归模型的影响
《机器学习:公式推导与代码实践》鲁伟著读书笔记。
回归模型拓展
对于回归模型来说,目标变量有许多影响因素。但是这么多影响因素之中,总有少数关键因素对目标变量的变化起着重要的影响。面对过多影响因素的回归模型来说,若仅仅采用传统的回归模型对其进行求解的话,拟合效果不尽如人意。针对这种情况,LASSO回归和Ridge回归模型便可以来解决影响因素较多的回归问题。
LASSO回归原理推导
LASSO回归模型又可以称之为最小绝对收缩和选择算子回归模型。但是为什么要用LASSO回归模型呢?我们要从“机器学习——线性回归模型及python代码实现”这一章开始分析。我们已经计算得到了权重的梯度: ∂ L ∂ ω = 2 X T ( X ω − y ) \frac{\partial L}{\partial {\omega}}=2X^{T}(X\omega-y) ∂ω∂L=2XT(Xω−y)若矩阵 X T X X^{T}X XTX为满秩矩阵或者是正定矩阵时,令上式等于0,可解得权重的更新公式为: ω ∗ = ( X T X ) − 1 X T y \omega ^{*}=(X^{T}X)^{-1}X^{T}y ω∗=(XTX)−1XTy但是如果假设不成立,训练样本的数量小于样本特征数,即 r a n k ( X ) < n rank(X)
针对这一问题,LASSO的做法便是在线性回归的损失函数后面加一个1-范数项,也叫正则化项,可以称之为L1正则化。新的损失函数的表达式为: L ( ω ) = ( y − X ω ) 2 + λ ∣ ∣ ω ∣ ∣ 1 L(\omega)=(y-X\omega)^{2}+\lambda ||\omega||_{1} L(ω)=(y−Xω)2+λ∣∣ω∣∣1其中 ∣ ∣ ω ∣ ∣ 1 ||\omega||_{1} ∣∣ω∣∣1即为矩阵的1-范数,也就是绝对值, λ \lambda λ为1-范数项系数,又称为正则化系数。
正则化相当于对目标参数施加了一个惩罚项,使得模型不能过于复杂,阻止模型过拟合。在优化过程中,正则化得存在能够使一些不重要的特征系数逐渐压缩为0,从而保存关键特征,在一定程度上起到降维的效果,使得模型得到了简化。所以上式等价于: arg min ( y − X ω ) 2 \text{arg } \text{min}(y-X\omega)^{2} arg min(y−Xω)2 s.t. Σ ∣ ω ∣ i j < s \text{s.t. } \Sigma|\omega|_{ij}s.t. Σ∣ω∣ij<s s.t. Σ ∣ ω ∣ i j < s \text{s.t. } \Sigma|\omega|_{ij}s.t. Σ∣ω∣ij<s为权重系数矩阵所有袁术绝对值之和要小于一个指定常数s,s取值越小,特征参数中被压缩到0的特征就会越多。以二维影响因素为例,LASSO回归的参数估计图为: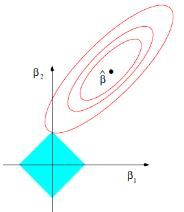
椭圆形区域为回归参数的求解空间,蓝色部分为L1正则化约束条件。
因为L1正则化项的存在使得新得到的目标函数无法进行求导计算,便无法使用梯度下降算法进行寻优。我们可以采用坐标下降法对LASSO回归寻优方法进行寻优,就无需计算目标函数的梯度。以二维空间为例,我们假设LASSO回归损失函数为L(x,y),此刻x,y为不同的权重。具体步骤如下:
Step1:我们先给定权重的初始点X0,寻找使L(y)达到最小的y参数的取值Y1。
Step2:固定Y1,寻找使L(x)达到最小的x参数的取值X1。
Step3:如果找到最优目标函数值,则x,y便是我们要寻找的最优参数。如果尚未找到,继续重复Step1和2。
Ridge回归原理推导
与LASSO回归模型相似,Ridge回归(岭回归)是一种使用2-范数作为惩罚项改造目标函数。Ridge回归的目标函数为: L ( ω ) = ( y − X ω ) 2 + λ ∣ ∣ ω ∣ ∣ 2 L(\omega)=(y-X\omega)^{2}+\lambda ||\omega||_{2} L(ω)=(y−Xω)2+λ∣∣ω∣∣2其中, λ ∣ ∣ ω ∣ ∣ 2 = λ Σ ω i 2 \lambda ||\omega||_{2}=\lambda \Sigma \omega_{i}^{2} λ∣∣ω∣∣2=λΣωi2,也叫L2正则化项。与L1正则化不一样的的是,L1正则化是将不重要的参数权重压缩为零,L2正则话是将其压缩至无限接近于0但不会等于0。如果正则化系数取值较大,参数矩阵中的每个元素都会变小,激活函数在相对较小的区间内呈线性状态,激活函数能够起到较好的激活效果,这样就会降低网络的深度,因而可以防止过拟合。目标函数可以等价于: arg min ( y − X ω ) 2 \text{arg } \text{min}(y-X\omega)^{2} arg min(y−Xω)2 s.t. Σ ω i j 2 < s \text{s.t. } \Sigma\omega^{2}_{ij}s.t. Σωij2<s为了能够使 X T X X^{T}X XTX可逆,在 X T X X^{T}X XTX后加上单位矩阵使其i变成非奇异矩阵并可以对其进行求逆操作。所以 ω ∗ = ( X T X ) − 1 X T y \omega ^{*}=(X^{T}X)^{-1}X^{T}y ω∗=(XTX)−1XTy可以改写为: ω ∗ = ( X T X + λ I ) − 1 X T y \omega ^{*}=(X^{T}X+\lambda I)^{-1}X^{T}y ω∗=(XTX+λI)−1XTy并用此方程对 ω \omega ω进行更新计算。Ridge回归的参数估计图为:

椭圆形区域为回归参数的求解空间,蓝色部分为L2正则化约束条件。
LASSO回归和Ridge回归的NumPy手撕代码
LASSO回归的python实现
为了能够使LASSO回归中L1损失的梯度处理,采用一个符号函数来代替1-范数,从而达到能够使LASSO回归的损失函数能够用梯度下降寻优的目的。具体的符号函数如下: sign ( x ) { 1 , x > 0 0 , x = 0 − 1 , x < 0 \operatorname{sign}(x)\left\{\begin{array}{l} 1, x>0 \\ 0, x=0 \\ -1, x<0 \end{array}\right. sign(x)⎩⎨⎧1,x>00,x=0−1,x<0
#定义符号函数
def sign(x):
if x > 0:
return 1
elif x < 0:
return -1
else:
return 0
#对符号函数进行向量化
vec_sign = np.vectorize(sign)
LASSO回归模型主体:
# 定义lasso损失函数
def l1_loss(X, y, w, b, alpha):
num_train = X.shape[0]
num_feature = X.shape[1]
y_hat = np.dot(X, w) + b
loss = np.sum((y_hat-y)**2)/num_train + np.sum(alpha*abs(w))
dw = np.dot(X.T, (y_hat-y)) /num_train + alpha * vec_sign(w)
db = np.sum((y_hat-y)) /num_train
return y_hat, loss, dw, db
其中,α为正则化系数。
Ridge回归的python实现
相较于L1正则化而言,L2正则化则可以直接进行梯度计算。
# 定义ridge损失函数
def l2_loss(X, y, w, b, alpha):
num_train = X.shape[0]
num_feature = X.shape[1]
y_hat = np.dot(X, w) + b
loss = np.sum((y_hat-y)**2)/num_train + alpha*(np.sum(np.square(w)))
dw = np.dot(X.T, (y_hat-y)) /num_train + 2*alpha*w
db = np.sum((y_hat-y)) /num_train
return y_hat, loss, dw, db
训练过程
# 定义参数初始化函数
def initialize(dims):
w = np.zeros((dims, 1))
b = 0
return w, b
# 定义训练过程
def train(X, y, learning_rate=0.01, epochs=300):
loss_list = []
w, b = initialize(X.shape[1])
for i in range(1, epochs):
y_hat, loss, dw, db = l1_loss(X, y, w, b, 0.1) # l2_loss(X, y, w, b, 0.1)
w += -learning_rate * dw
b += -learning_rate * db
loss_list.append(loss)
if i % 300 == 0:
print('epoch %d loss %f' % (i, loss))
params = {
'w': w,
'b': b
}
grads = {
'dw': dw,
'db': db
}
return loss, loss_list, params, grads
#载入数据集
import numpy as np
import pandas as pd
data = np.genfromtxt('example.dat', delimiter = ',')
# 选择特征与标签
x = data[:,0:100]
y = data[:,100].reshape(-1,1)
# 加一列
X = np.column_stack((np.ones((x.shape[0],1)),x))
# 划分训练集与测试集
X_train, y_train = X[:70], y[:70]
X_test, y_test = X[70:], y[70:]
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)
(70, 101) (70, 1) (31, 101) (31, 1)
训练集有70个样本,但特征有101个,属于典型的特征数大于样本量,适用于LASSO回归和Ridge回归模型。
# 执行训练示例
loss, loss_list, params, grads = train(X_train, y_train, 0.01, 3000) # LASSO回归采用train中的l1_loss,Ridge回归采用train中的l2_loss
print(params)
预测过程
# 定义预测函数
def predict(X, params):
w = params['w']
b = params['b']
y_pred = np.dot(X, w) + b
return y_pred
y_pred = predict(X_test, params)