人工智能系列实验（五）——正则化方法：L2正则化和dropout的Python实现

为了解决神经网络过拟合问题，相较于添加数据量的难度于开销，正则化应是我们的首选方法。本实验利用Python，分别实现了L2正则化和dropout两种方法。

L2正则化

L2正则化是解决过拟合的常用方法之一。
实现L2正则化需要两步，分别是1.改变成本函数和2.改变反向传播时偏导数的计算。
1. 在成本函数后加L2尾巴
$$J_{regularized}=\underset{cross-entropycost}{-\frac{1}{m}\sum _{i=1}^m(y^{(i)}log(a^{[L](i)})+(1-y^{(i)})log(1-a^{[L](i)}))}+\underset{L2尾巴}{\frac{1}{m}\frac{\lambda }{2}\sum _l\sum _k\sum _j{W}_{k,j}^{[l]2}}$$
实现代码如下：

# 3层网络
# 获得常规的成本
cross_entropy_cost = compute_cost(A3, Y) 
    
#计算L2尾巴
L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)
        
cost = cross_entropy_cost + L2_regularization_cost

2. 在反向传播计算偏导数时在dW后加上L2尾巴$\frac{\lambda }{m}W$
实现代码如下：

dZ3 = A3 - Y
    
dW3 = 1. / m * np.dot(dZ3, A2.T) + (lambd * W3) / m
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)

dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T) + (lambd * W2) / m
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)

dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T) + (lambd * W1) / m
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)

dropout

dropout也是一个被深度学习领域经常用到的解决过拟合的方法。
dropout在训练的每个回合中都随机地删除一些神经元，每个回合训练的神经网络模型都被改变了。这就避免了对某个样本某个特征过于依赖，以偏概全。从而避免了过拟合的情况。

带dropout的前向传播

1. 使用 np.random.rand()创建一个与$A^{[1]}$维度相同的矩阵$D^{[1]}$。
2. 通过设置阈值的方式来将$D^{[1]}$中(1-keep_prob)百分比个元素设置为0，将占比keep_prob个元素设置为1。
3. 让$A^{[1]}$等于$A^{[1]}\ast D^{[1]}$，这样$A^{[1]}$某些元素与$D^{[1]}$中的0元素相乘之后，$A^{[1]}$中的相应元素也变成0了。相应的a被设置为0后，它对应的神经元就等于被删除掉了。
4. 最后一步，将$A^{[1]}$除以 keep_prob。通过这一步使运用了dropout的神经网络的期望值和没有用dropout的神经网络的期望值保持一样，即实现inverted dropout。

实现代码如下：

Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)

D1 = np.random.rand(A1.shape[0], A1.shape[1])     # 第一步
D1 = D1 < keep_prob                            # 第二步
A1 = A1 * D1                                      # 第三步
A1 = A1 / keep_prob                               # 第四步

Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)

D2 = np.random.rand(A2.shape[0], A2.shape[1])     
D2 = D2 < keep_prob                                             
A2 = A2 * D2                                  
A2 = A2 / keep_prob               

Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)

带dropout的反向传播

1. 在前向传播时，我们通过使用掩码$D^{[1]}$与$A^{[1]}$进行运算而删除了一些神经元。在反向传播时，我们也必须删除相同的神经元，这个可以通过使用相同的$D^{[1]}$与$d{A}^{[1]}$进行运算来实现。
2. 在前向传播时，我们将$A^{[1]}$除以了keep_prob。在反向传播时，我们也必须将$d{A}^{[1]}$除以keep_prob。微积分层面的解释是：如果$A^{[1]}$被keep_prob进行了缩放，那么它的导数$d{A}^{[1]}$也应该被相应地缩放。

实现代码如下：

dZ3 = A3 - Y
dW3 = 1. / m * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)

dA2 = dA2 * D2              # 第一步
dA2 = dA2 / keep_prob              # 第二步

dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)

dA1 = np.dot(W2.T, dZ2)

dA1 = dA1 * D1              
dA1 = dA1 / keep_prob             

dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)

提示

1. dropout是一种正则化技术。
2. 只能在训练模型时运行dropout，在使用模型时要把dropout关掉。
3. 在前向传播和反向传播中都要实现dropout。
4. 在每层的前向传播和反向传播中都除以keep_prob来保证期望值不变。

实际模型效果演示

利用坐标-颜色的数据点集，我们分别用L2正则化和dropout训练预测，与不使用正则化方法的模型进行对比。
关于本实验完整代码详见：
https://github.com/PPPerry/AI_projects/tree/main/5.regularization
未加正则化的模型，对训练数据产生了过拟合：

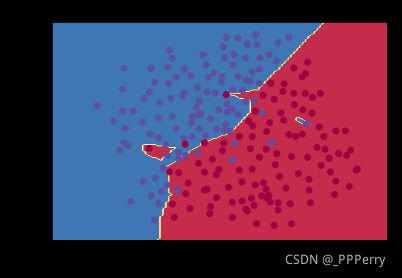
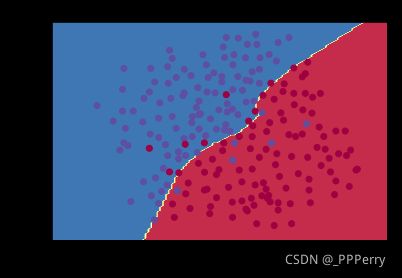
带L2正则化或dropout的模型，对训练数据集不再拟合过度：

往期人工智能系列实验：

人工智能系列实验（一）——用于识别猫的二分类单层神经网络
人工智能系列实验（二）——用于区分不同颜色区域的浅层神经网络
人工智能系列实验（三）——用于识别猫的二分类深度神经网络
人工智能系列实验（四）——多种神经网络参数初始化方法对比（Xavier初始化和He初始化）