深度学习入门

---

序

此文章为深度学习入门的学习内容

---

1、什么是深度学习

1.1 人工智能、机器学习和深度学习

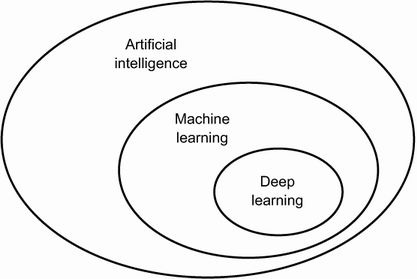
首先，当我们提到人工智能时，我们需要明确定义我们在谈论什么。什么是人工智能、机器学习和深度学习（见图 1.1）？它们之间有什么关系？

图 1.1 人工智能、机器学习和深度学习

1.1.1 人工智能

简而言之，人工智能可以被描述为将通常由人类执行的智力任务自动化的努力。因此，人工智能是一个涵盖机器学习和深度学习的通用领域，但也包括更多可能不涉及任何学习的方法。

事实上，在相当长的一段时间内，大多数专家都认为，通过让程序员手工制定一组足够大的显式规则来操纵存储在显式数据库中的知识，可以实现人类水平的人工智能。这种方法被称为符号 AI。它是从 1950 年代到 1980 年代后期人工智能的主导范式，并在专家系统繁荣时期达到了顶峰80年代。

尽管符号 AI 被证明适合解决定义明确的逻辑问题，例如下棋，但事实证明它很难找出明确的规则来解决更复杂、模糊的问题，例如图像分类、语音识别或自然语言翻译. 一种取代符号 AI 的新方法应运而生：机器学习。

1.1.2 机器学习

让计算机完成有用工作的通常方法是让人类程序员编写遵循规则——一种计算机程序——将输入数据转化为适当的答案，就像洛夫莱斯夫人写下分步说明供分析引擎执行一样。机器学习扭转了这一局面：机器查看输入数据和相应的答案，并找出规则应该是什么（见图 1.2）。训练机器学习系统而不是明确编程。它提供了许多与任务相关的示例，并在这些示例中找到统计结构，最终允许系统提出自动执行任务的规则。

图 1.2 机器学习：一种新的编程范式

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YnV71xVA-1671980336289)(https://drek4537l1klr.cloudfront.net/chollet2/HighResolutionFigures/figure_1-2.png)]

尽管机器学习在 1990 年代才开始蓬勃发展，但它已迅速成为 AI 中最受欢迎和最成功的子领域，这一趋势是由更快的硬件和更大的数据集的可用性推动的。机器学习与数理统计相关，但它在几个重要方面不同于统计，就像医学与化学相关但不能简化为化学一样，因为医学处理的是具有其独特属性的独特系统。与统计学不同，机器学习倾向于处理大型、复杂的数据集（例如包含数百万张图像的数据集，每张图像由数万个像素组成），而经典的统计分析（例如贝叶斯分析）是不切实际的。因此，机器学习，尤其是深度学习，它展示了相对较少的数学理论——也许太少了——并且从根本上说它是一门工程学科。与理论物理学或数学不同，机器学习是一个非常注重实践的领域，由实证发现驱动，并且高度依赖于软件和硬件的进步。

1.1.3 从数据中学习规则和表示

要定义深度学习并了解深度学习与其他机器学习方法之间的区别，首先我们需要了解机器学习算法的作用。我们刚刚说过，机器学习发现了执行数据处理任务的规则，给出了预期的例子。所以，要进行机器学习，我们需要三样东西：

• 输入数据点——例如，如果任务是语音识别，这些数据点可能是人们说话的声音文件。如果任务是图像标记，它们可以是图片。
• 预期输出示例——在语音识别任务中，这些可能是人类生成的声音文件的转录本。在图像任务中，预期输出可能是“狗”、“猫”等标签。
• 一种衡量算法是否做得很好的方法——这是确定算法当前输出与其预期输出之间的距离所必需的。测量结果用作反馈信号以调整算法的工作方式。这个调整步骤就是我们呼唤学习。

机器学习模型将其输入数据转换为有意义的输出，这是一个通过接触已知输入和输出示例“学习”的过程。因此，机器学习和深度学习的核心问题是有意义地转换数据：在其他方面换句话说，学习手头输入数据的有用表示——使我们更接近预期输出的表示。

在我们继续之前：什么是表示？从本质上讲，它是一种查看数据的不同方式——表示或编码数据。例如，彩色图像可以编码为 RGB格式（红-绿-蓝）或 HSV格式（色调-饱和度-值）：这是同一数据的两种不同表示形式。一些用一种表示可能很困难的任务用另一种表示可能会变得容易。例如，任务“选择图像中的所有红色像素”在 RGB 格式中更简单，而“使图像不那么饱和”在 HSV 格式中更简单。机器学习模型都是关于为其输入数据寻找合适的表示形式——数据的转换，使其更适合手头的任务。

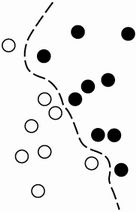
让我们把这个具体化。考虑一个x轴、一个y轴和一些由它们在 ( x , y ) 系统中的坐标表示的点，如图 1.3 所示。

图 1.3 一些示例数据

如您所见，我们有一些白点和一些黑点。假设我们要开发一种算法，可以获取点的坐标 ( x , y ) 并输出该点可能是黑色还是白色。在这种情况下，

• 输入是我们点的坐标。
• 预期输出是我们点的颜色。
• 衡量我们的算法是否做得好的一种方法可以是，例如，被正确分类的点的百分比。

我们在这里需要的是一种新的数据表示方式，可以将白点与黑点完全分开。在许多其他可能性中，我们可以使用的一种变换是坐标变化，如图 1.4 所示。

图 1.4 坐标变化

在这个新的坐标系中，我们点的坐标可以说是我们数据的新表示。这是一个很好的！通过这种表示，黑白分类问题可以表示为一个简单的规则：“黑点是x > 0”或“白点是x < 0”。这种新的表示，结合这个简单的规则，巧妙地解决了分类问题。

在这种情况下，我们手动定义了坐标变化：我们使用人类智能来提出我们自己的适当数据表示。这对于这样一个极其简单的问题来说很好，但是如果任务是对手写数字的图像进行分类，你能做同样的事情吗？你能写下明确的、计算机可执行的图像转换，以阐明 6 和 8 之间、1 和 7 之间以及各种不同手写体之间的区别吗？

这在一定程度上是可能的。基于数字表示的规则，例如“闭环数”或垂直和水平像素直方图，可以很好地区分手写数字。但是，手动找到这样有用的表示是一项艰巨的工作，而且正如您可以想象的那样，由此产生的基于规则的系统很脆弱——维护起来简直就是一场噩梦。每次遇到打破您深思熟虑的规则的新手写示例时，您都必须添加新的数据转换和新规则，同时考虑它们与每个先前规则的交互。

您可能在想，如果这个过程如此痛苦，我们可以将其自动化吗？如果我们尝试系统地搜索不同的自动生成的数据表示集和基于它们的规则，通过使用某些开发数据集中正确分类的数字百分比作为反馈来识别好的表示，会怎样？然后我们将进行机器学习。在机器学习的上下文中，学习描述了一种自动搜索数据转换的过程，该过程在一些反馈信号的指导下产生一些数据的有用表示——这些表示适用于解决手头任务的更简单的规则。

这些变换可以是坐标变化（如在我们的二维坐标分类示例中），或采用像素直方图和计数循环（如在我们的数字分类示例中），但它们也可以是线性投影、平移、非线性操作（如“选择所有满足x > 0” 的点），依此类推。机器学习算法在寻找这些转换时通常没有创造性；他们只是在搜索一组预定义的操作，称为假设空间。例如，空间所有可能的坐标变化的集合将是我们在二维坐标分类示例中的假设空间。

因此，简而言之，这就是机器学习：使用来自反馈信号的指导，在预定义的可能性空间内搜索一些输入数据的有用表示和规则。这个简单的想法可以解决范围非常广泛的智力任务，从语音识别到自动驾驶。

现在您已经理解了我们所说的学习的含义，让我们来看看是什么让深度学习与众不同。

1.1.4 “深度学习”中的“深度”

深度学习是机器学习的一个特定子领域：一种从数据中学习表示的新方法，强调学习越来越有意义的表示的连续层。“深度学习”中的“深度”并不是指通过该方法获得的任何更深入的理解；相反，它代表了连续表示层的想法。有多少层对数据模型有贡献称为模型的深度。该字段的其他适当名称可能有分层表示学习或分层表示学习。现代深学习通常涉及数十甚至数百个连续的表示层，并且它们都是通过接触训练数据自动学习的。同时，其他机器学习方法往往只关注学习一层或两层数据表示（例如，获取像素直方图，然后应用分类规则）; 因此，它们有时被称为浅层学习。

在深度学习中，这些分层表示是通过称为神经网络的模型学习的，其结构为文字层相互堆叠。“神经网络”一词指的是神经生物学，但尽管深度学习中的一些核心概念部分是从我们对大脑（特别是视觉皮层）的理解中汲取灵感而发展起来的，但深度学习模型并不是神经网络的模型。脑。没有证据表明大脑会执行任何类似于现代深度学习模型中使用的学习机制。您可能会看到一些科普文章宣称深度学习像大脑一样工作或以大脑为模型，但事实并非如此。对于该领域的新手来说，如果认为深度学习与神经生物学有任何关系，那将是令人困惑和适得其反的；你不需要那种“就像我们的思想一样”的神秘和神秘的裹尸布，你也可能会忘记你可能读过的关于深度学习和生物学之间假设联系的任何内容。就我们的目的而言，深度学习是一种从数据中学习表征的数学框架。

深度学习算法学习到的表征是什么样的？让我们检查一个多层深度的网络（见图 1.5）如何转换数字图像以识别它是什么数字。

图 1.5 用于数字分类的深度神经网络

正如你在图 1.6 中看到的，网络将数字图像转换成与原始图像越来越不同的表示，并且对最终结果的信息越来越多。您可以将深度网络视为一个多阶段的信息蒸馏过程，其中信息通过连续的过滤器并越来越纯净（即对某些任务有用）。

图 1.6 数字分类模型学习的数据表示

所以从技术上讲，这就是深度学习：一种学习数据表示的多阶段方法。这是一个简单的想法——但事实证明，非常简单的机制，足够大，最终看起来就像魔术一样。

1.1.5 理解深度学习的工作原理，三幅图

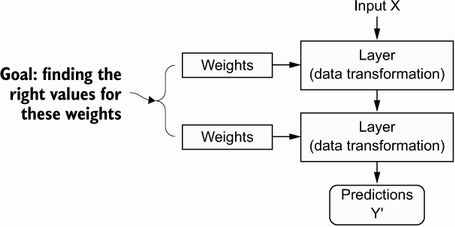
此时，您知道机器学习是关于将输入（例如图像）映射到目标（例如标签“猫”），这是通过观察输入和目标的许多示例来完成的。您还知道，深度神经网络通过简单数据转换（层）的深度序列来完成这种输入到目标的映射，并且这些数据转换是通过接触示例来学习的。现在让我们具体地看看这种学习是如何发生的。

层对其输入数据执行的操作的规范存储在层的权重中，其中本质是一堆数字。用技术术语来说，我们会说层实现的转换由其权重参数化（见图 1.7）。（权重有时也称为层的参数。）在这种情况下，学习意味着为网络中所有层的权重找到一组值，以便网络将示例输入正确映射到它们的相关目标。但问题是：深度神经网络可以包含数千万个参数。为所有参数找到正确的值似乎是一项艰巨的任务，尤其是考虑到修改一个参数的值会影响所有其他参数的行为！

图 1.7 神经网络由其权重参数化。

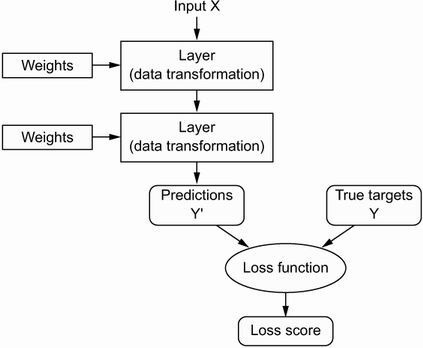
要控制某物，首先你需要能够观察到它。要控制神经网络的输出，您需要能够测量此输出与您的预期相差多远。这是损失函数的工作网络，有时也称为目标函数或成本函数。亏损函数采用网络的预测和真实目标（你希望网络输出什么）并计算距离分数，捕捉网络在这个特定示例上的表现（见图 1.8）。

图 1.8 损失函数衡量网络输出的质量。

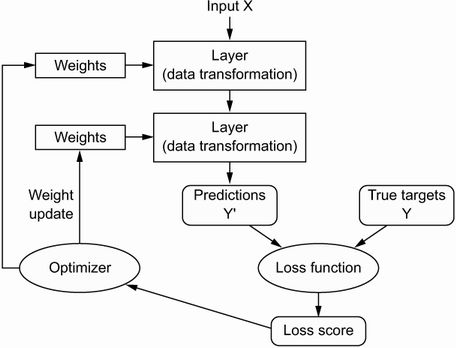
深度学习的基本技巧是使用这个分数作为反馈信号来稍微调整权重值，以降低当前示例的损失分数（见图 1.9）。这种调整是优化器，它实现了所谓的反向传播算法：中央深度学习中的算法。下一章将更详细地解释反向传播的工作原理。

图 1.9 损失分数作为调整权重的反馈信号。

最初，网络的权重被赋予随机值，因此网络仅实现一系列随机变换。自然，它的输出与理想状态相去甚远，损失分数也相应很高。但是对于网络处理的每个示例，权重都会在正确的方向上稍微调整一下，并且损失分数会降低。这是训练循环，重复足够次数（通常在数千个示例中进行数十次迭代），产生最小化损失函数的权重值。具有最小损失的网络是输出尽可能接近目标的网络：训练有素的网络。再一次，这是一个简单的机制，一旦扩展，最终看起来就像魔术一样。

1.2 机器学习简史

深度学习已经达到了人工智能历史上前所未有的公众关注度和行业投资水平，但这并不是机器学习的第一个成功形式。可以肯定地说，当今行业中使用的大多数机器学习算法都不是深度学习算法。深度学习并不总是适合这项工作的工具——有时没有足够的数据让深度学习适用，有时问题可以用不同的算法更好地解决。如果深度学习是你第一次接触机器学习，你可能会发现自己手头只有深度学习锤子，每一个机器学习问题开始看起来都像钉子。不落入这个陷阱的唯一方法是熟悉其他方法并在适当的时候进行实践。

对经典机器学习方法的详细讨论超出了本书的范围，但我将简要介绍它们并描述它们发展的历史背景。这将使我们能够将深度学习置于更广泛的机器学习背景下，并更好地理解深度学习的来源及其重要性。

1.2.1 概率建模

概率建模是统计学原理在数据分析中的应用。它是最早的机器学习形式之一，至今仍在广泛使用。此类别中最著名的算法之一是朴素贝叶斯算法。

朴素贝叶斯是一种基于应用贝叶斯定理的机器学习分类器，同时假设输入数据中的特征都是独立的（强假设或“朴素”假设，这就是名称的由来）。这种形式的数据分析早于计算机，并且在其第一次计算机实施之前几十年就已经被手工应用（很可能可以追溯到 1950 年代）。贝叶斯定理和统计基础可以追溯到 18 世纪，而这些正是您开始使用朴素贝叶斯分类器所需要的。

密切相关的模型是逻辑回归（简称logreg），有时被认为是现代机器学习的“Hello World”。不要被它的名字误导——logreg 是一种分类算法而不是回归算法。与朴素贝叶斯非常相似，logreg 早于计算很长一段时间，但由于其简单和通用的特性，它至今仍然有用。这通常是数据科学家在数据集上尝试的第一件事，以了解手头的分类任务。

1.2.2 早期神经网络

神经网络的早期迭代已完全被这些页面中涵盖的现代变体所取代，但了解深度学习的起源是有帮助的。尽管早在 1950 年代就以玩具形式研究了神经网络的核心思想，但该方法花了数十年时间才开始。长期以来，缺失的部分是训练大型神经网络的有效方法。这种情况在 20 世纪 80 年代中期发生了变化，当时多个人独立地重新发现了反向传播算法——一种使用梯度下降优化来训练参数操作链的方法（我们将在本书后面精确定义这些概念）——并开始将其应用于神经网络网络。

神经网络的第一个成功的实际应用是 1989 年来自贝尔实验室的，当时 Yann LeCun 将卷积神经网络和反向传播的早期思想结合起来，并将其应用于手写数字分类问题。由此产生的网络，称为LeNet，被用于由美国邮政服务于 1990 年代自动读取邮件信封上的邮政编码。

1.2.3 内核方法

随着神经网络在 1990 年代开始在研究人员中获得一些尊重，由于第一次成功，一种新的机器学习方法声名鹊起，并迅速使神经网络被遗忘：内核方法。核方法是一组分类算法，其中最著名的是支持向量机(SVM)。

SVM 是一种分类算法，它通过寻找分隔两个类的“决策边界”来工作（图 1.10）。SVM 继续分两步找到这些边界：

1. 数据被映射到一个新的高维表示，其中决策边界可以表示为超平面（如果数据是二维的，如图 1.10 所示，超平面将是一条直线）。
2. 一个好的决策边界（一个分离超平面）是通过尝试最大化超平面和每个类中最近的数据点之间的距离来计算的，这个步骤称为最大化边距。这允许很好地推广到训练数据集之外的新样本的边界。

图 1.10 决策边界

将数据映射到分类问题变得更简单的高维表示的技术在纸面上看起来不错，但在实践中，它通常在计算上难以处理。这就是内核技巧的用武之地（关键内核方法以其命名的想法）。这是它的要点：要在新的表示空间中找到好的决策超平面，您不必显式计算新空间中点的坐标；您只需要计算该空间中点对之间的距离，这可以使用核函数有效地完成。核函数是计算上易于处理的操作，将初始空间中的任意两点映射到目标表示空间中这些点之间的距离，完全绕过新表示的显式计算。核函数通常是手工制作的，而不是从数据中学习的——在 SVM 的情况下，只学习分离超平面。

在开发时，SVM 在简单分类问题上表现出最先进的性能，并且是为数不多的得到广泛理论支持并经得起严格数学分析的机器学习方法之一，使其易于理解和解释。由于这些有用的特性，支持向量机在很长一段时间内在该领域变得非常流行。

但事实证明，SVM 很难扩展到大型数据集，并且无法为图像分类等感知问题提供良好的结果。由于 SVM 是一种浅层方法，将 SVM 应用于感知问题需要首先手动提取有用的表示（称为特征工程的步骤），这是困难且脆弱的。例如，如果你想使用 SVM 对手写数字进行分类，你不能从原始像素开始；您应该首先手动找到使问题更容易处理的有用表示，例如我之前提到的像素直方图。

1.2.4 决策树、随机森林和梯度提升机

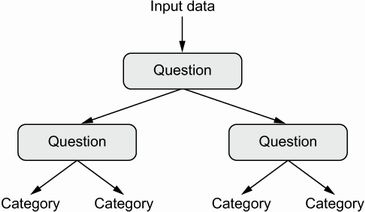
决策树是类似流程图的结构，可让您对输入数据点进行分类或预测给定输入的输出值（见图 1.11）。它们很容易形象化和解释。从数据中学习的决策树在 2000 年代开始受到广泛的研究兴趣，到 2010 年它们通常比核方法更受青睐。

图 1.11 决策树：学习的参数是关于数据的问题。例如，问题可以是“数据中的系数 2 是否大于 3.5？”

特别是，随机森林算法引入了一种稳健、实用的决策树学习方法，涉及构建大量专门的决策树，然后集成它们的输出。随机森林适用于广泛的问题——你可以说它们几乎总是任何浅层机器学习任务的第二好的算法。当流行的机器学习竞赛网站 Kaggle ( http://kaggle.com ) 于 2010 年启动时，随机森林迅速成为该平台上的宠儿——直到 2014 年，梯度提升机器接管了比赛。梯度提升机，很像随机森林，是一种基于集成弱预测模型（通常是决策树）的机器学习技术。它用梯度提升，一种通过迭代训练专门解决先前模型弱点的新模型来改进任何机器学习模型的方法。应用于决策树时，梯度提升技术的使用导致模型在大多数情况下严格优于随机森林，同时具有相似的属性。它可能是当今处理非感知数据*的最佳算法之一，如果不是最佳的话。*除了深度学习，它是 Kaggle 竞赛中最常用的技术之一。

1.2.5 是什么让深度学习与众不同

深度学习如此迅速发展的主要原因是它为许多问题提供了更好的性能。但这不是唯一的原因。深度学习还使解决问题变得更加容易，因为它完全自动化了过去机器学习工作流程中最关键的步骤：特征工程。

以前的机器学习技术——浅层学习——只涉及将输入数据转换成一个或两个连续的表示空间，通常通过简单的转换，如高维非线性投影 (SVM) 或决策树。但复杂问题所需的精细表示通常无法通过此类技术获得。因此，人类不得不竭尽全力使初始输入数据更适合通过这些方法进行处理：他们必须手动为数据设计良好的表示层。这是称为特征工程。另一方面，深度学习完全自动化了此步骤：通过深度学习，您可以一次学习所有功能，而不必自己设计它们。这大大简化了机器学习工作流程，通常用单一、简单、端到端的深度学习模型取代复杂的多级管道。

你可能会问，如果问题的关键是有多个连续的表示层，是否可以重复应用浅层方法来模拟深度学习的效果？在实践中，浅层学习方法的连续应用会产生快速递减的回报，因为三层模型中的最佳第一表示层不是单层或双层模型中的最佳第一层。深度学习的变革性在于它允许模型同时学习所有表示层*，*而不是接连学习（贪婪地，因为它被称为）。通过联合特征学习，每当模型调整其内部特征之一时，依赖它的所有其他特征都会自动适应变化，而无需人工干预。一切都由一个反馈信号监督：模型中的每一个变化都服务于最终目标。这比贪婪地堆叠浅层模型要强大得多，因为它允许通过将复杂的抽象表示分解为长系列的中间空间（层）来学习它们；每个空间都只是与前一个空间的简单转换。

这些是深度学习如何从数据中学习的两个基本特征：渐进的、逐层的方式来开发越来越复杂的表示，以及**这些中间增量表示是联合学习的事实，每一层都被更新以遵循两者上层的代表性需求和下层的需求。这两个属性共同使深度学习比以前的机器学习方法更加成功。

2、神经网络的数学基础

2.1 初识神经网络

我们来看一个具体的神经网络示例，使用 Python 的 Keras 库来学习手写数字分类。我们这里要解决的问题是，将手写数字的灰度图像（28 像素×28 像素）划分到 10 个类别 中（0~9）。这个数据集包含 60 000 张训练图像和 10 000 张测试图像。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xxaSiSN4-1671980336300)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225124650176.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gsbshAzb-1671980336300)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225124701028.png)]

（1）数据集导入

train_images 和 train_labels 组成了训练集（training set），模型将从这些数据中进行 学习。然后在测试集（test set，即 test_images 和 test_labels）上对模型进行测试。 图像被编码为 Numpy 数组，而标签是数字数组，取值范围为 0~9。图像和标签一一对应。

from keras.datasets import mnist

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images.shape
# (60000, 28, 28)

test_images.shape
# (10000, 28, 28)

train_labels.shape
# (60000,)

train_labels
# array([5, 0, 4, ..., 5, 6, 8], dtype=uint8)

接下来的工作流程如下：首先，将训练数据（train_images 和 train_labels）输入神 经网络；其次，网络学习将图像和标签关联在一起；最后，网络对 test_images 生成预测， 而我们将验证这些预测与 test_labels 中的标签是否匹配。

（2）构建网络模型。

from keras import models
from keras import layers

network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))

神经网络的核心组件是层（layer），它是一种数据处理模块，你可以将它看成数据过滤器。 进去一些数据，出来的数据变得更加有用。具体来说，层从输入数据中提取表示——我们期望 这种表示有助于解决手头的问题。大多数深度学习都是将简单的层链接起来，从而实现渐进式 的数据蒸馏（data distillation）。深度学习模型就像是数据处理的筛子，包含一系列越来越精细的 数据过滤器（即层）。 本例中的网络包含 2 个 Dense 层，它们是密集连接（也叫全连接）的神经层。第二层（也 是最后一层）是一个 10 路 softmax 层，它将返回一个由 10 个概率值（总和为 1）组成的数组。 每个概率值表示当前数字图像属于 10 个数字类别中某一个的概率。

（3）编译设置

要想训练网络，我们还需要选择编译（compile）步骤的三个参数。

• 损失函数（loss function）：网络如何衡量在训练数据上的性能，即网络如何朝着正确的 方向前进。
• 优化器（optimizer）：基于训练数据和损失函数来更新网络的机制。
• 在训练和测试过程中需要监控的指标（metric）：本例只关心精度，即正确分类的图像所 占的比例。

network.compile(optimizer='rmsprop',
				loss='categorical_crossentropy',
                metrics=['accuracy'])

（4）数据预处理

在开始训练之前，我们将对数据进行预处理，将其变换为网络要求的形状，并缩放到所 有值都在 [0, 1] 区间。比如，之前训练图像保存在一个 uint8 类型的数组中，其形状为 (60000, 28, 28)，取值区间为 [0, 255]。我们需要将其变换为一个 float32 数组，其形 状为 (60000, 28 * 28)，取值范围为 0~1。

train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

我们还需要对标签进行分类编码。这一步是将一个个的label转化为向量的形式（one-hot encoding）。

from keras.utils import to_categorical
train_labels = to_categorical(train_labels) #2 -> (0,0,1,0,0,0,0,0,0,0)表示原标签为0-9中的2.
test_labels = to_categorical(test_labels)

原始标签的类型为：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6BDYMrqA-1671980336301)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225130012174.png)]

转换之后的类型为：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ki4MTvmX-1671980336301)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225130142051.png)]

（5）模型训练

现在我们准备开始训练网络，在 Keras 中这一步是通过调用网络的 fit 方法来完成的—— 我们在训练数据上拟合（fit）模型。

network.fit(train_images, train_labels, epochs=5, batch_size=128)
# Epoch 1/5
# 469/469 [==============================] - 11s 2ms/step - loss: 0.4350 - accuracy: 0.8738
# Epoch 2/5
# 469/469 [==============================] - 1s 1ms/step - loss: 0.1107 - accuracy: 0.9674
# Epoch 3/5
# 469/469 [==============================] - 1s 1ms/step - loss: 0.0686 - accuracy: 0.9796
# Epoch 4/5
# 469/469 [==============================] - 1s 2ms/step - loss: 0.0509 - accuracy: 0.9848
# Epoch 5/5
# 469/469 [==============================] - 1s 2ms/step - loss: 0.0349 - accuracy: 0.9898

训练过程中显示了两个数字：一个是网络在训练数据上的损失（loss），另一个是网络在 训练数据上的精度（acc）。 我们很快就在训练数据上达到了 0.989（98.9%）的精度。现在我们来检查一下模型在测试 集上的性能。

（6）模型测试

test_loss, test_acc = network.evaluate(test_images, test_labels)
# 313/313 [==============================] - 1s 2ms/step - loss: 0.0626 - accuracy: 0.9809

训练精度和测试精度之间的这种差距是过拟 合（overfit）造成的。过拟合是指机器学习模型在新数据上的性能往往比在训练数据上要差。

第一个例子到这里就结束了。你刚刚看到了如何构建和训练一个神经网络，用不到 20 行的 Python 代码对手写数字进行分类。下一章会详细介绍这个例子中的每一个步骤，并讲解其背后 的原理。接下来你将要学到张量（输入网络的数据存储对象）、张量运算（层的组成要素）和梯 度下降（可以让网络从训练样本中进行学习）。

2.2 神经网络的数据表示

前面例子使用的数据存储在多维 Numpy 数组中，也叫张量（tensor）。一般来说，当前所有机器学习系统都使用张量作为基本数据结构。那么什么是张量？ 张量这一概念的核心在于，它是一个数据容器。它包含的数据几乎总是数值数据，因此它是数字的容器。你可能对矩阵很熟悉，它是二维张量。张量是矩阵向任意维度的推广［注意， 张量的维度（dimension）通常叫作轴（axis）］。

2.2.1 标量（0D 张量）

仅包含一个数字的张量叫作标量（scalar，也叫标量张量、零维张量、0D 张量）。在 Numpy 中，一个 float32 或 float64 的数字就是一个标量张量（或标量数组）。你可以用 ndim 属性来查看一个 Numpy 张量的轴的个数。标量张量有 0 个轴（ndim == 0）。张量轴的个数也叫作阶（rank）。下面是一个 Numpy 标量。

import numpy as np
x = np.array(12)
x	# array(12)
x.ndim	# 0

2.2.2 向量（1D 张量）

数字组成的数组叫作向量（vector）或一维张量（1D 张量）。一维张量只有一个轴。下面是 一个 Numpy 向量。

import numpy as np
x = np.array([12, 3, 6, 14, 7])
x	# array([12,  3,  6, 14,  7])
x.ndim	# 1

2.2.3 矩阵（2D张量）

向量组成的数组叫作矩阵（matrix）或二维张量（2D 张量）。矩阵有 2 个轴（通常叫作行和 列）。你可以将矩阵直观地理解为数字组成的矩形网格。下面是一个 Numpy 矩阵。

x = np.array([[5, 78, 2, 34, 0],
             [6, 79, 3, 35, 1],
             [7, 80, 4, 36, 2]])
x.ndim	# 2

第一个轴上的元素叫作行（row），第二个轴上的元素叫作列（column）。在上面的例子中， [5, 78, 2, 34, 0] 是 x 的第一行，[5, 6, 7] 是第一列。

2.2.4 3D 张量与更高维张量

将多个矩阵组合成一个新的数组，可以得到一个 3D 张量，你可以将其直观地理解为数字 组成的立方体。下面是一个 Numpy 的 3D 张量。

x = np.array([[[5, 78, 2, 34, 0],
               [6, 79, 3, 35, 1],
               [7, 80, 4, 36, 2]],
              
               [[5, 78, 2, 34, 0],
               [6, 79, 3, 35, 1],
               [7, 80, 4, 36, 2]],
               
               [[5, 78, 2, 34, 0],
               [6, 79, 3, 35, 1],
               [7, 80, 4, 36, 2]]])
x.ndim # 3

将多个 3D 张量组合成一个数组，可以创建一个 4D 张量，以此类推。深度学习处理的一般 是 0D 到 4D 的张量，但处理视频数据时可能会遇到 5D 张量。

2.2.5 关键属性

张量是由以下三个关键属性来定义的。

• 轴的个数（阶）。例如，3D 张量有 3 个轴，矩阵有 2 个轴。这在 Numpy 等 Python 库中 也叫张量的 ndim。
• 形状。这是一个整数元组，表示张量沿每个轴的维度大小（元素个数）。例如，前面矩 阵示例的形状为 (3, 5)，3D 张量示例的形状为 (3, 3, 5)。向量的形状只包含一个 元素，比如 (5,)，而标量的形状为空，即 ()。
• 数据类型（在 Python 库中通常叫作 dtype）。这是张量中所包含数据的类型，例如，张量的类型可以是 float32、uint8、float64 等。在极少数情况下，你可能会遇到字符 （char）张量。

注意，Numpy（以及大多数其他库）中不存在字符串张量，因为张量存 储在预先分配的连续内存段中，而字符串的长度是可变的，无法用这种方式存储。

为了具体说明，我们回头看一下 MNIST 例子中处理的数据。

train_images.shape	# (60000, 28, 28)
train_images.ndim	# 3
(train_images.dtype # uint8

所以，这里 train_images 是一个由 8 位整数组成的 3D 张量。更确切地说，它是 60000个矩阵组成的数组，每个矩阵由 28×28 个整数组成。每个这样的矩阵都是一张灰度图像，元素取值范围为 0~255。

我们用 Matplotlib 库（Python 标准科学套件的一部分）来显示这个 3D 张量中的第 4 个数字， 如图 2-2 所示。

digit = train_images[4]
import matplotlib.pyplot as plt
plt.imshow(digit, cmap=plt.cm.binary)
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VZ6YHZlK-1671980336301)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225132021507.png)]

2.2.6 在Numpy中操作张量

在前面的例子中，我们使用语法 train_images[i] 来选择沿着第一个轴的特定数字。选 择张量的特定元素叫作张量切片（tensor slicing）。我们来看一下 Numpy 数组上的张量切片运算。 下面这个例子选择第 10~100 个数字（不包括第 100 个），并将其放在形状为 (90, 28, 28) 的数组中。

my_slice = train_images[10:100]

print(my_slice.shape) # (90, 28, 28)

它等同于下面这个更复杂的写法，给出了切片沿着每个张量轴的起始索引和结束索引。 注意，: 等同于选择整个轴。

my_slice = train_images[10:100, :, :] 

my_slice.shape # (90, 28, 28) 

my_slice = train_images[10:100, 0:28, 0:28]

my_slice.shape # (90, 28, 28)

一般来说，你可以沿着每个张量轴在任意两个索引之间进行选择。例如，你可以在所有图 像的右下角选出 14 像素×14 像素的区域：

my_slice = train_images[:, 14:, 14:] 

也可以使用负数索引。与 Python 列表中的负数索引类似，它表示与当前轴终点的相对位置。 你可以在图像中心裁剪出 14 像素×14 像素的区域：

 my_slice = train_images[:, 7:-7, 7:-7]

2.2.7 数据批量的概念

通常来说，深度学习中所有数据张量的第一个轴（0 轴，因为索引从 0 开始）都是样本轴 （samples axis，有时也叫样本维度）。在 MNIST 的例子中，样本就是数字图像。 此外，深度学习模型不会同时处理整个数据集，而是将数据拆分成小批量。具体来看，下 面是 MNIST 数据集的一个批量batch，批量大小batch_size为 128。

batch = train_images[:128] 
len(batch)	# 128

然后是下一个批量。

batch = train_images[128:256] 

然后是第 n 个批量。

 batch = train_images[128 * n:128 * (n + 1)] 

对于这种批量张量，第一个轴（0 轴）叫作批量轴（batch axis）或批量维度（batch dimension）。 在使用 Keras 和其他深度学习库时，你会经常遇到这个术语。

2.2.8 现实世界中的数据张量

我们用几个你未来会遇到的示例来具体介绍数据张量。你需要处理的数据几乎总是以下类 别之一。

• 向量数据：2D 张量，形状为 (samples, features)。 features也可以是多维向量。MLP / Dense
• 时间序列数据或序列数据：3D 张量，形状为 (samples, timesteps, features)。 RNN
• 图像：4D 张量，形状为 (samples, height, width, channels) 或 (samples, channels, height, width)。 CNN
• 视频：5D 张量，形状为 (samples, frames, height, width, channels) 或 (samples, frames, channels, height, width)。

2.2.9 向量数据

这是最常见的数据。对于这种数据集，每个数据点都被编码为一个向量，因此一个数据批 量就被编码为 2D 张量（即向量组成的数组），其中第一个轴是样本轴，第二个轴是特征轴。

我们来看两个例子。

人口统计数据集，其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值 的向量，而整个数据集包含 100 000 个人，因此可以存储在形状为 (100000, 3) 的 2D 张量中。

文本文档数据集，我们将每个文档表示为每个单词在其中出现的次数（字典中包含 20000 个常见单词）。每个文档可以被编码为包含 20000 个值的向量（每个值对应于字典中每个单词的出现次数），整个数据集包含 500 个文档，因此可以存储在形状为 (500, 20000) 的张量中。

2.2.10 时间序列数据或序列数据

当时间（或序列顺序）对于数据很重要时，应该将数据存储在带有时间轴的 3D 张量中。 每个样本可以被编码为一个向量序列（即 2D 张量，时间步数 + 各采样点的特征），因此一个数据批量就被编码为一个 3D 张 量（见图 2-3）。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DsNBagrb-1671980336302)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225142551567.png)]

根据惯例，时间轴始终是第 2 个轴（索引为 1 的轴）。我们来看几个例子。

• 股票价格数据集。每一分钟，我们将股票的当前价格、前一分钟的最高价格和前一分钟 的最低价格保存下来。因此每分钟被编码为一个 3D 向量，整个交易日被编码为一个形 状为 (390, 3) 的 2D 张量（一个交易日有 390 分钟），而 250 天的数据则可以保存在一 个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据。
• 推文数据集。我们将每条推文编码为 280 个字符组成的序列，而每个字符又来自于 128 个字符组成的字母表。在这种情况下，每个字符可以被编码为大小为 128 的二进制向量 （只有在该字符对应的索引位置取值为 1，其他元素都为 0）。那么每条推文可以被编码 为一个形状为 (280, 128) 的 2D 张量，而包含 100 万条推文的数据集则可以存储在一 个形状为 (1000000, 280, 128) 的张量中。一个字符是128维向量，一个文章一个280个字符，一个数据集一共1000000篇文章。（samples, timesteps, features）

2.2.11 图像数据

图像通常具有三个维度：高度、宽度和颜色深度。虽然灰度图像（比如 MNIST 数字图像） 只有一个颜色通道，因此可以保存在 2D 张量中，但按照惯例，图像张量始终都是 3D 张量，灰 度图像的彩色通道只有一维。因此，如果图像大小为 256×256，那么 128 张灰度图像组成的批 量可以保存在一个形状为 (128, 256, 256, 1) 的张量中，而 128 张彩色图像组成的批量则可以保存在一个形状为 (128, 256, 256, 3) 的张量中（见图 2-4）。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vUYeg3W4-1671980336302)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225142902554.png)]

图像张量的形状有两种约定：通道在后（channels-last）的约定（在 TensorFlow 中使用）和通道在前（channels-first）的约定（在 Theano 中使用）。Google 的 TensorFlow 机器学习框架将颜色深度轴放在最后：(samples, height, width, color_depth)。与此相反，Theano 将图像深度轴放在批量轴之后：(samples, color_depth, height, width)。如果采用 Theano 约定，前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256)。 Keras 框架同时支持这两种格式。单色的图由[height, width]组成，RGB则为[3, height, width]。

2.2.12 视频数据

视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。视频可以看作一系列帧， 每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_ depth) 的 3D 张量中，因此一系列帧可以保存在一个形状为 (frames, height, width, color_depth) 的 4D 张量中，而不同视频组成的批量则可以保存在一个 5D 张量中，其形状为 (samples, frames, height, width, color_depth)。 举个例子，一个以每秒 4 帧采样的 60 秒 YouTube 视频片段，视频尺寸为 144×256，这个 视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3) 的张量中。总共有 106 168 320 个值！如果张量的数据类型（dtype）是 float32，每个值都是 32 位，那么这个张量共有 405MB。好大！你在现实生活中遇到的视频要小得多，因为它们不以 float32 格式存储，而且通常被大大压缩，比如 MPEG 格式。

2.3 神经网络的“齿轮”：张量运算

所有计算机程序最终都可以简化为二进制输入上的一些二进制运算（AND、OR、NOR 等）， 与此类似，深度神经网络学到的所有变换也都可以简化为数值数据张量上的一些张量运算（tensor operation），例如加上张量、乘以张量等。 在最开始的例子中，我们通过叠加 Dense 层来构建网络。Keras 层的实例如下所示。

keras.layers.Dense(512, activation='relu')

这个层可以理解为一个函数，输入一个 2D 张量，返回另一个 2D 张量，即输入张量的新 表示。具体而言，这个函数如下所示（其中 W 是一个 2D 张量，b 是一个向量，二者都是该层的 属性）。

output = relu(dot(W, input) + b)

我们将上式拆开来看。这里有三个张量运算：输入张量和张量 W 之间的点积运算（dot）、 得到的 2D 张量与向量 b 之间的加法运算（+）、最后的 relu 运算。relu(x) 是 max(x, 0)。

2.3.1 逐元素运算

relu 运算和加法都是逐元素（element-wise）的运算，即该运算独立地应用于张量中的每个元素，也就是说，这些运算非常适合大规模并行实现（向量化实现，所以其实每次输入的不是一个样本，而是一个batchsize维的样本，同时进行计算。其次，每个向量中的值都会同时计算）。下列代码是对逐元素 relu 运算的简单实现。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uGo05dtb-1671980336302)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225143530383.png)]

在实践中处理 Numpy 数组时，这些运算都是优化好的 Numpy 内置函数，这些函数将大量运算交给安装好的基础线性代数子程序（BLAS，basic linear algebra subprograms）实现（没装的话，应该装一个）。BLAS 是低层次的、高度并行的、高效的张量操作程序，通常用 Fortran 或 C 语言来实现。

因此，在 Numpy 中可以直接进行下列逐元素运算，速度非常快。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Fl1gYloZ-1671980336302)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225143703294.png)]

2.3.2 广播

上一节 naive_add 的简单实现仅支持两个形状相同的 2D 张量相加。但在前面介绍的 Dense 层中，我们将一个 2D 张量与一个向量相加。如果将两个形状不同的张量相加，会发生 什么？ 如果没有歧义的话，较小的张量会被广播（broadcast），以匹配较大张量的形状。广播包含 以下两步。 (1) 向较小的张量添加轴（叫作广播轴），使其 ndim 与较大的张量相同。 (2) 将较小的张量沿着新轴重复，使其形状与较大的张量相同。 来看一个具体的例子。假设 X 的形状是 (32, 10)，y 的形状是 (10,)。首先，我们给 y 添加空的第一个轴，这样 y 的形状变为 (1, 10)。然后，我们将 y 沿着新轴重复 32 次，这样 得到的张量 Y 的形状为 (32, 10)，并且 Y[i, :] == y for i in range(0, 32)。现在， 我们可以将 X 和 Y 相加，因为它们的形状相同。 在实际的实现过程中并不会创建新的 2D 张量，因为那样做非常低效。重复的操作完全是 虚拟的，它只出现在算法中，而没有发生在内存中。但想象将向量沿着新轴重复 10 次，是一种 很有用的思维模型。下面是一种简单的实现。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l0oh0YBQ-1671980336302)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225145150684.png)]

如果一个张量的形状是 (a, b, … n, n+1, … m)，另一个张量的形状是 (n, n+1, … m)，那么你通常可以利用广播对它们做两个张量之间的逐元素运算。广播操作会自动应用 于从 a 到 n-1 的轴。 下面这个例子利用广播将逐元素的 maximum 运算应用于两个形状不同的张量。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-irHkBFw6-1671980336303)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225145159549.png)]

2.3.3 张量点积

点积运算，也叫张量积（tensor product，不要与逐元素的乘积弄混），是最常见也最有用的 张量运算。与逐元素的运算不同，它将输入张量的元素合并在一起。 在 Numpy、Keras、Theano 和 TensorFlow 中，都是用 * 实现逐元素乘积。TensorFlow 中的 点积使用了不同的语法，但在 Numpy 和 Keras 中，都是用标准的 dot 运算符来实现点积。z = np.dot(x, y)

注意，两个向量之间的点积是一个标量，而且只有元素个数相同的向量之间才能做点积。 你还可以对一个矩阵 x 和一个向量 y 做点积，返回值是一个向量，其中每个元素是 y 和 x 的每一行之间的点积。

为了便于理解点积的形状匹配，可以将输入张量和输出张量像图 2-5 中那样排列，利用可 视化来帮助理解。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6naeKfR4-1671980336303)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225145415581.png)]

图 2-5 中，x、y 和 z 都用矩形表示（元素按矩形排列）。x 的行和 y 的列必须大小相同，因 此 x 的宽度一定等于 y 的高度。如果你打算开发新的机器学习算法，可能经常要画这种图。 更一般地说，你可以对更高维的张量做点积，只要其形状匹配遵循与前面 2D 张量相同的原则：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4KHv0j29-1671980336303)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225145454466.png)]

2.3.4 张量变形

第三个重要的张量运算是张量变形（tensor reshaping）。虽然前面神经网络第一个例子的 Dense 层中没有用到它，但在将图像数据输入神经网络之前，我们在预处理时用到了这个运算。

train_images = train_images.reshape((60000, 28 * 28))

张量变形是指改变张量的行和列，以得到想要的形状。变形后的张量的元素总个数与初始 张量相同。简单的例子可以帮助我们理解张量变形。

x = np.array([[0., 1.],
             [2., 3.],
             [4., 5.]])
print(x.shape) #(3, 2)

x = x.reshape((6, 1))
x #array([[ 0.],
  #       [ 1.],
  #       [ 2.],
  #       [ 3.],
  #       [ 4.],
  #       [ 5.]])
         
x = x.reshape((2, 3))
x #array([[ 0., 1., 2.],
  #		 [ 3., 4., 5.]])

经常遇到的一种特殊的张量变形是转置transposition)。对矩阵做转置是指将行和列互换， 使 x[i, :] 变为 x[:, i]。

x = np.zeros((300, 20)) #创建一个形状为 (300, 20) 的零矩阵
x = np.transpose(x)
print(x.shape) #(20, 300)

2.3.5 深度学习的几何解释

神经网络完全由一系列张量运算组成，而这些张量运算都只是输入数据的几何 变换。因此，你可以将神经网络解释为高维空间中非常复杂的几何变换，这种变换可以通过许 多简单的步骤来实现。 对于三维的情况，下面这个思维图像是很有用的。想象有两张彩纸：一张红色，一张蓝色。将其中一张纸放在另一张上。现在将两张纸一起揉成小球。这个皱巴巴的纸球就是你的输入数 据，每张纸对应于分类问题中的一个类别。神经网络（或者任何机器学习模型）要做的就是找 到可以让纸球恢复平整的变换，从而能够再次让两个类别明确可分。通过深度学习，这一过程 可以用三维空间中一系列简单的变换来实现，比如你用手指对纸球做的变换，每次做一个动作， 如图 2-9 所示。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9lq3Cbuo-1671980336303)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225152307847.png)]

让纸球恢复平整就是机器学习的内容：为复杂的、高度折叠的数据流形找到简洁的表示。 现在你应该能够很好地理解，为什么深度学习特别擅长这一点：它将复杂的几何变换逐步分解 为一长串基本的几何变换，这与人类展开纸球所采取的策略大致相同。深度网络的每一层都通 过变换使数据解开一点点——许多层堆叠在一起，可以实现非常复杂的解开过程。

2.4 神经网络的“引擎”：基于梯度的优化

上一节介绍过，我们的第一个神经网络示例中，每个神经层都用下述方法对输入数据进行 变换。

output = relu(dot(W, input) + b)

在这个表达式中，W 和 b 都是张量，均为该层的属性。它们被称为该层的权重（weight）或 可训练参数（trainable parameter），分别对应 kernel 和 bias 属性。这些权重包含网络从观察 训练数据中学到的信息。

一开始，这些权重矩阵取较小的随机值，这一步叫作随机初始化（random initialization）。 当然，W 和 b 都是随机的，relu(dot(W, input) + b) 肯定不会得到任何有用的表示。虽然 得到的表示是没有意义的，但这是一个起点。下一步则是根据反馈信号逐渐调节这些权重。这 个逐渐调节的过程叫作训练，也就是机器学习中的学习。

上述过程发生在一个训练循环（training loop）内，其具体过程如下。必要时一直重复这些步骤。

1. 抽取训练样本 x 和对应目标 y 组成的数据批量。
2. 在 x 上运行网络［这一步叫作前向传播 (forward pass)］，得到预测值 y_pred。
3. 计算网络在这批数据上的损失，用于衡量 y_pred 和 y 之间的距离。
4. 更新网络的所有权重，使网络在这批数据上的损失略微下降。

最终得到的网络在训练数据上的损失非常小，即预测值 y_pred 和预期目标 y 之间的距离 非常小。网络“学会”将输入映射到正确的目标。乍一看可能像魔法一样，但如果你将其简化为基本步骤，那么会变得非常简单。

第一步看起来非常简单，只是输入 / 输出（I/O）的代码。

第二步和第三步仅仅是一些张量运算的应用，所以你完全可以利用上一节学到的知识来实现这两步。

难点在于第四步：更新网络的权重。考虑网络中某个权重系数，你怎么知道这个系数应该增大还是减小，以及变化多少？

一种简单的解决方案是，保持网络中其他权重不变，只考虑某个标量系数，让其尝试不同的取值。假设这个系数的初始值为 0.3。对一批数据做完前向传播后，网络在这批数据上的损失是 0.5。如果你将这个系数的值改为 0.35 并重新运行前向传播，损失会增大到 0.6。但如果你将 这个系数减小到 0.25，损失会减小到 0.4。在这个例子中，将这个系数减小 0.05 似乎有助于使 损失最小化。对于网络中的所有系数都要重复这一过程。 但这种方法是非常低效的，因为对每个系数（系数很多，通常有上千个，有时甚至多达上 百万个）都需要计算两次前向传播（计算代价很大）。

一种更好的方法是利用网络中所有运算都是可微（differentiable）的这一事实，计算损失相对于网络系数的梯度（gradient），然后向梯度 的反方向改变系数，从而使损失降低。

2.4.1 张量运算的导数：梯度

梯度（gradient）是张量运算的导数。它是导数这一概念向多元函数导数的推广。多元函数 是以张量作为输入的函数。

假设有一个输入向量 x、一个矩阵 W、一个目标 y 和一个损失函数 loss。你可以用 W 来计 算预测值 y_pred，然后计算损失，或者说预测值 y_pred 和目标 y 之间的距离。

 y_pred = dot(W, x) 
 loss_value = loss(y_pred, y) 

如果输入数据 x 和 y 保持不变，那么这可以看作将 W 映射到损失值的函数。

loss_value = f(W) 

假设 W 的当前值为 W0。f 在 W0 点的导数是一个张量 gradient(f)(W0)，其形状与 W 相同， 每个系数 gradient(f)(W0)[i, j] 表示改变 W0[i, j] 时 loss_value 变化的方向和大小。 张量 gradient(f)(W0) 是函数 f(W) = loss_value 在 W0 的导数。

前面已经看到，单变量函数 f(x) 的导数可以看作函数 f 曲线的斜率。同样，gradient(f) (W0) 也可以看作表示 f(W) 在 W0 附近曲率（curvature）的张量。

对于一个函数 f(x)，你可以通过将 x 向导数的反方向移动一小步来减小 f(x) 的值。同样，对于张量的函数 f(W)，你也可以通过将 W 向梯度的反方向移动来减小 f(W)，比如 W1 = W0 - step * gradient(f)(W0)，其中 step 是一个很小的比例因子。也就是说，沿着曲 率的反方向移动，直观上来看在曲线上的位置会更低。注意，比例因子 step 是必需的，因为 gradient(f)(W0) 只是 W0 附近曲率的近似值，不能离 W0 太远。

2.4.2 随机梯度下降

给定一个可微函数，理论上可以用解析法找到它的最小值：函数的最小值是导数为 0 的点， 因此你只需找到所有导数为 0 的点，然后计算函数在其中哪个点具有最小值。

将这一方法应用于神经网络，就是用解析法求出最小损失函数对应的所有权重值。可以通 过对方程 gradient(f)(W) = 0 求解 W 来实现这一方法。这是包含 N 个变量的多项式方程， 其中 N 是网络中系数的个数。N=2 或 N=3 时可以对这样的方程求解，但对于实际的神经网络是 无法求解的，因为参数的个数不会少于几千个，而且经常有上千万个。

相反，你可以使用 2.4 节开头总结的四步算法：基于当前在随机数据批量上的损失，一点一点地对参数进行调节。由于处理的是一个可微函数，你可以计算出它的梯度，从而有效地实 现第四步。沿着梯度的反方向更新权重，损失每次都会变小一点。

1. 抽取训练样本 x 和对应目标 y 组成的数据批量。
2. 在 x 上运行网络，得到预测值 y_pred。
3. 计算网络在这批数据上的损失，用于衡量 y_pred 和 y 之间的距离。
4. 计算损失相对于网络参数的梯度［一次反向传播（backward pass）］。
5. 将参数沿着梯度的反方向移动一点，比如 W -= step * gradient，从而使这批数据上的损失减小一点。

这很简单！我刚刚描述的方法叫作小批量随机梯度下降（mini-batch stochastic gradient descent， 又称为小批量 SGD）。术语随机（stochastic）是指每批数据都是随机抽取的（stochastic 是 random 在科学上的同义词 a）。图 2-11 给出了一维的情况，网络只有一个参数，并且只有一个训练样本。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LnZaGVjY-1671980336304)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225153619838.png)]

如你所见，直观上来看，为 step 因子选取合适的值是很重要的。如果取值太小，则沿着 曲线的下降需要很多次迭代，而且可能会陷入局部极小点。如果取值太大，则更新权重值之后 可能会出现在曲线上完全随机的位置。

注意，小批量 SGD 算法的一个变体是每次迭代时只抽取一个样本和目标，而不是抽取一批 数据。这叫作真 SGD（有别于小批量 SGD）。还有另一种极端，每一次迭代都在所有数据上 运行，这叫作批量 SGD。这样做的话，每次更新都更加准确，但计算代价也高得多。这两个极 端之间的有效折中则是选择合理的批量大小。

此外，SGD 还有多种变体，其区别在于计算下一次权重更新时还要考虑上一次权重更新， 而不是仅仅考虑当前梯度值，比如带动量的 SGD、Adagrad、RMSProp 等变体。这些变体被称 为优化方法（optimization method）或优化器（optimizer）。其中动量的概念尤其值得关注，它在 许多变体中都有应用。动量解决了 SGD 的两个问题：收敛速度和局部极小点。图 2-13 给出了 损失作为网络参数的函数的曲线。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2eXLRFMO-1671980336304)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225153752369.png)]

如你所见，在某个参数值附近，有一个局部极小点（local minimum）：在这个点附近，向 左移动和向右移动都会导致损失值增大。如果使用小学习率的 SGD 进行优化，那么优化过程可 能会陷入局部极小点，导致无法找到全局最小点。 使用动量方法可以避免这样的问题，这一方法的灵感来源于物理学。有一种有用的思维图像， 就是将优化过程想象成一个小球从损失函数曲线上滚下来。如果小球的动量足够大，那么它不会 卡在峡谷里，最终会到达全局最小点。动量方法的实现过程是每一步都移动小球，不仅要考虑当 前的斜率值（当前的加速度），还要考虑当前的速度（来自于之前的加速度）。这在实践中的是指， 更新参数 w 不仅要考虑当前的梯度值，还要考虑上一次的参数更新，其简单实现如下所示。

past_velocity = 0.
momentum = 0.1		# 不变的动量因子
while loss > 0.01:	# 优化循环
    w, loss, gradient = get_current_parameters()
    velocity = past_velocity * momentum - learning_rate * gradient
    w = w + momentum * velocity - learning_rate * gradient
    past_velocity = velocity
    update_parameter(w)

2.4.3 链式求导：反向传播算法

在前面的算法中，我们假设函数是可微的，因此可以明确计算其导数。在实践中，神经网 络函数包含许多连接在一起的张量运算，每个运算都有简单的、已知的导数。

例如，下面这个 网络 f 包含 3 个张量运算 a、b 和 c，还有 3 个权重矩阵 W1、W2 和 W3。

f(W1, W2, W3) = a(W1, b(W2, c(W3))) 

根据微积分的知识，这种函数链可以利用下面这个恒等式进行求导，它称为链式法则（chain rule）：(f(g(x)))’ = f’(g(x)) * g’(x)。将链式法则应用于神经网络梯度值的计算，得 到的算法叫作反向传播（backpropagation，有时也叫反式微分，reverse-mode differentiation）。反向传播从最终损失值开始，从最顶层反向作用至最底层，利用链式法则计算每个参数对损失值 的贡献大小。

现在以及未来数年，人们将使用能够进行符号微分（symbolic differentiation）的现代框架来实现神经网络，比如 TensorFlow。也就是说，给定一个运算链，并且已知每个运算的导数，这些框架就可以利用链式法则来计算这个运算链的梯度函数，将网络参数值映射为梯度值。对于 这样的函数，反向传播就简化为调用这个梯度函数。由于符号微分的出现，你无须手动实现反向传播算法。因此，我们不会在本节浪费你的时间和精力来推导反向传播的具体公式。你只需充分理解基于梯度的优化方法的工作原理。

2.4.4 回顾MNIST

我们回头 看一下第一个例子，并根据前面三节学到的内容来重新阅读这个例子中的每一段代码。

下面是输入数据。

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

现在你明白了，输入图像保存在 float32 格式的 Numpy 张量中，形状分别为 (60000, 784)（训练数据）和 (10000, 784)（测试数据）。

下面是构建网络。

network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))

现在你明白了，这个网络包含两个 Dense 层，每层都对输入数据进行一些简单的张量运算， 这些运算都包含权重张量。权重张量是该层的属性，里面保存了网络所学到的知识（knowledge）。

下面是模型的编译。

network.compile(optimizer='rmsprop',
                loss='categorical_crossentropy',
                metrics=['accuracy'])

现在你明白了，categorical_crossentropy 是损失函数，是用于学习权重张量的反馈 信号，在训练阶段应使它最小化。你还知道，减小损失是通过小批量随机梯度下降来实现的。 梯度下降的具体方法由第一个参数给定，即 rmsprop 优化器。

最后，下面是训练循环。

network.fit(train_images, train_labels, epochs=5, batch_size=128)

现在你明白在调用 fit 时发生了什么：网络开始在训练数据上进行迭代（每个小批量包含 128 个样本），共迭代 5 次［在所有训练数据上迭代一次叫作一个轮次（epoch）］。在每次迭代过程中，网络会计算批量损失相对于权重的梯度，并相应地更新权重。5 轮之后，网络进行了 2345 次梯度更新（每轮 469 次），网络损失值将变得足够小，使得网络能够以很高的精度对手 写数字进行分类。

2.5 本章小结

• 学习是指找到一组模型参数，使得在给定的训练数据样本和对应目标值上的损失函数最小化。
• 学习的过程：随机选取包含数据样本及其目标值的批量，并计算批量损失相对于网络参数的梯度。随后将网络参数沿着梯度的反方向稍稍移动（移动距离由学习率指定）。
• 整个学习过程之所以能够实现，是因为神经网络是一系列可微分的张量运算，因此可以利用求导的链式法则来得到梯度函数，这个函数将当前参数和当前数据批量映射为一个 梯度值。
• 后续几章你会经常遇到两个关键的概念：损失和优化器。将数据输入网络之前，你需要先定义这二者。
• 损失是在训练过程中需要最小化的量，因此，它应该能够衡量当前任务是否已成功解决。
• 优化器是使用损失梯度更新参数的具体方式，比如 RMSProp 优化器、带动量的随机梯 度下降（SGD）等。

3、神经网络入门

本章将进一步介绍神经网络的核心组件，即层、网络、目标函数和优化器；还会简要介绍 Keras，它是贯穿本书的 Python 深度学习库。最后，我们将用三个介绍性示例深入讲解如何使用神经网络解决实际问题， 这三个示例分别是：

• 将电影评论划分为正面或负面（二分类问题）
• 将新闻按主题分类（多分类问题）
• 根据房地产数据估算房屋价格（回归问题）

学完本章，你将能够使用神经网络解决简单的机器问题，比如对向量数据的分类问题和回归问题。然后，你就可以从第 4 章开始建立对机器学习更加具有原则性、理论性的理解。

3.1 神经网络剖析

前面几章介绍过，训练神经网络主要围绕以下四个方面。

• 层，多个层组合成网络（或模型）。
• 输入数据和相应的目标。
• 损失函数，即用于学习的反馈信号。
• 优化器，决定学习过程如何进行。

你可以将这四者的关系可视化，如图 3-1 所示：多个层链接在一起组成了网络，将输入数 据映射为预测值。然后损失函数将这些预测值与目标进行比较，得到损失值，用于衡量网络预 测值与预期结果的匹配程度。优化器使用这个损失值来更新网络的权重。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iMDaIUu1-1671980336304)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225154823363.png)]

3.1.1 层：深度学习的基础组件

神经网络的基本数据结构是层。层是一个数据处理模块，将一个 或多个输入张量转换为一个或多个输出张量。有些层是无状态的，但大多数的层是有状态的， 即层的权重。权重是利用随机梯度下降学到的一个或多个张量，其中包含网络的知识。

不同的张量格式与不同的数据处理类型需要用到不同的层。例如，

• 简单的向量数据保存在形状为 (samples, features) 的 2D 张量中，通常用全连接层（FC）或密集层（dense layer），对应于 Keras 的 Dense 类］来处理。
• 序列数据保存在形状为 (samples, timesteps, features) 的 3D 张量中，通常用循环层（recurrent layer，比如 Keras 的 LSTM 层）来处理。
• 图像数据保存在 4D 张量中，通常用二维 卷积层（Keras 的 Conv2D）来处理。

你可以将层看作深度学习的乐高积木，Keras 等框架则将这种比喻具体化。在 Keras 中，构 建深度学习模型就是将相互兼容的多个层拼接在一起，以建立有用的数据变换流程。这里层兼 容性（layer compatibility）具体指的是每一层只接受特定形状的输入张量，并返回特定形状的输出张量。看看下面这个例子。

from keras import layers
layer = layers.Dense(32, input_shape=(784,))	#有 32 个输出单元的密集层

我们创建了一个层，只接受第一个维度大小为 784 的 2D 张量（第 0 轴是批量维度，其大小没有指定，因此可以任意取值）作为输入。这个层将返回一个张量，第一个维度的大小变成了 32。 因此，这个层后面只能连接一个接受 32 维向量作为输入的层。使用 Keras 时，你无须担心 兼容性，因为向模型中添加的层都会自动匹配输入层的形状，例如下面这段代码。

from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(32, input_shape=(784,)))
model.add(layers.Dense(16))

其中第二层没有输入形状（input_shape）的参数，相反，它可以自动推导出输入形状等 于上一层的输出形状。

3.1.2 模型：层构成的网络

深度学习模型是层构成的有向无环图。最常见的例子就是层的线性堆叠，将单一输入映射 为单一输出。

但随着深入学习，你会接触到更多类型的网络拓扑结构。一些常见的网络拓扑结构如下。

• 双分支（two-branch）网络
• 多头（multihead）网络
• Inception 模块

网络的拓扑结构定义了一个假设空间（hypothesis space）。你可能还记得第 1 章里机器学习 的定义：“在预先定义好的可能性空间中，利用反馈信号的指引来寻找输入数据的有用表示。” 选定了网络拓扑结构，意味着将可能性空间（假设空间）限定为一系列特定的张量运算，将输 入数据映射为输出数据。然后，你需要为这些张量运算的权重张量找到一组合适的值。

选择正确的网络架构更像是一门艺术而不是科学。虽然有一些最佳实践和原则，但只有动手实践才能让你成为合格的神经网络架构师。后面几章将教你构建神经网络的详细原则，也会帮你建立直觉，明白对于特定问题哪些架构有用、哪些架构无用。

3.1.3 损失函数与优化器：配置学习过程的关键

一旦确定了网络架构，你还需要选择以下两个参数。

• 损失函数（目标函数）——在训练过程中需要将其最小化。它能够衡量当前任务是否已 成功完成。
• 优化器——决定如何基于损失函数对网络进行更新。它执行的是随机梯度下降（SGD） 的某个变体。

具有多个输出的神经网络可能具有多个损失函数（每个输出对应一个损失函数）。但是，梯度下降过程必须基于单个标量损失值。因此，对于具有多个损失函数的网络，需要将所有损失函数取平均，变为一个标量值。

选择正确的目标函数对解决问题是非常重要的。网络的目的是使损失尽可能最小化，因此， 如果目标函数与成功完成当前任务不完全相关，那么网络最终得到的结果可能会不符合你的预 期。想象一下，利用 SGD 训练一个愚蠢而又无所不能的人工智能，给它一个蹩脚的目标函数：“将 所有活着的人的平均幸福感最大化”。为了简化自己的工作，这个人工智能可能会选择杀死绝大 多数人类，只留几个人并专注于这几个人的幸福——因为平均幸福感并不受人数的影响。这可 能并不是你想要的结果！请记住，你构建的所有神经网络在降低损失函数时和上述的人工智能 一样无情。因此，一定要明智地选择目标函数，否则你将会遇到意想不到的副作用。

幸运的是，对于分类、回归、序列预测等常见问题，你可以遵循一些简单的指导原则来选 择正确的损失函数。例如，对于二分类问题，你可以使用二元交叉熵（binary crossentropy）损 失函数；对于多分类问题，可以用分类交叉熵（categorical crossentropy）损失函数；对于回归 问题，可以用均方误差（mean-squared error）损失函数；对于序列学习问题，可以用联结主义 时序分类（CTC，connectionist temporal classification）损失函数，等等。只有在面对真正全新的 研究问题时，你才需要自主开发目标函数。在后面几章里，我们将详细说明对于各种常见任务 应选择哪种损失函数。

3.2 Keras 简介

Keras 是一个模型级（model-level）的库，为开发深度学习模型提供了高层次的构建模块。 它不处理张量操作、求微分等低层次的运算。相反，它依赖于一个专门的、高度优化的张量库 来完成这些运算，这个张量库就是 Keras 的后端引擎（backend engine）。Keras 没有选择单个张 量库并将 Keras 实现与这个库绑定，而是以模块化的方式处理这个问题（见图 3-3）。因此，几 个不同的后端引擎都可以无缝嵌入到 Keras 中。目前，Keras 有三个后端实现：TensorFlow 后端、 Theano 后端和微软认知工具包（CNTK，Microsoft cognitive toolkit）后端。未来 Keras 可能会扩 展到支持更多的深度学习引擎。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ykiO6XWw-1671980336304)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225160453268.png)]

我们推荐使用 TensorFlow 后端作为大部分深度学习任务的默认后端，因为它 的应用最广泛，可扩展，而且可用于生产环境。 通过 TensorFlow（或 Theano、CNTK），Keras 可以在 CPU 和 GPU 上无缝运行。在 CPU 上运行 时，TensorFlow 本身封装了一个低层次的张量运算库，叫作 Eigen；在 GPU 上运行时，TensorFlow 封装了一个高度优化的深度学习运算库，叫作 NVIDIA CUDA 深度神经网络库（cuDNN）。

3.2.1 使用Keras开发：概述

你已经见过一个 Keras 模型的示例，就是 MNIST 的例子。典型的 Keras 工作流程就和那个 例子类似。

1. 定义训练数据：输入张量和目标张量。
2. 定义层组成的网络（或模型），将输入映射到目标。
3. 配置学习过程：选择损失函数、优化器和需要监控的指标。
4. 调用模型的 fit 方法在训练数据上进行迭代。

定义模型有两种方法：一种是使用 Sequential 类（仅用于层的线性堆叠，这是目前最常 见的网络架构），另一种是函数式 API（functional API，用于层组成的有向无环图，让你可以构建任意形式的架构）。

前面讲过，这是一个利用 Sequential 类定义的两层模型（注意，我们向第一层传入了输 入数据的预期形状）。

from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(32, activation='relu', input_shape=(784,)))
model.add(layers.Dense(10, activation='softmax'))

下面是用函数式 API 定义的相同模型。

input_tensor = layers.Input(shape=(784,))
x = layers.Dense(32, activation='relu')(input_tensor)
output_tensor = layers.Dense(10, activation='softmax')(x)
model = models.Model(inputs=input_tensor, outputs=output_tensor)

利用函数式 API，你可以操纵模型处理的数据张量，并将层应用于这个张量，就好像这些 层是函数一样。

一旦定义好了模型架构，使用 Sequential 模型还是函数式 API 就不重要了。接下来的步 骤都是相同的。 配置学习过程是在编译这一步，你需要指定模型使用的优化器和损失函数，以及训练过程中想要监控的指标。下面是单一损失函数的例子，这也是目前最常见的。

from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
			loss='mse',
			metrics=['accuracy'])

最后，学习过程就是通过 fit() 方法将输入数据的 Numpy 数组（和对应的目标数据）传 入模型，这一做法与 Scikit-Learn 及其他机器学习库类似。

model.fit(input_tensor, target_tensor, batch_size=128, epochs=10)

3.3 电影评论分类：二分类问题

二分类问题可能是应用最广泛的机器学习问题。在这个例子中，你将学习根据电影评论的 文字内容将其划分为正面或负面。

3.3.1 IMDB 数据集

本节使用 IMDB 数据集，它包含来自互联网电影数据库（IMDB）的 50000 条严重两极分化的评论。数据集被分为用于训练的 25000 条评论与用于测试的 25000 条评论，训练集和测试集都包含 50% 的正面评论和 50% 的负面评论。

为什么要将训练集和测试集分开？因为你不应该将训练机器学习模型的同一批数据再用于测试模型！模型在训练数据上的表现很好，并不意味着它在前所未见的数据上也会表现得很好， 而且你真正关心的是模型在新数据上的性能（因为你已经知道了训练数据对应的标签，显然不再需要模型来进行预测）。例如，你的模型最终可能只是记住了训练样本和目标值之间的映射关系，但这对在前所未见的数据上进行预测毫无用处。下一章将会更详细地讨论这一点。

与 MNIST 数据集一样，IMDB 数据集也内置于 Keras 库。它已经过预处理：评论（单词序列） 已经被转换为整数序列，其中每个整数代表字典中的某个单词。

from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)

参数 num_words=10000 的意思是仅保留训练数据中前10000 个最常出现的单词。低频单词将被舍弃。这样得到的向量数据不会太大，便于处理。

train_data 和 test_data 这两个变量都是评论组成的列表，每条评论又是单词索引组成的列表（表示一系列单词）。train_labels 和 test_labels 都是 0 和 1 组成的列表，其中 0 代表负面（negative），1 代表正面（positive）。

train_data[0]	# [1, 14, ... 178, 32]：一个样本就是一行向量，代表了这一句话的所有出现过的单词。
train_labels[0]	# 1

下面这段代码可以将某条评论迅速解码为英文单词。

word_index = imdb.get_word_index()	# word_index 是一个将单词映射为整数索引的字典
reverse_word_index = dict(
     [(value, key) for (key, value) in word_index.items()]) # 键值颠倒，将整数索引映射为单词
decoded_review = ' '.join(
     [reverse_word_index.get(i - 3, '?') for i in train_data[0]])
# 将评论解码。注意，索引减去了 3，因为 0、1、2是为“padding”（填充）、“start of sequence”（序列开始）、“unknown”（未知词）分别保留的索引

3.3.2 准备数据

你不能将整数序列直接输入神经网络。你需要将列表转换为张量。转换方法有以下两种。

• 填充列表，使其具有相同的长度，再将列表转换成形状为 (samples, word_indices) 的整数张量，然后网络第一层使用能处理这种整数张量的层（即 Embedding 层，本书 后面会详细介绍）。
• 对列表进行 one-hot 编码，将其转换为 0 和 1 组成的向量。举个例子，序列 [3, 5] 将会被转换为 10000 维向量，只有索引为 3 和 5 的元素是 1，其余元素都是 0。然后网络第一层可以用 Dense 层，它能够处理浮点数向量数据。

下面我们采用后一种方法将数据向量化。为了加深理解，你可以手动实现这一方法，如下 所示。

import numpy as np
def vectorize_sequences(sequences, dimension=10000):
    results = np.zeros((len(sequences), dimension)) # 创建一个形状为(len(sequences), dimension) 的零矩阵
    for i, sequence in enumerate(sequences):	
    	results[i, sequence] = 1.	# 将 results[i] 的指定索引设为 1
    return results
x_train = vectorize_sequences(train_data)	# 将训练数据向量化
x_test = vectorize_sequences(test_data)		# 将测试数据向量化

样本现在变成了这样：

x_train[0] array([ 0., 1., 1., ..., 0., 0., 0.]) 

你还应该将标签向量化，这很简单。

y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')

3.3.3 构建模型

输入数据是向量，而标签是标量（1 和 0），这是你会遇到的最简单的情况。有一类网络在这种问题上表现很好，就是带有 relu 激活的全连接层（Dense）的简单堆叠，比如 Dense(16, activation=‘relu’)。

传入 Dense 层的参数（16）是该层隐藏单元的个数。一个隐藏单元（hidden unit）是该层表示空间的一个维度。我们在第 2 章讲过，每个带有 relu 激活的 Dense 层都实现了下列张量运算：

output = relu(dot(W, input) + b)

16 个隐藏单元对应的权重矩阵 W 的形状为 (input_dimension, 16)，与 W 做点积相当于将输入数据投影到 16 维表示空间中（然后再加上偏置向量 b 并应用 relu 运算）。你可以将表示空间的维度直观地理解为“网络学习内部表示时所拥有的自由度”。隐藏单元越多（即更高维的表示空间），网络越能够学到更加复杂的表示，但网络的计算代价也变得更大，而且可能会导致学到不好的模式（这种模式会提高训练数据上的性能，但不会提高测试数据上的性能）。

对于这种 Dense 层的堆叠，你需要确定以下两个关键架构：

• 网络有多少层
• 每层有多少个隐藏单元

第 4 章中的原则将会指导你对上述问题做出选择。现在你只需要相信我选择的下列架构：

• 两个中间层，每层都有 16 个隐藏单元
• 第三层输出一个标量，预测当前评论的情感。

中间层使用 relu 作为激活函数，最后一层使用 sigmoid 激活以输出一个 0~1 范围内的概率值（表示样本的目标值等于 1 的可能性，即评论为正面的可能性）。relu（rectified linear unit， 整流线性单元）函数将所有负值归零（见图 3-4），而 sigmoid 函数则将任意值“压缩”到 [0, 1] 区间内（见图 3-5），其输出值可以看作概率值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gmWvsIQJ-1671980336305)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225170029855.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-krCqn7AG-1671980336305)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225170036444.png)]

图 3-6 显示了网络的结构。代码清单 3-3 是其 Keras 实现，与前面见过的 MNIST 例子类似。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QdfPdKF9-1671980336305)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225170057716.png)]

from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

什么是激活函数？为什么要使用激活函数？

如果没有 relu 等激活函数（也叫非线性），Dense 层将只包含两个线性运算——点积 和加法： output = dot(W, input) + b 这样 Dense 层就只能学习输入数据的线性变换（仿射变换）：该层的假设空间是从输 入数据到 16 位空间所有可能的线性变换集合。这种假设空间非常有限，无法利用多个表示层的优势，因为多个线性层堆叠实现的仍是线性运算，添加层数并不会扩展假设空间。 为了得到更丰富的假设空间，从而充分利用多层表示的优势，你需要添加非线性或激 活函数。relu 是深度学习中最常用的激活函数，但还有许多其他函数可选，它们都有类似 的奇怪名称，比如 prelu、elu 等。

最后，你需要选择损失函数和优化器。

由于你面对的是一个二分类问题，网络输出是一个概率值（网络最后一层使用 sigmoid 激活函数，仅包含一个单元），那么最好使用 binary_ crossentropy（二元交叉熵）损失。这并不是唯一可行的选择，比如你还可以使用 mean_ squared_error（均方误差）。但对于输出概率值的模型，交叉熵（crossentropy）往往是最好 的选择。交叉熵是来自于信息论领域的概念，用于衡量概率分布之间的距离，在这个例子中就是真实分布与预测值之间的距离。

下面的步骤是用 rmsprop 优化器和 binary_crossentropy 损失函数来配置模型。注意，我们还在训练过程中监控精度。

model.compile(optimizer='rmsprop',
			  loss='binary_crossentropy',
			  metrics=['accuracy'])

上述代码将优化器、损失函数和指标作为字符串传入，这是因为 rmsprop、binary_ crossentropy 和 accuracy 都是 Keras 内置的一部分。有时你可能希望配置自定义优化器的 参数，或者传入自定义的损失函数或指标函数。前者可通过向 optimizer 参数传入一个优化器 类实例来实现，如代码清单 3-5 所示；后者可通过向 loss 和 metrics 参数传入函数对象来实现， 如代码清单 3-6 所示。

配置优化器

from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
			  loss='binary_crossentropy',
			  metrics=['accuracy'])

使用自定义的损失和指标

from keras import losses
from keras import metrics
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
			  loss=losses.binary_crossentropy,
			  metrics=[metrics.binary_accuracy])

3.3.4 验证你的方法

为了在训练过程中监控模型在前所未见的数据上的精度，你需要将原始训练数据留出 10000 个样本作为验证集。

留出验证集

x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]

现在使用 512 个样本组成的小批量，将模型训练 20 个轮次（即对 x_train 和 y_train 两 个张量中的所有样本进行 20 次迭代）。与此同时，你还要监控在留出的 10 000 个样本上的损失 和精度。你可以通过将验证数据传入 validation_data 参数来完成。

训练模型

model.compile(optimizer='rmsprop',
			  loss='binary_crossentropy',
			  metrics=['acc'])

history = model.fit(partial_x_train, 
                    partial_y_train,
					epochs=20,
					batch_size=512,
					validation_data=(x_val, y_val))

注意，调用 model.fit() 返回了一个 History 对象。这个对象有一个成员 history，它 是一个字典，包含训练过程中的所有数据。我们来看一下。

history_dict = history.history
history_dict.keys()
dict_keys(['val_acc', 'acc', 'val_loss', 'loss'])

字典中包含 4 个条目，对应训练过程和验证过程中监控的指标。在下面两个代码清单中， 我们将使用 Matplotlib 在同一张图上绘制训练损失和验证损失（见图 3-7），以及训练精度和验 证精度（见图 3-8）。请注意，由于网络的随机初始化不同，你得到的结果可能会略有不同。

绘制训练损失和验证损失

import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')	# 'bo' 表示蓝色圆点
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')	# 'b' 表示蓝色实线
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3Ajw4afC-1671980336305)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225170929015.png)]

绘制训练精度和验证精度

plt.clf()	# 清空图像
acc = history_dict['acc']
val_acc = history_dict['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-09osrRwO-1671980336306)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225171000157.png)]

训练损失每轮都在降低，训练精度每轮都在提升。这就是梯度下降优化的预期 结果——你想要最小化的量随着每次迭代越来越小。但验证损失和验证精度并非如此：它们似乎在第四轮达到最佳值。这就是我们之前警告过的一种情况：模型在训练数据上的表现越来越好， 但在前所未见的数据上不一定表现得越来越好。

准确地说，你看到的是过拟合（overfit）：在第 二轮之后，你对训练数据过度优化，最终学到的表示仅针对于训练数据，无法泛化到训练集之 外的数据。 在这种情况下，为了防止过拟合，你可以在 3 轮之后停止训练。通常来说，你可以使用许多方法来降低过拟合，我们将在第 4 章中详细介绍。

从头开始重新训练一个模型

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
			  loss='binary_crossentropy',
			  metrics=['accuracy'])
model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)

results	# [0.2929924130630493, 0.88327999999999995]

3.3.5 使用训练好的网络在新数据上生成预测结果

训练好网络之后，你希望将其用于实践。你可以用 predict 方法来得到评论为正面的可能性大小。

model.predict(x_test)
'''
array([[ 0.98006207]
      [ 0.99758697]
      [ 0.99975556]
      ...,
      [ 0.82167041]
      [ 0.02885115]
      [ 0.65371346]], dtype=float32)
'''

3.3.6 进一步的实验

通过以下实验，你可以确信前面选择的网络架构是非常合理的，虽然仍有改进的空间。

• 前面使用了两个隐藏层。你可以尝试使用一个或三个隐藏层，然后观察对验证精度和测 试精度的影响。
• 尝试使用更多或更少的隐藏单元，比如 32 个、64 个等。
• 尝试使用 mse 损失函数代替 binary_crossentropy。
• 尝试使用 tanh 激活（这种激活在神经网络早期非常流行）代替 relu。

3.3.7 小结

下面是你应该从这个例子中学到的要点。

• 通常需要对原始数据进行大量预处理，以便将其转换为张量输入到神经网络中。单词序列可以编码为二进制向量，但也有其他编码方式。

• 带有 relu 激活的 Dense 层堆叠，可以解决很多种问题（包括情感分类），你可能会经 常用到这种模型。

• 对于二分类问题（两个输出类别），网络的最后一层应该是只有一个单元并使用 sigmoid 激活的 Dense 层，网络输出应该是 0~1 范围内的标量，表示概率值。

• 对于二分类问题的 sigmoid 标量输出，你应该使用 binary_crossentropy 损失函数。

• 无论你的问题是什么，rmsprop 优化器通常都是足够好的选择。这一点你无须担心。

• 随着神经网络在训练数据上的表现越来越好，模型最终会过拟合，并在前所未见的数据 上得到越来越差的结果。一定要一直监控模型在训练集之外的数据上的性能。

3.4 新闻分类：多分类问题

本节你会构建一个网络，将路透社新闻划分为 46 个互斥的主题。因为有多个类别，所以 这是多分类（multiclass classification）问题的一个例子。因为每个数据点只能划分到一个类别， 所以更具体地说，这是单标签、多分类（single-label, multiclass classification）问题的一个例 子。如果每个数据点可以划分到多个类别（主题），那它就是一个多标签、多分类（multilabel, multiclass classification）问题。

3.4.1 路透社数据集

本节使用路透社数据集，它包含许多短新闻及其对应的主题，由路透社在 1986 年发布。它 是一个简单的、广泛使用的文本分类数据集。它包括 46 个不同的主题：某些主题的样本更多， 但训练集中每个主题都有至少 10 个样本。

加载路透社数据集

from keras.datasets import reuters
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=10000)

与 IMDB 数据集一样，参数 num_words=10000 将数据限定为前 10 000 个最常出现的单词。 我们有 8982 个训练样本和 2246 个测试样本。

与 IMDB 评论一样，每个样本都是一个整数列表（表示单词索引）。

train_data[10]

'''
[1, 245, 273, 207, 156, 53, 74, 160, 26, 14, 46, 296, 26, 39, 74, 2979,
3554, 14, 46, 4689, 4329, 86, 61, 3499, 4795, 14, 61, 451, 4329, 17, 12]
'''

样本对应的标签是一个 0~45 范围内的整数，即话题索引编号。

train_labels[10]	# 3

3.4.2 准备数据

import numpy as np
def vectorize_sequences(sequences, dimension=10000):
    results = np.zeros((len(sequences), dimension))
    for i, sequence in enumerate(sequences):
        results[i, sequence] = 1.
    return results
x_train = vectorize_sequences(train_data)	# 将训练数据向量化
x_test = vectorize_sequences(test_data)		# 将测试数据向量化

将标签向量化有两种方法：你可以将标签列表转换为整数张量，或者使用 one-hot 编码。 one-hot 编码是分类数据广泛使用的一种格式，也叫分类编码（categorical encoding）。6.1 节给出 了 one-hot 编码的详细解释。在这个例子中，标签的 one-hot 编码就是将每个标签表示为全零向量， 只有标签索引对应的元素为 1。其代码实现如下。例如：[0, 0, 1, 0, … , 0]

def to_one_hot(labels, dimension=46):
	results = np.zeros((len(labels), dimension))
    for i, label in enumerate(labels):
    	results[i, label] = 1.
    return results
one_hot_train_labels = to_one_hot(train_labels)
one_hot_test_labels = to_one_hot(test_labels)

注意，Keras 内置方法可以实现这个操作，你在 MNIST 例子中已经见过这种方法。

from keras.utils.np_utils import to_categorical
one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)

3.4.3 构建模型

这个主题分类问题与前面的电影评论分类问题类似，两个例子都是试图对简短的文本片段进行分类。但这个问题有一个新的约束条件：输出类别的数量从 2 个变为 46 个。输出空间的维度要大得多。

对于前面用过的 Dense 层的堆叠，每层只能访问上一层输出的信息。如果某一层丢失了与 分类问题相关的一些信息，那么这些信息无法被后面的层找回，也就是说，每一层都可能成为 信息瓶颈。上一个例子使用了 16 维的中间层，但对这个例子来说 16 维空间可能太小了，无法 学会区分 46 个不同的类别。这种维度较小的层可能成为信息瓶颈，永久地丢失相关信息。

出于这个原因，下面将使用维度更大的层，包含 64 个单元。

模型定义

from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

关于这个架构还应该注意另外两点。

• 网络的最后一层是大小为 46 的 Dense 层。这意味着，对于每个输入样本，网络都会输 出一个 46 维向量。这个向量的每个元素（即每个维度）代表不同的输出类别。
• 最后一层使用了 softmax 激活。你在 MNIST 例子中见过这种用法。网络将输出在 46 个不同输出类别上的概率分布——对于每一个输入样本，网络都会输出一个 46 维向量， 其中 output[i] 是样本属于第 i 个类别的概率。46 个概率的总和为 1。

对于这个例子，最好的损失函数是 categorical_crossentropy（分类交叉熵）。它用于 衡量两个概率分布之间的距离，这里两个概率分布分别是网络输出的概率分布和标签的真实分 布。通过将这两个分布的距离最小化，训练网络可使输出结果尽可能接近真实标签。

编译模型

model.compile(optimizer='rmsprop',
			  loss='categorical_crossentropy',
			  metrics=['accuracy'])

3.4.4 验证你的方法

验证集

x_val = x_train[:1000]
partial_x_train = x_train[1000:]
y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]

训练模型

history = model.fit(partial_x_train,
                    partial_y_train,
                    epochs=20,
                    batch_size=512,
                    validation_data=(x_val, y_val))

绘制曲线

# 训练损失和验证损失
import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-73R35rXg-1671980336306)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225172454672.png)]

# 训练精度和验证精度
plt.clf()	# 清空图像
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lHQGT0VX-1671980336306)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225172533628.png)]

网络在训练 9 轮后开始过拟合。我们从头开始训练一个新网络，共 9 个轮次，然后在测试 集上评估模型。

从头开始重新训练一个模型

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop',
			  loss='categorical_crossentropy',
			  metrics=['accuracy'])
model.fit(partial_x_train,
		  partial_y_train,
		  epochs=9,
		  batch_size=512,
		  validation_data=(x_val, y_val))
results = model.evaluate(x_test, one_hot_test_labels)

# 结果
results	# [0.9565213431445807, 0.79697239536954589]

这种方法可以得到约 80% 的精度。对于平衡的二分类问题，完全随机的分类器能够得到 50% 的精度。但在这个例子中，完全随机的精度约为19%，所以上述结果相当不错，至少和随机的基准比起来还不错。

import copy
test_labels_copy = copy.copy(test_labels)
np.random.shuffle(test_labels_copy)
hits_array = np.array(test_labels) == np.array(test_labels_copy)
float(np.sum(hits_array)) / len(test_labels)	# 0.18655387355298308

3.4.5 使用训练好的网络在新数据上生成预测结果

你可以验证，模型实例的 predict 方法返回了在 46 个主题上的概率分布。我们对所有测 试数据生成主题预测。

predictions = model.predict(x_test)
predictions[0].shape	# (46,)
np.sum(predictions[0])	# 1.0
np.argmax(predictions[0])	# 4 常用于测试

3.4.6 处理标签和损失的另一种方法

前面提到了另一种编码标签的方法，就是将其转换为整数张量，如下所示。

y_train = np.array(train_labels)
y_test = np.array(test_labels)

对于这种编码方法，唯一需要改变的是损失函数的选择。对于分类编码标签使用的损失函数应该使用 categorical_crossentropy。对于整数标签，你应该使用 sparse_categorical_crossentropy。

model.compile(optimizer='rmsprop',
			  loss='sparse_categorical_crossentropy',
			  metrics=['acc'])

这个新的损失函数在数学上与 categorical_crossentropy 完全相同，二者只是接口不同。

3.4.7 中间层维度足够大的重要性

前面提到，最终输出是 46 维的，因此中间层的隐藏单元个数不应该比 46 小太多。现在来 看一下，如果中间层的维度远远小于 46（比如 4 维），造成了信息瓶颈，那么会发生什么？

具有信息瓶颈的模型

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(4, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop',
			  loss='categorical_crossentropy',
			  metrics=['accuracy'])
model.fit(partial_x_train,
          partial_y_train,
          epochs=20,
          batch_size=128,
          validation_data=(x_val, y_val))

现在网络的验证精度最大约为 71%，比前面下降了 8%。导致这一下降的主要原因在于，你 试图将大量信息（这些信息足够恢复 46 个类别的分割超平面）压缩到维度很小的中间空间。网 络能够将大部分必要信息塞入这个四维表示中，但并不是全部信息。

3.4.8 小结

下面是你应该从这个例子中学到的要点。

• 如果要对 N 个类别的数据点进行分类，网络的最后一层应该是大小为 N 的 Dense 层。

• 对于单标签、多分类问题，网络的最后一层应该使用 softmax 激活，这样可以输出在 N 个输出类别上的概率分布。

• 这种问题的损失函数几乎总是应该使用分类交叉熵。它将网络输出的概率分布与目标的 真实分布之间的距离最小化。

• 处理多分类问题的标签有两种方法。

  ​ 通过分类编码（ one-hot 编码）对标签进行编码，然后使用 categorical_ crossentropy 作为损失函数。

  ​ 将标签编码为整数，然后使用 sparse_categorical_crossentropy 损失函数。

• 如果你需要将数据划分到许多类别中，应该避免使用太小的中间层，以免在网络中造成信息瓶颈。

3.5 预测房价：回归问题

前面两个例子都是分类问题，其目标是预测输入数据点所对应的单一离散的标签。另一种 常见的机器学习问题是回归问题，它预测一个连续值而不是离散的标签，例如，根据气象数据 预测明天的气温，或者根据软件说明书预测完成软件项目所需要的时间。

不要将回归问题与 logistic 回归算法混为一谈。令人困惑的是，logistic 回归不是回归算法， 而是分类算法。

3.5.1 波士顿房价数据集

本节将要预测 20 世纪 70 年代中期波士顿郊区房屋价格的中位数，已知当时郊区的一些数据点，比如犯罪率、当地房产税率等。本节用到的数据集与前面两个例子有一个有趣的区别。 它包含的数据点相对较少，只有 506 个，分为 404 个训练样本和 102 个测试样本。输入数据的每个特征（比如犯罪率）都有不同的取值范围。例如，有些特性是比例，取值范围为 0~1；有的取值范围为 1~12；还有的取值范围为 0~100，等等。

加载波士顿房价数据

from keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()

我们来看一下数据。

train_data.shape	# (404, 13)
test_data.shape		# (102, 13)

如你所见，我们有 404 个训练样本和 102 个测试样本，每个样本都有 13 个数值特征，比如人均犯罪率、每个住宅的平均房间数、高速公路可达性等。 目标是房屋价格的中位数，单位是千美元。

train_targets		# array([ 15.2, 42.3, 50. ... 19.4, 19.4, 29.1]) 单位是k dollar

房价大都在10000~50000美元。如果你觉得这很便宜，不要忘记当时是 20 世纪 70 年代中期，而且这些价格没有根据通货膨胀进行调整。

3.5.2 数据归一化

将取值范围差异很大的数据输入到神经网络中，这是有问题的。网络可能会自动适应这种取值范围不同的数据，但学习肯定变得更加困难。对于这种数据，普遍采用的最佳实践是对每个特征做标准化，即对于输入数据的每个特征（输入数据矩阵中的列），减去特征平均值，再除以标准差，这样得到的特征平均值为 0，标准差为 1。用 Numpy 可以很容易实现标准化。

数据标准化

mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std

注意，用于测试数据标准化的均值和标准差都是在训练数据上计算得到的。在工作流程中， 你不能使用在测试数据上计算得到的任何结果，即使是像数据标准化这么简单的事情也不行。

3.5.3 构建模型

由于样本数量很少，我们将使用一个非常小的网络，其中包含两个隐藏层，每层有 64 个单 元。一般来说，训练数据越少，过拟合会越严重，而较小的网络可以降低过拟合。因为需要将同一个模型多次实例化， 所以用一个函数来构建模型。

from keras import models
from keras import layers
def build_model():
    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu',
    input_shape=(train_data.shape[1],)))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
	return model

网络的最后一层只有一个单元，没有激活，是一个线性层。这是标量回归（标量回归是预测单一连续值的回归）的典型设置。添加激活函数将会限制输出范围。例如，如果向最后一层 添加 sigmoid 激活函数，网络只能学会预测 0~1 范围内的值。这里最后一层是纯线性的，所以 网络可以学会预测任意范围内的值。 注意，编译网络用的是 mse 损失函数，即均方误差（MSE，mean squared error），预测值与目标值之差的平方。这是回归问题常用的损失函数。 在训练过程中还监控一个新指标：平均绝对误差（MAE，mean absolute error）。它是预测值与目标值之差的绝对值。比如，如果这个问题的 MAE 等于 0.5，就表示你预测的房价与实际价格平均相差 500 美元。

3.5.4 利用 K 折验证来验证你的方法

为了在调节网络参数（比如训练的轮数）的同时对网络进行评估，你可以将数据划分为训 练集和验证集，正如前面例子中所做的那样。但由于数据点很少，验证集会非常小（比如大约 100 个样本）。因此，验证分数可能会有很大波动，这取决于你所选择的验证集和训练集。也就 是说，验证集的划分方式可能会造成验证分数上有很大的方差，这样就无法对模型进行可靠的评估。

在这种情况下，最佳做法是使用 K 折交叉验证（见图 3-11）。这种方法将可用数据划分为 K 个分区（K 通常取 4 或 5），实例化 K 个相同的模型，将每个模型在 K-1 个分区上训练，并在剩下的一个分区上进行评估。模型的验证分数等于 K 个验证分数的平均值。这种方法的代码实现很简单。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Z3WpEzHf-1671980336306)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225201650898.png)]

import numpy as np
k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []
for i in range(k):
    print('processing fold #', i)
    # 准备验证数据：第 k 个分区的数据
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
    
    # 准备训练数据：其他所有分区的数据
    partial_train_data = np.concatenate([train_data[:i * num_val_samples],
    									 train_data[(i + 1) * num_val_samples:]],
    									 axis=0)
    partial_train_targets = np.concatenate([train_targets[:i * num_val_samples],
    										train_targets[(i + 1) * num_val_samples:]],
											axis=0)
    # 构建 Keras 模型（已编译）
    model = build_model()
    
    # 训练模型（静默模式，verbose=0）
    model.fit(partial_train_data, partial_train_targets,
              epochs=num_epochs, batch_size=1, verbose=0)
    
    # 在验证数据上评估模型
    val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
    all_scores.append(val_mae)

设置 num_epochs = 100，运行结果如下。

all_scores 
# [2.588258957792037, 3.1289568449719116, 3.1856116051248984, 3.0763342615401386]
np.mean(all_scores)
# 2.9947904173572462 ,k = 4的平均验证结果

每次运行模型得到的验证分数有很大差异，从 2.6 到 3.2 不等。平均分数（3.0）是比单一 分数更可靠的指标——这就是 K 折交叉验证的关键。在这个例子中，预测的房价与实际价格平 均相差 3000 美元，考虑到实际价格范围在 10 000~50 000 美元，这一差别还是很大的。 我们让训练时间更长一点，达到 500 个轮次。为了记录模型在每轮的表现，我们需要修改训练循环，以保存每轮的验证分数记录。

保存每折的验证结果

num_epochs = 500
all_mae_histories = []
for i in range(k):
 print('processing fold #', i)
 # 准备验证数据：第 k 个分区的数据
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
    
    # 准备训练数据：其他所有分区的数据
    partial_train_data = np.concatenate([train_data[:i * num_val_samples],
    									 train_data[(i + 1) * num_val_samples:]],
    									 axis=0)
    partial_train_targets = np.concatenate([train_targets[:i * num_val_samples],
    										train_targets[(i + 1) * num_val_samples:]],
											axis=0)
    # 构建 Keras 模型（已编译）
    model = build_model()
    
    # 训练模型（静默模式，verbose=0）
	history = model.fit(partial_train_data, partial_train_targets,
						validation_data=(val_data, val_targets),
						epochs=num_epochs, batch_size=1, verbose=0)
    
    mae_history = history.history['val_mean_absolute_error']
	all_mae_histories.append(mae_history)

计算所有轮次中的 K 折验证分数平均值

average_mae_history = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

绘制验证分数

import matplotlib.pyplot as plt
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4PWycVc0-1671980336306)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225203043637.png)]

因为纵轴的范围较大，且数据方差相对较大，所以难以看清这张图的规律。我们来重新绘 制一张图。

• 删除前 10 个数据点，因为它们的取值范围与曲线上的其他点不同。
• 将每个数据点替换为前面数据点的指数移动平均值，以得到光滑的曲线。

绘制验证分数（删除前 10 个数据点）

def smooth_curve(points, factor=0.9):
	smoothed_points = []
    for point in points:
        if smoothed_points:
            previous = smoothed_points[-1]
            smoothed_points.append(previous * factor + point * (1 - factor))
    	else:
    		smoothed_points.append(point)
    	return smoothed_points
    
smooth_mae_history = smooth_curve(average_mae_history[10:])

plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

从图 3-13 可以看出，验证 MAE 在 80 轮后不再显著降低，之后就开始过拟合。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ThOVVohb-1671980336306)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225203207332.png)]

完成模型调参之后（除了轮数，还可以调节隐藏层大小），你可以使用最佳参数在所有训练数据上训练最终的生产模型，然后观察模型在测试集上的性能。

训练最终模型

model = build_model()
model.fit(train_data, train_targets,
		  epochs=80, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)

# 最终结果如下：
test_mae_score
# 2.5532484335057877

3.5.5 小结

下面是你应该从这个例子中学到的要点。

• 回归问题使用的损失函数与分类问题不同。回归常用的损失函数是均方误差（MSE）。

• 同样，回归问题使用的评估指标也与分类问题不同。显而易见，精度的概念不适用于回 归问题。常见的回归指标是平均绝对误差（MAE）。

• 如果输入数据的特征具有不同的取值范围，应该先进行预处理，对每个特征单独进行 缩放。

• 如果可用的数据很少，使用 K 折验证可以可靠地评估模型。

• 如果可用的训练数据很少，最好使用隐藏层较少（通常只有一到两个）的小型网络，以 避免严重的过拟合。

3.6 本章小结

• 在将原始数据输入神经网络之前，通常需要对其进行预处理。
• 如果数据特征具有不同的取值范围，那么需要进行预处理，将每个特征单独缩放。
• 随着训练的进行，神经网络最终会过拟合，并在前所未见的数据上得到更差的结果。
• 如果训练数据不是很多，应该使用只有一两个隐藏层的小型网络，以避免严重的过拟合。
• 如果数据被分为多个类别，那么中间层过小可能会导致信息瓶颈。
• 回归问题使用的损失函数和评估指标都与分类问题不同。
• 如果要处理的数据很少，K 折验证有助于可靠地评估模型。

4、机器学习基础

学完第 3 章的三个实例，你应该已经知道如何用神经网络解决分类问题和回归问题，而且 也看到了机器学习的核心难题：过拟合。本章会将你对这些问题的直觉固化为解决深度学习问 题的可靠的概念框架。我们将把所有这些概念——模型评估、数据预处理、特征工程、解决过拟合——整合为详细的七步工作流程，用来解决任何机器学习任务。

4.1 机器学习的四个分支

在前面的例子中，你已经熟悉了三种类型的机器学习问题：二分类问题、多分类问题和标 量回归问题。这三者都是监督学习（supervised learning）的例子，其目标是学习训练输入与训 练目标之间的关系。

监督学习只是冰山一角——机器学习是非常宽泛的领域，其子领域的划分非常复杂。机器 学习算法大致可分为四大类，我们将在接下来的四小节中依次介绍。

4.1.1 监督学习

监督学习是目前最常见的机器学习类型。给定一组样本（通常由人工标注），它可以学会将 输入数据映射到已知目标［也叫标注（annotation）］。本书前面的四个例子都属于监督学习。一 般来说，近年来广受关注的深度学习应用几乎都属于监督学习，比如光学字符识别、语音识别、 图像分类和语言翻译。

虽然监督学习主要包括分类和回归，但还有更多的奇特变体，主要包括如下几种。

• 序列生成（sequence generation）。给定一张图像，预测描述图像的文字。序列生成有时可以被重新表示为一系列分类问题，比如反复预测序列中的单词或标记。
• 语法树预测（syntax tree prediction）。给定一个句子，预测其分解生成的语法树。
• 目标检测（object detection）。给定一张图像，在图中特定目标的周围画一个边界框。这 个问题也可以表示为分类问题（给定多个候选边界框，对每个框内的目标进行分类）或分类与回归联合问题（用向量回归来预测边界框的坐标）。
• 图像分割（image segmentation）。给定一张图像，在特定物体上画一个像素级的掩模（mask）。

4.1.2 无监督学习

无监督学习是指在没有目标的情况下寻找输入数据的有趣变换，其目的在于数据可视化、 数据压缩、数据去噪或更好地理解数据中的相关性。无监督学习是数据分析的必备技能，在解决监督学习问题之前，为了更好地了解数据集，它通常是一个必要步骤。降维（dimensionality reduction）和聚类（clustering）都是众所周知的无监督学习方法。

4.1.3 自监督学习

自监督学习是监督学习的一个特例，它与众不同，值得单独归为一类。自监督学习是没有 人工标注的标签的监督学习，你可以将它看作没有人类参与的监督学习。标签仍然存在（因为 总要有什么东西来监督学习过程），但它们是从输入数据中生成的，通常是使用启发式算法生成的。

举个例子，自编码器（autoencoder）是有名的自监督学习的例子，其生成的目标就是未经修改的输入。同样，给定视频中过去的帧来预测下一帧，或者给定文本中前面的词来预测下一个词， 都是自监督学习的例子［这两个例子也属于时序监督学习（temporally supervised learning），即用 未来的输入数据作为监督］。注意，监督学习、自监督学习和无监督学习之间的区别有时很模糊， 这三个类别更像是没有明确界限的连续体。自监督学习可以被重新解释为监督学习或无监督学 习，这取决于你关注的是学习机制还是应用场景。

4.1.4 强化学习

在强化学习中，智能体（agent）接收有关其环境的信息，并学会选择使某种奖励最大化的行动。目前，强化学习主要集中在研究领域，除游戏外还没有取得实践上的重大成功。但是，我 们期待强化学习未来能够实现越来越多的实际应用：自动驾驶汽车、机器人、资源管理、教育等。 强化学习的时代已经到来，或即将到来。

4.2 评估机器学习模型

在第 3 章介绍的三个例子中，我们将数据划分为训练集、验证集和测试集。我们没有在训 练模型的相同数据上对模型进行评估，其原因很快显而易见：仅仅几轮过后，三个模型都开始过拟合。也就是说，随着训练的进行，模型在训练数据上的性能始终在提高，但在前所未见的 数据上的性能则不再变化或者开始下降。

机器学习的目的是得到可以泛化（generalize）的模型，即在前所未见的数据上表现很好的模型，而过拟合则是核心难点。你只能控制可以观察的事情，所以能够可靠地衡量模型的泛化 能力非常重要。后面几节将介绍降低过拟合以及将泛化能力最大化的方法。本节重点介绍如何 衡量泛化能力，即如何评估机器学习模型。

4.2.1 训练集、验证集和测试集

评估模型的重点是将数据划分为三个集合：训练集、验证集和测试集。在训练数据上训练 模型，在验证数据上评估模型。一旦找到了最佳参数，就在测试数据上最后测试一次。

你可能会问，为什么不是两个集合：一个训练集和一个测试集？在训练集上训练模型，然 后在测试集上评估模型。这样简单得多！

原因在于开发模型时总是需要调节模型配置，比如选择层数或每层大小［这叫作模型的超参数（hyperparameter），以便与模型参数（即权重）区分开］。这个调节过程需要使用模型在验证数据上的性能作为反馈信号。这个调节过程本质上就是一种学习：在某个参数空间中寻找良好的模型配置。因此，如果基于模型在验证集上的性能来调节模型配置，会很快导致模型在验 证集上过拟合，即使你并没有在验证集上直接训练模型也会如此。

造成这一现象的关键在于信息泄露（information leak）。每次基于模型在验证集上的性能来 调节模型超参数，都会有一些关于验证数据的信息泄露到模型中。如果对每个参数只调节一次， 那么泄露的信息很少，验证集仍然可以可靠地评估模型。但如果你多次重复这一过程（运行一 次实验，在验证集上评估，然后据此修改模型），那么将会有越来越多的关于验证集的信息泄露 到模型中。

最后，你得到的模型在验证集上的性能非常好（人为造成的），因为这正是你优化的目的。 你关心的是模型在全新数据上的性能，而不是在验证数据上的性能，因此你需要使用一个完全 不同的、前所未见的数据集来评估模型，它就是测试集。你的模型一定不能读取与测试集有关 的任何信息，既使间接读取也不行。如果基于测试集性能来调节模型，那么对泛化能力的衡量 是不准确的。

将数据划分为训练集、验证集和测试集可能看起来很简单，但如果可用数据很少，还有几 种高级方法可以派上用场。我们先来介绍三种经典的评估方法：简单的留出验证、K 折验证， 以及带有打乱数据的重复 K 折验证。

1. 简单的留出验证

留出一定比例的数据作为测试集。在剩余的数据上训练模型，然后在测试集上评估模型。 如前所述，为了防止信息泄露，你不能基于测试集来调节模型，所以还应该保留一个验证集。

留出验证（hold-out validation）的示意图见图 4-1。代码清单 4-1 给出了其简单实现。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2acTZOM6-1671980336306)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225215613461.png)]

num_validation_samples = 10000
np.random.shuffle(data)		# 通常需要打乱数据
validation_data = data[:num_validation_samples]	# 定义验证集
data = data[num_validation_samples:]	# 定义训练集
training_data = data[:]	
# 在训练数据上训练模型，并在验证数据上评估模型
model = get_model()
model.train(training_data)
validation_score = model.evaluate(validation_data)
# 现在你可以调节模型、重新训练、评估，然后再次调节……
model = get_model()
model.train(np.concatenate([training_data,
 validation_data]))
# 一旦调节好超参数，通常就在所有非测试数据上从头开始训练最终模型
test_score = model.evaluate(test_data)

这是最简单的评估方法，但有一个缺点：如果可用的数据很少，那么可能验证集和测试集 包含的样本就太少，从而无法在统计学上代表数据。这个问题很容易发现：如果在划分数据前 进行不同的随机打乱，最终得到的模型性能差别很大，那么就存在这个问题。接下来会介绍 K 折 验证与重复的 K 折验证，它们是解决这一问题的两种方法。

2. K 折验证

K 折验证（K-fold validation）将数据划分为大小相同的 K 个分区。对于每个分区 i，在剩余的 K-1 个分区上训练模型，然后在分区 i 上评估模型。最终分数等于 K 个分数的平均值。对 于不同的训练集 - 测试集划分，如果模型性能的变化很大，那么这种方法很有用。与留出验证 一样，这种方法也需要独立的验证集进行模型校正。

K 折交叉验证的示意图见图 4-2。代码清单 4-2 给出了其简单实现。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lmaO5Fe5-1671980336307)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225215825744.png)]

k = 4
num_validation_samples = len(data) // k
np.random.shuffle(data)
validation_scores = []
for fold in range(k):
	validation_data = data[num_validation_samples * fold: 
        # 选择验证数据分区
		num_validation_samples * (fold + 1)]
    	# 使用剩余数据作为训练数据。注意，+ 运算符是列表合并，不是求和
		training_data = data[:num_validation_samples * fold] +
						data[num_validation_samples * (fold + 1):]
        # 创建一个全新的模型实例（未训练）
		model = get_model()
		model.train(training_data)
		validation_score = model.evaluate(validation_data)
		validation_scores.append(validation_score)
# 最终验证分数：K 折验证分数的平均值
validation_score = np.average(validation_scores) 
# 在所有非测试数据上训练最终模型
model = get_model()
model.train(data)
test_score = model.evaluate(test_data)

3. 带有打乱数据的重复 K 折验证

如果可用的数据相对较少，而你又需要尽可能精确地评估模型，那么可以选择带有打乱数 据的重复 K 折验证（iterated K-fold validation with shuffling）。我发现这种方法在 Kaggle 竞赛中 特别有用。具体做法是多次使用 K 折验证，在每次将数据划分为 K 个分区之前都先将数据打乱。 最终分数是每次 K 折验证分数的平均值。注意，这种方法一共要训练和评估 P×K 个模型（P 是重复次数），计算代价很大。

4.2.2 评估模型的注意事项

选择模型评估方法时，需要注意以下几点。

数据代表性（data representativeness）。你希望训练集和测试集都能够代表当前数据。例如，你想要对数字图像进行分类，而图像样本是按类别排序的，如果你将前 80% 作为训 练集，剩余 20% 作为测试集，那么会导致训练集中只包含类别 0~7，而测试集中只包含 类别 8~9。这个错误看起来很可笑，却很常见。因此，在将数据划分为训练集和测试集之前，通常应该随机打乱数据。

时间箭头（the arrow of time）。如果想要根据过去预测未来（比如明天的天气、股票走势 等），那么在划分数据前你不应该随机打乱数据，因为这么做会造成时间泄露（temporal leak）：你的模型将在未来数据上得到有效训练。在这种情况下，你应该始终确保测试集 中所有数据的时间都晚于训练集数据。

数据冗余（redundancy in your data）。如果数据中的某些数据点出现了两次（这在现实中的数据里十分常见），那么打乱数据并划分成训练集和验证集会导致训练集和验证集之 间的数据冗余。从效果上来看，你是在部分训练数据上评估模型，这是极其糟糕的！一 定要确保训练集和验证集之间没有交集。

4.3 数据预处理、特征工程和特征学习

除模型评估之外，在深入研究模型开发之前，我们还必须解决另一个重要问题：将数据输 入神经网络之前，如何准备输入数据和目标？许多数据预处理方法和特征工程技术都是和特定 领域相关的（比如只和文本数据或图像数据相关），我们将在后续章节的实例中介绍这些内容。 现在我们要介绍所有数据领域通用的基本方法。

4.3.1 神经网络的数据预处理

数据预处理的目的是使原始数据更适于用神经网络处理，包括向量化、标准化、处理缺失 值和特征提取。

1. 向量化

神经网络的所有输入和目标都必须是浮点数张量（在特定情况下可以是整数张量）。无论处理什么数据（声音、图像还是文本），都必须首先将其转换为张量，这一步叫作数据向量化 （data vectorization）。例如，在前面两个文本分类的例子中，开始时文本都表示为整数列表（代表单词序列），然后我们用 one-hot 编码将其转换为 float32 格式的张量。在手写数字分类和预测房价的例子中，数据已经是向量形式，所以可以跳过这一步。

2. 值标准化

在手写数字分类的例子中，开始时图像数据被编码为 0~255 范围内的整数，表示灰度值。 将这一数据输入网络之前，你需要将其转换为 float32 格式并除以 255，这样就得到 0~1 范围内的浮点数。同样，预测房价时，开始时特征有各种不同的取值范围，有些特征是较小的浮点数， 有些特征是相对较大的整数。将这一数据输入网络之前，你需要对每个特征分别做标准化，使 其均值为 0、标准差为 1。

一般来说，将取值相对较大的数据（比如多位整数，比网络权重的初始值大很多）或异质 数据（heterogeneous data，比如数据的一个特征在 0~1 范围内，另一个特征在 100~200 范围内） 输入到神经网络中是不安全的。这么做可能导致较大的梯度更新，进而导致网络无法收敛。为 了让网络的学习变得更容易，输入数据应该具有以下特征。

• 取值较小：大部分值都应该在 0~1 范围内。

• 同质性（homogenous）：所有特征的取值都应该在大致相同的范围内。

  此外，下面这种更严格的标准化方法也很常见，而且很有用，虽然不一定总是必需的（例如， 对于数字分类问题就不需要这么做）。

• 将每个特征分别标准化，使其平均值为 0。

• 将每个特征分别标准化，使其标准差为 1。

# 假设 x 是一个形状为 (samples, features) 的二维矩阵
x -= x.mean(axis=0)
x /= x.std(axis=0)

3. 处理缺失值

你的数据中有时可能会有缺失值。例如在房价的例子中，第一个特征（数据中索引编号为 0 的列）是人均犯罪率。如果不是所有样本都具有这个特征的话，怎么办？那样你的训练数据 或测试数据将会有缺失值。

一般来说，对于神经网络，将缺失值设置为 0 是安全的，只要 0 不是一个有意义的值。网 络能够从数据中学到 0 意味着缺失数据，并且会忽略这个值。

注意，如果测试数据中可能有缺失值，而网络是在没有缺失值的数据上训练的，那么网络 不可能学会忽略缺失值。在这种情况下，你应该人为生成一些有缺失项的训练样本：多次复制 一些训练样本，然后删除测试数据中可能缺失的某些特征。

4.3.2 特征工程

特征工程（feature engineering）是指将数据输入模型之前，利用你自己关于数据和机器学 习算法（这里指神经网络）的知识对数据进行硬编码的变换（不是模型学到的），以改善模型的效果。多数情况下，一个机器学习模型无法从完全任意的数据中进行学习。呈现给模型的数据应该便于模型进行学习。

我们来看一个直观的例子。假设你想开发一个模型，输入一个时钟图像，模型能够输出对应的时间（见图 4-3）。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7TskN8Tb-1671980336307)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225222118991.png)]

如果你选择用图像的原始像素作为输入数据，那么这个机器学习问题将非常困难。你需要 用卷积神经网络来解决这个问题，而且还需要花费大量的计算资源来训练网络。

但如果你从更高的层次理解了这个问题（你知道人们怎么看时钟上的时间），那么可以为机 器学习算法找到更好的输入特征，比如你可以编写 5 行 Python 脚本，找到时钟指针对应的黑色 像素并输出每个指针尖的 (x, y) 坐标，这很简单。然后，一个简单的机器学习算法就可以学会这 些坐标与时间的对应关系。

你还可以进一步思考：进行坐标变换，将 (x, y) 坐标转换为相对于图像中心的极坐标。这样 输入就变成了每个时钟指针的角度 theta。现在的特征使问题变得非常简单，根本不需要机器 学习，因为简单的舍入运算和字典查找就足以给出大致的时间。

这就是特征工程的本质：用更简单的方式表述问题，从而使问题变得更容易。它通常需要 深入理解问题。

深度学习出现之前，特征工程曾经非常重要，因为经典的浅层算法没有足够大的假设空间 来自己学习有用的表示。将数据呈现给算法的方式对解决问题至关重要。例如，卷积神经网络 在 MNIST 数字分类问题上取得成功之前，其解决方法通常是基于硬编码的特征，比如数字图像 中的圆圈个数、图像中每个数字的高度、像素值的直方图等。

幸运的是，对于现代深度学习，大部分特征工程都是不需要的，因为神经网络能够从原始 数据中自动提取有用的特征。这是否意味着，只要使用深度神经网络，就无须担心特征工程呢？ 并不是这样，原因有两点。

• 良好的特征仍然可以让你用更少的资源更优雅地解决问题。例如，使用卷积神经网络来 读取钟面上的时间是非常可笑的。

• 良好的特征可以让你用更少的数据解决问题。深度学习模型自主学习特征的能力依赖于 大量的训练数据。如果只有很少的样本，那么特征的信息价值就变得非常重要。

4.4 过拟合与欠拟合

机器学习的根本问题是优化和泛化之间的对立。优化（optimization）是指调节模型以在训 练数据上得到最佳性能（即机器学习中的学习），而泛化（generalization）是指训练好的模型在 前所未见的数据上的性能好坏。机器学习的目的当然是得到良好的泛化，但你无法控制泛化， 只能基于训练数据调节模型。

训练开始时，优化和泛化是相关的：训练数据上的损失越小，测试数据上的损失也越小。 这时的模型是欠拟合（underfit）的，即仍有改进的空间，网络还没有对训练数据中所有相关模 式建模。但在训练数据上迭代一定次数之后，泛化不再提高，验证指标先是不变，然后开始变差， 即模型开始过拟合（overfit）。这时模型开始学习仅和训练数据有关的模式，但这种模式对新数据来说是错误的或无关紧要的。

为了防止模型从训练数据中学到错误或无关紧要的模式，最优解决方法是获取更多的训练 数据。模型的训练数据越多，泛化能力自然也越好。如果无法获取更多数据，次优解决方法是调节模型允许存储的信息量，或对模型允许存储的信息加以约束。如果一个网络只能记住几个模式，那么优化过程会迫使模型集中学习最重要的模式，这样更可能得到良好的泛化。

这种降低过拟合的方法叫作正则化（regularization）。我们先介绍几种最常见的正则化方法， 然后将其应用于实践中，以改进 3.4 节的电影分类模型。

4.4.1 减小网络大小

防止过拟合的最简单的方法就是减小模型大小，即减少模型中可学习参数的个数（这由层 数和每层的单元个数决定）。在深度学习中，模型中可学习参数的个数通常被称为模型的容量 （capacity）。直观上来看，参数更多的模型拥有更大的记忆容量（memorization capacity），因此能 够在训练样本和目标之间轻松地学会完美的字典式映射，这种映射没有任何泛化能力。

始终牢记：深度学习模型通常都很擅长拟合训练数据，但真正的挑战在于泛化，而不是拟合。

与此相反，如果网络的记忆资源有限，则无法轻松学会这种映射。因此，为了让损失最小化，网络必须学会对目标具有很强预测能力的压缩表示，这也正是我们感兴趣的数据表示。同时请记住，你使用的模型应该具有足够多的参数，以防欠拟合，即模型应避免记忆资源不足。在容量过大与容量不足之间要找到一个折中。

不幸的是，没有一个魔法公式能够确定最佳层数或每层的最佳大小。你必须评估一系列不 同的网络架构（当然是在验证集上评估，而不是在测试集上），以便为数据找到最佳的模型大小。 要找到合适的模型大小，一般的工作流程是开始时选择相对较少的层和参数，然后逐渐增加层的大小或增加新层，直到这种增加对验证损失的影响变得很小。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XpanYX7S-1671980336307)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225223049678.png)]

4.4.2 添加权重正则化

一种常见的降低过拟合的方法就是强制让模型权重只能取较小的值， 从而限制模型的复杂度，这使得权重值的分布更加规则（regular）。这种方法叫作权重正则化 （weight regularization），其实现方法是向网络损失函数中添加与较大权重值相关的成本（cost）。 这个成本有两种形式。

• L1 正则化（L1 regularization）：添加的成本与权重系数的绝对值［权重的 L1 范数（norm）］成正比。
• L2 正则化（L2 regularization）：添加的成本与权重系数的平方（权重的 L2 范数）成正比。 神经网络的 L2 正则化也叫权重衰减（weight decay），权重衰减 与 L2 正则化在数学上是完全相同的。

在 Keras 中，添加权重正则化的方法是向层传递权重正则化项实例（weight regularizer instance）作为关键字参数。下列代码将向电影评论分类网络中添加 L2 权重正则化。

from keras import regularizers
model = models.Sequential()
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
 		  activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
 		  activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

l2(0.001) 的意思是该层权重矩阵的每个系数都会使网络总损失增加 0.001 * weight_ coefficient_value。注意，由于这个惩罚项只在训练时添加，所以这个网络的训练损失会 比测试损失大很多。

图 4-7 显示了 L2 正则化惩罚的影响。如你所见，即使两个模型的参数个数相同，具有 L2 正则化的模型（圆点）比参考模型（十字）更不容易过拟合。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tQi9KTiZ-1671980336307)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225223028326.png)]

你还可以用 Keras 中以下这些权重正则化项来代替 L2 正则化。

from keras import regularizers
regularizers.l1(0.001)					# L1 正则化
regularizers.l1_l2(l1=0.001, l2=0.001)	# 同时做 L1 和 L2 正则化

4.4.3 添加 dropout 正则化

dropout 是神经网络最有效也最常用的正则化方法之一，对某一层使用 dropout，就是在训练过程中随机将该层的一些输出特征舍 弃（设置为 0）。假设在训练过程中，某一层对给定输入样本的返回值应该是向量 [0.2, 0.5, 1.3, 0.8, 1.1]。使用 dropout 后，这个向量会有几个随机的元素变成 0，比如 [0, 0.5, 1.3, 0, 1.1]。dropout 比率（dropout rate）是被设为 0 的特征所占的比例，通常在 0.2~0.5 范围内。测试时没有单元被舍弃，而该层的输出值需要按 dropout 比率缩小，因为这时比训练时有更多的单元被激活，需要加以平衡。

假设有一个包含某层输出的 Numpy 矩 阵 layer_output，其形状为 (batch_size, features)。训练时，我们随机将矩阵中一部分值设为 0。

layer_output *= np.random.randint(0, high=2, size=layer_output.shape)
# 训练时，舍弃 50%的输出单元

测试时，我们将输出按 dropout 比率缩小。这里我们乘以 0.5（因为前面舍弃了一半的单元）。

layer_output *= 0.5		# 测试时

注意，为了实现这一过程，还可以让两个运算都在训练时进行，而测试时输出保持不变。 这通常也是实践中的实现方式（见图 4-8）。

layer_output *= np.random.randint(0, high=2, size=layer_output.shape)	# 训练时
layer_output /= 0.5		# 注意，是成比例放大而不是成比例缩小

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mGWROcOs-1671980336307)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225223836916.png)]

在 Keras 中，你可以通过 Dropout 层向网络中引入 dropout，dropout 将被应用于前面一层的输出。

向 IMDB 网络中添加 dropout

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))

图 4-9 给出了结果的图示。我们再次看到，这种方法的性能相比参考网络有明显提高。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-32kcDs0G-1671980336308)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225223938331.png)]

总结一下，防止神经网络过拟合的常用方法包括：

• 获取更多的训练数据
• 减小网络容量
• 添加权重正则化
• 添加 dropout

4.5 机器学习的通用工作流程

本节将介绍一种可用于解决任何机器学习问题的通用模板。这一模板将你在本章学到的这 些概念串在一起：问题定义、评估、特征工程和解决过拟合。

4.5.1 定义问题，收集数据集

首先，你必须定义所面对的问题。

• 你的输入数据是什么？你要预测什么？只有拥有可用的训练数据，你才能学习预测某件事情。比如，只有同时拥有电影评论和情感标注，你才能学习对电影评论进行情感分类。 因此，数据可用性通常是这一阶段的限制因素（除非你有办法付钱让人帮你收集数据）。
• 你面对的是什么类型的问题？是二分类问题、多分类问题、标量回归问题、向量回归问题， 还是多分类、多标签问题？或者是其他问题，比如聚类、生成或强化学习？确定问题类型有助于你选择模型架构、损失函数等。

只有明确了输入、输出以及所使用的数据，你才能进入下一阶段。注意你在这一阶段所做的假设。

• 假设输出是可以根据输入进行预测的。
• 假设可用数据包含足够多的信息，足以学习输入和输出之间的关系。

在开发出工作模型之前，这些只是假设，等待验证真假。并非所有问题都可以解决。你收 集了包含输入 X 和目标 Y 的很多样例，并不意味着 X 包含足够多的信息来预测 Y。例如，如果 你想根据某支股票最近的历史价格来预测其股价走势，那你成功的可能性不大，因为历史价格 并没有包含很多可用于预测的信息。

有一类无法解决的问题你应该知道，那就是非平稳问题（nonstationary problem）。假设你想 要构建一个服装推荐引擎，并在一个月（八月）的数据上训练，然后在冬天开始生成推荐结果。 一个大问题是，人们购买服装的种类是随着季节变化的，即服装购买在几个月的尺度上是一个 非平稳现象。你想要建模的对象随着时间推移而改变。在这种情况下，正确的做法是不断地利 用最新数据重新训练模型，或者在一个问题是平稳的时间尺度上收集数据。对于服装购买这种 周期性问题，几年的数据足以捕捉到季节性变化，但一定要记住，要将一年中的时间作为模型的一个输入。

请记住，机器学习只能用来记忆训练数据中存在的模式。你只能识别出曾经见过的东西。 在过去的数据上训练机器学习来预测未来，这里存在一个假设，就是未来的规律与过去相同。 但事实往往并非如此。

4.5.2 选择衡量成功的指标

要控制一件事物，就需要能够观察它。要取得成功，就必须给出成功的定义：精度？准确 率（precision）和召回率（recall）？客户保留率？衡量成功的指标将指引你选择损失函数，即 模型要优化什么。它应该直接与你的目标（如业务成功）保持一致。

对于平衡分类问题（每个类别的可能性相同），精度和接收者操作特征曲线下面积（area under the receiver operating characteristic curve，ROC AUC）是常用的指标。对于类别不平衡的问题，你可以使用准确率和召回率。对于排序问题或多标签分类，你可以使用平均准确率均值 （mean average precision）。自定义衡量成功的指标也很常见。要想了解各种机器学习的成功衡量 指标以及这些指标与不同问题域的关系，你可以浏览 Kaggle 网站上的数据科学竞赛，上面展示 了各种各样的问题和评估指标。

4.5.3 确定评估方法

一旦明确了目标，你必须确定如何衡量当前的进展。前面介绍了三种常见的评估方法。

• 留出验证集。数据量很大时可以采用这种方法。
• K 折交叉验证。如果留出验证的样本量太少，无法保证可靠性，那么应该选择这种方法。
• 重复的 K 折验证。如果可用的数据很少，同时模型评估又需要非常准确，那么应该使用这种方法。

只需选择三者之一。大多数情况下，第一种方法足以满足要求。

4.5.4 准备数据

一旦知道了要训练什么、要优化什么以及评估方法，那么你就几乎已经准备好训练模型了。 但首先你应该将数据格式化，使其可以输入到机器学习模型中（这里假设模型为深度神经网络）。

• 如前所述，应该将数据格式化为张量。
• 这些张量的取值通常应该缩放为较小的值，比如在 [-1, 1] 区间或 [0, 1] 区间。
• 如果不同的特征具有不同的取值范围（异质数据），那么应该做数据标准化。
• 你可能需要做特征工程，尤其是对于小数据问题。 准备好输入数据和目标数据的张量后，你就可以开始训练模型了。

4.5.5 开发比基准更好的模型

这一阶段的目标是获得统计功效（statistical power），即开发一个小型模型，它能够打败纯 随机的基准（dumb baseline）。在 MNIST 数字分类的例子中，任何精度大于 0.1 的模型都可以说 具有统计功效；在 IMDB 的例子中，任何精度大于 0.5 的模型都可以说具有统计功效。

注意，不一定总是能获得统计功效。如果你尝试了多种合理架构之后仍然无法打败随机基准， 那么原因可能是问题的答案并不在输入数据中。要记住你所做的两个假设。

• 假设输出是可以根据输入进行预测的。
• 假设可用的数据包含足够多的信息，足以学习输入和输出之间的关系。

如果一切顺利，你还需要选择三个关键参数来构建第一个工作模型。

• 最后一层的激活。它对网络输出进行有效的限制。例如，IMDB 分类的例子在最后一层 使用了 sigmoid，回归的例子在最后一层没有使用激活，等等。
• 损失函数。它应该匹配你要解决的问题的类型。例如，IMDB 的例子使用 binary_ crossentropy、回归的例子使用 mse，等等。
• 优化配置。你要使用哪种优化器？学习率是多少？大多数情况下，使用 rmsprop 及其 默认的学习率是稳妥的。

关于损失函数的选择，需要注意，直接优化衡量问题成功的指标不一定总是可行的。有时 难以将指标转化为损失函数，要知道，损失函数需要在只有小批量数据时即可计算（理想情况 下，只有一个数据点时，损失函数应该也是可计算的），而且还必须是可微的（否则无法用反向传播来训练网络）。例如，广泛使用的分类指标 ROC AUC 就不能被直接优化。因此在分类任务 中，常见的做法是优化 ROC AUC 的替代指标，比如交叉熵。一般来说，你可以认为交叉熵越小， ROC AUC 越大。

表 4-1 列出了常见问题类型的最后一层激活和损失函数，可以帮你进行选择。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MUJ7pylz-1671980336308)(C:\Users\10555\AppData\Roaming\Typora\typora-user-images\image-20221225224831011.png)]

4.5.6 扩大模型规模：开发过拟合的模型

一旦得到了具有统计功效的模型，问题就变成了：模型是否足够强大？它是否具有足够多 的层和参数来对问题进行建模？例如，只有单个隐藏层且只有两个单元的网络，在 MNIST 问题 上具有统计功效，但并不足以很好地解决问题。请记住，机器学习中无处不在的对立是优化和 泛化的对立，理想的模型是刚好在欠拟合和过拟合的界线上，在容量不足和容量过大的界线上。 为了找到这条界线，你必须穿过它。

要搞清楚你需要多大的模型，就必须开发一个过拟合的模型，这很简单。

• 添加更多的层。
• 让每一层变得更大。
• 训练更多的轮次。

要始终监控训练损失和验证损失，以及你所关心的指标的训练值和验证值。如果你发现模型在验证数据上的性能开始下降，那么就出现了过拟合。 下一阶段将开始正则化和调节模型，以便尽可能地接近理想模型，既不过拟合也不欠拟合。

4.5.7 模型正则化与调节超参数

这一步是最费时间的：你将不断地调节模型、训练、在验证数据上评估（这里不是测试数据）、 再次调节模型，然后重复这一过程，直到模型达到最佳性能。你应该尝试以下几项。

• 添加 dropout。
• 尝试不同的架构：增加或减少层数。
• 添加 L1 和 / 或 L2 正则化。
• 尝试不同的超参数（比如每层的单元个数或优化器的学习率），以找到最佳配置。
• 反复做特征工程（可选）：添加新特征或删除没有信息量的特征。

请注意：每次使用验证过程的反馈来调节模型，都会将有关验证过程的信息泄露到模型中。 如果只重复几次，那么无关紧要；但如果系统性地迭代许多次，最终会导致模型对验证过程过 拟合（即使模型并没有直接在验证数据上训练）。这会降低验证过程的可靠性。

一旦开发出令人满意的模型配置，你就可以在所有可用数据（训练数据 + 验证数据）上训 练最终的生产模型，然后在测试集上最后评估一次。如果测试集上的性能比验证集上差很多， 那么这可能意味着你的验证流程不可靠，或者你在调节模型参数时在验证数据上出现了过拟合。 在这种情况下，你可能需要换用更加可靠的评估方法，比如重复的 K 折验证。

4.6 本章小结

• 定义问题与要训练的数据。收集这些数据，有需要的话用标签来标注数据。
• 选择衡量问题成功的指标。你要在验证数据上监控哪些指标？
• 确定评估方法：留出验证？ K 折验证？你应该将哪一部分数据用于验证？
• 开发第一个比基准更好的模型，即一个具有统计功效的模型。
• 开发过拟合的模型。
• 基于模型在验证数据上的性能来进行模型正则化与调节超参数。许多机器学习研究往往 只关注这一步，但你一定要牢记整个工作流程。
  数据问题。 准备好输入数据和目标数据的张量后，你就可以开始训练模型了。