ReBudget:通过运行时重新分配预算的方法,在基于市场的多核资源分配中权衡效率与公平性
ReBudget:通过运行时重新分配预算的方法,在基于市场的多核资源分配中权衡效率与公平性
摘要
在计算机系统中有效地分配共享资源是优化执行的关键。近日,一系列基于市场的解决方案被提出来解决这个问题。其中一些理论为市场均衡下的效率和/或公平损失提供了可证明的理论边界。然而,它们仅限于具有潜在重要约束的市场,如所有参与者拥有相等的预算,或将参与者的效用曲线拟合到特定的函数类型中。此外,它们通常没有提供一个直观的“旋钮”来控制效率与公平。
本文引入了市场效用范围(MUR)和市场预算范围(MBR)两个新指标,首次给出了任意预算分配下市场均衡的效率和公平性的理论边界。我们利用这一结果并提出 R e B u d g e t ReBudget ReBudget,这是一种迭代预算重新分配算法,可用于控制运行时的效率与公平。我们将该算法应用于多核芯片上的多资源分配问题。我们使用详细的执行驱动仿真进行的评估表明,我们的预算重新分配技术是直观、有效和高效的
1、介绍
设计可扩展的多核芯片(CMP)是即将到来的多核时代的一个重要目标。可扩展性的一个关键挑战是,这些核心将共享硬件资源,包括片上缓存、引脚带宽、芯片的功率预算等。先前的研究表明,自由争夺共享资源会损害系统性能。因此,在核心之间有效地分配资源是十分关键的。
不幸的是,由于无法对资源之间的交互进行建模,单一资源,以及更普遍的不协调的资源分配,可能不是最优的。已经提出的来协调跨多个资源的分配的一些解决方案,它们的性能估计方法包括试运行,人工神经网络,以及分析模型。不幸的是,这些都依赖于中心化机制(例如, g l o b a l h i l l − c l i m b i n g global\ hill-climbing global hill−climbing)来优化系统吞吐量,本质上是依次探索全局搜索空间,这可能是代价很大的,特别是在大规模系统中。
最近,又出现了一些基于市场的方法。Chase等人提出了一个静态市场,每个参与者向资源供应商透露愿意支付的金额,作为分配服务单位的函数,然后中央市场分配可用的计算资源,使资金利润最大化。然而,由于这个最大化的过程是由供应商中心化完成的,它能否有效地处理一个大规模的系统尚不清楚。
在分布式计算集群的背景下,Lai等人提出了一种基于市场的资源分配解决方案,允许参与者根据其他人对该资源的出价动态地调整自己的出价。资源分配是在很大程度上以分布式的方式完成的,这使得系统比中心化方法能够更好地进行扩展。最近,在我们的XChange工作中,我们也在CMP的背景下提出了一个这样的动态市场,并展示了XChange的可扩展性,它在很大程度上也是分布式的:CMP中的每个核心在很大程度上独立地、局部地积极优化其资源分配,而不是在全局上进行资源分配决策,以及通过相对简单的定价策略调和了参与者的需求。
XChange还表明,它可以很好地平衡系统效率和公平性。然而,这项研究是纯经验性的,它并不能保证效率和公平的损失。例如,众所周知,均衡中的市场机制有时可能是非常低效的,这被称为公地悲剧( T r a g e d y o f C o m m o n s Tragedy\ of\ Commons Tragedy of Commons)。因此,许多研究工作都集中在量化与最优资源分配相比的效率损失,这被称为纳什均衡(PoA)。例如,Zhang研究了一个所有参与者都有相同数量的金钱(预算)购买资源的市场,他发现在这样的市场中,系统的整体效率可能很低(最大可行效用的1/√N,其中N是市场参与者的数量),但公平性很高( ( 0.828 − a p p r o x i m a t e e n v y − f r e e 0.828-approximate\ envy-free 0.828−approximate envy−free,公平性的衡量标准)。这与我们在XChange工作中的经验观察是一致的。最近,Zahedi和Lee为cmp提出了一种名为弹性比例( e l a s t i c p r o p o r t i o n a l , E P elastic proportional, EP elasticproportional,EP)的资源分配机制,该机制确实提供了如帕累托效率、无嫉妒等博弈论保证。然而,这种保证依赖于这样一个假设,即应用程序的效用可以精确地曲线拟合到柯布-道格拉斯函数中,其中的系数被用作资源的“弹性”。我们的XChange工作表明,当这种曲线拟合不太适合应用时,EP实际上可能比预期的表现更差。此外,虽然EP被证明是符合帕累托效率的,但它相较全局最优的效率损失没有量化。
为了提高系统效率,同时牺牲一些公平性,我们的XChange工作讨论了一种 w e a l t h r e d i s t r i b u t i o n wealth \ redistribution wealth redistribution技术,它根据估计参与者的性能收益潜力来改变参与者的预算。然而,XChange的 w e a l t h r e d i s t r i b u t i o n wealth \ redistribution wealth redistribution是一种开/关技术,没有提供“旋钮”来控制效率与公平的权衡。它也没有得到一个可以为这种权衡提供边界的理论结果的支持。据我们所知,目前没有任何理论研究能够量化任意预算分配下效率和公平的损失。
贡献
这篇论文的贡献如下:
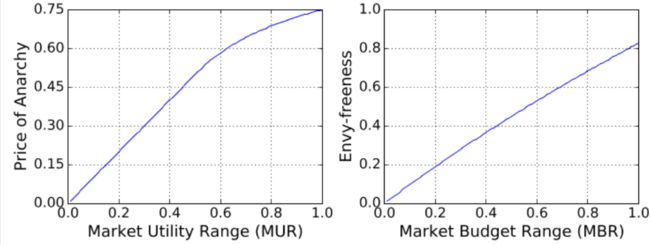
1️⃣ 我们介绍了一个新的指标:市场效用范围(MUR)——建立了在有限预算下市场均衡效率损失的理论界限。特别地,如果 M U R ≥ 0.5 MUR≥0.5 MUR≥0.5,则 P o A ≥ ( 1 − 1 4 M U R ) PoA\ge(1-\frac{1}{4MUR}) PoA≥(1−4MUR1)(即保证效率至少为最优配置的50%);如果 M U R < 0.5 MUR<0.5 MUR<0.5,则 P o A ≥ M U R PoA\ge MUR PoA≥MUR
2️⃣ 我们介绍了一个新的指标:市场预算范围(MBR)——建立了在有限预算下市场均衡公平性损失的理论界限。结果显示:任何的市场均衡是 ( 2 1 + M B R − 2 ) − a p p r o x i m a t e e n v y − f r e e (2\sqrt{1+MBR}-2)-approximate\ envy-free (21+MBR−2)−approximate envy−free。
3️⃣ 我们提出了 R e b u d g e t Rebudget Rebudget,这是一种重新分配预算的技术,能够以一种可调节的方式系统地控制效率和公平。我们在XChange的基础上评估 R e B u d g e t ReBudget ReBudget,使用运行各种应用程序的多核架构的详细仿真。我们的结果表明, R e B u d g e t ReBudget ReBudget是高效有用的。特别地,可以达到95%的最大可行效率。此外,当结合使用MUR和MBR指标进行分析时,它可以提供最坏情况下的公平性保证
2、市场框架
在决策中,决策者的个性、才智、胆识、经验等主观因素,使不同的决策者对相同的益损问题(获取收益或避免损失)作出不同的反应;即使是同一决策者,由于时间和条件等客观因素不同,对相同的益损问题也会有不同的反应。决策者这种对于益损问题的独特感受和取舍,称之为“效用”。效用曲线就是用来反映决策后果的益损值对决策者的效用(即益损值与效用值)之间的关系曲线。通常以益损值为横坐标,以效用值为纵坐标,把决策者对风险态度的变化在此坐标系中描点而拟合成一条曲线。
假设有N个参与者,M个资源
当被参与者i被分配到资源 r i = ( r i 1 , r i 2 , . . . , r i M ) \pmb r_i=(r_{i1},r_{i2},...,r_{iM}) rri=(ri1,ri2,...,riM),有一个效用函数 U i ( r i ) U_i(r_i) Ui(ri)
效用函数是凹的、非递减的和连续的。
参与者i允许使用 b i j b_{ij} bij去竞标资源 j j j,而且他的竞标花费总和不能超过预算 B i B_i Bi,即
∑ j b i j ≤ B i \sum_j b_{ij}\le B_i j∑bij≤Bi
市场通过采用比例分配方案来协调这些竞标,这种方案被广泛使用,并被认为是公平的。
市场首先收集所有参与者的出价,然后确定每个资源j的价格 p j p_j pj如下:
p j = ∑ i = 1 N B i j C j p_j=\frac{\sum_{i=1}^N B_{ij}}{C_j} pj=Cj∑i=1NBij
C j C_j Cj:资源j的所有数量
参与者 i i i根据其出价按比例获得资源 j j j的 r i j r_{ij} rij个资源单位:
r i j = b i j p j r_{ij}=\frac{b_{ij}}{p_j} rij=pjbij
这种基于市场的方法的本质是,它是一种很大程度上的分布式机制:参与者独立地遍历他们的本地搜索空间,以找到使他们自己的效用最大化的报价,将市场带向帕累托最优的资源配置
为了找到一个最优化竞标,每一个参与者需要解决一个最优化问题,建模如下:
市场公布了资源 j j j的价格 p j p_j pj,参与者能够计算其他参与者对该资源的出价总和:
y i j = ∑ i ′ ≠ i b i ′ j = p j × C j − b i j y_{ij}=\sum_{i'\not=i}b_{i'j}=p_j\times C_j-b_{ij} yij=i′=i∑bi′j=pj×Cj−bij
简化:其他参与者不改变他们的出价,参与者 i i i可以预测当他将出价改变为 b i j ′ b'_{ij} bij′时能获得的资源量 r i j r_{ij} rij
r i j = b i j ′ b i j ′ + y i j C j r_{ij}=\frac{b_{ij}'}{b_{ij}'+y_{ij}}C_j rij=bij′+yijbij′Cj
将公式(5)与参与者 i i i的效用函数 U i ( r i ) U_i(\pmb r_i) Ui(rri)结合,参与者可以根据其出价获得其效用函数
U i ( b i ) = U i ( b i j b i j + y i j C j ) U_i(\pmb b_i)=U_i(\frac{b_{ij}}{b_{ij}+y_{ij}}C_j) Ui(bbi)=Ui(bij+yijbijCj)
参与者面临的优化问题如下:
max U i ( b i ) s . t . ∑ j b i j ≤ B i \max U_i(\pmb b_i)\\ s.t.\ \sum_{j}b_{ij}\le B_i maxUi(bbi)s.t. j∑bij≤Bi
使用拉格朗日乘子法,可以得到,如果最优出价存在,则存在特定于参与者的常量 λ i > 0 λ_i>0 λi>0,使得对于任何资源
∂ U i ∂ b i j { = λ i i f b i j > 0 < λ i i f b i j = 0 \frac{\partial U_i}{\partial b_{ij}}\begin{cases} =\lambda_i&if\quad b_{ij}>0\\ <\lambda_i&if\quad b_ij=0 \end{cases} ∂bij∂Ui{=λi<λiifbij>0ifbij=0
直观地,我们将 λ i j λ_{ij} λij定义为:参与者 i i i将其对资源 j j j的出价改变一个单位时的效用变化率(边际效用):
λ i j = ∂ U i ∂ b i j λ_{ij}=\frac{∂U_i}{∂b_{ij}} λij=∂bij∂Ui
根据公式8,如果参与者 i i i对不同的资源 j j j提交非零的出价,则所有这些资源的 λ i j λ_{ij} λij相同,并且等于公式8中的 λ i λ_i λi。对于零出价的资源,其 λ i j λ_{ij} λij必然小于 λ i λ_i λi。
❗️举例说明
假设参与者 i i i竞标两个资源, λ i 1 = 1 , λ i 2 = 2 λ_{i1}=1,λ_{i2}=2 λi1=1,λi2=2。如果参与者将一个竞价单位从资源1移动到资源2,则其效用可以增加1个单位(资源1的效用为-1,资源2的效用为+2)。因此,当前的出价并不是最优的,参与者可以通过调整出价来不断提高其效用,直到 λ i j λ_{ij} λij相等,或者对其中一个资源的出价降至零
2.1 市场均衡
市场均衡状态是指所有参与者都没有动力改变出价来提高效用,资源价格保持稳定。这是一个令人满意的状态,因为它被证明是帕累托最优的(也就是说,没有任何其他资源分配可以使任何一个个体在不使至少一个个体的更差的情况下变得更好)。为了找到一个市场均衡,我们采用了一个基于迭代式的出价过程算法,类似于我们最近在XChange工作中使用的过程。
基于迭代式的出价过程算法
1️⃣市场广播当前资源的价格给所有的参与者
2️⃣参与者调整他们的出价以最大化自己的效用值
以上两个步骤不断重复,直到两次迭代的浮动小于1%
在一个竞争激烈的市场中,市场均衡总是存在的,对于任何资源 j j j,总是存在至少两个参与者进行非零出价。
引理1:在竞争激烈的市场中,均衡总是存在的。这种市场均衡可能不是唯一的。
2.2效率
鉴于市场均衡的存在,其系统效率,也被称为social welfare,是一个重要的衡量标准。
定义1:系统的效率被定义为参与者的效用之和:
E f f i c i e n c y = ∑ i U i ( r i ) Efficiency=\sum_iU_i(\pmb r_i) Efficiency=i∑Ui(rri)
Nissan等人表明市场均衡的效率可以很低。Papadimitriou引入了无政府状态价格(PoA)的概念,它是相对于最优配置效率,是市场均衡的下界
PoA——纳什均衡/社会最优:
当参与博弈的每个决策者都基于对方决策,做出了自己的最优决策时,这个博弈中所有参与者,不会再改变自己的行为,我们称这种情形为纳什均衡
数学上,让 r i ∗ \pmb r^*_i rri∗表示最大化系统效率的可行资源分配, Ω Ω Ω是市场均衡中的资源配置集(市场均衡可能不是唯一的),并且 r n ∈ Ω \pmb r^n∈Ω rrn∈Ω是市场均衡结果。
同时定义最大效率:
O P T = ∑ i U i ( r i ∗ ) OPT=\sum_iU_i(\pmb r_i^*) OPT=i∑Ui(rri∗)
市场均衡效率:
N a s h ( r n ) = ∑ i U i ( r i n ) Nash(\pmb r^n)=\sum_iU_i(\pmb r_i^n) Nash(rrn)=i∑Ui(rrin)
PoA的定义如下:
定义 2 : P o A = min r n ∈ Ω N a s h ( r n ) O P T 定义2:PoA=\min _{r^n\in Ω}\frac{Nash(r^n)}{OPT} 定义2:PoA=rn∈ΩminOPTNash(rn)
请注意,PoA是一个下界,这意味着任何市场均衡 r n \pmb r^n rrn的效率都保证大于 P o A × O P T PoA×OPT PoA×OPT。
Zhang研究了具有比例平衡预算的市场中的PoA,其中一个参与者被给予与其最大效用成比例的预算,如拥有所有资源时的效用。Zhang表示:
引理2:具有比例平衡预算的市场均衡具有纳什均衡 P o A = Θ ( 1 N ) PoA=\Theta(\frac{1}{\sqrt{N}}) PoA=Θ(N1)
引理2告诉我们,PoA会随着参与者数量的增加而恶化,因此在大型市场中它可能十分的低
2.3 公平性
Envy-freeness(EF)被广泛用于评估现实生活中资源分配的公平性,它最近由Zahedi和Lee在CMP中的资源分配背景下引入。
引理3:一个分配 r = ( r 1 , . . . , r N ) \pmb r=(r_1,...,r_N) rr=(r1,...,rN)的Envy-freeness(EF):
E F ( r ) = min i , j U i ( r i ) U i ( r j ) EF(\pmb r)=\min_{i,j}\frac{U_i(\pmb r_i)}{U_i(\pmb r_j)} EF(rr)=i,jminUi(rrj)Ui(rri)
根据定义,当EF≥1时,资源分配是envy-free的——即参与者更喜欢自己的资源而不是其他人的资源(在最坏的情况下,他们同样喜欢它们)。尽管市场均衡在某种形式的效用约束下被证明是envy-free的,但总的来说并非如此。尽管市场均衡看起来通常是公平的(只要每个参与者都拥有相同的预算)但Zhang表明这并不能保证。Zhang将c-approximate envy-free(c≤1)定义如下:
定义4:如果任何市场均衡的envy-freeness大于c,即对于任何参与者 i i i, U i ( r i ) ≥ c ⋅ max j U i ( r j ) U_i(r_i)≥c·\max_jU_i(\pmb r_j) Ui(ri)≥c⋅maxjUi(rrj),则市场是 c − a p p r o x i m a t e e n v y − f r e e c-approximate\ envy-free c−approximate envy−free。
需要注意的是,Zhang证明的效率和公平界限可能不会同时适用。回想一下,引理2需要按比例平衡的预算分配(即参与者的budget与其可实现的最大效用成正比),而引理3假设每个参与者都有相同的预算。但请注意,在我们研究的多核资源分配问题中,效用函数实际上是一个归一化为最大效用的值。
因此,所有参与者的最大效用为1,因此这两个市场在本文的范围内是等价的。
所以,通过在我们的上下文中结合引理2和引理3,我们发现尽管对所有参与者具有相同预算的市场具有良好的公平性保证,但其效率可能很低(最坏情况下为最优分配的 1 / N 1/\sqrt{N} 1/N)。在以下部分中,我们将研究跨参与者的预算分配如何影响效率和公平的理论界限,以及如何利用该理论设计预算重新分配方案以系统地权衡效率和公平。
3、理论结果
在本节中,我们将介绍两个将服务于我们目标的新指标:市场效用范围(MUR)和市场预算范围(MBR)。通过衡量市场均衡中的MUR和MBR,我们可以定量地了解效率和公平损失的界限。此外,MUR和MBR也可以作为调整跨参与者预算的指导,以便我们更有效地在效率和公平之间做出权衡。
3.1效率
根据公式6,在一个预算受到限制的市场中,如果参与者 i i i以最优方式出价以最大化其效用,则其出价的边际效用 ∂ U i ∂ b i j \frac{\partial U_i}{\partial b_{ij}} ∂bij∂Ui是特定常量 λ i λ_i λi,这对于具有非零出价的所有资源 j j j是相同的。我们的直觉是,参与者之间的 λ i \lambda_i λi变化越大,通过重新分配预算来提高系统效率的“潜力”就越大,因此当前市场的PoA效率保证就越低。
考虑如下的例子:
1️⃣假设一个有两个参与者(A和B)的预算受限市场,使得 λ A = 1 λ_A=1 λA=1和 λ B = 3 λ_B=3 λB=3处于均衡状态。直观的是,如果市场将1个单位的预算从A移动到B,则平衡效率(即A和B的效用之和)可能会增加(增加2个单位,A增加-1,B增加+3)
2️⃣相反,考虑 λ A = 1 λ_A=1 λA=1和 λ B = 2 λ_B=2 λB=2。在这种情况下,相同的预算重新分配也指向市场效率的提高,但改进可能低于第一种情况。
3️⃣最后,考虑 λ A λ_A λA和 λ B λ_B λB相等。在这种情况下,重新分配预算不会对整体市场效率产生影响。
定义市场效用范围(MUR)如下:
定义5:最大效用范围是市场参与者边际效用 λ i λ_i λi的最大变化, M U R = min i λ i max i λ i MUR=\frac{\min_iλ_i}{\max_iλ_i} MUR=maxiλiminiλi通过使用这样的定义,我们可以证明:
定理1:如果 M U R ≥ 0.5 MUR\ge0.5 MUR≥0.5,市场均衡的 P o A ≥ ( 1 − 1 4 M U R ) ≥ 0.5 PoA\ge(1-\frac{1}{4MUR})\ge0.5 PoA≥(1−4MUR1)≥0.5,即保证整体市场效率至少为最优配置的50%;如果 M U R < 0.5 , P o A ≥ M U R MUR<0.5,PoA≥MUR MUR<0.5,PoA≥MUR
MUR不仅提供了整体市场效率的下限,还可以用于指导预算重新分配,以帮助提高整体市场效率。如上例所示,通过将部分预算从 λ i λ_i λi较低的参与者 i i i转移到另一个 λ i ′ λ_i' λi′较高的参与者 i ′ i' i′,MUR向1移动,因此,PoA保证增加,实际市场效率有望增加。
可以证明,参与者 i i i的出价边际效用 λ i λ_i λi随着预算的增加而单调递减。
3.2 Envy-freeness
将不同预算分配给不同参与者的一个可能的副作用是,它可能会对公平性产生负面影响。显而易见,预算最高的参与者能够购买的资源比其他人多,因此很可能会被其他人“嫉妒”。因此,我们假设均衡市场的嫉妒(或无嫉妒)的一个有价值的指标是参与者之间预算的变化:
定义6:市场预算范围是参与者之间预算的最大变化, M B R = min i B i max i B i MBR=\frac{\min_iB_i}{\max_iB_i} MBR=maxiBiminiBi
值得注意的是,MBR定义为最小预算除以最大预算,因此较大的预算变化意味着较低的MBR值。基于这个定义,我们可以证明:
定理2:具有预算范围MBR的市场均衡是( 2 1 + M B R − 2 2\sqrt{1+MBR}-2 21+MBR−2)-近似无嫉妒
这里的关键见解是,通过结合定理1和定理2,我们可以尝试调整效率和公平之间的权衡:如上图所示,重新分配预算以使MUR越更接近1,我们可以实现的系统效率越高。但是,它会导致参与者预算的更大差异,这反过来可能会损害公平性。
值得注意的是,此类预算重新分配并不能保证效率或不嫉妒的实际改善。尽管如此,我们的期望是,根据我们的MUR和MBR定理,通过收紧效率/无嫉妒的界限,最终的均衡分配将倾向于朝着期望的方向移动。因此,我们设想一种算法,通过结合使用MUR和MBR,可以尝试微调市场在效率和公平之间的权衡。我们提出的这种算法命名为:ReBudget。
4、ReBudget框架
在本节中,我们首先描述基于市场的资源配置的基本框架:ReBudget,这是一种基于第3节中的理论结果的实用启发式方法,用于在参与者之间分配预算,从而可以实现系统效率和公平性之间的可调整权衡。
4.1基于市场的方法
我们在第2节中描述的基于市场的基本资源分配框架是一个动态的比例市场。在这个框架中,目标是使用迭代的投标定价步骤找到市场均衡,然后资源按比例分配给投标。该机制在第2.1节中有详细说明。
共享缓存空间和片上功率中最常针对的两个资源,我们对ReBudget的评估将集中在这两个资源上。我们的机制是一个通用框架:只要资源的效用函数可以准确建模,并且该效用函数是非递减的、连续的、凹的(或可以转变为凹的),那么本文的结果就可以应用。(请注意,先前的研究表明,缓存的效用函数通常是不连续的:例如,如果按缓存方式分区——并且是非凹的,这与我们的理论不一致。我们稍后会在第4.1.1节中描述如何解决此类问题。
在任何时间点,我们保证每个核都将获得最低数量的资源:一个缓存区域(128kB),以及以最低频率运行的功率(我们的设置中为800MHz)。剩余的缓存容量和功率预算使用基于市场的机制进行分配。这是为了保证每个应用程序至少能够运行,而不管其购买力如何。
我们现在解决设计市场的两个主要挑战:如何模拟参与者的效用,以及参与者如何竞标以最大化他们的效用。
4.1.1 效用函数
在我们研究的多核资源分配问题中,我们将应用程序的效用定义为它的IPC,并归一化为当它单独运行(因此拥有所有资源)时的IPC:
U i ( r i ) = I P C ( r i ) / I P C a l o n e U_i(\pmb r_i) =IPC(\pmb r_i)/IPC_{alone} Ui(rri)=IPC(rri)/IPCalone
所以, U i U_i Ui的值就在0和1之间
IPC是每周期指令的缩写,它衡量的是一个CPU在一个时钟周期内可以执行多少条指令。
为了弄清楚效用函数的性能-资源关系,我们采用了我们最近的XChange工作的监测技术:我们将应用程序的总执行时间划分为计算和存储阶段。使用UMON shadow tags和关键路径预测器估计不同缓存分配下的存储阶段长度。使用Isci等人开发的功率模型估计算阶段的长度和相应的功耗。两个阶段的总和是给定缓存功率的执行时间估计。这都是在线动态建模的,不需要任何事先的离线分析
在第2节中,为了应用理论结果,要求参与者的效用函数是凹的、连续的且非递减的。然而,在计算机体系结构中,这并不总是正确的。一方面,功率是凹的,并且细粒度到足以将其视为连续的。另一方面,众所周知,缓存容量是一种非凹的、非连续的资源
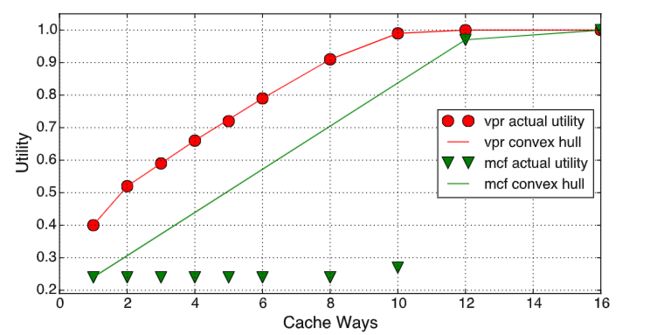
上图显示了两个代表性应用程序mcf和vpr的缓存效用。这些标记是每个应用程序在被赋予不同的缓存路径(功率预算不变)时的效用(归一化IPC)。从图中,我们可以观察到两点
首先,这样的效用函数不是连续的,因为它是由相对粗粒度的cache way划分的。为了使其连续,我们采用了Wang和Chen的无用伸缩,这是一种反馈控制机制,可以精确地将分区大小保持在cache lines的粒度接近目标。我们根据经验将分配粒度设置为128kB,我们将其称为cache region
其次,缓存效用可能不是凹形的。尽管vpr展示出了凹效用函数,但mcf显然不是:对于1到10个cachelines,它的归一化效用持平于0.2,一旦它确保了12路(1.5Mb),则突然增加到1.0。这是因为mcf的工作集大小是1.5MB,并且12个或更多的cache lines将通过将L2 cache未命中率降低到几乎为零来满足其需要。为了解决这个问题,我们应用了Talus,一种凸化缓存行为的技术。
Talus的工作原理大致如下:首先,基于应用程序的实际缓存效用,推导出效用的“凸壳”,即缓存效用的凸集。壳上的缓存分配点被称为“信息点”(PoI),这是所需的分配。接下来,为了使缓存效用在凸壳上保持连续,Talus将一个核的缓存分区划分为两个“影子”分区。在给定任意缓存分区目标的情况下,Talus首先找到它的两个相邻PoI,然后相应地调整影子分区的大小。访问流也相应地被划分为两个影子分区。更多细节可以在Talus中找到。如图2所示,Talus有效地将缓存行为凸化为凸壳,满足凹性和非减性的要求
4.1.2 投标策略
既然我们已经为每个参与者构建了一个效用函数,根据市场的投标定价程序步骤,下一个问题是每个参与者如何找到其最优出价以实现其效用最大化。因为缓存和功率效用都是凹的,所以像hill-climbing这样的启发式方法在寻找最优解时是合适的。因此,我们采用如下一种简单的hill-climbing技术
Hill climbing 是在数值分析中一个用于获得局域最优解的算法工具。Hill climbing 本质上是一种迭代算法,即对于某个问题先给出一个随机的答案,然后不断搜索局域空间的其它解并以增量的方式加到初始解上,如果该增量使得答案更优则保留并继续添加下一个增量,反之则摒弃该增量并继续添加下一个增量,如此反复迭代,直到找不到使当前解更优的增量,最后得到的答案便是所需要的局域最优解。它的一个重要优势是,无论在计算中的任何时间被中断,它都能返还当前的最优解。
1️⃣每个参与者 i i i将其预算 B i B_i Bi根据 j j j份资源等额分成出价 b i j b_{ij} bij。另外,参与者在不同资源之间转移预算的金额 S S S,将是竞标金额的一半。
2️⃣每个参与者 i i i计算所有资源 j j j的边际效用 λ i j λ_{ij} λij。根据方程8的最优条件,如果参与人的出价使其效用最大化,那么所有收到非零出价的资源的边际效用必然是相同的——换句话说,参与者没有动机在资源之间重新分配其预算。否则,如果在当前的投标条件下,不同的资源的 λ i j λ_{ij} λij不同,参与者就会从 λ i k λ_{ik} λik较低的资源 k k k转移到另一个 λ i k λ_{ik} λik较高的资源 k ′ k' k′,这样的移动会使这两种资源的边际效用趋于均衡(记住,参与者的效用函数是凹的,这意味着随着投标 b i j bij bij的增加,边际效用 λ i j λij λij会减小)。
3️⃣将S减半,重复此过程,直到满足以下两个条件之一
️任一资源的 λ i j λ_{ij} λij保持不变(差异在5%以内)
️S小于总预算的1%。由于S随每一步呈指数衰减,且 λ i j λij λij是单调的,因此该算法可以快速达到对资源的最优报价。
预算重分配算法
到目前为止讨论的机制适用于一般预算受限的市场机制中的个体参与者。在本节中,我们将描述ReBudget,这是一种在上述机制之上工作的启发式方法。ReBudget将不同的预算以可调整的方式分配给参与者,从而在系统效率和公平性之间进行权衡。
正如第3节所讨论的,MUR和MBR是表明多核效率和公平性的良好指标。利用MUR,我们可以识别系统效率的下界,如定理1所示。此外,由于效用的凹性,当参与人 i i i的预算 B i B_i Bi降低时,其 λ i λ_i λi增加。因此,通过减少具有较低 λ i λ_i λi的参与者的预算,系统MUR,即市场参与者的边际效用 λ i λ_i λi的最大变化,将接近1,可能产生更高的效率。然而,另一方面,通过在参与者之间创造更大的预算变化,MBR将会减少(回想3.2节,更大的预算变化将会减少MBR),因此也会降低公平水平(即envy-freness)。
在ReBudget中,我们试图在保证一定程度的公平的同时最大化效率。系统管理员可以设置一个最低可接受的envy-freeness level,使用定理2可以计算出最小的MBR。然后,在市场均衡条件下,根据各参与者的 λ i λ_i λi值对其预算进行重新分配, λ i λ_i λi值较低的参与者预算会减少。如果一个参与者的 λ i λ_i λi小于最大 λ i λ_i λi的50%,我们将其定义为“低 λ i λ_i λi”。在定理1中,我们发现当MUR小于0.5时,PoA开始线性下降。在任何时间点上,参与者之间的预算变化都必须高于设定的MBR值。
我们设计了一种指数回退的迭代方法:
1️⃣MBR是基于管理员设置的最低可接受公平水平来计算的。为了开始对市场的竞标,每个参与者都被分配了相同的预算B。预算重分配的数量,叫做“step”,其值被初始化为 ( 1 − M B R ) ⋅ B 2 (1-MBR)\cdot\frac{B}{2} (1−MBR)⋅2B
2️⃣参与者们然后使用自己的预算来执行4.1.2中的算法来达到市场均衡。
1️⃣每个参与者 i i i将其预算 B i B_i Bi根据 j j j份资源等额分成出价 b i j b_{ij} bij。另外,参与者在不同资源之间转移预算的金额 S S S,将是竞标金额的一半。
2️⃣每个参与者 i i i计算所有资源 j j j的边际效用 λ i j λ_{ij} λij。根据方程8的最优条件,如果参与人的出价使其效用最大化,那么所有收到非零出价的资源的边际效用必然是相同的——换句话说,参与者没有动机在资源之间重新分配其预算。否则,如果在当前的投标条件下,不同的资源的 λ i j λ_{ij} λij不同,参与者就会从 λ i k λ_{ik} λik较低的资源 k k k转移到另一个 λ i k λ_{ik} λik较高的资源 k ′ k' k′,这样的移动会使这两种资源的边际效用趋于均衡(记住,参与者的效用函数是凹的,这意味着随着投标 b i j bij bij的增加,边际效用 λ i j λij λij会减小)。
3️⃣将S减半,重复此过程,直到满足以下两个条件之一
️任一资源的 λ i j λ_{ij} λij保持不变(差异在5%以内)
️S小于总预算的1%。由于S随每一步呈指数衰减,且 λ i j λij λij是单调的,因此该算法可以快速达到对资源的最优报价。
3️⃣ 收集到每个参与者的 λ i \lambda_i λi。如果一位参与者的 λ i \lambda_i λi小于市场中 λ i \lambda_i λi的最大值的50%,它的预算就会减少一“step”。
4️⃣“step”减半,算法跳至2️⃣来重新找到一个市场均衡。
当“step”的值小于每个参与者初始预算的1%或者当没有参与者的预算被减少时,产生的市场均衡值就是最终的结果。
上述算法有两个优点:
1️⃣任何参与者的最高预算是B,最低预算是 M B R ⋅ B MBR\cdot B MBR⋅B(如果参与者在所有迭代中预算都减少)。因此,参与者预算的最大波动范围在MBR范围之内,从而保证设计者设置的fairness level。
2️⃣“step”的指数减少保证了这些步骤是快速的。所以市场仍然是高效的,可扩展的,有能力去处理大规模系统。
上述的指数回退贪心算法展示了如何使用MUR和MBR指导预算重新分配,以此来优化系统。正如我们将在第6节中展示的,这样的算法在实践中实际上是快速有效的
4.3 实现
我们现在讨论ReBudget算法的硬件与软件实现。在硬件方面,ReBudget需要:
1️⃣ 硬件监管器用于对应用程序的效用-资源关系进行建模。正如在4.1.1节中讨论的,我们采用了我们在XChange中使用的硬件监管器。因此,每个核的开销为3.7kB,监视器的总开销不到总缓存的1%
2️⃣ 每个分区和每个缓存行的额外状态用于将缓存进行分区。我们采用Futility Scaling(一种高结合性的缓存分区方法)对L2 cache进行分区。它会产生占总缓存1.5%的存储开销
在软件方面,为了处理由于上下文切换和应用程序阶段变更而导致的资源需求变化,每1毫秒触发4.2节中描述的预算重新分配算法来重新分配资源。与XChange类似,这样的算法可以被负载到Linux核心的APIC计时器(高级可编程中断控制器)中断中,并且运行时开销很低
5、实验方法
5.1模型架构
我们使用SESC,一个非常详细的执行驱动模拟器——经过内部修改以适应实验设置,来评估我们的ReBudget算法。我们建立了四路无序核心,表格1展示了CMP中最重要的一些参数。
有序(InO)核心由于其低复杂度和高能效而被广泛使用,但性能有限。 这是因为InO调度的性质导致错过了利用指令级并行性(instruction-level parallelism,ILP)和内存级并行性(memory-level parallelism,MLP)的机会。 无序(OoO)核心通过动态构造所有运行中指令的数据依赖关系图并根据源操作数和执行资源的可用性对其进行重新排序,从而克服了这些限制。 为了支持OoO调度,当今的处理器配备了唤醒/选择和内存消除歧义方案。 众所周知,这些方案占了OoO核心功耗的很大一部分,因为发布队列(issue queue, IQ)和加载/存储单元(load/store unit, LSU)由大量多端口内容可寻址存储器(content addressable memories, CAM) 和随机存取存储器 (random access memories, RAM)组成,并由每个指令多次访问。

我们还准确地模拟了Micron的DDR3-1600 DRAM时序
我们使用Watch(架构级功率分析和优化的框架)和Cacti(一个集成的缓存定时、功率和区域模型)来模拟处理器和内存系统的动态功耗。我们采用英特尔的Sandy Bridge电源管理方法将静态功耗近似为动态功耗的一小部分,动态功耗呈指数依赖于系统温度。使用与SESC集成的Hotspot估计多核芯片的运行时温度。
我们的多核芯片能够调节两个共享片上资源:功耗预算以及共享的最后一级缓存。功耗预算通过每核DVFS进行调节,类似于英特尔的RAPL技术。只要整体功率消耗保持在 p × 10 p\times10 p×10W( p p p是处理器核心的数量),每个核心可以以800MHz到4GHz之间的频率运行。最后一级(L2)缓存使用Wang和Chen的Futility Scaling进行分区,粒度为128kB(一个缓存区域)。二级缓存总容量为 p × 512 k B p×512kB p×512kB。由于存在UMON shadow tag的开销,我们将其堆栈距离限制为16,即shadow tag可以估计容量从128kB到2MB的缓存的未命中率。
DVFS 即动态电压频率调整,动态技术则是根据芯片所运行的应用程序对计算能力的不同需要,动态调节芯片的运行频率和电压(对于同一芯片,频率越高,需要的电压也越高),从而达到节能的目的。
RAPL:运行平均功率限制”(Running Average Power Limit)
我们凭经验观察到,我们的应用程序中很少有超过2MB的缓存区域受益,即使这样,鉴于每个参与者的预算有限,如此大的缓存区域通常是负担不起的。在32的动态采样率下,影子标签每个核心占用3.6kB,不到L2缓存大小的1%。
我们保证每个核心都至少有一个缓存区域,以及足够的功率预算,使其能够以最低频率(800MHz)运行。剩余资源将根据基于市场的资源分配决策进行完全分配(即没有剩余)。
工作负荷构建
我们混合使用来自SPEC2000和SPEC2006的24个应用程序来评估我们的提案。每个应用程序都使用gcc 4.6.1通过-O2优化交叉编译到MIPS ISA(经典RISC指令集)。对于所有模拟,我们使用Simpoints来挑选每个应用程序中最具代表性的2亿条动态指令块。
SPEC CPU2000是由标准性能评价机构“The Standard Performance Evaluation Corporation (SPEC)”开发的用于评测CPU性能的基准程序测试组。处理器、内存和编译器都会影响最终的测试结果,而I/O(磁盘)、网络、操作系统和图形子系统对SPEC CPU2000的影响非常小。目前,SPEC CPU2000是业界首选的CPU评测工具。 SPEC CPU2000包括CINT2000和CFP2000两套基准测试程序,前者用于测量和对比CPU的定点性能,后者用于测量和对比浮点性能。CINT2000包含12个测试项目,CFP2000包含14个测试项目。
Benchmarks:用高级语言定义的一组程序,在一个特定的应用程序或系统编程领域中,尝试提供一个计算机的代表性测试
特征:用高级语言编写,使其可移植到不同的机器;代表一种特殊编程风格,如系统编程、数字编程或商业编程;测量容易;分布广泛
Simpoint:基于检查点的采样
我们的评估基于多道程序工作负荷,因为我们预计会以核心为粒度分配资源。对于多线程工作负荷,如果每个线程运行在不同的核心上,我们仍然可以按线程粒度分配资源。另一种选择是按应用程序粒度分配资源。一个应用程序的所有线程可能共享相同的资源,这是一个合理的假设,因为在许多编程模型中,并行应用程序的线程之间的需求往往是相似的。
为了构建我们的多道程序工作负载,我们根据分析将24个应用程序分为四类:
缓存敏感©、功率敏感§、两者敏感(B)和无(N)。
然后,我们创建了六类多道程序工作负载:CPBN、CCPP、CPBB、BBNN、BBPN和BBCN。对于每个类别,我们为8核和64核配置随机产生40个工作负载。随机生成的工作原理如下:对于8核(64核)配置,从每个应用程序类中随机选择2(16)个应用程序
例如,CPBN表示C、P、B、N中的每个有2(16)个应用程序,而CCPP在C中将有4(32)个应用程序,在P中将有4(32)个应用程序
性能指标
资源分配中的一个关键问题是指标值。正如第4.1节所讨论的,我们将应用程序的效用定义为当它单独运行时归一化后的IPC: U i ( r i ) = I P C ( r i ) / I P C a l o n e U_i(\pmb r_i)=IPC(\pmb r_i)/IPC_{alone} Ui(rri)=IPC(rri)/IPCalone。系统效率可以计算如下:
Efficiency = ∑ i = 1 N U i = ∑ i = 1 N IPC i ( r i ) IPC i a l o n e \text{Efficiency}=\sum_{i=1}^NU_i=\sum_{i=1}^N\frac{\text{IPC}_i(r_i)}{\text{IPC}_i^{alone}} Efficiency=i=1∑NUi=i=1∑NIPCialoneIPCi(ri)
IPC是每周期指令的缩写,它衡量的是一个CPU在一个时钟周期内可以执行多少条指令。
我们意识到这正是加权加速,衡量系统吞吐量的常用指标,并已被广泛接受。因此,我们的PoA研究在计算机体系结构中变得有意义:它保证了市场均衡中吞吐量的下限。
一个系统可以通过饥饿一个或两个应用程序同时使所有其他应用程序受益来实现高吞吐量(即加权加速);但是,系统公平性会因此受到影响,给一些用户带来不好的体验。因此,我们使用envy-freeness来评估公平性,这是经济学中广泛使用的指标,最近由Zahedi和Lee引入,用于评估多核芯片的公平性。
6、评估
我们分两个阶段评估我们的proposal。
1️⃣ 在第一阶段,我们通过假设应用程序的效用函数可以完美地建模和凸化来分析研究ReBudget的有效性。仅在这个阶段,我们使用我们的模拟基础设施广泛地分析每个应用程序。(回想一下,ReBudget不需要离线分析;我们的第二阶段使用硬件监视器在运行时模拟效用函数,如第4.1.1节所述。)
我们对90个缓存+功率配置点进行采样,具有{1-6、8、10、12、16}个缓存区域(10个可能的分配)和{0.8,1.2,1.6,…,4.0}GHz(9个可能的分配)。对于每个点,我们收集平均IPC和功耗。然后,我们推导出缓存和功耗的凸包,并假设它们的效用是完全凹的和连续的。最后,我们通过将ReBudget和其他竞争机制应用于所有240个软件集来分析评估系统效率和公平性。
2️⃣ 在第二阶段,我们在模拟 CMP 环境 (SESC) 中评估 ReBudget。应用程序的效用在运行时使用第 4.1.1 节中描述的技术进行监控。我们应用 Talus 和 Futility Scaling来使缓存行为凹化和连续。由于实际模拟时间限制,我们随机选择每个类别的一个应用程序软件集,并使用详细的模拟来运行它。我们使用这些结果来验证我们的第一阶段的评估结果。
我们在 8 核和 64 核 CMP 配置上进行了所有实验,发现结果都是相似的。因此,我们忽略了 8 核配置的结果,重点关注大规模 64 核配置
评估的分配机制如下:
E q u a l S h a r e EqualShare EqualShare:资源在所有处理器核心之间平均分配。
两种 XChange 机制:
1️⃣ E q u a l B u d g e t Equal Budget EqualBudget:资源使用基于市场的程序进行分配,假设所有参与者的预算相同;
2️⃣ $ Balanced$:每个参与者收到与效用成正比的预算,最大(2 MB L2 缓存和 4.0 GHz 频率)和最小(128 kB 和 800 MHz),归一化为前者。
R e B u d g e t − s t e p ReBudget-step ReBudget−step,其中资源使用我们的 R e B u d g e t ReBudget ReBudget机制进行分配,这样在第一次迭代结束时(所有参与者以相同的预算运行),每个参与者都被分配其原始预算或更少的“step”。 (回想一下,在随后的每次迭代中,"step"都会减半。)所有参与者的初始预算都设置为 100。
M a x E f f i c i e n c y MaxEfficiency MaxEfficiency:最大化系统效率的资源分配,是通过运行不可解的非常细粒度的hill-climbing获得的(回想一下,所有效用都是凹的)
6.1 效率
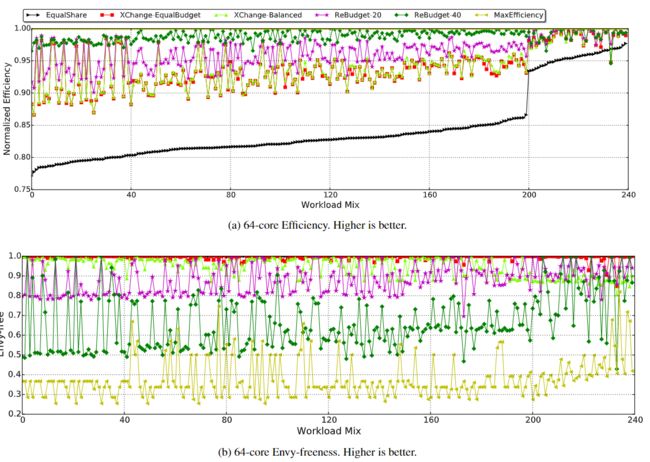
对于第一阶段评估,下图报告了 E q u a l S h a r e EqualShare EqualShare、 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency 以及 X C h a n g e XChange XChange 的 $EqualBudget $和 B a l a n c e d Balanced Balanced 以及具有不同“step”的 R e B u d g e t ReBudget ReBudget 的效率和无嫉妒性。软件集按$ EqualShare $的效率排序。
我们观察到,与 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency相比, E q u a l S h a r e EqualShare EqualShare 的效率在最后 40 个软件集中突然增加。这些软件集中的大多数都属于 B B P N BBPN BBPN类别。 E q u a l S h a r e EqualShare EqualShare非常适合 B B P N BBPN BBPN工作负载,因为软件集中 75% 的应用程序是功率敏感型的,在 E q u a l S h a r e EqualShare EqualShare 中平均分配功率的效果非常好。此外,虽然可以通过为“B”应用程序提供更多缓存来提高效率,但它们不像“C”应用程序那样对缓存敏感。因此,缓存中的 E q u a l S h a r e EqualShare EqualShare对于 B B P N BBPN BBPN软件集的表现优于如 C P B N CPBN CPBN等其他软件集。
6.1.1 EqualBudget vs. EqualShare
我们首先比较了基于市场的 E q u a l B u d g e EqualBudge EqualBudget 机制与 E q u a l S h a r e EqualShare EqualShare分配的效率。图中a显示,在 64 核配置中, E q u a l B u d g e t EqualBudget EqualBudget中 37% 的工作负载能够实现 $MaxEfficiency 的 95 的 95% 的welfare,而且 的95EqualBudget$中超过 90% 的软件集在 90% 以内。这证明了基于市场的机制在此设置中是稳健、高效和可扩展的。
但是,仍然有10%的应用程序低于最优分配下welfare的90%。我们观察到,超过一半的工作负载属于 BBPC 类别,其中支持两种资源的应用程序数量 (50%) 远高于偏爱功率 (25%) 或缓存 (25%) 的应用程序数量。这让人想起著名的公共资源悲剧。 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency强烈偏爱只偏好一种资源的应用程序,为了更高的系统效率而牺牲需要两种资源的“B”应用程序。 E q u a l B u d g e t EqualBudget EqualBudget机制允许所有应用程序公平地相互竞争,即使代价是效率不如$ MaxEfficiency $的好。
公共资源悲剧:一群牧民面对向他们开放的草地,每一个牧民都想多养一头牛,因为多养一头牛增加的收益大于其购养成本,是合算的,但是因平均草量下降,可能使整个牧区的牛的单位收益下降。每个牧民都可能多增加一头牛,草地将可能被过度放牧,从而不能满足牛的食量,致使所有牧民的牛均饿死。这就是公共资源的悲剧。
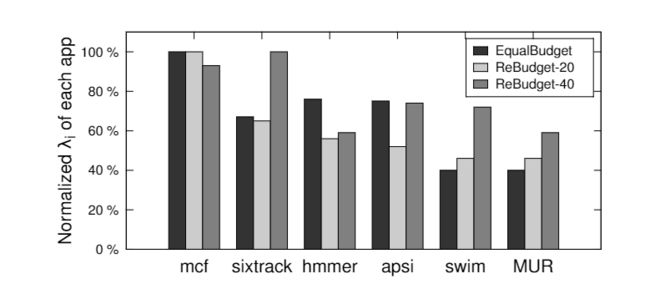
我们仔细研究了一个使用 BBPC 软件集的 8 核实验,该软件集包含四个“B”应用程序( a p s i apsi apsi和 s w i m swim swim,各 2 个副本)、两个“C”应用程序(2 个 mcf 副本)和两个“P”应用程序( h m m e r hmmer hmmer和 s i x t r a c k sixtrack sixtrack)。这种具有 E q u a l B u d g e t EqualBudget EqualBudget 的软件集的整体效率是 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency的 90%,我们发现它的 M U R = 0.40 MUR = 0.40 MUR=0.40。下图显示了市场均衡时每个应用程序的 λ i λ_i λi值。我们可以发现,使用 E q u a l B u d g e t EqualBudget EqualBudget时,“B”应用程序 s w i m swim swim的 λ i λ_i λi 值最低,表明它预算过多,没有有效地使用它的资金;另一方面,“C”应用程序 m c f mcf mcf具有最高的 λ i λ_i λi值,表明预算增加可以导致高效用增益
6.1.2 XChange-Balanced
XChange 的 B a l a n c e d Balanced Balanced预算分配是一种在参与者之间分配预算以提高效率的直观方式。然而,图 4a 表明它在效率上并没有超过 $EqualBudget $太多,而实际上它在公平性上有所损失,如图 4b 所示。原因是:
1️⃣ 除了“N”型应用程序对任何资源都不敏感外,大多数应用程序的最小效用和最大效用之间的性能差异是相似的,尤其是当我们免费为每个参与者分配最小资源时。因此,预算分配与 $EqualShare $没有太大区别。
2️⃣ 盲目地将参与者的预算设置为与他的“potential”成正比,而忽略效用和 MUR 指标的形状,是无效的。
6.1.3 ReBudget
我们评估了第4.2节中提出的 R e B u d g e t ReBudget ReBudget机制。我们通过将每次迭代(即"step")的预算减少量设置为20和40,测试了不同的侵略性。图4a清楚地显示,通过更积极地重新分配预算,所有软件集的效率都将提高。此外,对于所有240个软件集, R e B u d g e t − 40 ReBudget-40 ReBudget−40实现了 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency的95%的系统效率。
我们仔细查看了我们在6.1.1节中学习的8核软件集。对于 R e B u d g e t − 20 ReBudget-20 ReBudget−20, λ i λ_i λi的最低值增加到0.46(在 E q u a l B u d g e t EqualBudget EqualBudget下, λ i λ_i λi在0.40是最低的),因为它的预算从100(每个参与者的初始预算)下降到61.25单位( R e B u d g e t − 20 ReBudget-20 ReBudget−20下的最低预算)。而具有最大 λ i λ_i λi的 m c f mcf mcf,其预算不变(100)。其他应用的预算降低到80左右,因为它们的 λ i λ_i λi值明显低于 m c f mcf mcf。注意, a p s i apsi apsi和 h m m e r hmmer hmmer的 λ i λ_i λi减少了,尽管它们的预算减少了。这是因为 s w i m swim swim预算的削减使得资源价格大幅下降。因此,虽然$apsi $和 h m m e r hmmer hmmer的预算减少了,但它们实际上可以负担更多的资源,它们的 λ i λ_i λi也减少了。总体而言, R e B u d g e t − 20 ReBudget-20 ReBudget−20的MUR增加到46%,而 E q u a l B u d g e t EqualBudget EqualBudget的MUR为40%。相应地, R e B u d g e t − 20 ReBudget-20 ReBudget−20的效率提高到 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency的96%
在 R e B u d g e t − 40 ReBudget-40 ReBudget−40, s w i m swim swim(它的的 λ i λ_i λi在ReBudget-20仍然是最低的)的预算进一步削减到了20。因此,其 λ i λ_i λi值从0.46增加到0.72,如图3所示。在这种情况下, m c f mcf mcf不再是 λ i λ_i λi值最高的: s i x t r a c k sixtrack sixtrack的预算下降到30,它开始要求更多的资金。因此,系统的MUR提高到0.59,效率现在是 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency的99%。
6.2 公平性
我们使用在2.3节中讨论的 e n v y − f r e e n e s s envy-freeness envy−freeness作为衡量公平性的指标。我们首先看一下 E q u a l B u d g e t EqualBudget EqualBudget和 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency之间的公平性比较。正如预期的那样,图4b显示 E q u a l B u d g e t EqualBudget EqualBudget几乎是无嫉妒的,在最坏的情况下,它仍然是 0.93-approximate envy-free。相反, M a x E f f i c i e n c y MaxEfficiency MaxEfficiency是不公平的,它通常是0.35-approximate envy-free。
关于XChange-Balanced机制,大多数工作负载的 e n v y − f r e e n e s s envy-freeness envy−freeness保持在0.9,最坏的情况下是 0.86 − a p p r o x i m a t e e n v y − f r e e 0.86-approximate\ envy-free 0.86−approximate envy−free。它不如 E q u a l B u d g e t EqualBudget EqualBudget,考虑到它微不足道的效率收益,以及在效率和公平之间权衡时无法控制侵占性,我们认为这样的机制是无效的
另一方面,ReBudget的 e n v y − f r e e n e s s envy-freeness envy−freeness与它的侵占性有直接的关系。由图4b可知,ReBudget-20和ReBudget-40的典型 e n v y − f r e e n e s s envy-freeness envy−freeness分别为0.8和0.5,且没有一个软件集违反定理2提供的理论保证(0.53和0.19)。我们注意到理论和现实之间存在差距。这是因为定理2说的是一个理论上的下界,它应该在所有情况下都成立。这样的束缚是紧密的,构建一个市场来达到它并不难。虽然它不会发生在我们使用的应用程序上,但它可能会发生在现实生活中。此外,显而易见,所有软件集的 R e B u d g e t − 20 ReBudget-20 ReBudget−20的 e n v y − f r e e n e s s envy-freeness envy−freeness始终高于 R e B u d g e t − 40 ReBudget-40 ReBudget−40。因此,除了提供理论保证外,MBR还可以作为系统公平性的准确指标。
结合第6.1节的研究结果,我们可以得出结论**,预算调整得越积极,效率就越高,相应地实现的公平性就越低。这很吸引人,因为系统设计师和管理员可以使用"step"作为一个“旋钮”来权衡这两个指标**。
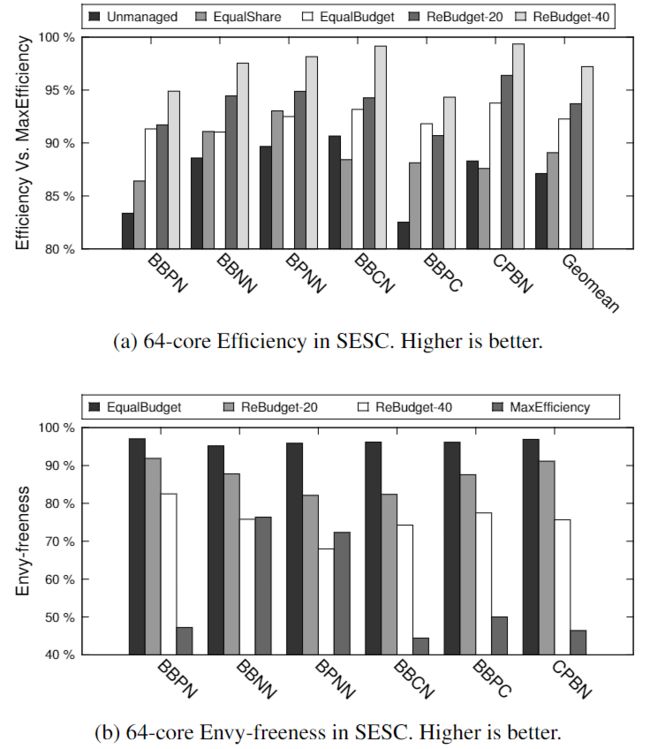
6.3 仿真结果
除了上述分析结果之外,我们还在体系结构模拟器SESC中实现了 R e B u d g e t ReBudget ReBudget。图5显示了两种竞争机制的系统效率和 e n v y − f r e e n e s s envy-freeness envy−freeness。这样的结果与我们上面的分析评价是一致的: R e B u d g e t ReBudget ReBudget相较于 E q u a l B u d g e t EqualBudget EqualBudget,通过牺牲公平来提高系统效率,而且重新分配的预算越积极,效率的提高就越大。相反, E q u a l B u d g e t EqualBudget EqualBudget在无嫉妒性方面达到最高,而以系统效率最大化为目标的 M a x E f f i c i e n c y MaxEfficiency MaxEfficiency在公平性方面最差。 R e B u d g e t ReBudget ReBudget成功地维持了它在这两个极端之间的排名,而侵占性会逐渐损害预期的系统性能
6.4 收敛性
基于市场的机制的一个非常重要的方面就是我们的算法找到均衡分配的速度有多快。就我们所知,收敛时间没有理论上的下界。然而,在现实中,我们发现对于95%的软件包, E q u a l B u d g e t EqualBudget EqualBudget和 X C h a n g e − B a l a n c e d XChange-Balanced XChange−Balanced在3次迭代中收敛。由于预算调整后需要重新收敛,所以重新预算机制需要更多的迭代。然而,预算变化中的指数后退保证了重新预算过程的快速收敛。这些发现与之前的研究一致(例如,Feldman等发现动态市场的收敛时间≤5次迭代)。对于市场无法收敛的极少数情况,我们还采用了故障安全机制:我们简单地在30次迭代后终止均衡查找算法。
7、结论
本文引入了市场效用范围(MUR)和市场预算范围(MBR)两个新指标,分别建立了预算约束下市场均衡的效率损失和公平损失的理论边界。我们提出了 R e b u d g e t Rebudget Rebudget,这是一种预算重新分配的技术,能够以可调节的方式系统地控制效率和公平。我们通过使用运行各种应用程序的多核架构的细致模拟,在先前XChange提议的基础上评估 R e B u d g e t ReBudget ReBudget。我们的结果表明, R e B u d g e t ReBudget ReBudget是$ efficient\ and\ effective$。特别是,当与我们提出的MUR和MBR指标相结合时,重新预算能够有效地在最坏公平约束下最大化效率。