粒子群算法改进——线性递减惯性权重
惯性权重回顾
惯性权重w体现的是粒子继承先前的速度的能力
Shi,Y最先将惯性权重w引入到粒子群算法中,并且分析指出
-
一个较大的惯性权值有利于全局搜索
-
一个较小的权值则更利于局部搜索
线性递减惯性权重
- 在搜索初期，增强全局搜索能力可以更大可能遍历解空间，避免陷入局部最优解 >广撒网
- 在搜索后期，增强局部搜索能力可以更大可能的锁定最优解 >精准打击
为了更好地平衡算法的全局搜索以及局部搜索能力，Shi,Y提出了线性递减惯性权重LDIW(LinearDecreasingInertiaWeight)
公式如下
wd=wstart-(wstart - wend)x (d/K)
d是当前迭代的次数,K是迭代总次数
wstart一般取0.9，wend一般取0.4
与原来的相比，现在惯性权重和迭代次数有关
范例代码
%% 线性递减惯性权重的粒子群算法PSO: 求解函数y = 7*cos(5*x) + 4*sin(x)在[-5,5]内的最大值
clear; clc
%% 绘制函数的图形
x = -5:0.01:5;
y = 7*cos(5*x) + 4*sin(x);
figure(1)
plot(x,y,'b-')
title('y = 7*cos(5*x) + 4*sin(x)')
hold on % 不关闭图形，继续在上面画图
%% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 10; % 粒子数量
narvs = 1; % 变量个数
c1 = 2; % 每个粒子的个体学习因子
c2 = 2; % 每个粒子的社会学习因子
w_start = 0.9; % 初始惯性权重
w_end = 0.4; % 粒子群最大迭代次数时的惯性权重
K = 50; % 迭代的次数
vmax = 1.2; % 粒子的最大速度
x_lb = -3; % x的下界
x_ub = 3; % x的上界
%% 初始化粒子的位置和速度
x = zeros(n,narvs);
x = x_lb + (x_ub-x_lb).*rand(n,narvs) % 随机初始化粒子所在的位置
v = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度
%% 计算适应度
fit = zeros(n,1); % 初始化这n个粒子的适应度全为0
for i = 1:n % 循环整个粒子群，计算每一个粒子的适应度
fit(i) = Obj_fun1(x(i,:)); % 调用Obj_fun1函数来计算适应度
end
pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == max(fit), 1); % 找到适应度最大的那个粒子的下标
gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）
%% 在图上标上这n个粒子的位置用于演示
h = scatter(x,fit,80,'*r'); % scatter是绘制二维散点图的函数
%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度
for d = 1:K % 开始迭代，一共迭代K次
for i = 1:n % 依次更新第i个粒子的速度与位置 **注意这边的变化**
w = w_start - (w_start - w_end) * d / K; % 更新惯性权重
v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度
% 如果粒子的速度超过了最大速度限制，就对其进行调整
for j = 1: narvs
if v(i,j) < -vmax(j)
v(i,j) = -vmax(j);
elseif v(i,j) > vmax(j)
v(i,j) = vmax(j);
end
end
x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
% 如果粒子的位置超出了定义域，就对其进行调整
for j = 1: narvs
if x(i,j) < x_lb(j)
x(i,j) = x_lb(j);
elseif x(i,j) > x_ub(j)
x(i,j) = x_ub(j);
end
end
fit(i) = Obj_fun1(x(i,:)); % 重新计算第i个粒子的适应度
if fit(i) > Obj_fun1(pbest(i,:)) % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
pbest(i,:) = x(i,:); % 更新第i个粒子迄今为止找到的最佳位置
end
if fit(i) > Obj_fun1(gbest) % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
gbest = pbest(i,:); % 更新所有粒子迄今为止找到的最佳位置
end
end
fitnessbest(d) = Obj_fun1(gbest); % 更新第d次迭代得到的最佳的适应度
pause(0.1) % 暂停0.1s
h.XData = x; % 更新散点图句柄的x轴的数据
h.YData = fit; % 更新散点图句柄的y轴的数据
end
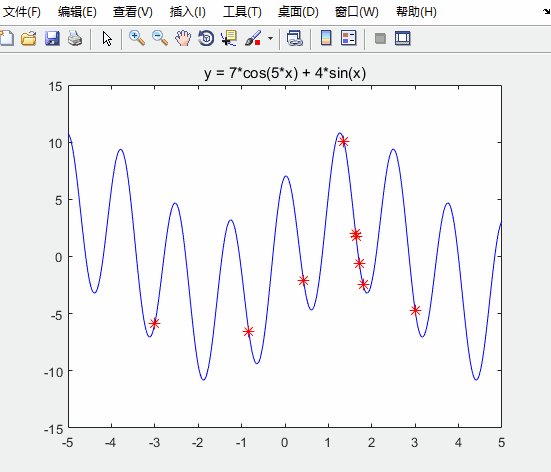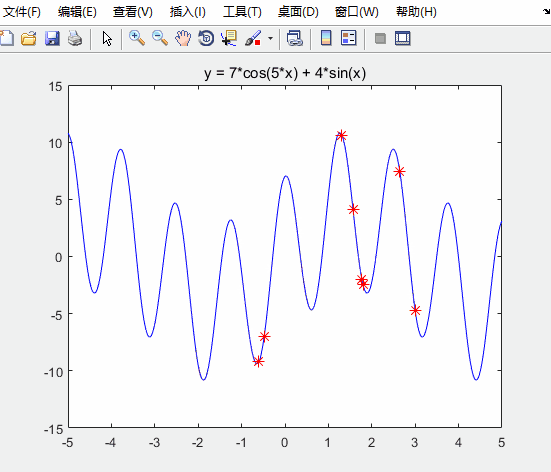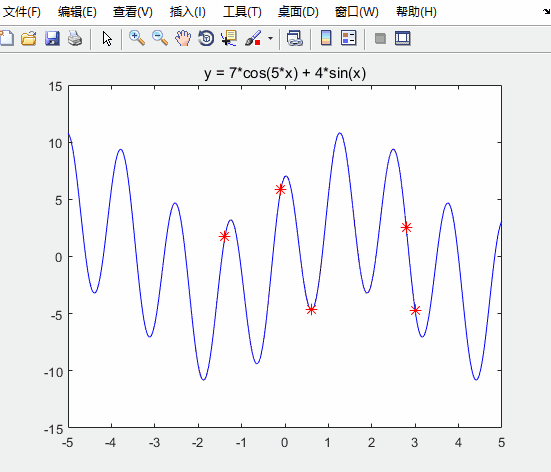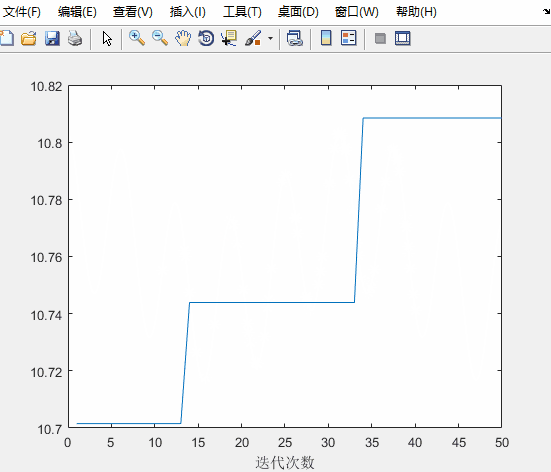
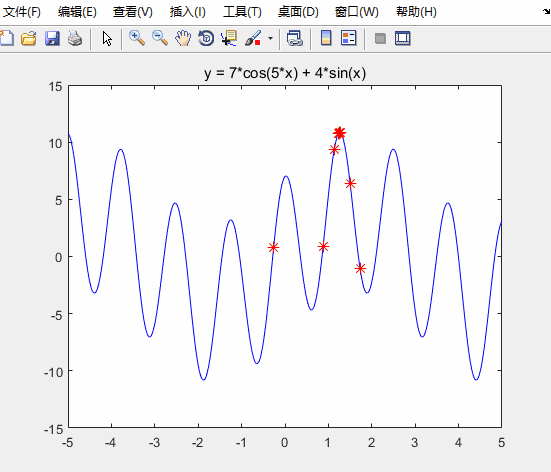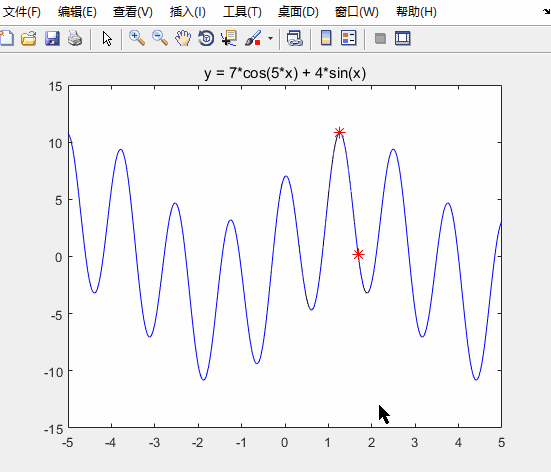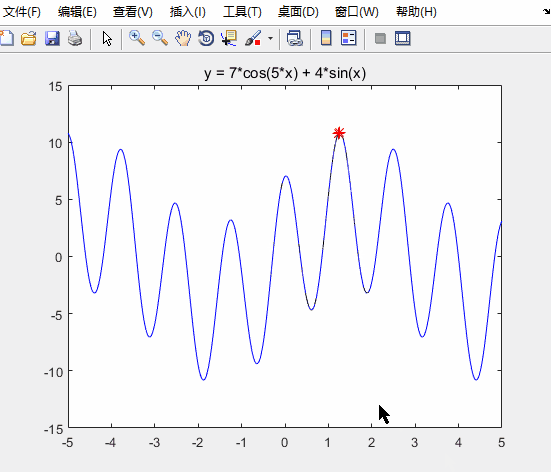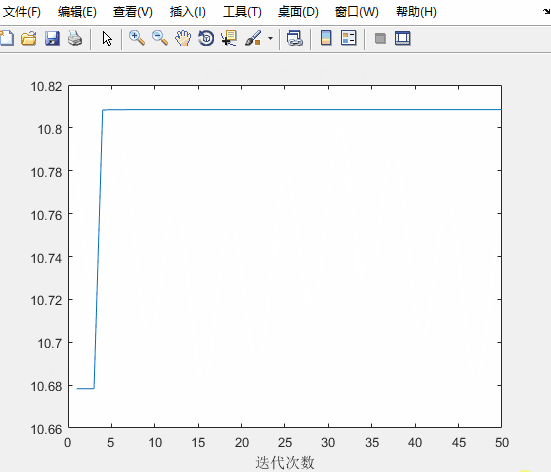
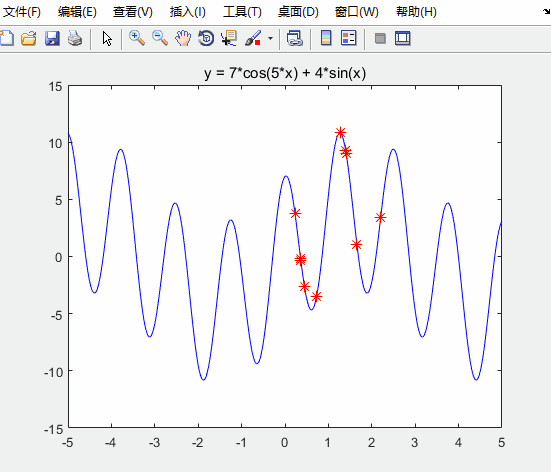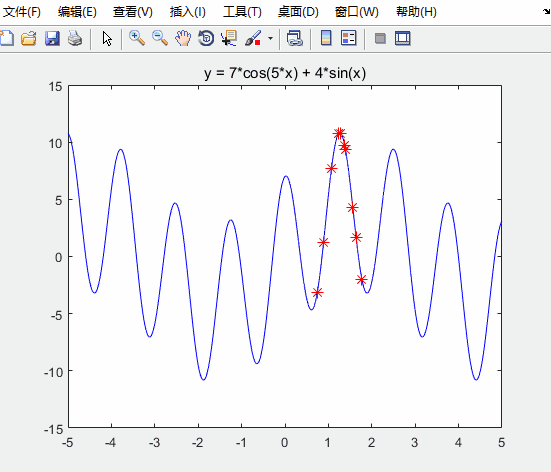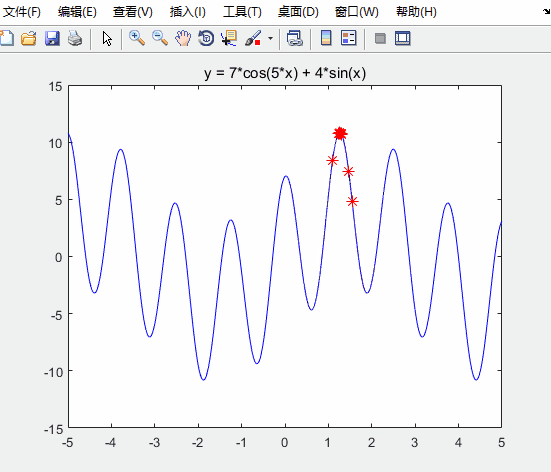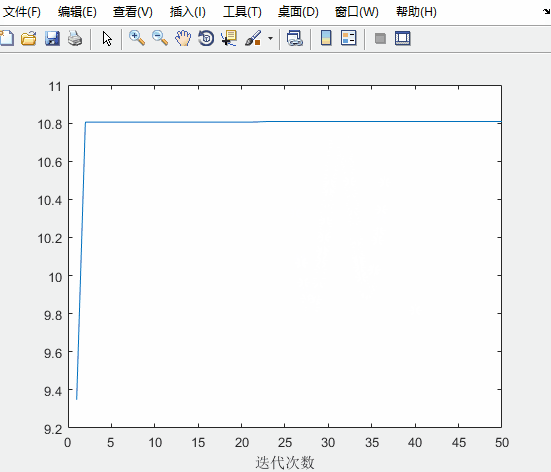
figure(2)
plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun1(gbest))
function y = Obj_fun1(x)
y = 7*cos(5*x) + 4*sin(x);
end
运行结果如下
对比未经优化的粒子群算法
可知：求得的最优解更接近实际最优解
参考论文：Shi, Y. and Eberhart, R.C. (1999) Empirical Study of Particle Swarm Optimization. Proceedings of the 1999 Congress on Evolutionary Computation, Washington DC, 6‐9 July 1999, 1945‐1950.