牢记公式，ardupilot EKF2就是纸老虎（四）！
版权声明：本文为博主原创文章，转载请附上博文链接！
四、一睹EKF2芳容
因为篇幅过长，写的一些公式会乱码，没办法只能把《 牢记公式，ardupilot EKF2就是纸老虎！》分成几个部分来写，深入了解EKF2,公式很重要，所以我将《 牢记公式，ardupilot EKF2就是纸老虎（三）！》中的公式再重复一遍。
在EKF2实际的应用中，过程噪声矩阵
中有些元素是非加性的，有些不是。观测噪声矩阵
中的元素都是加性的，所以上面的公式可以化简为如下公式：
预测
预测状态估计：
预测协方差估计：
更新
创新或计算剩余
创新（或残差）协方差
接近最优的卡尔曼增益
更新状态估计
更新的协方差估计
状态转移矩阵和观测矩阵被定义为以下雅克比行列式：
矩阵
被定义为以下雅克比行列式：
状态转移模型和观测模型如下：
过程噪声矩阵
有些元素加的是
有些加的是
。
看完《 牢记公式，ardupilot EKF2就是纸老虎（三）！》后，你知道了EKF2的代码虽然很多，又分布在不同的文件中，但它们都是围绕这上述的这几个公式进行的。也许到目前为止，你觉得EKF2也不过如此，不是很难嘛，也就这几个公式。如果这样想，你就大错特错了。前面讲到的只是EKF2使用的公式。下面我们结合GenerateNavFilterEquations.m和EKF2相关的代码来逐个的看看公式中的函数、矩阵分别都是什么。
预测过程
首先我们来确定EKF算法预测过程两个方程（预测状态估计方程和预测协方差估计方程）中的函数和变量。也就是状态向量
、函数
、状态转移矩阵
、协方差矩阵
、过程噪声协方差矩阵
和不知名的矩阵
。其中和的初值是根据相关传感器和被估计量的特性定出来的，具体为什么定的是代码中写的那些值，我目前也不清楚。
定义状态向量：
总共有24个状态，分别是以旋转矢量表示的三轴角度误差、三轴速度（北东地坐标系）、三轴位置（北东地坐标系，以滤波器开始运行的点为坐标原点）、陀螺仪三轴偏差、陀螺仪三轴比例因子、加速度计Z轴偏差、三轴地磁场（地磁场在北东地坐标系下的三轴分量）、三轴磁偏量（磁罗盘和机体坐标系没有对齐而产生的偏差，注意body_magfield表示的并不是磁罗盘测试出的三轴磁分量！！！）、两轴风速（北东地坐标系下的北和东）。四元数并不在状态向量中。
//本代码段在AP_NavEKF2_core.h中
// the states are available in two forms, either as a Vector31, or
// broken down as individual elements. Both are equivalent (same
// memory)
Vector28 statesArray;
struct state_elements {
Vector3f angErr; // 0..2
Vector3f velocity; // 3..5
Vector3f position; // 6..8
Vector3f gyro_bias; // 9..11
Vector3f gyro_scale; // 12..14
float accel_zbias; // 15
Vector3f earth_magfield; // 16..18
Vector3f body_magfield; // 19..21
Vector2f wind_vel; // 22..23
Quaternion quat; // 24..27
} &stateStruct; 定义协方差矩阵：
// initialise the covariance matrix
void NavEKF2_core::CovarianceInit()
{
// zero the matrix
memset(P, 0, sizeof(P));
// attitude error
P[0][0] = 0.1f;
P[1][1] = 0.1f;
P[2][2] = 0.1f;
// velocities
P[3][3] = sq(frontend->_gpsHorizVelNoise);
P[4][4] = P[3][3];
P[5][5] = sq(frontend->_gpsVertVelNoise);
// positions
P[6][6] = sq(frontend->_gpsHorizPosNoise);
P[7][7] = P[6][6];
P[8][8] = sq(frontend->_baroAltNoise);
// gyro delta angle biases
P[9][9] = sq(radians(InitialGyroBiasUncertainty() * dtEkfAvg));
P[10][10] = P[9][9];
P[11][11] = P[9][9];
// gyro scale factor biases
P[12][12] = sq(1e-3);
P[13][13] = P[12][12];
P[14][14] = P[12][12];
// Z delta velocity bias
P[15][15] = sq(INIT_ACCEL_BIAS_UNCERTAINTY * dtEkfAvg);
// earth magnetic field
P[16][16] = 0.0f;
P[17][17] = P[16][16];
P[18][18] = P[16][16];
// body magnetic field
P[19][19] = 0.0f;
P[20][20] = P[19][19];
P[21][21] = P[19][19];
// wind velocities
P[22][22] = 0.0f;
P[23][23] = P[22][22];
// optical flow ground height covariance
Popt = 0.25f;
} 定义过程噪声协方差矩阵，其中三轴角度误差、三轴速度（北东地坐标系）、三轴位置（北东地坐标系）的噪声是非加性的，在SG中，所以24维向量processNoise的前9个元素是0。
//本段代码在函数NavEKF2_core::CovariancePrediction()中
// use filtered height rate to increase wind process noise when climbing or descending
// this allows for wind gradient effects.
windVelSigma = dt * constrain_float(frontend->_windVelProcessNoise, 0.0f, 1.0f) * (1.0f + constrain_float(frontend->_wndVarHgtRateScale, 0.0f, 1.0f) * fabsf(hgtRate));
dAngBiasSigma = sq(dt) * constrain_float(frontend->_gyroBiasProcessNoise, 0.0f, 1.0f);
dVelBiasSigma = sq(dt) * constrain_float(frontend->_accelBiasProcessNoise, 0.0f, 1.0f);
dAngScaleSigma = dt * constrain_float(frontend->_gyroScaleProcessNoise, 0.0f, 1.0f);
magEarthSigma = dt * constrain_float(frontend->_magEarthProcessNoise, 0.0f, 1.0f);
magBodySigma = dt * constrain_float(frontend->_magBodyProcessNoise, 0.0f, 1.0f);
for (uint8_t i= 0; i<=8; i++) processNoise[i] = 0.0f;
for (uint8_t i=9; i<=11; i++) processNoise[i] = dAngBiasSigma;
for (uint8_t i=12; i<=14; i++) processNoise[i] = dAngScaleSigma;
if (expectGndEffectTakeoff) {
processNoise[15] = 0.0f;
} else {
processNoise[15] = dVelBiasSigma;
}
for (uint8_t i=16; i<=18; i++) processNoise[i] = magEarthSigma;
for (uint8_t i=19; i<=21; i++) processNoise[i] = magBodySigma;
for (uint8_t i=22; i<=23; i++) processNoise[i] = windVelSigma;
for (uint8_t i= 0; i<=stateIndexLim; i++) processNoise[i] = sq(processNoise[i]);
下面的一段代码出自GenerateNavFilterEquations.m，它的作用是定义了，进而推导出了状态转移矩阵、和。EKF2所用到的核心公式，全部出自这个matlab脚本，各个矩阵的组成也是matlab算出来的。
% IMPORTANT - This script requires the Matlab symbolic toolbox and takes ~3 hours to run
% Derivation of Navigation EKF using a local NED earth Tangent Frame and
% XYZ body fixed frame
% Sequential fusion of velocity and position measurements
% Fusion of true airspeed
% Sequential fusion of magnetic flux measurements
% 24 state architecture.
% IMU data is assumed to arrive at a constant rate with a time step of dt
% IMU delta angle and velocity data are used as control inputs,
% not observations
% Author: Paul Riseborough
% Based on use of a rotation vector for attitude estimation as described
% here:
% Mark E. Pittelkau. "Rotation Vector in Attitude Estimation",
% Journal of Guidance, Control, and Dynamics, Vol. 26, No. 6 (2003),
% pp. 855-860.
% State vector:
% error rotation vector in body frame (X,Y,Z)
% Velocity - m/sec (North, East, Down)
% Position - m (North, East, Down)
% Delta Angle bias - rad (X,Y,Z)
% Delta Angle scale factor (X,Y,Z)
% Delta Velocity bias - m/s (Z)
% Earth Magnetic Field Vector - (North, East, Down)
% Body Magnetic Field Vector - (X,Y,Z)
% Wind Vector - m/sec (North,East)
% Observations:
% NED velocity - m/s
% NED position - m
% True airspeed - m/s
% angle of sideslip - rad
% XYZ magnetic flux
% Time varying parameters:
% XYZ delta angle measurements in body axes - rad
% XYZ delta velocity measurements in body axes - m/sec
%% define symbolic variables and constants
clear all;
reset(symengine);
syms dax day daz 'real' % IMU delta angle measurements in body axes - rad
syms dvx dvy dvz 'real' % IMU delta velocity measurements in body axes - m/sec
syms q0 q1 q2 q3 'real' % quaternions defining attitude of body axes relative to local NED
syms vn ve vd 'real' % NED velocity - m/sec
syms pn pe pd 'real' % NED position - m
syms dax_b day_b daz_b 'real' % delta angle bias - rad
syms dax_s day_s daz_s 'real' % delta angle scale factor
syms dvz_b dvy_b dvz_b 'real' % delta velocity bias - m/sec
syms dt 'real' % IMU time step - sec
syms gravity 'real' % gravity - m/sec^2
syms daxNoise dayNoise dazNoise dvxNoise dvyNoise dvzNoise 'real'; % IMU delta angle and delta velocity measurement noise
syms vwn vwe 'real'; % NE wind velocity - m/sec
syms magX magY magZ 'real'; % XYZ body fixed magnetic field measurements - milligauss
syms magN magE magD 'real'; % NED earth fixed magnetic field components - milligauss
syms R_VN R_VE R_VD 'real' % variances for NED velocity measurements - (m/sec)^2
syms R_PN R_PE R_PD 'real' % variances for NED position measurements - m^2
syms R_TAS 'real' % variance for true airspeed measurement - (m/sec)^2
syms R_MAG 'real' % variance for magnetic flux measurements - milligauss^2
syms R_BETA 'real' % variance of sidelsip measurements rad^2
syms R_LOS 'real' % variance of LOS angular rate mesurements (rad/sec)^2
syms ptd 'real' % location of terrain in D axis
syms rotErrX rotErrY rotErrZ 'real'; % error rotation vector in body frame
syms decl 'real'; % earth magnetic field declination from true north 磁偏角
syms R_DECL R_YAW 'real'; % variance of declination or yaw angle observation
syms BCXinv BCYinv 'real' % inverse of ballistic coefficient for wind relative movement along the x and y body axes
syms rho 'real' % air density (kg/m^3)
syms R_ACC 'real' % variance of accelerometer measurements (m/s^2)^2
syms Kaccx Kaccy 'real' % derivative of X and Y body specific forces wrt componenent of true airspeed along each axis (1/s)
%% define the state prediction equations
% define the measured Delta angle and delta velocity vectors
dAngMeas = [dax; day; daz];
dVelMeas = [dvx; dvy; dvz];
% define the IMU bias errors and scale factor
dAngBias = [dax_b; day_b; daz_b];
dAngScale = [dax_s; day_s; daz_s];
dVelBias = [0;0;dvz_b];
% define the quaternion rotation vector for the state estimate
estQuat = [q0;q1;q2;q3];
% define the attitude error rotation vector, where error = truth - estimate
errRotVec = [rotErrX;rotErrY;rotErrZ];
% define the attitude error quaternion using a first order linearisation
errQuat = [1;0.5*errRotVec];
% Define the truth quaternion as the estimate + error
truthQuat = QuatMult(estQuat, errQuat);
% derive the truth body to nav direction cosine matrix
Tbn = Quat2Tbn(truthQuat);
% define the truth delta angle
% ignore coning compensation as these effects are negligible in terms of
% covariance growth for our application and grade of sensor
dAngTruth = dAngMeas.*dAngScale - dAngBias - [daxNoise;dayNoise;dazNoise];
% define the attitude update equations
% use a first order expansion of rotation to calculate the quaternion increment
% acceptable for propagation of covariances
deltaQuat = [1;
0.5*dAngTruth(1);
0.5*dAngTruth(2);
0.5*dAngTruth(3);
];
truthQuatNew = QuatMult(truthQuat,deltaQuat);
% calculate the updated attitude error quaternion with respect to the previous estimate
errQuatNew = QuatDivide(truthQuatNew,estQuat);
% change to a rotaton vector - this is the error rotation vector updated state
errRotNew = 2 * [errQuatNew(2);errQuatNew(3);errQuatNew(4)];
% Define the truth delta velocity -ignore sculling and transport rate
% corrections as these negligible are in terms of covariance growth for our
% application and grade of sensor
dVelTruth = dVelMeas - dVelBias - [dvxNoise;dvyNoise;dvzNoise];
% define the velocity update equations
% ignore coriolis terms for linearisation purposes
vNew = [vn;ve;vd] + [0;0;gravity]*dt + Tbn*dVelTruth;
% define the position update equations
pNew = [pn;pe;pd] + [vn;ve;vd]*dt;
% define the IMU error update equations
dabNew = [dax_b; day_b; daz_b];
dasNew = [dax_s; day_s; daz_s];
dvbNew = dvz_b;
% define the wind velocity update equations
vwnNew = vwn;
vweNew = vwe;
% define the earth magnetic field update equations
magNnew = magN;
magEnew = magE;
magDnew = magD;
% define the body magnetic field update equations
magXnew = magX;
magYnew = magY;
magZnew = magZ;
% Define the state vector & number of states
stateVector = [errRotVec;vn;ve;vd;pn;pe;pd;dax_b;day_b;daz_b;dax_s;day_s;daz_s;dvz_b;magN;magE;magD;magX;magY;magZ;vwn;vwe];
nStates=numel(stateVector);
% Define vector of process equations
newStateVector = [errRotNew;vNew;pNew;dabNew;dasNew;dvbNew;magNnew;magEnew;magDnew;magXnew;magYnew;magZnew;vwnNew;vweNew];
% derive the state transition matrix
F = jacobian(newStateVector, stateVector);
% set the rotation error states to zero
F = subs(F, {'rotErrX', 'rotErrY', 'rotErrZ'}, {0,0,0});
[F,SF]=OptimiseAlgebra(F,'SF');
% define a symbolic covariance matrix using strings to represent
% '_l_' to represent '( '
% '_c_' to represent ,
% '_r_' to represent ')'
% these can be substituted later to create executable code
for rowIndex = 1:nStates
for colIndex = 1:nStates
eval(['syms OP_l_',num2str(rowIndex),'_c_',num2str(colIndex), '_r_ real']);
eval(['P(',num2str(rowIndex),',',num2str(colIndex), ') = OP_l_',num2str(rowIndex),'_c_',num2str(colIndex),'_r_;']);
end
end
save 'StatePrediction.mat';
%% derive the covariance prediction equations
% This reduces the number of floating point operations by a factor of 6 or
% more compared to using the standard matrix operations in code
% Define the control (disturbance) vector. Error growth in the inertial
% solution is assumed to be driven by 'noise' in the delta angles and
% velocities, after bias effects have been removed. This is OK becasue we
% have sensor bias accounted for in the state equations.
distVector = [daxNoise;dayNoise;dazNoise;dvxNoise;dvyNoise;dvzNoise];
% derive the control(disturbance) influence matrix
G = jacobian(newStateVector, distVector);
G = subs(G, {'rotErrX', 'rotErrY', 'rotErrZ'}, {0,0,0});
[G,SG]=OptimiseAlgebra(G,'SG');
% derive the state error matrix
distMatrix = diag(distVector.^2);
Q = G*distMatrix*transpose(G);
[Q,SQ]=OptimiseAlgebra(Q,'SQ');
% remove the disturbance noise from the process equations as it is only
% needed when calculating the disturbance influence matrix
vNew = subs(vNew,{'daxNoise','dayNoise','dazNoise','dvxNoise','dvyNoise','dvzNoise'}, {0,0,0,0,0,0});
errRotNew = subs(errRotNew,{'daxNoise','dayNoise','dazNoise','dvxNoise','dvyNoise','dvzNoise'}, {0,0,0,0,0,0});
% Derive the predicted covariance matrix using the standard equation
PP = F*P*transpose(F) + Q;
% Collect common expressions to optimise processing
[PP,SPP]=OptimiseAlgebra(PP,'SPP');
save('StateAndCovariancePrediction.mat');
clear all;
reset(symengine);
首先这段脚本先定义了一大堆符号变量（通过syms dax day daz 'real' 这样的形式），注意这个符号变量和C/C++语言中的变量是有区别的，符号变量就是个符号（这么说好像有点绕），不用给它赋值，这个和高中数学里面解方程一样，比如
，
和
就是符号变量，当和等于不同值的时候
得到相应的值。这些符号变量组成了EKF公式中的函数和矩阵，在EKF2中这些符号变量，变成了变量，给相应的变量赋值后，经过运算得出了卡尔曼增益
和最后的状态估计向量
。matlab的结果是可以包含符号变量，这个功能实在是太好用了。也许是一直使用C++的原因，刚看这个脚本的时候，就符号变量这一点，想了好长时间才想明白。
接下来我先说下状态向量
，他的组成如下：
errRotVec = [rotErrX;rotErrY;rotErrZ];
stateVector = [errRotVec;vn;ve;vd;pn;pe;pd;dax_b;day_b;daz_b;dax_s;day_s;daz_s;dvz_b;magN;magE;magD;magX;magY;magZ;vwn;vwe] 状态向量中的每一个成员就相当于一个自变量，你可以把他们看成是
。
然后是新的状态向量
，其实就是由状态向量经过一些运算推导出来的。学术一点的说法就是通过一定的规则映射成。说到这里如果熟悉函数定义的你，应该已经明白了，就是。如果分开写的，（脚本定义中把角度误差、速度、位置分别写成了3维向量的格式）中的成员就是
。
newStateVector = [errRotNew;vNew;pNew;dabNew;dasNew;dvbNew;magNnew;magEnew;magDnew;magXnew;magYnew;magZnew;vwnNew;vweNew]; 有了
和
，接下来我们来看看每一个是怎么变成的（即
具体是什么）。
因为是对角度、速度、位置的修正，先定义了一些和这3个信息相关的变量
% define the measured Delta angle and delta velocity vectors
% dax, day, daz, dvx, dvy, dvz分别是陀螺仪和加速度计测出来的三轴角度增量和三轴速度增量（机体坐标系）
% 对应的dAngMeas和dVelMeas就是三轴角度增量和三轴速度增量组成的向量
dAngMeas = [dax; day; daz];
dVelMeas = [dvx; dvy; dvz];
% define the IMU bias errors and scale factor
% dax_b; day_b; daz_b; dax_s; day_s; daz_s; dvz_b分别是三轴角增量偏差、三轴陀螺仪比例因子和z轴速度偏差，几个数据是为了纠正对角度和速度的测量值
dAngBias = [dax_b; day_b; daz_b];
dAngScale = [dax_s; day_s; daz_s];
dVelBias = [0;0;dvz_b];
% define the quaternion rotation vector for the state estimate
% 定义表示姿态的四元数
estQuat = [q0;q1;q2;q3];
% define the attitude error rotation vector, where error = truth - estimate
% 定义表示姿态误差的旋转矢量
errRotVec = [rotErrX;rotErrY;rotErrZ];
% define the attitude error quaternion using a first order linearisation
% 定义和旋转矢量等效的四元数（欧拉角、四元数、方向余弦矩阵和旋转矢量是可以相互转换的）。
% 这种表示是一种近似的表示方法，具体的推导，我会在下面给出
errQuat = [1;0.5*errRotVec];
% Define the truth quaternion as the estimate + error
% 定义表示真是姿态角的四元数
truthQuat = QuatMult(estQuat, errQuat);
% derive the truth body to nav direction cosine matrix
% 定义坐标转换矩阵（即方向余弦矩阵），机体坐标系下的3维向量乘以这个矩阵的值就是这个向量在大地坐标系下的值，是不是很神奇。
Tbn = Quat2Tbn(truthQuat);
上面这一段的难点在于，陀螺仪测量的三轴角度增量和旋转矢量之间的转换，旋转矢量和四元数之间的关系。在论文RotationVectorinAttitudeEstimation中，似乎讲到了陀螺仪测量的三轴角度增量和旋转矢量的转换关系，不过我看了几遍也没看懂具体是怎么推导出来的。但结论应该是在角度增量很小时，陀螺仪测量的三轴角度增量和旋转矢量是相等的。
旋转矢量和四元数是有明确的转换关系的，公式如下
，其中
，
为旋转矢量，
为旋转矢量的长度。给上式化简一下为
，两边同除
，得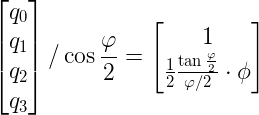
，假设旋转矢量是个特别小的值，趋于0时等于1,
等于1。最终假设是一个趋于0的小值时，旋转矢量和四元数的关系可以近似的写为
，即为脚本中定义的样子：
errQuat = [1;0.5*errRotVec];
旋转矢量和四元数的转换关系理顺了，下面就是一些高中的基本物理公式了。这里在多说一句，四元数的乘法和除法就是姿态的加或减，至于为什么是这样，我目前也没搞明白，先记住吧。
% define the truth delta angle
% ignore coning compensation as these effects are negligible in terms of
% covariance growth for our application and grade of sensor
% 真实角度增量 = 角度增量测量值 * 比例因子 - 三轴角度增量的偏差（补偿）- 测量噪声，这公式应该不难理解
dAngTruth = dAngMeas.*dAngScale - dAngBias - [daxNoise;dayNoise;dazNoise];
% define the attitude update equations
% use a first order expansion of rotation to calculate the quaternion increment
% acceptable for propagation of covariances
% 真实的角度增量转换为四元数，原理在上面已经讲解过了
deltaQuat = [1;
0.5*dAngTruth(1);
0.5*dAngTruth(2);
0.5*dAngTruth(3);
];
% 获得表示真实姿态角的四元数，四元数的乘法，就是姿态角的累加
truthQuatNew = QuatMult(truthQuat,deltaQuat);
% calculate the updated attitude error quaternion with respect to the previous estimate
% 角度误差四元数
errQuatNew = QuatDivide(truthQuatNew,estQuat);
% change to a rotaton vector - this is the error rotation vector updated state
% 根据之前所说的公式，反向推导的误差旋转矢量
errRotNew = 2 * [errQuatNew(2);errQuatNew(3);errQuatNew(4)];
% Define the truth delta velocity -ignore sculling and transport rate
% corrections as these negligible are in terms of covariance growth for our
% application and grade of sensor
% 真实三轴速度 = 三轴速度测量值 - 三轴速度偏差（补偿） - 速度测量噪声，角度和速度的测量都是在机体坐标系下进行的。
dVelTruth = dVelMeas - dVelBias - [dvxNoise;dvyNoise;dvzNoise];
% define the velocity update equations
% ignore coriolis terms for linearisation purposes
% 本时刻速度（北东地坐标系） = 上一时刻速度 + 重力加速度产生的速度 + 由机体坐标系转换到导航坐标系（北东地坐标系）下的速度
vNew = [vn;ve;vd] + [0;0;gravity]*dt + Tbn*dVelTruth;
% define the position update equations
% 本时刻的位置 = 上一时刻的位置 + 本时刻的速度*时间间隔
pNew = [pn;pe;pd] + [vn;ve;vd]*dt;
% 下面的这些量，假设它们不变
% define the IMU error update equations
dabNew = [dax_b; day_b; daz_b];
dasNew = [dax_s; day_s; daz_s];
dvbNew = dvz_b;
% define the wind velocity update equations
vwnNew = vwn;
vweNew = vwe;
% define the earth magnetic field update equations
magNnew = magN;
magEnew = magE;
magDnew = magD;
% define the body magnetic field update equations
magXnew = magX;
magYnew = magY;
magZnew = magZ;
确定了和后，实际上就确定了 ，根据
和
就能够算出状态转移矩阵、协方差矩阵、过程噪声协方差矩阵和不知名的矩阵。
% Define the state vector & number of states
% 定义状态向量
stateVector = [errRotVec;vn;ve;vd;pn;pe;pd;dax_b;day_b;daz_b;dax_s;day_s;daz_s;dvz_b;magN;magE;magD;magX;magY;magZ;vwn;vwe];
nStates=numel(stateVector);
% Define vector of process equations
% 定义新的状态向量
newStateVector = [errRotNew;vNew;pNew;dabNew;dasNew;dvbNew;magNnew;magEnew;magDnew;magXnew;magYnew;magZnew;vwnNew;vweNew];
% derive the state transition matrix
% 求解雅克比矩阵（即状态转移矩阵）
F = jacobian(newStateVector, stateVector);
% set the rotation error states to zero
% 设置旋转矢量为0
F = subs(F, {'rotErrX', 'rotErrY', 'rotErrZ'}, {0,0,0});
% 简化状态转移矩阵F，将F中的元素提取成一个个因子赋值给SF，然后用SF表示F
[F,SF]=OptimiseAlgebra(F,'SF');
% define a symbolic covariance matrix using strings to represent
% '_l_' to represent '( '
% '_c_' to represent ,
% '_r_' to represent ')'
% these can be substituted later to create executable code
% 定义初始的协方差矩阵P，其元素全部是符号变量，matlab中的矩阵、向量下标都是从1开始
for rowIndex = 1:nStates
for colIndex = 1:nStates
eval(['syms OP_l_',num2str(rowIndex),'_c_',num2str(colIndex), '_r_ real']);
eval(['P(',num2str(rowIndex),',',num2str(colIndex), ') = OP_l_',num2str(rowIndex),'_c_',num2str(colIndex),'_r_;']);
end
end
save 'StatePrediction.mat';
%% derive the covariance prediction equations
% This reduces the number of floating point operations by a factor of 6 or
% more compared to using the standard matrix operations in code
% Define the control (disturbance) vector. Error growth in the inertial
% solution is assumed to be driven by 'noise' in the delta angles and
% velocities, after bias effects have been removed. This is OK becasue we
% have sensor bias accounted for in the state equations.
% 定义测量（角度、速度）噪声矢量
distVector = [daxNoise;dayNoise;dazNoise;dvxNoise;dvyNoise;dvzNoise];
% derive the control(disturbance) influence matrix
% 求解博客中提到的矩阵L，他这里用G表示
G = jacobian(newStateVector, distVector);
% 化简矩阵G，提取公因子SG，并用SG表示G
G = subs(G, {'rotErrX', 'rotErrY', 'rotErrZ'}, {0,0,0});
[G,SG]=OptimiseAlgebra(G,'SG');
% derive the state error matrix
% 通过测量（角度、速度）噪声，生成过程噪声协方差矩阵
distMatrix = diag(distVector.^2);
% 通过公式计算新的过程噪声协方差矩阵Q
Q = G*distMatrix*transpose(G);
% 提取公因子，赋值SQ，并用SQ表示Q
[Q,SQ]=OptimiseAlgebra(Q,'SQ');
% remove the disturbance noise from the process equations as it is only
% needed when calculating the disturbance influence matrix
% 清零向量vNew中指定元素的值
vNew = subs(vNew,{'daxNoise','dayNoise','dazNoise','dvxNoise','dvyNoise','dvzNoise'}, {0,0,0,0,0,0});
% 清零向量errRotNew中指定元素的值
errRotNew = subs(errRotNew,{'daxNoise','dayNoise','dazNoise','dvxNoise','dvyNoise','dvzNoise'}, {0,0,0,0,0,0});
% Derive the predicted covariance matrix using the standard equation
% 根据公式，更新预测协方差估计
PP = F*P*transpose(F) + Q;
% Collect common expressions to optimise processing
% 简化矩阵PP,提取公因子，赋值SPP，并用SPP简化PP
[PP,SPP]=OptimiseAlgebra(PP,'SPP');
%将上述变量保存到StateAndCovariancePrediction.mat文件中，matlab这工具确实挺牛逼，你在matlab中加载这个文件，输入上述任意一个变量，他会返回这个变量的值
save('StateAndCovariancePrediction.mat');
matlab生成的状态转移矩阵
F =
[ 2*q0*SF(9) + 2*q2*SF(12) + 2*q1*SF(14) + 2*q3*SF(15), 2*q3*SF(8) - 2*q0*SF(7) + 2*q1*SF(11) - 2*q2*SF(13), 2*q1*SF(4) - 2*q2*SF(5) - 2*q3*SF(6) + 2*q0*SF(10), 0, 0, 0, 0, 0, 0, SF(16), 0, 0, dax*q0^2 + dax*q1^2 + dax*q3^2 + dax*SF(20), 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 2*q0*SF(15) - 2*q1*SF(12) - 2*q3*SF(9) + 2*q2*SF(14), 2*q0*SF(8) + 2*q3*SF(7) + 2*q2*SF(11) + 2*q1*SF(13), 2*q1*SF(5) - 2*q0*SF(6) + 2*q2*SF(4) - 2*q3*SF(10), 0, 0, 0, 0, 0, 0, 0, SF(16), 0, 0, day*q0^2 + day*q1^2 + day*q3^2 + day*SF(20), 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 2*q2*SF(9) - 2*q0*SF(12) - 2*q1*SF(15) + 2*q3*SF(14), 2*q0*SF(13) - 2*q2*SF(7) - 2*q1*SF(8) + 2*q3*SF(11), 2*q0*SF(5) + 2*q1*SF(6) + 2*q3*SF(4) + 2*q2*SF(10), 0, 0, 0, 0, 0, 0, 0, 0, SF(16), 0, 0, daz*q0^2 + daz*q1^2 + daz*q3^2 + daz*SF(20), 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ SF(19)*(2*q0*q2 + 2*q1*q3) + SF(17)*(SF(25) - 2*q0*q3), SF(17)*SF(24) - SF(18)*(2*q0*q2 + 2*q1*q3), SF(19)*SF(24) + SF(18)*(SF(25) - 2*q0*q3), 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, - 2*q0*q2 - 2*q1*q3, 0, 0, 0, 0, 0, 0, 0, 0]
[ SF(17)*SF(22) - SF(19)*SF(23), SF(18)*SF(23) - SF(17)*(SF(25) + 2*q0*q3), SF(18)*SF(22) - SF(19)*(SF(25) + 2*q0*q3), 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, SF(23), 0, 0, 0, 0, 0, 0, 0, 0]
[ SF(17)*(2*q0*q1 + 2*q2*q3) - SF(19)*SF(21), SF(18)*SF(21) + SF(17)*(2*q0*q2 - 2*q1*q3), SF(18)*(2*q0*q1 + 2*q2*q3) + SF(19)*(2*q0*q2 - 2*q1*q3), 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, SF(21), 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, dt, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, dt, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, dt, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]SF =
daz_b/2 + dazNoise/2 - (daz*daz_s)/2
day_b/2 + dayNoise/2 - (day*day_s)/2
dax_b/2 + daxNoise/2 - (dax*dax_s)/2
q3/2 - (q0*SF(1))/2 + (q1*SF(2))/2 - (q2*SF(3))/2
q0/2 - (q1*SF(3))/2 - (q2*SF(2))/2 + (q3*SF(1))/2
q1/2 + (q0*SF(3))/2 - (q2*SF(1))/2 - (q3*SF(2))/2
q3/2 + (q0*SF(1))/2 - (q1*SF(2))/2 - (q2*SF(3))/2
q0/2 - (q1*SF(3))/2 + (q2*SF(2))/2 - (q3*SF(1))/2
q0/2 + (q1*SF(3))/2 - (q2*SF(2))/2 - (q3*SF(1))/2
q2/2 + (q0*SF(2))/2 + (q1*SF(1))/2 + (q3*SF(3))/2
q2/2 - (q0*SF(2))/2 - (q1*SF(1))/2 + (q3*SF(3))/2
q2/2 + (q0*SF(2))/2 - (q1*SF(1))/2 - (q3*SF(3))/2
q1/2 + (q0*SF(3))/2 + (q2*SF(1))/2 + (q3*SF(2))/2
q1/2 - (q0*SF(3))/2 + (q2*SF(1))/2 - (q3*SF(2))/2
q3/2 + (q0*SF(1))/2 + (q1*SF(2))/2 + (q2*SF(3))/2
- q0^2 - q1^2 - q2^2 - q3^2
dvz_b - dvz + dvzNoise
dvx - dvxNoise
dvy - dvyNoise
q2^2
- q0^2 + q1^2 - q3^2 + SF(20)
q0^2 - q1^2 - q3^2 + SF(20)
2*q0*q1 - 2*q2*q3
- q0^2 - q1^2 + q3^2 + SF(20)
2*q1*q2 EKF2代码中的
,两者相比，EKF2代码中的元素没有角度和速度测量噪声，至于为啥没有，我目前也不大清楚。
// calculate the predicted covariance due to inertial sensor error propagation
// we calculate the upper diagonal and copy to take advantage of symmetry
SF[0] = daz_b/2 - (daz*daz_s)/2;
SF[1] = day_b/2 - (day*day_s)/2;
SF[2] = dax_b/2 - (dax*dax_s)/2;
SF[3] = q3/2 - (q0*SF[0])/2 + (q1*SF[1])/2 - (q2*SF[2])/2;
SF[4] = q0/2 - (q1*SF[2])/2 - (q2*SF[1])/2 + (q3*SF[0])/2;
SF[5] = q1/2 + (q0*SF[2])/2 - (q2*SF[0])/2 - (q3*SF[1])/2;
SF[6] = q3/2 + (q0*SF[0])/2 - (q1*SF[1])/2 - (q2*SF[2])/2;
SF[7] = q0/2 - (q1*SF[2])/2 + (q2*SF[1])/2 - (q3*SF[0])/2;
SF[8] = q0/2 + (q1*SF[2])/2 - (q2*SF[1])/2 - (q3*SF[0])/2;
SF[9] = q2/2 + (q0*SF[1])/2 + (q1*SF[0])/2 + (q3*SF[2])/2;
SF[10] = q2/2 - (q0*SF[1])/2 - (q1*SF[0])/2 + (q3*SF[2])/2;
SF[11] = q2/2 + (q0*SF[1])/2 - (q1*SF[0])/2 - (q3*SF[2])/2;
SF[12] = q1/2 + (q0*SF[2])/2 + (q2*SF[0])/2 + (q3*SF[1])/2;
SF[13] = q1/2 - (q0*SF[2])/2 + (q2*SF[0])/2 - (q3*SF[1])/2;
SF[14] = q3/2 + (q0*SF[0])/2 + (q1*SF[1])/2 + (q2*SF[2])/2;
SF[15] = - sq(q0) - sq(q1) - sq(q2) - sq(q3);
SF[16] = dvz_b - dvz;
SF[17] = dvx;
SF[18] = dvy;
SF[19] = sq(q2);
SF[20] = SF[19] - sq(q0) + sq(q1) - sq(q3);
SF[21] = SF[19] + sq(q0) - sq(q1) - sq(q3);
SF[22] = 2*q0*q1 - 2*q2*q3;
SF[23] = SF[19] - sq(q0) - sq(q1) + sq(q3);
SF[24] = 2*q1*q2; matlab生成的矩阵
，在matlab脚本中是
G =
[ SG(1), 0, 0, 0, 0, 0]
[ 0, SG(1), 0, 0, 0, 0]
[ 0, 0, SG(1), 0, 0, 0]
[ 0, 0, 0, SG(2) + SG(3) - SG(4) - SG(5), 2*q0*q3 - 2*q1*q2, - 2*q0*q2 - 2*q1*q3]
[ 0, 0, 0, - 2*q0*q3 - 2*q1*q2, SG(2) - SG(3) + SG(4) - SG(5), 2*q0*q1 - 2*q2*q3]
[ 0, 0, 0, 2*q0*q2 - 2*q1*q3, - 2*q0*q1 - 2*q2*q3, SG(3) - SG(2) + SG(4) - SG(5)]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0]
SG =
- q0^2 - q1^2 - q2^2 - q3^2
q3^2
q2^2
q1^2
q0^2 EKF2代码中的
SG[0] = - sq(q0) - sq(q1) - sq(q2) - sq(q3);
SG[1] = sq(q3);
SG[2] = sq(q2);
SG[3] = sq(q1);
SG[4] = sq(q0); matlab生成的过程噪声协方差矩阵
Q =
[ daxNoise^2*SQ(4), 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, dayNoise^2*SQ(4), 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, dazNoise^2*SQ(4), 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, SQ(6)*(SQ(9) + 2*q0*q2)^2 + SQ(5)*(SQ(10) - 2*q0*q3)^2 + SQ(7)*(SG(2) + SG(3) - SG(4) - SG(5))^2, SQ(3), SQ(2), 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, SQ(3), SQ(6)*(SQ(8) - 2*q0*q1)^2 + SQ(7)*(SQ(10) + 2*q0*q3)^2 + SQ(5)*(SG(2) - SG(3) + SG(4) - SG(5))^2, SQ(1), 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, SQ(2), SQ(1), SQ(5)*(SQ(8) + 2*q0*q1)^2 + SQ(7)*(SQ(9) - 2*q0*q2)^2 + SQ(6)*(SG(2) - SG(3) - SG(4) + SG(5))^2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
SQ =
- (2*q0*q2 - 2*q1*q3)*(2*q0*q3 + 2*q1*q2)*dvxNoise^2 - (2*q0*q1 + 2*q2*q3)*(SG(2) - SG(3) + SG(4) - SG(5))*dvyNoise^2 - (2*q0*q1 - 2*q2*q3)*(SG(2) - SG(3) - SG(4) + SG(5))*dvzNoise^2
(2*q0*q2 - 2*q1*q3)*(SG(2) + SG(3) - SG(4) - SG(5))*dvxNoise^2 - (2*q0*q1 + 2*q2*q3)*(2*q0*q3 - 2*q1*q2)*dvyNoise^2 + (2*q0*q2 + 2*q1*q3)*(SG(2) - SG(3) - SG(4) + SG(5))*dvzNoise^2
- (2*q0*q3 + 2*q1*q2)*(SG(2) + SG(3) - SG(4) - SG(5))*dvxNoise^2 + (2*q0*q3 - 2*q1*q2)*(SG(2) - SG(3) + SG(4) - SG(5))*dvyNoise^2 - (2*q0*q1 - 2*q2*q3)*(2*q0*q2 + 2*q1*q3)*dvzNoise^2
SG(1)^2
dvyNoise^2
dvzNoise^2
dvxNoise^2
2*q2*q3
2*q1*q3
2*q1*q2 EKF2代码中的
，EKF2代码中和matlab脚本中的不一致，目前还不清楚是什么原因，有可能EKF2的这些公式是比较旧的GenerateNavFilterEquations.m生成的。也有可能虽然不一样，但最终生成的是一样的。这个脚本运行一次大约需要3个小时，等我有时间运行下，试试。
SQ[0] = - dvyNoise*(2*q0*q1 + 2*q2*q3)*(SG[1] - SG[2] + SG[3] - SG[4]) - dvzNoise*(2*q0*q1 - 2*q2*q3)*(SG[1] - SG[2] - SG[3] + SG[4]) - dvxNoise*(2*q0*q2 - 2*q1*q3)*(2*q0*q3 + 2*q1*q2);
SQ[1] = dvxNoise*(2*q0*q2 - 2*q1*q3)*(SG[1] + SG[2] - SG[3] - SG[4]) + dvzNoise*(2*q0*q2 + 2*q1*q3)*(SG[1] - SG[2] - SG[3] + SG[4]) - dvyNoise*(2*q0*q1 + 2*q2*q3)*(2*q0*q3 - 2*q1*q2);
SQ[2] = dvyNoise*(2*q0*q3 - 2*q1*q2)*(SG[1] - SG[2] + SG[3] - SG[4]) - dvxNoise*(2*q0*q3 + 2*q1*q2)*(SG[1] + SG[2] - SG[3] - SG[4]) - dvzNoise*(2*q0*q1 - 2*q2*q3)*(2*q0*q2 + 2*q1*q3);
SQ[3] = sq(SG[0]);
SQ[4] = 2*q2*q3;
SQ[5] = 2*q1*q3;
SQ[6] = 2*q1*q2;
SQ[7] = SG[4]; matlab生成的
实在是太大了，粘贴不过来，所以只能展示
了
SPP =
SF(18)*(2*q0*q1 + 2*q2*q3) + SF(19)*(2*q0*q2 - 2*q1*q3)
SF(19)*(2*q0*q2 + 2*q1*q3) + SF(17)*(SF(25) - 2*q0*q3)
2*q3*SF(9) + 2*q1*SF(12) - 2*q0*SF(15) - 2*q2*SF(14)
2*q1*SF(8) + 2*q2*SF(7) - 2*q0*SF(13) - 2*q3*SF(11)
2*q0*SF(7) - 2*q3*SF(8) - 2*q1*SF(11) + 2*q2*SF(13)
2*q0*SF(9) + 2*q2*SF(12) + 2*q1*SF(14) + 2*q3*SF(15)
2*q0*SF(8) + 2*q3*SF(7) + 2*q2*SF(11) + 2*q1*SF(13)
2*q1*SF(4) - 2*q2*SF(5) - 2*q3*SF(6) + 2*q0*SF(10)
2*q0*SF(6) - 2*q1*SF(5) - 2*q2*SF(4) + 2*q3*SF(10)
SF(19)*SF(21) - SF(17)*(2*q0*q1 + 2*q2*q3)
SF(18)*SF(21) + SF(17)*(2*q0*q2 - 2*q1*q3)
SF(18)*SF(22) - SF(19)*(SF(25) + 2*q0*q3)
SF(18)*SF(23) - SF(17)*(SF(25) + 2*q0*q3)
2*q0*SF(5) + 2*q1*SF(6) + 2*q3*SF(4) + 2*q2*SF(10)
2*q2*SF(9) - 2*q0*SF(12) - 2*q1*SF(15) + 2*q3*SF(14)
SF(19)*SF(24) + SF(18)*(SF(25) - 2*q0*q3)
daz*q0^2 + daz*q1^2 + daz*q3^2 + daz*SF(20)
day*q0^2 + day*q1^2 + day*q3^2 + day*SF(20)
dax*q0^2 + dax*q1^2 + dax*q3^2 + dax*SF(20)
SF(17)*SF(24) - SF(18)*(2*q0*q2 + 2*q1*q3)
SF(17)*SF(22) - SF(19)*SF(23)
2*q0*q2 + 2*q1*q3
SF(16) EKF2代码中的
SPP[0] = SF[17]*(2*q0*q1 + 2*q2*q3) + SF[18]*(2*q0*q2 - 2*q1*q3);
SPP[1] = SF[18]*(2*q0*q2 + 2*q1*q3) + SF[16]*(SF[24] - 2*q0*q3);
SPP[2] = 2*q3*SF[8] + 2*q1*SF[11] - 2*q0*SF[14] - 2*q2*SF[13];
SPP[3] = 2*q1*SF[7] + 2*q2*SF[6] - 2*q0*SF[12] - 2*q3*SF[10];
SPP[4] = 2*q0*SF[6] - 2*q3*SF[7] - 2*q1*SF[10] + 2*q2*SF[12];
SPP[5] = 2*q0*SF[8] + 2*q2*SF[11] + 2*q1*SF[13] + 2*q3*SF[14];
SPP[6] = 2*q0*SF[7] + 2*q3*SF[6] + 2*q2*SF[10] + 2*q1*SF[12];
SPP[7] = SF[18]*SF[20] - SF[16]*(2*q0*q1 + 2*q2*q3);
SPP[8] = 2*q1*SF[3] - 2*q2*SF[4] - 2*q3*SF[5] + 2*q0*SF[9];
SPP[9] = 2*q0*SF[5] - 2*q1*SF[4] - 2*q2*SF[3] + 2*q3*SF[9];
SPP[10] = SF[17]*SF[20] + SF[16]*(2*q0*q2 - 2*q1*q3);
SPP[11] = SF[17]*SF[21] - SF[18]*(SF[24] + 2*q0*q3);
SPP[12] = SF[17]*SF[22] - SF[16]*(SF[24] + 2*q0*q3);
SPP[13] = 2*q0*SF[4] + 2*q1*SF[5] + 2*q3*SF[3] + 2*q2*SF[9];
SPP[14] = 2*q2*SF[8] - 2*q0*SF[11] - 2*q1*SF[14] + 2*q3*SF[13];
SPP[15] = SF[18]*SF[23] + SF[17]*(SF[24] - 2*q0*q3);
SPP[16] = daz*SF[19] + daz*sq(q0) + daz*sq(q1) + daz*sq(q3);
SPP[17] = day*SF[19] + day*sq(q0) + day*sq(q1) + day*sq(q3);
SPP[18] = dax*SF[19] + dax*sq(q0) + dax*sq(q1) + dax*sq(q3);
SPP[19] = SF[16]*SF[23] - SF[17]*(2*q0*q2 + 2*q1*q3);
SPP[20] = SF[16]*SF[21] - SF[18]*SF[22];
SPP[21] = 2*q0*q2 + 2*q1*q3;
SPP[22] = SF[15];下面的代码执行的是
预测状态估计： 
/*
* Update the quaternion, velocity and position states using delayed IMU measurements
* because the EKF is running on a delayed time horizon. Note that the quaternion is
* not used by the EKF equations, which instead estimate the error in the attitude of
* the vehicle when each observtion is fused. This attitude error is then used to correct
* the quaternion.
*/
void NavEKF2_core::UpdateStrapdownEquationsNED()
{
// update the quaternion states by rotating from the previous attitude through
// the delta angle rotation quaternion and normalise
// apply correction for earth's rotation rate
// % * - and + operators have been overloaded
stateStruct.quat.rotate(delAngCorrected - prevTnb * earthRateNED*imuDataDelayed.delAngDT);
stateStruct.quat.normalize();
// transform body delta velocities to delta velocities in the nav frame
// use the nav frame from previous time step as the delta velocities
// have been rotated into that frame
// * and + operators have been overloaded
Vector3f delVelNav; // delta velocity vector in earth axes
delVelNav = prevTnb.mul_transpose(delVelCorrected);
delVelNav.z += GRAVITY_MSS*imuDataDelayed.delVelDT;
// calculate the body to nav cosine matrix
stateStruct.quat.inverse().rotation_matrix(prevTnb);
// calculate the rate of change of velocity (used for launch detect and other functions)
velDotNED = delVelNav / imuDataDelayed.delVelDT;
// apply a first order lowpass filter
velDotNEDfilt = velDotNED * 0.05f + velDotNEDfilt * 0.95f;
// calculate a magnitude of the filtered nav acceleration (required for GPS
// variance estimation)
accNavMag = velDotNEDfilt.length();
accNavMagHoriz = norm(velDotNEDfilt.x , velDotNEDfilt.y);
// if we are not aiding, then limit the horizontal magnitude of acceleration
// to prevent large manoeuvre transients disturbing the attitude
if ((PV_AidingMode == AID_NONE) && (accNavMagHoriz > 5.0f)) {
float gain = 5.0f/accNavMagHoriz;
delVelNav.x *= gain;
delVelNav.y *= gain;
}
// save velocity for use in trapezoidal integration for position calcuation
Vector3f lastVelocity = stateStruct.velocity;
// sum delta velocities to get velocity
stateStruct.velocity += delVelNav;
// apply a trapezoidal integration to velocities to calculate position
stateStruct.position += (stateStruct.velocity + lastVelocity) * (imuDataDelayed.delVelDT*0.5f);
// accumulate the bias delta angle and time since last reset by an OF measurement arrival
delAngBodyOF += delAngCorrected;
delTimeOF += imuDataDelayed.delAngDT;
// limit states to protect against divergence
ConstrainStates();
}
下面的代码执行的是
预测协方差估计： 
/*
* Calculate the predicted state covariance matrix using algebraic equations generated with Matlab symbolic toolbox.
* The script file used to generate these and other equations in this filter can be found here:
* https://github.com/priseborough/InertialNav/blob/master/derivations/RotationVectorAttitudeParameterisation/GenerateNavFilterEquations.m
*/
void NavEKF2_core::CovariancePrediction()
{
hal.util->perf_begin(_perf_CovariancePrediction);
float windVelSigma; // wind velocity 1-sigma process noise - m/s
float dAngBiasSigma;// delta angle bias 1-sigma process noise - rad/s
float dVelBiasSigma;// delta velocity bias 1-sigma process noise - m/s
float dAngScaleSigma;// delta angle scale factor 1-Sigma process noise
float magEarthSigma;// earth magnetic field 1-sigma process noise
float magBodySigma; // body magnetic field 1-sigma process noise
float daxNoise; // X axis delta angle noise variance rad^2
float dayNoise; // Y axis delta angle noise variance rad^2
float dazNoise; // Z axis delta angle noise variance rad^2
float dvxNoise; // X axis delta velocity variance noise (m/s)^2
float dvyNoise; // Y axis delta velocity variance noise (m/s)^2
float dvzNoise; // Z axis delta velocity variance noise (m/s)^2
float dvx; // X axis delta velocity (m/s)
float dvy; // Y axis delta velocity (m/s)
float dvz; // Z axis delta velocity (m/s)
float dax; // X axis delta angle (rad)
float day; // Y axis delta angle (rad)
float daz; // Z axis delta angle (rad)
float q0; // attitude quaternion
float q1; // attitude quaternion
float q2; // attitude quaternion
float q3; // attitude quaternion
float dax_b; // X axis delta angle measurement bias (rad)
float day_b; // Y axis delta angle measurement bias (rad)
float daz_b; // Z axis delta angle measurement bias (rad)
float dax_s; // X axis delta angle measurement scale factor
float day_s; // Y axis delta angle measurement scale factor
float daz_s; // Z axis delta angle measurement scale factor
float dvz_b; // Z axis delta velocity measurement bias (rad)
// calculate covariance prediction process noise
// use filtered height rate to increase wind process noise when climbing or descending
// this allows for wind gradient effects.
// filter height rate using a 10 second time constant filter
dt = imuDataDelayed.delAngDT;
float alpha = 0.1f * dt;
hgtRate = hgtRate * (1.0f - alpha) - stateStruct.velocity.z * alpha;
// use filtered height rate to increase wind process noise when climbing or descending
// this allows for wind gradient effects.
windVelSigma = dt * constrain_float(frontend->_windVelProcessNoise, 0.0f, 1.0f) * (1.0f + constrain_float(frontend->_wndVarHgtRateScale, 0.0f, 1.0f) * fabsf(hgtRate));
dAngBiasSigma = sq(dt) * constrain_float(frontend->_gyroBiasProcessNoise, 0.0f, 1.0f);
dVelBiasSigma = sq(dt) * constrain_float(frontend->_accelBiasProcessNoise, 0.0f, 1.0f);
dAngScaleSigma = dt * constrain_float(frontend->_gyroScaleProcessNoise, 0.0f, 1.0f);
magEarthSigma = dt * constrain_float(frontend->_magEarthProcessNoise, 0.0f, 1.0f);
magBodySigma = dt * constrain_float(frontend->_magBodyProcessNoise, 0.0f, 1.0f);
for (uint8_t i= 0; i<=8; i++) processNoise[i] = 0.0f;
for (uint8_t i=9; i<=11; i++) processNoise[i] = dAngBiasSigma;
for (uint8_t i=12; i<=14; i++) processNoise[i] = dAngScaleSigma;
if (expectGndEffectTakeoff) {
processNoise[15] = 0.0f;
} else {
processNoise[15] = dVelBiasSigma;
}
for (uint8_t i=16; i<=18; i++) processNoise[i] = magEarthSigma;
for (uint8_t i=19; i<=21; i++) processNoise[i] = magBodySigma;
for (uint8_t i=22; i<=23; i++) processNoise[i] = windVelSigma;
for (uint8_t i= 0; i<=stateIndexLim; i++) processNoise[i] = sq(processNoise[i]);
// set variables used to calculate covariance growth
dvx = imuDataDelayed.delVel.x;
dvy = imuDataDelayed.delVel.y;
dvz = imuDataDelayed.delVel.z;
dax = imuDataDelayed.delAng.x;
day = imuDataDelayed.delAng.y;
daz = imuDataDelayed.delAng.z;
q0 = stateStruct.quat[0];
q1 = stateStruct.quat[1];
q2 = stateStruct.quat[2];
q3 = stateStruct.quat[3];
dax_b = stateStruct.gyro_bias.x;
day_b = stateStruct.gyro_bias.y;
daz_b = stateStruct.gyro_bias.z;
dax_s = stateStruct.gyro_scale.x;
day_s = stateStruct.gyro_scale.y;
daz_s = stateStruct.gyro_scale.z;
dvz_b = stateStruct.accel_zbias;
float _gyrNoise = constrain_float(frontend->_gyrNoise, 0.0f, 1.0f);
daxNoise = dayNoise = dazNoise = sq(dt*_gyrNoise);
float _accNoise = constrain_float(frontend->_accNoise, 0.0f, 10.0f);
dvxNoise = dvyNoise = dvzNoise = sq(dt*_accNoise);
// calculate the predicted covariance due to inertial sensor error propagation
// we calculate the upper diagonal and copy to take advantage of symmetry
SF[0] = daz_b/2 - (daz*daz_s)/2;
SF[1] = day_b/2 - (day*day_s)/2;
SF[2] = dax_b/2 - (dax*dax_s)/2;
SF[3] = q3/2 - (q0*SF[0])/2 + (q1*SF[1])/2 - (q2*SF[2])/2;
SF[4] = q0/2 - (q1*SF[2])/2 - (q2*SF[1])/2 + (q3*SF[0])/2;
SF[5] = q1/2 + (q0*SF[2])/2 - (q2*SF[0])/2 - (q3*SF[1])/2;
SF[6] = q3/2 + (q0*SF[0])/2 - (q1*SF[1])/2 - (q2*SF[2])/2;
SF[7] = q0/2 - (q1*SF[2])/2 + (q2*SF[1])/2 - (q3*SF[0])/2;
SF[8] = q0/2 + (q1*SF[2])/2 - (q2*SF[1])/2 - (q3*SF[0])/2;
SF[9] = q2/2 + (q0*SF[1])/2 + (q1*SF[0])/2 + (q3*SF[2])/2;
SF[10] = q2/2 - (q0*SF[1])/2 - (q1*SF[0])/2 + (q3*SF[2])/2;
SF[11] = q2/2 + (q0*SF[1])/2 - (q1*SF[0])/2 - (q3*SF[2])/2;
SF[12] = q1/2 + (q0*SF[2])/2 + (q2*SF[0])/2 + (q3*SF[1])/2;
SF[13] = q1/2 - (q0*SF[2])/2 + (q2*SF[0])/2 - (q3*SF[1])/2;
SF[14] = q3/2 + (q0*SF[0])/2 + (q1*SF[1])/2 + (q2*SF[2])/2;
SF[15] = - sq(q0) - sq(q1) - sq(q2) - sq(q3);
SF[16] = dvz_b - dvz;
SF[17] = dvx;
SF[18] = dvy;
SF[19] = sq(q2);
SF[20] = SF[19] - sq(q0) + sq(q1) - sq(q3);
SF[21] = SF[19] + sq(q0) - sq(q1) - sq(q3);
SF[22] = 2*q0*q1 - 2*q2*q3;
SF[23] = SF[19] - sq(q0) - sq(q1) + sq(q3);
SF[24] = 2*q1*q2;
SG[0] = - sq(q0) - sq(q1) - sq(q2) - sq(q3);
SG[1] = sq(q3);
SG[2] = sq(q2);
SG[3] = sq(q1);
SG[4] = sq(q0);
SQ[0] = - dvyNoise*(2*q0*q1 + 2*q2*q3)*(SG[1] - SG[2] + SG[3] - SG[4]) - dvzNoise*(2*q0*q1 - 2*q2*q3)*(SG[1] - SG[2] - SG[3] + SG[4]) - dvxNoise*(2*q0*q2 - 2*q1*q3)*(2*q0*q3 + 2*q1*q2);
SQ[1] = dvxNoise*(2*q0*q2 - 2*q1*q3)*(SG[1] + SG[2] - SG[3] - SG[4]) + dvzNoise*(2*q0*q2 + 2*q1*q3)*(SG[1] - SG[2] - SG[3] + SG[4]) - dvyNoise*(2*q0*q1 + 2*q2*q3)*(2*q0*q3 - 2*q1*q2);
SQ[2] = dvyNoise*(2*q0*q3 - 2*q1*q2)*(SG[1] - SG[2] + SG[3] - SG[4]) - dvxNoise*(2*q0*q3 + 2*q1*q2)*(SG[1] + SG[2] - SG[3] - SG[4]) - dvzNoise*(2*q0*q1 - 2*q2*q3)*(2*q0*q2 + 2*q1*q3);
SQ[3] = sq(SG[0]);
SQ[4] = 2*q2*q3;
SQ[5] = 2*q1*q3;
SQ[6] = 2*q1*q2;
SQ[7] = SG[4];
SPP[0] = SF[17]*(2*q0*q1 + 2*q2*q3) + SF[18]*(2*q0*q2 - 2*q1*q3);
SPP[1] = SF[18]*(2*q0*q2 + 2*q1*q3) + SF[16]*(SF[24] - 2*q0*q3);
SPP[2] = 2*q3*SF[8] + 2*q1*SF[11] - 2*q0*SF[14] - 2*q2*SF[13];
SPP[3] = 2*q1*SF[7] + 2*q2*SF[6] - 2*q0*SF[12] - 2*q3*SF[10];
SPP[4] = 2*q0*SF[6] - 2*q3*SF[7] - 2*q1*SF[10] + 2*q2*SF[12];
SPP[5] = 2*q0*SF[8] + 2*q2*SF[11] + 2*q1*SF[13] + 2*q3*SF[14];
SPP[6] = 2*q0*SF[7] + 2*q3*SF[6] + 2*q2*SF[10] + 2*q1*SF[12];
SPP[7] = SF[18]*SF[20] - SF[16]*(2*q0*q1 + 2*q2*q3);
SPP[8] = 2*q1*SF[3] - 2*q2*SF[4] - 2*q3*SF[5] + 2*q0*SF[9];
SPP[9] = 2*q0*SF[5] - 2*q1*SF[4] - 2*q2*SF[3] + 2*q3*SF[9];
SPP[10] = SF[17]*SF[20] + SF[16]*(2*q0*q2 - 2*q1*q3);
SPP[11] = SF[17]*SF[21] - SF[18]*(SF[24] + 2*q0*q3);
SPP[12] = SF[17]*SF[22] - SF[16]*(SF[24] + 2*q0*q3);
SPP[13] = 2*q0*SF[4] + 2*q1*SF[5] + 2*q3*SF[3] + 2*q2*SF[9];
SPP[14] = 2*q2*SF[8] - 2*q0*SF[11] - 2*q1*SF[14] + 2*q3*SF[13];
SPP[15] = SF[18]*SF[23] + SF[17]*(SF[24] - 2*q0*q3);
SPP[16] = daz*SF[19] + daz*sq(q0) + daz*sq(q1) + daz*sq(q3);
SPP[17] = day*SF[19] + day*sq(q0) + day*sq(q1) + day*sq(q3);
SPP[18] = dax*SF[19] + dax*sq(q0) + dax*sq(q1) + dax*sq(q3);
SPP[19] = SF[16]*SF[23] - SF[17]*(2*q0*q2 + 2*q1*q3);
SPP[20] = SF[16]*SF[21] - SF[18]*SF[22];
SPP[21] = 2*q0*q2 + 2*q1*q3;
SPP[22] = SF[15];
if (inhibitMagStates) {
zeroRows(P,16,21);
zeroCols(P,16,21);
} else if (inhibitWindStates) {
zeroRows(P,22,23);
zeroCols(P,22,23);
}
nextP[0][0] = daxNoise*SQ[3] + SPP[5]*(P[0][0]*SPP[5] - P[1][0]*SPP[4] + P[9][0]*SPP[22] + P[12][0]*SPP[18] + P[2][0]*(2*q1*SF[3] - 2*q2*SF[4] - 2*q3*SF[5] + 2*q0*SF[9])) - SPP[4]*(P[0][1]*SPP[5] - P[1][1]*SPP[4] + P[9][1]*SPP[22] + P[12][1]*SPP[18] + P[2][1]*(2*q1*SF[3] - 2*q2*SF[4] - 2*q3*SF[5] + 2*q0*SF[9])) + SPP[8]*(P[0][2]*SPP[5] + P[2][2]*SPP[8] + P[9][2]*SPP[22] + P[12][2]*SPP[18] - P[1][2]*(2*q0*SF[6] - 2*q3*SF[7] - 2*q1*SF[10] + 2*q2*SF[12])) + SPP[22]*(P[0][9]*SPP[5] - P[1][9]*SPP[4] + P[9][9]*SPP[22] + P[12][9]*SPP[18] + P[2][9]*(2*q1*SF[3] - 2*q2*SF[4] - 2*q3*SF[5] + 2*q0*SF[9])) + SPP[18]*(P[0][12]*SPP[5] - P[1][12]*SPP[4] + P[9][12]*SPP[22] + P[12][12]*SPP[18] + P[2][12]*(2*q1*SF[3] - 2*q2*SF[4] - 2*q3*SF[5] + 2*q0*SF[9]));
nextP[0][1] = SPP[6]*(P[0][1]*SPP[5] - P[1][1]*SPP[4] + P[2][1]*SPP[8] + P[9][1]*SPP[22] + P[12][1]*SPP[18]) - SPP[2]*(P[0][0]*SPP[5] - P[1][0]*SPP[4] + P[2][0]*SPP[8] + P[9][0]*SPP[22] + P[12][0]*SPP[18]) + SPP[22]*(P[0][10]*SPP[5] - P[1][10]*SPP[4] + P[2][10]*SPP[8] + P[9][10]*SPP[22] + P[12][10]*SPP[18]) + SPP[17]*(P[0][13]*SPP[5] - P[1][13]*SPP[4] + P[2][13]*SPP[8] + P[9][13]*SPP[22] + P[12][13]*SPP[18]) - (2*q0*SF[5] - 2*q1*SF[4] - 2*q2*SF[3] + 2*q3*SF[9])*(P[0][2]*SPP[5] - P[1][2]*SPP[4] + P[2][2]*SPP[8] + P[9][2]*SPP[22] + P[12][2]*SPP[18]);
nextP[1][1] = dayNoise*SQ[3] - SPP[2]*(P[1][0]*SPP[6] - P[0][0]*SPP[2] - P[2][0]*SPP[9] + P[10][0]*SPP[22] + P[13][0]*SPP[17]) + SPP[6]*(P[1][1]*SPP[6] - P[0][1]*SPP[2] - P[2][1]*SPP[9] + P[10][1]*SPP[22] + P[13][1]*SPP[17]) - SPP[9]*(P[1][2]*SPP[6] - P[0][2]*SPP[2] - P[2][2]*SPP[9] + P[10][2]*SPP[22] + P[13][2]*SPP[17]) + SPP[22]*(P[1][10]*SPP[6] - P[0][10]*SPP[2] - P[2][10]*SPP[9] + P[10][10]*SPP[22] + P[13][10]*SPP[17]) + SPP[17]*(P[1][13]*SPP[6] - P[0][13]*SPP[2] - P[2][13]*SPP[9] + P[10][13]*SPP[22] + P[13][13]*SPP[17]);
nextP[0][2] = SPP[13]*(P[0][2]*SPP[5] - P[1][2]*SPP[4] + P[2][2]*SPP[8] + P[9][2]*SPP[22] + P[12][2]*SPP[18]) - SPP[3]*(P[0][1]*SPP[5] - P[1][1]*SPP[4] + P[2][1]*SPP[8] + P[9][1]*SPP[22] + P[12][1]*SPP[18]) + SPP[22]*(P[0][11]*SPP[5] - P[1][11]*SPP[4] + P[2][11]*SPP[8] + P[9][11]*SPP[22] + P[12][11]*SPP[18]) + SPP[16]*(P[0][14]*SPP[5] - P[1][14]*SPP[4] + P[2][14]*SPP[8] + P[9][14]*SPP[22] + P[12][14]*SPP[18]) + (2*q2*SF[8] - 2*q0*SF[11] - 2*q1*SF[14] + 2*q3*SF[13])*(P[0][0]*SPP[5] - P[1][0]*SPP[4] + P[2][0]*SPP[8] + P[9][0]*SPP[22] + P[12][0]*SPP[18]);
nextP[1][2] = SPP[13]*(P[1][2]*SPP[6] - P[0][2]*SPP[2] - P[2][2]*SPP[9] + P[10][2]*SPP[22] + P[13][2]*SPP[17]) - SPP[3]*(P[1][1]*SPP[6] - P[0][1]*SPP[2] - P[2][1]*SPP[9] + P[10][1]*SPP[22] + P[13][1]*SPP[17]) + SPP[22]*(P[1][11]*SPP[6] - P[0][11]*SPP[2] - P[2][11]*SPP[9] + P[10][11]*SPP[22] + P[13][11]*SPP[17]) + SPP[16]*(P[1][14]*SPP[6] - P[0][14]*SPP[2] - P[2][14]*SPP[9] + P[10][14]*SPP[22] + P[13][14]*SPP[17]) + (2*q2*SF[8] - 2*q0*SF[11] - 2*q1*SF[14] + 2*q3*SF[13])*(P[1][0]*SPP[6] - P[0][0]*SPP[2] - P[2][0]*SPP[9] + P[10][0]*SPP[22] + P[13][0]*SPP[17]);
nextP[2][2] = dazNoise*SQ[3] - SPP[3]*(P[0][1]*SPP[14] - P[1][1]*SPP[3] + P[2][1]*SPP[13] + P[11][1]*SPP[22] + P[14][1]*SPP[16]) + SPP[14]*(P[0][0]*SPP[14] - P[1][0]*SPP[3] + P[2][0]*SPP[13] + P[11][0]*SPP[22] + P[14][0]*SPP[16]) + SPP[13]*(P[0][2]*SPP[14] - P[1][2]*SPP[3] + P[2][2]*SPP[13] + P[11][2]*SPP[22] + P[14][2]*SPP[16]) + SPP[22]*(P[0][11]*SPP[14] - P[1][11]*SPP[3] + P[2][11]*SPP[13] + P[11][11]*SPP[22] + P[14][11]*SPP[16]) + SPP[16]*(P[0][14]*SPP[14] - P[1][14]*SPP[3] + P[2][14]*SPP[13] + P[11][14]*SPP[22] + P[14][14]*SPP[16]);
nextP[0][3] = P[0][3]*SPP[5] - P[1][3]*SPP[4] + P[2][3]*SPP[8] + P[9][3]*SPP[22] + P[12][3]*SPP[18] + SPP[1]*(P[0][0]*SPP[5] - P[1][0]*SPP[4] + P[2][0]*SPP[8] + P[9][0]*SPP[22] + P[12][0]*SPP[18]) + SPP[15]*(P[0][2]*SPP[5] - P[1][2]*SPP[4] + P[2][2]*SPP[8] + P[9][2]*SPP[22] + P[12][2]*SPP[18]) - SPP[21]*(P[0][15]*SPP[5] - P[1][15]*SPP[4] + P[2][15]*SPP[8] + P[9][15]*SPP[22] + P[12][15]*SPP[18]) + (SF[16]*SF[23] - SF[17]*SPP[21])*(P[0][1]*SPP[5] - P[1][1]*SPP[4] + P[2][1]*SPP[8] + P[9][1]*SPP[22] + P[12][1]*SPP[18]);
nextP[1][3] = P[1][3]*SPP[6] - P[0][3]*SPP[2] - P[2][3]*SPP[9] + P[10][3]*SPP[22] + P[13][3]*SPP[17] + SPP[1]*(P[1][0]*SPP[6] - P[0][0]*SPP[2] - P[2][0]*SPP[9] + P[10][0]*SPP[22] + P[13][0]*SPP[17]) + SPP[15]*(P[1][2]*SPP[6] - P[0][2]*SPP[2] - P[2][2]*SPP[9] + P[10][2]*SPP[22] + P[13][2]*SPP[17]) - SPP[21]*(P[1][15]*SPP[6] - P[0][15]*SPP[2] - P[2][15]*SPP[9] + P[10][15]*SPP[22] + P[13][15]*SPP[17]) + (SF[16]*SF[23] - SF[17]*SPP[21])*(P[1][1]*SPP[6] - P[0][1]*SPP[2] - P[2][1]*SPP[9] + P[10][1]*SPP[22] + P[13][1]*SPP[17]);
nextP[2][3] = P[0][3]*SPP[14] - P[1][3]*SPP[3] + P[2][3]*SPP[13] + P[11][3]*SPP[22] + P[14][3]*SPP[16] + SPP[1]*(P[0][0]*SPP[14] - P[1][0]*SPP[3] + P[2][0]*SPP[13] + P[11][0]*SPP[22] + P[14][0]*SPP[16]) + SPP[15]*(P[0][2]*SPP[14] - P[1][2]*SPP[3] + P[2][2]*SPP[13] + P[11][2]*SPP[22] + P[14][2]*SPP[16]) - SPP[21]*(P[0][15]*SPP[14] - P[1][15]*SPP[3] + P[2][15]*SPP[13] + P[11][15]*SPP[22] + P[14][15]*SPP[16]) + (SF[16]*SF[23] - SF[17]*SPP[21])*(P[0][1]*SPP[14] - P[1][1]*SPP[3] + P[2][1]*SPP[13] + P[11][1]*SPP[22] + P[14][1]*SPP[16]);
nextP[3][3] = P[3][3] + P[0][3]*SPP[1] + P[1][3]*SPP[19] + P[2][3]*SPP[15] - P[15][3]*SPP[21] + dvyNoise*sq(SQ[6] - 2*q0*q3) + dvzNoise*sq(SQ[5] + 2*q0*q2) + SPP[1]*(P[3][0] + P[0][0]*SPP[1] + P[1][0]*SPP[19] + P[2][0]*SPP[15] - P[15][0]*SPP[21]) + SPP[19]*(P[3][1] + P[0][1]*SPP[1] + P[1][1]*SPP[19] + P[2][1]*SPP[15] - P[15][1]*SPP[21]) + SPP[15]*(P[3][2] + P[0][2]*SPP[1] + P[1][2]*SPP[19] + P[2][2]*SPP[15] - P[15][2]*SPP[21]) - SPP[21]*(P[3][15] + P[0][15]*SPP[1] + P[2][15]*SPP[15] - P[15][15]*SPP[21] + P[1][15]*(SF[16]*SF[23] - SF[17]*SPP[21])) + dvxNoise*sq(SG[1] + SG[2] - SG[3] - SQ[7]);
nextP[0][4] = P[0][4]*SPP[5] - P[1][4]*SPP[4] + P[2][4]*SPP[8] + P[9][4]*SPP[22] + P[12][4]*SPP[18] + SF[22]*(P[0][15]*SPP[5] - P[1][15]*SPP[4] + P[2][15]*SPP[8] + P[9][15]*SPP[22] + P[12][15]*SPP[18]) + SPP[12]*(P[0][1]*SPP[5] - P[1][1]*SPP[4] + P[2][1]*SPP[8] + P[9][1]*SPP[22] + P[12][1]*SPP[18]) + SPP[20]*(P[0][0]*SPP[5] - P[1][0]*SPP[4] + P[2][0]*SPP[8] + P[9][0]*SPP[22] + P[12][0]*SPP[18]) + SPP[11]*(P[0][2]*SPP[5] - P[1][2]*SPP[4] + P[2][2]*SPP[8] + P[9][2]*SPP[22] + P[12][2]*SPP[18]);
nextP[1][4] = P[1][4]*SPP[6] - P[0][4]*SPP[2] - P[2][4]*SPP[9] + P[10][4]*SPP[22] + P[13][4]*SPP[17] + SF[22]*(P[1][15]*SPP[6] - P[0][15]*SPP[2] - P[2][15]*SPP[9] + P[10][15]*SPP[22] + P[13][15]*SPP[17]) + SPP[12]*(P[1][1]*SPP[6] - P[0][1]*SPP[2] - P[2][1]*SPP[9] + P[10][1]*SPP[22] + P[13][1]*SPP[17]) + SPP[20]*(P[1][0]*SPP[6] - P[0][0]*SPP[2] - P[2][0]*SPP[9] + P[10][0]*SPP[22] + P[13][0]*SPP[17]) + SPP[11]*(P[1][2]*SPP[6] - P[0][2]*SPP[2] - P[2][2]*SPP[9] + P[10][2]*SPP[22] + P[13][2]*SPP[17]);
nextP[2][4] = P[0][4]*SPP[14] - P[1][4]*SPP[3] + P[2][4]*SPP[13] + P[11][4]*SPP[22] + P[14][4]*SPP[16] + SF[22]*(P[0][15]*SPP[14] - P[1][15]*SPP[3] + P[2][15]*SPP[13] + P[11][15]*SPP[22] + P[14][15]*SPP[16]) + SPP[12]*(P[0][1]*SPP[14] - P[1][1]*SPP[3] + P[2][1]*SPP[13] + P[11][1]*SPP[22] + P[14][1]*SPP[16]) + SPP[20]*(P[0][0]*SPP[14] - P[1][0]*SPP[3] + P[2][0]*SPP[13] + P[11][0]*SPP[22] + P[14][0]*SPP[16]) + SPP[11]*(P[0][2]*SPP[14] - P[1][2]*SPP[3] + P[2][2]*SPP[13] + P[11][2]*SPP[22] + P[14][2]*SPP[16]);
nextP[3][4] = P[3][4] + SQ[2] + P[0][4]*SPP[1] + P[1][4]*SPP[19] + P[2][4]*SPP[15] - P[15][4]*SPP[21] + SF[22]*(P[3][15] + P[0][15]*SPP[1] + P[1][15]*SPP[19] + P[2][15]*SPP[15] - P[15][15]*SPP[21]) + SPP[12]*(P[3][1] + P[0][1]*SPP[1] + P[1][1]*SPP[19] + P[2][1]*SPP[15] - P[15][1]*SPP[21]) + SPP[20]*(P[3][0] + P[0][0]*SPP[1] + P[1][0]*SPP[19] + P[2][0]*SPP[15] - P[15][0]*SPP[21]) + SPP[11]*(P[3][2] + P[0][2]*SPP[1] + P[1][2]*SPP[19] + P[2][2]*SPP[15] - P[15][2]*SPP[21]);
nextP[4][4] = P[4][4] + P[15][4]*SF[22] + P[0][4]*SPP[20] + P[1][4]*SPP[12] + P[2][4]*SPP[11] + dvxNoise*sq(SQ[6] + 2*q0*q3) + dvzNoise*sq(SQ[4] - 2*q0*q1) + SF[22]*(P[4][15] + P[15][15]*SF[22] + P[0][15]*SPP[20] + P[1][15]*SPP[12] + P[2][15]*SPP[11]) + SPP[12]*(P[4][1] + P[15][1]*SF[22] + P[0][1]*SPP[20] + P[1][1]*SPP[12] + P[2][1]*SPP[11]) + SPP[20]*(P[4][0] + P[15][0]*SF[22] + P[0][0]*SPP[20] + P[1][0]*SPP[12] + P[2][0]*SPP[11]) + SPP[11]*(P[4][2] + P[15][2]*SF[22] + P[0][2]*SPP[20] + P[1][2]*SPP[12] + P[2][2]*SPP[11]) + dvyNoise*sq(SG[1] - SG[2] + SG[3] - SQ[7]);
nextP[0][5] = P[0][5]*SPP[5] - P[1][5]*SPP[4] + P[2][5]*SPP[8] + P[9][5]*SPP[22] + P[12][5]*SPP[18] + SF[20]*(P[0][15]*SPP[5] - P[1][15]*SPP[4] + P[2][15]*SPP[8] + P[9][15]*SPP[22] + P[12][15]*SPP[18]) - SPP[7]*(P[0][0]*SPP[5] - P[1][0]*SPP[4] + P[2][0]*SPP[8] + P[9][0]*SPP[22] + P[12][0]*SPP[18]) + SPP[0]*(P[0][2]*SPP[5] - P[1][2]*SPP[4] + P[2][2]*SPP[8] + P[9][2]*SPP[22] + P[12][2]*SPP[18]) + SPP[10]*(P[0][1]*SPP[5] - P[1][1]*SPP[4] + P[2][1]*SPP[8] + P[9][1]*SPP[22] + P[12][1]*SPP[18]);
nextP[1][5] = P[1][5]*SPP[6] - P[0][5]*SPP[2] - P[2][5]*SPP[9] + P[10][5]*SPP[22] + P[13][5]*SPP[17] + SF[20]*(P[1][15]*SPP[6] - P[0][15]*SPP[2] - P[2][15]*SPP[9] + P[10][15]*SPP[22] + P[13][15]*SPP[17]) - SPP[7]*(P[1][0]*SPP[6] - P[0][0]*SPP[2] - P[2][0]*SPP[9] + P[10][0]*SPP[22] + P[13][0]*SPP[17]) + SPP[0]*(P[1][2]*SPP[6] - P[0][2]*SPP[2] - P[2][2]*SPP[9] + P[10][2]*SPP[22] + P[13][2]*SPP[17]) + SPP[10]*(P[1][1]*SPP[6] - P[0][1]*SPP[2] - P[2][1]*SPP[9] + P[10][1]*SPP[22] + P[13][1]*SPP[17]);
nextP[2][5] = P[0][5]*SPP[14] - P[1][5]*SPP[3] + P[2][5]*SPP[13] + P[11][5]*SPP[22] + P[14][5]*SPP[16] + SF[20]*(P[0][15]*SPP[14] - P[1][15]*SPP[3] + P[2][15]*SPP[13] + P[11][15]*SPP[22] + P[14][15]*SPP[16]) - SPP[7]*(P[0][0]*SPP[14] - P[1][0]*SPP[3] + P[2][0]*SPP[13] + P[11][0]*SPP[22] + P[14][0]*SPP[16]) + SPP[0]*(P[0][2]*SPP[14] - P[1][2]*SPP[3] + P[2][2]*SPP[13] + P[11][2]*SPP[22] + P[14][2]*SPP[16]) + SPP[10]*(P[0][1]*SPP[14] - P[1][1]*SPP[3] + P[2][1]*SPP[13] + P[11][1]*SPP[22] + P[14][1]*SPP[16]);
nextP[3][5] = P[3][5] + SQ[1] + P[0][5]*SPP[1] + P[1][5]*SPP[19] + P[2][5]*SPP[15] - P[15][5]*SPP[21] + SF[20]*(P[3][15] + P[0][15]*SPP[1] + P[1][15]*SPP[19] + P[2][15]*SPP[15] - P[15][15]*SPP[21]) - SPP[7]*(P[3][0] + P[0][0]*SPP[1] + P[1][0]*SPP[19] + P[2][0]*SPP[15] - P[15][0]*SPP[21]) + SPP[0]*(P[3][2] + P[0][2]*SPP[1] + P[1][2]*SPP[19] + P[2][2]*SPP[15] - P[15][2]*SPP[21]) + SPP[10]*(P[3][1] + P[0][1]*SPP[1] + P[1][1]*SPP[19] + P[2][1]*SPP[15] - P[15][1]*SPP[21]);
nextP[4][5] = P[4][5] + SQ[0] + P[15][5]*SF[22] + P[0][5]*SPP[20] + P[1][5]*SPP[12] + P[2][5]*SPP[11] + SF[20]*(P[4][15] + P[15][15]*SF[22] + P[0][15]*SPP[20] + P[1][15]*SPP[12] + P[2][15]*SPP[11]) - SPP[7]*(P[4][0] + P[15][0]*SF[22] + P[0][0]*SPP[20] + P[1][0]*SPP[12] + P[2][0]*SPP[11]) + SPP[0]*(P[4][2] + P[15][2]*SF[22] + P[0][2]*SPP[20] + P[1][2]*SPP[12] + P[2][2]*SPP[11]) + SPP[10]*(P[4][1] + P[15][1]*SF[22] + P[0][1]*SPP[20] + P[1][1]*SPP[12] + P[2][1]*SPP[11]);
nextP[5][5] = P[5][5] + P[15][5]*SF[20] - P[0][5]*SPP[7] + P[1][5]*SPP[10] + P[2][5]*SPP[0] + dvxNoise*sq(SQ[5] - 2*q0*q2) + dvyNoise*sq(SQ[4] + 2*q0*q1) + SF[20]*(P[5][15] + P[15][15]*SF[20] - P[0][15]*SPP[7] + P[1][15]*SPP[10] + P[2][15]*SPP[0]) - SPP[7]*(P[5][0] + P[15][0]*SF[20] - P[0][0]*SPP[7] + P[1][0]*SPP[10] + P[2][0]*SPP[0]) + SPP[0]*(P[5][2] + P[15][2]*SF[20] - P[0][2]*SPP[7] + P[1][2]*SPP[10] + P[2][2]*SPP[0]) + SPP[10]*(P[5][1] + P[15][1]*SF[20] - P[0][1]*SPP[7] + P[1][1]*SPP[10] + P[2][1]*SPP[0]) + dvzNoise*sq(SG[1] - SG[2] - SG[3] + SQ[7]);
nextP[0][6] = P[0][6]*SPP[5] - P[1][6]*SPP[4] + P[2][6]*SPP[8] + P[9][6]*SPP[22] + P[12][6]*SPP[18] + dt*(P[0][3]*SPP[5] - P[1][3]*SPP[4] + P[2][3]*SPP[8] + P[9][3]*SPP[22] + P[12][3]*SPP[18]);
nextP[1][6] = P[1][6]*SPP[6] - P[0][6]*SPP[2] - P[2][6]*SPP[9] + P[10][6]*SPP[22] + P[13][6]*SPP[17] + dt*(P[1][3]*SPP[6] - P[0][3]*SPP[2] - P[2][3]*SPP[9] + P[10][3]*SPP[22] + P[13][3]*SPP[17]);
nextP[2][6] = P[0][6]*SPP[14] - P[1][6]*SPP[3] + P[2][6]*SPP[13] + P[11][6]*SPP[22] + P[14][6]*SPP[16] + dt*(P[0][3]*SPP[14] - P[1][3]*SPP[3] + P[2][3]*SPP[13] + P[11][3]*SPP[22] + P[14][3]*SPP[16]);
nextP[3][6] = P[3][6] + P[0][6]*SPP[1] + P[1][6]*SPP[19] + P[2][6]*SPP[15] - P[15][6]*SPP[21] + dt*(P[3][3] + P[0][3]*SPP[1] + P[1][3]*SPP[19] + P[2][3]*SPP[15] - P[15][3]*SPP[21]);
nextP[4][6] = P[4][6] + P[15][6]*SF[22] + P[0][6]*SPP[20] + P[1][6]*SPP[12] + P[2][6]*SPP[11] + dt*(P[4][3] + P[15][3]*SF[22] + P[0][3]*SPP[20] + P[1][3]*SPP[12] + P[2][3]*SPP[11]);
nextP[5][6] = P[5][6] + P[15][6]*SF[20] - P[0][6]*SPP[7] + P[1][6]*SPP[10] + P[2][6]*SPP[0] + dt*(P[5][3] + P[15][3]*SF[20] - P[0][3]*SPP[7] + P[1][3]*SPP[10] + P[2][3]*SPP[0]);
nextP[6][6] = P[6][6] + P[3][6]*dt + dt*(P[6][3] + P[3][3]*dt);
nextP[0][7] = P[0][7]*SPP[5] - P[1][7]*SPP[4] + P[2][7]*SPP[8] + P[9][7]*SPP[22] + P[12][7]*SPP[18] + dt*(P[0][4]*SPP[5] - P[1][4]*SPP[4] + P[2][4]*SPP[8] + P[9][4]*SPP[22] + P[12][4]*SPP[18]);
nextP[1][7] = P[1][7]*SPP[6] - P[0][7]*SPP[2] - P[2][7]*SPP[9] + P[10][7]*SPP[22] + P[13][7]*SPP[17] + dt*(P[1][4]*SPP[6] - P[0][4]*SPP[2] - P[2][4]*SPP[9] + P[10][4]*SPP[22] + P[13][4]*SPP[17]);
nextP[2][7] = P[0][7]*SPP[14] - P[1][7]*SPP[3] + P[2][7]*SPP[13] + P[11][7]*SPP[22] + P[14][7]*SPP[16] + dt*(P[0][4]*SPP[14] - P[1][4]*SPP[3] + P[2][4]*SPP[13] + P[11][4]*SPP[22] + P[14][4]*SPP[16]);
nextP[3][7] = P[3][7] + P[0][7]*SPP[1] + P[1][7]*SPP[19] + P[2][7]*SPP[15] - P[15][7]*SPP[21] + dt*(P[3][4] + P[0][4]*SPP[1] + P[1][4]*SPP[19] + P[2][4]*SPP[15] - P[15][4]*SPP[21]);
nextP[4][7] = P[4][7] + P[15][7]*SF[22] + P[0][7]*SPP[20] + P[1][7]*SPP[12] + P[2][7]*SPP[11] + dt*(P[4][4] + P[15][4]*SF[22] + P[0][4]*SPP[20] + P[1][4]*SPP[12] + P[2][4]*SPP[11]);
nextP[5][7] = P[5][7] + P[15][7]*SF[20] - P[0][7]*SPP[7] + P[1][7]*SPP[10] + P[2][7]*SPP[0] + dt*(P[5][4] + P[15][4]*SF[20] - P[0][4]*SPP[7] + P[1][4]*SPP[10] + P[2][4]*SPP[0]);
nextP[6][7] = P[6][7] + P[3][7]*dt + dt*(P[6][4] + P[3][4]*dt);
nextP[7][7] = P[7][7] + P[4][7]*dt + dt*(P[7][4] + P[4][4]*dt);
nextP[0][8] = P[0][8]*SPP[5] - P[1][8]*SPP[4] + P[2][8]*SPP[8] + P[9][8]*SPP[22] + P[12][8]*SPP[18] + dt*(P[0][5]*SPP[5] - P[1][5]*SPP[4] + P[2][5]*SPP[8] + P[9][5]*SPP[22] + P[12][5]*SPP[18]);
nextP[1][8] = P[1][8]*SPP[6] - P[0][8]*SPP[2] - P[2][8]*SPP[9] + P[10][8]*SPP[22] + P[13][8]*SPP[17] + dt*(P[1][5]*SPP[6] - P[0][5]*SPP[2] - P[2][5]*SPP[9] + P[10][5]*SPP[22] + P[13][5]*SPP[17]);
nextP[2][8] = P[0][8]*SPP[14] - P[1][8]*SPP[3] + P[2][8]*SPP[13] + P[11][8]*SPP[22] + P[14][8]*SPP[16] + dt*(P[0][5]*SPP[14] - P[1][5]*SPP[3] + P[2][5]*SPP[13] + P[11][5]*SPP[22] + P[14][5]*SPP[16]);
nextP[3][8] = P[3][8] + P[0][8]*SPP[1] + P[1][8]*SPP[19] + P[2][8]*SPP[15] - P[15][8]*SPP[21] + dt*(P[3][5] + P[0][5]*SPP[1] + P[1][5]*SPP[19] + P[2][5]*SPP[15] - P[15][5]*SPP[21]);
nextP[4][8] = P[4][8] + P[15][8]*SF[22] + P[0][8]*SPP[20] + P[1][8]*SPP[12] + P[2][8]*SPP[11] + dt*(P[4][5] + P[15][5]*SF[22] + P[0][5]*SPP[20] + P[1][5]*SPP[12] + P[2][5]*SPP[11]);
nextP[5][8] = P[5][8] + P[15][8]*SF[20] - P[0][8]*SPP[7] + P[1][8]*SPP[10] + P[2][8]*SPP[0] + dt*(P[5][5] + P[15][5]*SF[20] - P[0][5]*SPP[7] + P[1][5]*SPP[10] + P[2][5]*SPP[0]);
nextP[6][8] = P[6][8] + P[3][8]*dt + dt*(P[6][5] + P[3][5]*dt);
nextP[7][8] = P[7][8] + P[4][8]*dt + dt*(P[7][5] + P[4][5]*dt);
nextP[8][8] = P[8][8] + P[5][8]*dt + dt*(P[8][5] + P[5][5]*dt);
nextP[0][9] = P[0][9]*SPP[5] - P[1][9]*SPP[4] + P[2][9]*SPP[8] + P[9][9]*SPP[22] + P[12][9]*SPP[18];
nextP[1][9] = P[1][9]*SPP[6] - P[0][9]*SPP[2] - P[2][9]*SPP[9] + P[10][9]*SPP[22] + P[13][9]*SPP[17];
nextP[2][9] = P[0][9]*SPP[14] - P[1][9]*SPP[3] + P[2][9]*SPP[13] + P[11][9]*SPP[22] + P[14][9]*SPP[16];
nextP[3][9] = P[3][9] + P[0][9]*SPP[1] + P[1][9]*SPP[19] + P[2][9]*SPP[15] - P[15][9]*SPP[21];
nextP[4][9] = P[4][9] + P[15][9]*SF[22] + P[0][9]*SPP[20] + P[1][9]*SPP[12] + P[2][9]*SPP[11];
nextP[5][9] = P[5][9] + P[15][9]*SF[20] - P[0][9]*SPP[7] + P[1][9]*SPP[10] + P[2][9]*SPP[0];
nextP[6][9] = P[6][9] + P[3][9]*dt;
nextP[7][9] = P[7][9] + P[4][9]*dt;
nextP[8][9] = P[8][9] + P[5][9]*dt;
nextP[9][9] = P[9][9];
nextP[0][10] = P[0][10]*SPP[5] - P[1][10]*SPP[4] + P[2][10]*SPP[8] + P[9][10]*SPP[22] + P[12][10]*SPP[18];
nextP[1][10] = P[1][10]*SPP[6] - P[0][10]*SPP[2] - P[2][10]*SPP[9] + P[10][10]*SPP[22] + P[13][10]*SPP[17];
nextP[2][10] = P[0][10]*SPP[14] - P[1][10]*SPP[3] + P[2][10]*SPP[13] + P[11][10]*SPP[22] + P[14][10]*SPP[16];
nextP[3][10] = P[3][10] + P[0][10]*SPP[1] + P[1][10]*SPP[19] + P[2][10]*SPP[15] - P[15][10]*SPP[21];
nextP[4][10] = P[4][10] + P[15][10]*SF[22] + P[0][10]*SPP[20] + P[1][10]*SPP[12] + P[2][10]*SPP[11];
nextP[5][10] = P[5][10] + P[15][10]*SF[20] - P[0][10]*SPP[7] + P[1][10]*SPP[10] + P[2][10]*SPP[0];
nextP[6][10] = P[6][10] + P[3][10]*dt;
nextP[7][10] = P[7][10] + P[4][10]*dt;
nextP[8][10] = P[8][10] + P[5][10]*dt;
nextP[9][10] = P[9][10];
nextP[10][10] = P[10][10];
nextP[0][11] = P[0][11]*SPP[5] - P[1][11]*SPP[4] + P[2][11]*SPP[8] + P[9][11]*SPP[22] + P[12][11]*SPP[18];
nextP[1][11] = P[1][11]*SPP[6] - P[0][11]*SPP[2] - P[2][11]*SPP[9] + P[10][11]*SPP[22] + P[13][11]*SPP[17];
nextP[2][11] = P[0][11]*SPP[14] - P[1][11]*SPP[3] + P[2][11]*SPP[13] + P[11][11]*SPP[22] + P[14][11]*SPP[16];
nextP[3][11] = P[3][11] + P[0][11]*SPP[1] + P[1][11]*SPP[19] + P[2][11]*SPP[15] - P[15][11]*SPP[21];
nextP[4][11] = P[4][11] + P[15][11]*SF[22] + P[0][11]*SPP[20] + P[1][11]*SPP[12] + P[2][11]*SPP[11];
nextP[5][11] = P[5][11] + P[15][11]*SF[20] - P[0][11]*SPP[7] + P[1][11]*SPP[10] + P[2][11]*SPP[0];
nextP[6][11] = P[6][11] + P[3][11]*dt;
nextP[7][11] = P[7][11] + P[4][11]*dt;
nextP[8][11] = P[8][11] + P[5][11]*dt;
nextP[9][11] = P[9][11];
nextP[10][11] = P[10][11];
nextP[11][11] = P[11][11];
nextP[0][12] = P[0][12]*SPP[5] - P[1][12]*SPP[4] + P[2][12]*SPP[8] + P[9][12]*SPP[22] + P[12][12]*SPP[18];
nextP[1][12] = P[1][12]*SPP[6] - P[0][12]*SPP[2] - P[2][12]*SPP[9] + P[10][12]*SPP[22] + P[13][12]*SPP[17];
nextP[2][12] = P[0][12]*SPP[14] - P[1][12]*SPP[3] + P[2][12]*SPP[13] + P[11][12]*SPP[22] + P[14][12]*SPP[16];
nextP[3][12] = P[3][12] + P[0][12]*SPP[1] + P[1][12]*SPP[19] + P[2][12]*SPP[15] - P[15][12]*SPP[21];
nextP[4][12] = P[4][12] + P[15][12]*SF[22] + P[0][12]*SPP[20] + P[1][12]*SPP[12] + P[2][12]*SPP[11];
nextP[5][12] = P[5][12] + P[15][12]*SF[20] - P[0][12]*SPP[7] + P[1][12]*SPP[10] + P[2][12]*SPP[0];
nextP[6][12] = P[6][12] + P[3][12]*dt;
nextP[7][12] = P[7][12] + P[4][12]*dt;
nextP[8][12] = P[8][12] + P[5][12]*dt;
nextP[9][12] = P[9][12];
nextP[10][12] = P[10][12];
nextP[11][12] = P[11][12];
nextP[12][12] = P[12][12];
nextP[0][13] = P[0][13]*SPP[5] - P[1][13]*SPP[4] + P[2][13]*SPP[8] + P[9][13]*SPP[22] + P[12][13]*SPP[18];
nextP[1][13] = P[1][13]*SPP[6] - P[0][13]*SPP[2] - P[2][13]*SPP[9] + P[10][13]*SPP[22] + P[13][13]*SPP[17];
nextP[2][13] = P[0][13]*SPP[14] - P[1][13]*SPP[3] + P[2][13]*SPP[13] + P[11][13]*SPP[22] + P[14][13]*SPP[16];
nextP[3][13] = P[3][13] + P[0][13]*SPP[1] + P[1][13]*SPP[19] + P[2][13]*SPP[15] - P[15][13]*SPP[21];
nextP[4][13] = P[4][13] + P[15][13]*SF[22] + P[0][13]*SPP[20] + P[1][13]*SPP[12] + P[2][13]*SPP[11];
nextP[5][13] = P[5][13] + P[15][13]*SF[20] - P[0][13]*SPP[7] + P[1][13]*SPP[10] + P[2][13]*SPP[0];
nextP[6][13] = P[6][13] + P[3][13]*dt;
nextP[7][13] = P[7][13] + P[4][13]*dt;
nextP[8][13] = P[8][13] + P[5][13]*dt;
nextP[9][13] = P[9][13];
nextP[10][13] = P[10][13];
nextP[11][13] = P[11][13];
nextP[12][13] = P[12][13];
nextP[13][13] = P[13][13];
nextP[0][14] = P[0][14]*SPP[5] - P[1][14]*SPP[4] + P[2][14]*SPP[8] + P[9][14]*SPP[22] + P[12][14]*SPP[18];
nextP[1][14] = P[1][14]*SPP[6] - P[0][14]*SPP[2] - P[2][14]*SPP[9] + P[10][14]*SPP[22] + P[13][14]*SPP[17];
nextP[2][14] = P[0][14]*SPP[14] - P[1][14]*SPP[3] + P[2][14]*SPP[13] + P[11][14]*SPP[22] + P[14][14]*SPP[16];
nextP[3][14] = P[3][14] + P[0][14]*SPP[1] + P[1][14]*SPP[19] + P[2][14]*SPP[15] - P[15][14]*SPP[21];
nextP[4][14] = P[4][14] + P[15][14]*SF[22] + P[0][14]*SPP[20] + P[1][14]*SPP[12] + P[2][14]*SPP[11];
nextP[5][14] = P[5][14] + P[15][14]*SF[20] - P[0][14]*SPP[7] + P[1][14]*SPP[10] + P[2][14]*SPP[0];
nextP[6][14] = P[6][14] + P[3][14]*dt;
nextP[7][14] = P[7][14] + P[4][14]*dt;
nextP[8][14] = P[8][14] + P[5][14]*dt;
nextP[9][14] = P[9][14];
nextP[10][14] = P[10][14];
nextP[11][14] = P[11][14];
nextP[12][14] = P[12][14];
nextP[13][14] = P[13][14];
nextP[14][14] = P[14][14];
nextP[0][15] = P[0][15]*SPP[5] - P[1][15]*SPP[4] + P[2][15]*SPP[8] + P[9][15]*SPP[22] + P[12][15]*SPP[18];
nextP[1][15] = P[1][15]*SPP[6] - P[0][15]*SPP[2] - P[2][15]*SPP[9] + P[10][15]*SPP[22] + P[13][15]*SPP[17];
nextP[2][15] = P[0][15]*SPP[14] - P[1][15]*SPP[3] + P[2][15]*SPP[13] + P[11][15]*SPP[22] + P[14][15]*SPP[16];
nextP[3][15] = P[3][15] + P[0][15]*SPP[1] + P[1][15]*SPP[19] + P[2][15]*SPP[15] - P[15][15]*SPP[21];
nextP[4][15] = P[4][15] + P[15][15]*SF[22] + P[0][15]*SPP[20] + P[1][15]*SPP[12] + P[2][15]*SPP[11];
nextP[5][15] = P[5][15] + P[15][15]*SF[20] - P[0][15]*SPP[7] + P[1][15]*SPP[10] + P[2][15]*SPP[0];
nextP[6][15] = P[6][15] + P[3][15]*dt;
nextP[7][15] = P[7][15] + P[4][15]*dt;
nextP[8][15] = P[8][15] + P[5][15]*dt;
nextP[9][15] = P[9][15];
nextP[10][15] = P[10][15];
nextP[11][15] = P[11][15];
nextP[12][15] = P[12][15];
nextP[13][15] = P[13][15];
nextP[14][15] = P[14][15];
nextP[15][15] = P[15][15];
if (stateIndexLim > 15) {
nextP[0][16] = P[0][16]*SPP[5] - P[1][16]*SPP[4] + P[2][16]*SPP[8] + P[9][16]*SPP[22] + P[12][16]*SPP[18];
nextP[1][16] = P[1][16]*SPP[6] - P[0][16]*SPP[2] - P[2][16]*SPP[9] + P[10][16]*SPP[22] + P[13][16]*SPP[17];
nextP[2][16] = P[0][16]*SPP[14] - P[1][16]*SPP[3] + P[2][16]*SPP[13] + P[11][16]*SPP[22] + P[14][16]*SPP[16];
nextP[3][16] = P[3][16] + P[0][16]*SPP[1] + P[1][16]*SPP[19] + P[2][16]*SPP[15] - P[15][16]*SPP[21];
nextP[4][16] = P[4][16] + P[15][16]*SF[22] + P[0][16]*SPP[20] + P[1][16]*SPP[12] + P[2][16]*SPP[11];
nextP[5][16] = P[5][16] + P[15][16]*SF[20] - P[0][16]*SPP[7] + P[1][16]*SPP[10] + P[2][16]*SPP[0];
nextP[6][16] = P[6][16] + P[3][16]*dt;
nextP[7][16] = P[7][16] + P[4][16]*dt;
nextP[8][16] = P[8][16] + P[5][16]*dt;
nextP[9][16] = P[9][16];
nextP[10][16] = P[10][16];
nextP[11][16] = P[11][16];
nextP[12][16] = P[12][16];
nextP[13][16] = P[13][16];
nextP[14][16] = P[14][16];
nextP[15][16] = P[15][16];
nextP[16][16] = P[16][16];
nextP[0][17] = P[0][17]*SPP[5] - P[1][17]*SPP[4] + P[2][17]*SPP[8] + P[9][17]*SPP[22] + P[12][17]*SPP[18];
nextP[1][17] = P[1][17]*SPP[6] - P[0][17]*SPP[2] - P[2][17]*SPP[9] + P[10][17]*SPP[22] + P[13][17]*SPP[17];
nextP[2][17] = P[0][17]*SPP[14] - P[1][17]*SPP[3] + P[2][17]*SPP[13] + P[11][17]*SPP[22] + P[14][17]*SPP[16];
nextP[3][17] = P[3][17] + P[0][17]*SPP[1] + P[1][17]*SPP[19] + P[2][17]*SPP[15] - P[15][17]*SPP[21];
nextP[4][17] = P[4][17] + P[15][17]*SF[22] + P[0][17]*SPP[20] + P[1][17]*SPP[12] + P[2][17]*SPP[11];
nextP[5][17] = P[5][17] + P[15][17]*SF[20] - P[0][17]*SPP[7] + P[1][17]*SPP[10] + P[2][17]*SPP[0];
nextP[6][17] = P[6][17] + P[3][17]*dt;
nextP[7][17] = P[7][17] + P[4][17]*dt;
nextP[8][17] = P[8][17] + P[5][17]*dt;
nextP[9][17] = P[9][17];
nextP[10][17] = P[10][17];
nextP[11][17] = P[11][17];
nextP[12][17] = P[12][17];
nextP[13][17] = P[13][17];
nextP[14][17] = P[14][17];
nextP[15][17] = P[15][17];
nextP[16][17] = P[16][17];
nextP[17][17] = P[17][17];
nextP[0][18] = P[0][18]*SPP[5] - P[1][18]*SPP[4] + P[2][18]*SPP[8] + P[9][18]*SPP[22] + P[12][18]*SPP[18];
nextP[1][18] = P[1][18]*SPP[6] - P[0][18]*SPP[2] - P[2][18]*SPP[9] + P[10][18]*SPP[22] + P[13][18]*SPP[17];
nextP[2][18] = P[0][18]*SPP[14] - P[1][18]*SPP[3] + P[2][18]*SPP[13] + P[11][18]*SPP[22] + P[14][18]*SPP[16];
nextP[3][18] = P[3][18] + P[0][18]*SPP[1] + P[1][18]*SPP[19] + P[2][18]*SPP[15] - P[15][18]*SPP[21];
nextP[4][18] = P[4][18] + P[15][18]*SF[22] + P[0][18]*SPP[20] + P[1][18]*SPP[12] + P[2][18]*SPP[11];
nextP[5][18] = P[5][18] + P[15][18]*SF[20] - P[0][18]*SPP[7] + P[1][18]*SPP[10] + P[2][18]*SPP[0];
nextP[6][18] = P[6][18] + P[3][18]*dt;
nextP[7][18] = P[7][18] + P[4][18]*dt;
nextP[8][18] = P[8][18] + P[5][18]*dt;
nextP[9][18] = P[9][18];
nextP[10][18] = P[10][18];
nextP[11][18] = P[11][18];
nextP[12][18] = P[12][18];
nextP[13][18] = P[13][18];
nextP[14][18] = P[14][18];
nextP[15][18] = P[15][18];
nextP[16][18] = P[16][18];
nextP[17][18] = P[17][18];
nextP[18][18] = P[18][18];
nextP[0][19] = P[0][19]*SPP[5] - P[1][19]*SPP[4] + P[2][19]*SPP[8] + P[9][19]*SPP[22] + P[12][19]*SPP[18];
nextP[1][19] = P[1][19]*SPP[6] - P[0][19]*SPP[2] - P[2][19]*SPP[9] + P[10][19]*SPP[22] + P[13][19]*SPP[17];
nextP[2][19] = P[0][19]*SPP[14] - P[1][19]*SPP[3] + P[2][19]*SPP[13] + P[11][19]*SPP[22] + P[14][19]*SPP[16];
nextP[3][19] = P[3][19] + P[0][19]*SPP[1] + P[1][19]*SPP[19] + P[2][19]*SPP[15] - P[15][19]*SPP[21];
nextP[4][19] = P[4][19] + P[15][19]*SF[22] + P[0][19]*SPP[20] + P[1][19]*SPP[12] + P[2][19]*SPP[11];
nextP[5][19] = P[5][19] + P[15][19]*SF[20] - P[0][19]*SPP[7] + P[1][19]*SPP[10] + P[2][19]*SPP[0];
nextP[6][19] = P[6][19] + P[3][19]*dt;
nextP[7][19] = P[7][19] + P[4][19]*dt;
nextP[8][19] = P[8][19] + P[5][19]*dt;
nextP[9][19] = P[9][19];
nextP[10][19] = P[10][19];
nextP[11][19] = P[11][19];
nextP[12][19] = P[12][19];
nextP[13][19] = P[13][19];
nextP[14][19] = P[14][19];
nextP[15][19] = P[15][19];
nextP[16][19] = P[16][19];
nextP[17][19] = P[17][19];
nextP[18][19] = P[18][19];
nextP[19][19] = P[19][19];
nextP[0][20] = P[0][20]*SPP[5] - P[1][20]*SPP[4] + P[2][20]*SPP[8] + P[9][20]*SPP[22] + P[12][20]*SPP[18];
nextP[1][20] = P[1][20]*SPP[6] - P[0][20]*SPP[2] - P[2][20]*SPP[9] + P[10][20]*SPP[22] + P[13][20]*SPP[17];
nextP[2][20] = P[0][20]*SPP[14] - P[1][20]*SPP[3] + P[2][20]*SPP[13] + P[11][20]*SPP[22] + P[14][20]*SPP[16];
nextP[3][20] = P[3][20] + P[0][20]*SPP[1] + P[1][20]*SPP[19] + P[2][20]*SPP[15] - P[15][20]*SPP[21];
nextP[4][20] = P[4][20] + P[15][20]*SF[22] + P[0][20]*SPP[20] + P[1][20]*SPP[12] + P[2][20]*SPP[11];
nextP[5][20] = P[5][20] + P[15][20]*SF[20] - P[0][20]*SPP[7] + P[1][20]*SPP[10] + P[2][20]*SPP[0];
nextP[6][20] = P[6][20] + P[3][20]*dt;
nextP[7][20] = P[7][20] + P[4][20]*dt;
nextP[8][20] = P[8][20] + P[5][20]*dt;
nextP[9][20] = P[9][20];
nextP[10][20] = P[10][20];
nextP[11][20] = P[11][20];
nextP[12][20] = P[12][20];
nextP[13][20] = P[13][20];
nextP[14][20] = P[14][20];
nextP[15][20] = P[15][20];
nextP[16][20] = P[16][20];
nextP[17][20] = P[17][20];
nextP[18][20] = P[18][20];
nextP[19][20] = P[19][20];
nextP[20][20] = P[20][20];
nextP[0][21] = P[0][21]*SPP[5] - P[1][21]*SPP[4] + P[2][21]*SPP[8] + P[9][21]*SPP[22] + P[12][21]*SPP[18];
nextP[1][21] = P[1][21]*SPP[6] - P[0][21]*SPP[2] - P[2][21]*SPP[9] + P[10][21]*SPP[22] + P[13][21]*SPP[17];
nextP[2][21] = P[0][21]*SPP[14] - P[1][21]*SPP[3] + P[2][21]*SPP[13] + P[11][21]*SPP[22] + P[14][21]*SPP[16];
nextP[3][21] = P[3][21] + P[0][21]*SPP[1] + P[1][21]*SPP[19] + P[2][21]*SPP[15] - P[15][21]*SPP[21];
nextP[4][21] = P[4][21] + P[15][21]*SF[22] + P[0][21]*SPP[20] + P[1][21]*SPP[12] + P[2][21]*SPP[11];
nextP[5][21] = P[5][21] + P[15][21]*SF[20] - P[0][21]*SPP[7] + P[1][21]*SPP[10] + P[2][21]*SPP[0];
nextP[6][21] = P[6][21] + P[3][21]*dt;
nextP[7][21] = P[7][21] + P[4][21]*dt;
nextP[8][21] = P[8][21] + P[5][21]*dt;
nextP[9][21] = P[9][21];
nextP[10][21] = P[10][21];
nextP[11][21] = P[11][21];
nextP[12][21] = P[12][21];
nextP[13][21] = P[13][21];
nextP[14][21] = P[14][21];
nextP[15][21] = P[15][21];
nextP[16][21] = P[16][21];
nextP[17][21] = P[17][21];
nextP[18][21] = P[18][21];
nextP[19][21] = P[19][21];
nextP[20][21] = P[20][21];
nextP[21][21] = P[21][21];
if (stateIndexLim > 21) {
nextP[0][22] = P[0][22]*SPP[5] - P[1][22]*SPP[4] + P[2][22]*SPP[8] + P[9][22]*SPP[22] + P[12][22]*SPP[18];
nextP[1][22] = P[1][22]*SPP[6] - P[0][22]*SPP[2] - P[2][22]*SPP[9] + P[10][22]*SPP[22] + P[13][22]*SPP[17];
nextP[2][22] = P[0][22]*SPP[14] - P[1][22]*SPP[3] + P[2][22]*SPP[13] + P[11][22]*SPP[22] + P[14][22]*SPP[16];
nextP[3][22] = P[3][22] + P[0][22]*SPP[1] + P[1][22]*SPP[19] + P[2][22]*SPP[15] - P[15][22]*SPP[21];
nextP[4][22] = P[4][22] + P[15][22]*SF[22] + P[0][22]*SPP[20] + P[1][22]*SPP[12] + P[2][22]*SPP[11];
nextP[5][22] = P[5][22] + P[15][22]*SF[20] - P[0][22]*SPP[7] + P[1][22]*SPP[10] + P[2][22]*SPP[0];
nextP[6][22] = P[6][22] + P[3][22]*dt;
nextP[7][22] = P[7][22] + P[4][22]*dt;
nextP[8][22] = P[8][22] + P[5][22]*dt;
nextP[9][22] = P[9][22];
nextP[10][22] = P[10][22];
nextP[11][22] = P[11][22];
nextP[12][22] = P[12][22];
nextP[13][22] = P[13][22];
nextP[14][22] = P[14][22];
nextP[15][22] = P[15][22];
nextP[16][22] = P[16][22];
nextP[17][22] = P[17][22];
nextP[18][22] = P[18][22];
nextP[19][22] = P[19][22];
nextP[20][22] = P[20][22];
nextP[21][22] = P[21][22];
nextP[22][22] = P[22][22];
nextP[0][23] = P[0][23]*SPP[5] - P[1][23]*SPP[4] + P[2][23]*SPP[8] + P[9][23]*SPP[22] + P[12][23]*SPP[18];
nextP[1][23] = P[1][23]*SPP[6] - P[0][23]*SPP[2] - P[2][23]*SPP[9] + P[10][23]*SPP[22] + P[13][23]*SPP[17];
nextP[2][23] = P[0][23]*SPP[14] - P[1][23]*SPP[3] + P[2][23]*SPP[13] + P[11][23]*SPP[22] + P[14][23]*SPP[16];
nextP[3][23] = P[3][23] + P[0][23]*SPP[1] + P[1][23]*SPP[19] + P[2][23]*SPP[15] - P[15][23]*SPP[21];
nextP[4][23] = P[4][23] + P[15][23]*SF[22] + P[0][23]*SPP[20] + P[1][23]*SPP[12] + P[2][23]*SPP[11];
nextP[5][23] = P[5][23] + P[15][23]*SF[20] - P[0][23]*SPP[7] + P[1][23]*SPP[10] + P[2][23]*SPP[0];
nextP[6][23] = P[6][23] + P[3][23]*dt;
nextP[7][23] = P[7][23] + P[4][23]*dt;
nextP[8][23] = P[8][23] + P[5][23]*dt;
nextP[9][23] = P[9][23];
nextP[10][23] = P[10][23];
nextP[11][23] = P[11][23];
nextP[12][23] = P[12][23];
nextP[13][23] = P[13][23];
nextP[14][23] = P[14][23];
nextP[15][23] = P[15][23];
nextP[16][23] = P[16][23];
nextP[17][23] = P[17][23];
nextP[18][23] = P[18][23];
nextP[19][23] = P[19][23];
nextP[20][23] = P[20][23];
nextP[21][23] = P[21][23];
nextP[22][23] = P[22][23];
nextP[23][23] = P[23][23];
}
}
// Copy upper diagonal to lower diagonal taking advantage of symmetry
for (uint8_t colIndex=0; colIndex<=stateIndexLim; colIndex++)
{
for (uint8_t rowIndex=0; rowIndex 1e4f)
{
for (uint8_t i=6; i<=7; i++)
{
for (uint8_t j=0; j<=stateIndexLim; j++)
{
nextP[i][j] = P[i][j];
nextP[j][i] = P[j][i];
}
}
}
// copy covariances to output
CopyCovariances();
// constrain diagonals to prevent ill-conditioning
ConstrainVariances();
hal.util->perf_end(_perf_CovariancePrediction);
} 到目前位置EKF2预测过程的两个公式就讲完了。篇幅有点长，但中心思想就是求这几个方程。