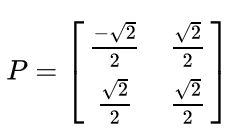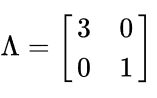机器学习中的数学基础:(1)实际应用中矩阵特征值与特征向量的几何意义
关于特征值、特征向量的讲解有很多的教程,对于这些枯燥的数学基础怎么运用到自己的实际计算机视觉实验中,是一项很重要的任务。算法的底层其实就是数学公式的各种结合与推导,有时间不是我们不能很好的去理解这些算法基础,而是没有一个很好的教程带领我们这些小白去一步步的从底层学习。写博客的目的一方面就是记录自己的总结,另一方面就是用自己的大白话去描述这些专业的术语与思想,方便自己能看懂学习。(以上纯属个人观点)
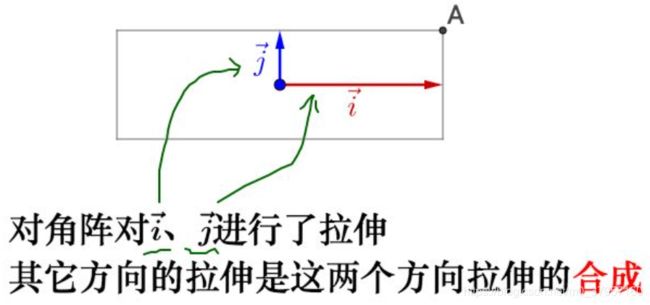
----------矩阵---------
首先,我们把矩阵比作跑步,跑步最重要的就是知道两个要素方向(朝哪个方向跑)和速度(我要跑的多快),而矩阵的特征向量就是跑步的方向,矩阵的特征值就是跑步的速度。(这个比喻只是帮助大家理解怎么由数学概念转换到实际生活运用中)
---------线性变换-------
我们知道,矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。实际上,上述的一段话既讲了矩阵变换特征值及特征向量的几何意义(图形变换)也讲了其物理含义。物理的含义就是运动的图景:特征向量在一个矩阵的作用下作伸缩运动,伸缩的幅度由特征值确定。特征值大于1,所有属于此特征值的特征向量身形暴长;特征值大于0小于1,特征向量身形猛缩;特征值小于0,特征向量缩过了界,反方向到0点那边去了。关于特征值和特征向量,这里请注意两个亮点。这两个亮点一个是线性不变量的含义,二个是振动的谱含义。
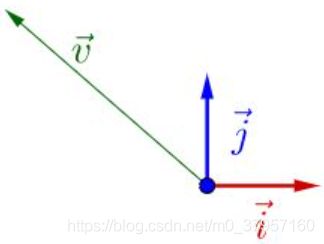
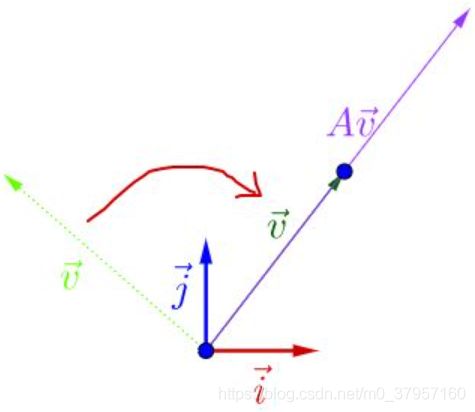
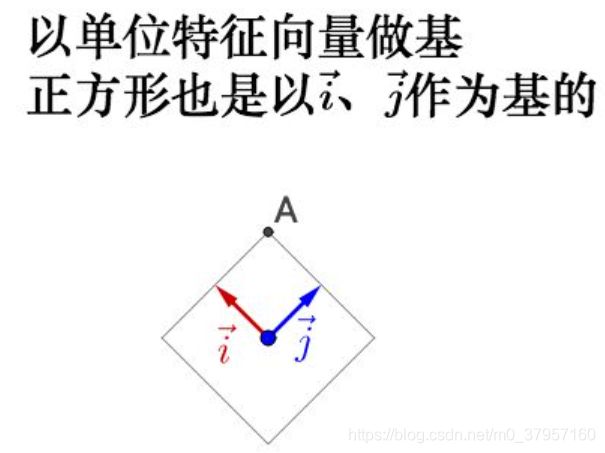
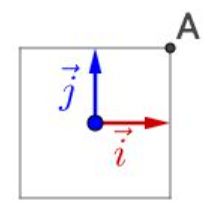
所谓的线性变换(旋转、伸缩)就是向量在不同的基(其实就是单位特征向量组成的坐标系)之间进行变来变去。下图给出了所用的基和原点:
1.在![]() 和
和![]() 基下面有一个
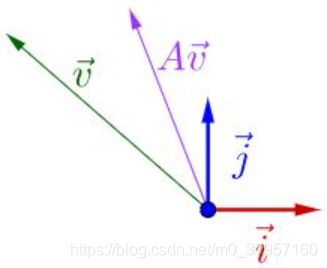
基下面有一个![]() (如左图): 2.将
(如左图): 2.将![]() 左乘一个矩阵A,可得下图(如中图): 3.再将
左乘一个矩阵A,可得下图(如中图): 3.再将![]() 左乘一个矩阵A,可得下图(如右图):
左乘一个矩阵A,可得下图(如右图):
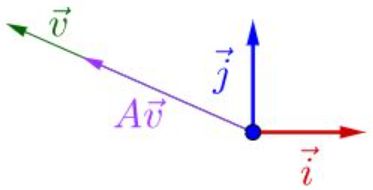
3.下面改变一下![]() 的方向:(如左图) 4.再将
的方向:(如左图) 4.再将![]() 左乘一个矩阵A,可得下图(如右图):
左乘一个矩阵A,可得下图(如右图):
得出结论:
如果存在某个或某些向量在A作用之后,它只是伸长或者缩短,其位置仍停留在其原来张成的直线上,那么称之为A的特征向量,伸长或者缩短的倍数称为对应特征向量的特征值。
1.未改变方向的![]() A
A![]() 在同一条直线上,只是A
在同一条直线上,只是A![]() 的长度要比
的长度要比![]() 短。缩短了
短。缩短了![]() 倍,该
倍,该![]() 是矩阵A的特征值,对应的A
是矩阵A的特征值,对应的A![]() 是矩阵A的特征向量。
是矩阵A的特征向量。
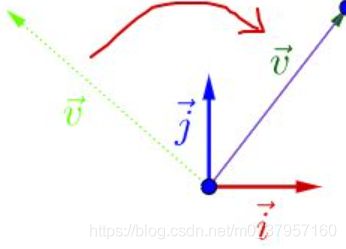
2.经过改变方向后的![]() 和A
和A![]() 在同一条直线上,只是A
在同一条直线上,只是A![]() 的长度要比
的长度要比![]() 长,则
长,则![]() 是矩阵A的特征向量,而A
是矩阵A的特征向量,而A![]() 在长度上是
在长度上是![]() 的
的![]() 倍,该
倍,该![]() 也是矩阵A的特征值。即
也是矩阵A的特征值。即![]() 在矩阵A的作用下,保持方向不变,进行
在矩阵A的作用下,保持方向不变,进行![]() 倍的拉伸。可写作:
倍的拉伸。可写作:
![]() (从上述结果可以看出,矩阵A不止有一个特征值与特征向量,特征向量所在直线上的向量都是特征向量)
(从上述结果可以看出,矩阵A不止有一个特征值与特征向量,特征向量所在直线上的向量都是特征向量)
特征向量所在直线包含了所有的特征向量,这些总的组成了特征空间。
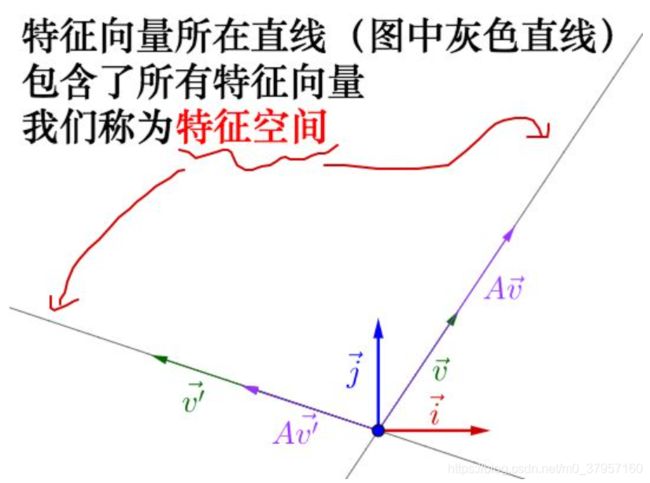 (两个红色箭头就是最大特征值,最小特征值,之间组成了特征空间,改变
(两个红色箭头就是最大特征值,最小特征值,之间组成了特征空间,改变![]() 的位置,以及矩阵A的值,特征空间会随着矩阵的变化而改变,即上述所比喻的跑步,所对应的速度最大的方向就是由最大特征值对应的特征向量表现出来的)
的位置,以及矩阵A的值,特征空间会随着矩阵的变化而改变,即上述所比喻的跑步,所对应的速度最大的方向就是由最大特征值对应的特征向量表现出来的)
特征向量是线性不变量:所谓特征向量概念的亮点之一是不变量,这里叫线性不变量。因为我们常讲,线性变换啊线性变换,不就是把一根线(向量)变成另一根线(向量),线的变化的地方大多是方向和长度一块变。而一种名叫“特征向量”的向量特殊,在矩阵作用下不变方向只变长度。不变方向的特性就被称为线性不变量。(特征向量之所以被称为“特征”,因为它具有不变的特性)
特征值与特征向量性质:
1.只有方阵才有特征值和特征向量
方阵总有特征值,因为总有特征多项式(特征方程),但不是所有方阵都有实数特征解
实方阵一定有实数特征解
2.不同特征值对应的特征向量是线性无关的
3.对于实对称矩阵或埃尔米特矩阵来说,不同特征值对应的特征向量必定正交(相互垂直)
--------举例--------
以对角矩阵为例:
------------相似矩阵---------------
设 A,B 都是 n 阶矩阵,若有可逆矩阵 P ,使![]() AP=B, 则称 B 是 A 的相似矩阵,或说 A 和 B 相似。
AP=B, 则称 B 是 A 的相似矩阵,或说 A 和 B 相似。
运用的几何意义是:同一线性变换在不同基下的表达形式(类似于直角坐标到极坐标系下图像是不会变换的)。(掌握相似矩阵的性质)
----------对角矩阵--------
对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2,…,an) 。对角矩阵可以认为是矩阵中最简单的一种,值得一提的是:对角线上的元素可以为 0 或其他值,对角线上元素相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算,且结果仍为对角阵。
-----矩阵对角化:对n阶矩阵A,如果可以找到可逆矩阵P,使得![]() AP=对角阵,就称为把方阵A对角化。
AP=对角阵,就称为把方阵A对角化。
矩阵对角化的充要条件:n阶矩阵有n个线性无关的特征向量。
推论:若n阶方阵A有n个互不相同的特征值,则A可对角化。而且:1.对角阵的主对角元素为A的特征值。2. 可逆矩阵P由A的n个线性无关的特征向量作列向量构成。
可对角化,是有条件的,这里又用到了特征向量。你只有找到A的n个线性无关的特征向量,才能将A顺利地对角化。
根据特征值与特征向量,用于找矩阵的相似对角阵,非常有意义。
举例:
---------
------特征值分解---------------
首先解释一下为什么这些值叫特征值,这些向量叫特征向量。因为:
1.在相似变换中,这些东西不变,而且其他不变性质可以通过特征值不变来推导;所以特征值是相似的这些矩阵的集合(这一类矩阵)的公共属性,它当然可以作为特征。
2.从几何意义上讲,特征向量描述了矩阵对应的线性变换的主要变换方向。线性变换对向量的作用是伸缩(新的长度)和旋转(新的方向),旋转会消减拉伸的作用,特征向量只有伸缩没有旋转,它就代表了这个线性变换的主要方向;那么特征值就是描述该方向上的变换速度(倍数),所以把特征值排序,从大到小的特征值及其特征向量能近似地描述原矩阵的主变换方向和变换速度。
特征值分解是找最相似的矩阵:
特征值分解是将一个矩阵分解为如下形式: A=Q∑![]() ,
,
其中,Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角矩阵,每一个对角线元素就是一个特征值,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变化方向(从主要的变化到次要的变化排列)。也就是说矩阵A的信息可以由其特征值和特征向量表示。
对于矩阵为高维的情况下,那么这个矩阵就是高维空间下的一个线性变换。可以想象,这个变换也同样有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵(变换)。
总结一下,特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
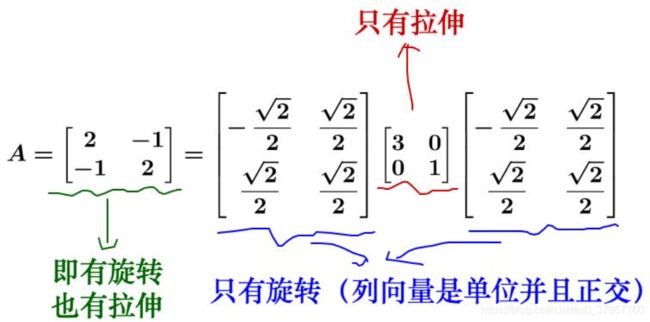
----------具体应用在图像压缩上,比如说,有这么一副512×512的图片(方阵才有特征值),这个图片可以放到一个矩阵里面去,就是把每个像素的颜色值填入到一个512×512512×512的 A 矩阵中。根据之前的矩阵对角化A=p![]()
![]() ,其中
,其中![]() 为对角阵,对角线上是从大到小排列的特征值,我们只保留前面50个的特征值(也就是最大的50个,其实也只占了所有特征值的百分之十),其它的都填0,重新计算矩阵后,利用新得到的矩阵,进行恢复图像,效果仍然与原图像差不多。
为对角阵,对角线上是从大到小排列的特征值,我们只保留前面50个的特征值(也就是最大的50个,其实也只占了所有特征值的百分之十),其它的都填0,重新计算矩阵后,利用新得到的矩阵,进行恢复图像,效果仍然与原图像差不多。
----------------
上述操作发生旋转变成了标准基(如上述右图)
得到如下图:
这两次相乘对应于前边的讲解,第一次乘以P特征向量,(就是对基进行旋转)相当于指明了跑步的方向。第二次乘以![]() 特征值,就是指明了跑步的速度的大小。
特征值,就是指明了跑步的速度的大小。
因此如果特征向量正交,这样就能保证变换的最大方向在基方向,如果特征向量不正交就不能保证变换在最大方向上。因此,在实际应用中就要去找正交基,但是特征向量很有可能不是正交的,故需要奇异值分解(SVD)。
3.在上述基础上再次的左乘![]() ,就会把基变换回去。如下图:
,就会把基变换回去。如下图:
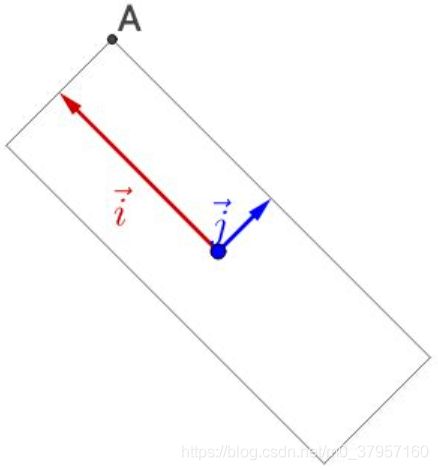 (在此整个过程中只是把整个图像坐标系给旋转、拉伸了而已。图像并没有变化)
(在此整个过程中只是把整个图像坐标系给旋转、拉伸了而已。图像并没有变化)
//Python求特征值与特征向量
>>> import numpy as np
>>> a=np.array([[2,-1],[-1,2]])
>>> a
array([[ 2, -1],
[-1, 2]])
>>> e,q=np.linalg.eig(a)
>>> e # 特征值
array([ 3., 1.])
>>> q # 特征向量作为列向量
array([[ 0.70710678, 0.70710678],
[-0.70710678, 0.70710678]])
>>>
>>> a=np.array([[1,2,3],[3,2,5],[1,10,8]])
>>> e,q=np.linalg.eig(a)
>>> e
array([ 13.50864036, -0.42667365, -2.0819667 ])
>>> q
array([[-0.27543318, -0.6534998 , -0.23748816],
[-0.44255955, -0.44847532, -0.67779488],
[-0.85339183, 0.60976053, 0.69584012]])
>>>
>>> E=np.diag(e) # 对角阵
>>> E
array([[ 13.50864036, 0. , 0. ],
[ 0. , -0.42667365, 0. ],
[ 0. , 0. , -2.0819667 ]])
图片截取来自知乎。