Wasserstein GAN

Wasserstein GAN

1. 简介

本文所关注的问题是无监督学习问题。最主要的是，学习概率分布意味着什么？经典的答案是学习概率密度。这通常是通过定义一个参数密度族$(P_{\theta }{)}_{\theta \in {\mathbb{R}}^d}$，并在我们的数据上找到一个最大的可能性：如果我们有真实的数据示例$\{x^i{\}}_{i-1}^m$，我们就会解决这个问题:
$$\underset{\theta \in {\mathbb{R}}^d}{\max }\frac{1}{m}\sum _{i=1}^{m}log{P}_{\theta }(x^i)$$
如果真实数据分布 ${\mathbb{P}}_r$ 提供了密度，且 ${\mathbb{P}}_{\theta }$ 是参数化密度 $P_{\theta }$ 的分布，则渐近地，这等于最小化KL散度 $KL({\mathbb{P}}_r||{\mathbb{P}}_{\theta })$。

为了使这个有意义，我们需要模型密度 $P_{\theta }$ 存在。在我们处理相当常见的由低维流形支持的分布的情况下，情况就不是这样了。这样，模型流形和真实分布的支撑就不可能有一个不可忽略的交集，这意味着 $KL$ 距离是无定义的(或者说是无限的)。

典型的补救措施是在模型分布中添加噪声项。这就是为什么在经典机器学习文献中描述的几乎所有生成模型都包含噪声成分。在最简单的情况下，我们假设一个相对具有较高的带宽的高斯噪声，以涵盖所有的例子。众所周知，例如，在图像生成模型的情况下，这种噪声降低了样本的质量，使它们变得模糊。例如，我们在文献中可以看到，当最大似然时，模型中添加的噪声的最佳标准偏差约为生成图像中每个像素的 $0.1$ 倍，而且前提是像素已经归一化到$[0,1]$ 范围内了。这是一个非常高的噪音量，以至于当论文报告他们的模型的样本时，他们不会在他们报告的最大似然数中加入噪声项。换句话说，附加的噪声项对于这个问题显然是不正确的，但是为了使最大似然法工作是必需的。

相比于估计一个可能不存在的密度 ${\mathbb{P}}_r$，我们可以定义一个服从固定分布 $p(z)$ 的随机变量 $Z$，并且通过一个参数化方法$g_{\theta }:\mathcal{Z}\to \mathcal{X}$ （通常是一种神经网络）来指导生成样本服从一个特定的分布 ${\mathbb{P}}_{\theta }$，通过改变$\theta$，我们可以改变这种分布并使其接近真实数据分布 ${\mathbb{P}}_r$。 这在两个方面很有用。 首先，与密度不同，这种方法可以表示限制在低维流形的分布。其次，更容易生成样本的能力通常比密度已知的数值更加有用（例如，在超分辨率图像或语义分割中，考虑给定输入图像的输出图像的条件分布）。通常，在给定任意高维密度的情况下生成样本的计算是非常困难的。

变分自动编码器（VAE）和生成性对抗网络（GAN）是这种方法的众所周知的例子。 由于VAE关注的是示例的近似可能性，因此它们共享标准模型的局限性，需要额外操作噪声项。GAN在目标函数的定义中提供了更多的灵活性，包括Jensen-Shannon和f-divergence以及一些奇异的组合，但是另一方面， GAN训练以脆弱和不稳定而着称。

在本文中，我们将注意力集中在测量模型分布和实际分布关系的各种方法上，或等效地，用于定义距离或散度 $\rho ({\mathbb{P}}_{\theta },{\mathbb{P}}_r)$ 的各种方法。 这些距离之间最基本的差异是它们对概率分布序列收敛的影响。当且仅当存在分布 ${\mathbb{P}}_{\infty }$ 使得 $\rho ({\mathbb{P}}_t,{\mathbb{P}}_{\infty })$ 倾向于零，分布序列 $({\mathbb{P}}_t{)}_{t\in \mathbb{N}}$ 才会收敛，这取决于距离$\rho$ 的确定程度。 非正式地，当一个分布序列较容易收敛时，则距离是$\rho$ 一个较弱的拓扑结构。第二部分阐明了在这方面的概率距离有多么流行。

为了优化参数 $\theta$，我们当然希望以使得映射 $\theta \mapsto {\mathbb{P}}_{\theta }$ 连续的方式定义我们的模式分布${\mathbb{P}}_{\theta }$。 连续性意味着当一系列参数${\theta }_t$收敛到 $\theta$ 时，分布 ${\mathbb{P}}_{{\theta }_t}$ 收敛到 ${\mathbb{P}}_t$。 但是，必须记住，分布收敛的概念取决于我们计算分布之间距离的方式。 这个距离越弱，就越容易定义从 $\theta$ 空间到 ${\mathbb{P}}_{\theta }$ 空间的连续映射，因为它更易于分布的收敛。 我们关心映射 $\theta \mapsto {\mathbb{P}}_{\theta }$ 是连续的主要原因是：如果是 $\rho$ 我们两个分布之间距离的概念，我们希望有一个连续的损失函数 $\theta \mapsto \rho ({\mathbb{P}}_{\theta },{\mathbb{P}}_r)$，这相当于当使用距离分布 $\rho$ 时，映射$\theta \mapsto {\mathbb{P}}_{\theta }$是连续的。

本文的贡献是：

• 在第2节中，我们提供了一个全面的理论分析，分析了EarthMover（EM）距离与学习分布环境中使用的流行概率距离和差异的比较。
• 在第3节中，我们定义了一种称为Wasserstein-GAN的GAN形式，它最小化了EM距离的合理有效近似，并且从理论上表明相应的优化问题是合理的。
• 在第4节中，我们凭经验证明WGAN可以解决GAN的主要训练问题。特别是，训练WGAN不需要在判别器和生成器的训练中保持谨慎的平衡，也不需要仔细设计网络架构。 GAN中典型的模式化现象也大大减少.WGAN最引人注目的实际好处之一是能够通过训练判别器来优化连续估计EM距离。绘制这些学习曲线不仅对调试和超参数搜索有用，而且与观察到的样本质量非常相关。

2. 不同的距离

现在介绍我们的符号。 令$\mathcal{X}$为一个紧凑的矩阵集（例如图像的空间$[0,1]d$），让$\Sigma$表示$\mathcal{X}$的所有Borel子集的集合。 使$Prob(X)$表示在$\mathcal{X}$上定义的概率测量的空间。 我们现在可以定义两个分布之 ${\mathbb{P}}_r,{\mathbb{P}}_g\in Prob(\mathcal{X})$ 间的基本距离和差异。

（Borel集：$R^n$ 中一切开集构成的开集族，生成的$\sigma$代数称为$R^n$的borel $\sigma$代数，它其中的元素称为 borel集。borel集由开集的有限次的并，交，差构成。borel对于测度理论非常重要，因为每个定义在开集上或者闭集的测度，都需要在哪个空间的所有的borel集上定义。）

• 总变差(TV)距离：

$$\delta ({\mathbb{P}}_r,{\mathbb{P}}_g)=\underset{A\in \sum }{\sup }|{\mathbb{P}}_r(A)-{\mathbb{P}}_g(A)|$$

• KL散度：

$$KL({\mathbb{P}}_r||{\mathbb{P}}_g)=\int log(\frac{P_r(x)}{P_g(x)})P_r(x)d\mu (x)$$

其中假设${\mathbb{P}}_r$和${\mathbb{P}}_g$都是绝对连续的，因此相对于相同的测量$\mu$ ，在$\mathcal{X}$上定义密度，并且当存在$P_g（x）=0$和$P_r（x）>0$的点时，众所周知KL散度就会变得的不对称并且可能是无穷的。

• JS散度：

$$JS(P_r,P_g)=KL(P_r,\frac{P_r+P_g}{2})+KL(P_g,\frac{P_r+P_g}{2})$$

• EM距离或Wasserstein距离:

$$W(P_r,P_g)=\underset{y\in \prod (P_r,P_g)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]\text{\hspace{1em}(1)}$$

其中$\prod (P_r,P_g)$表示所有联合分布$\gamma (x,y)$的集合，其边缘分别为$P_r,P_g$。直观的，$\gamma (x,y)$表示从x 到 y 必须输入多少能量，以讲分布$P_r$转换为分布$P_g$。然后，EM距离是最佳运输计划的成本。

以下示例说明了概率分布的简单序列如何在EM距离下收敛，但在上面定义的其他距离和散度下不收敛。

例一：设$Z\sim U[0,1]$在单位区间内独立分布，使${\mathbb{P}}_0$作为$(0,Z)\in {\mathbb{R}}^2$的分布（0在x轴上，Z在y轴上），${\mathbb{P}}_0$ 在穿过原点的垂线上均匀分布，现在令$g_{\theta }(z)=(\theta ,z)$ ($\theta$为一个单独的实参）。在这个例子中很容易看到：

• $W({\mathbb{P}}_0,{\mathbb{P}}_{\theta })=|\theta |$

• $JS({\mathbb{P}}_0,{\mathbb{P}}_{\theta })=\{\begin{array}{ll}-x& \text{if}\theta ̸=0,\\ 0& \text{if}\theta =0,\end{array}$

• $KL({\mathbb{P}}_{\theta }\Vert {\mathbb{P}}_0)=KL({\mathbb{P}}_0\Vert {\mathbb{P}}_{\theta })=\{\begin{array}{ll}+\infty & \text{if}\theta ̸=0,\\ 0& \text{if}\theta =0,\end{array}$

• $and\delta ({\mathbb{P}}_0,{\mathbb{P}}_{\theta })=\{\begin{array}{ll}1& \text{if}\theta ̸=0,\\ 0& \text{if}\theta =0.\end{array}$

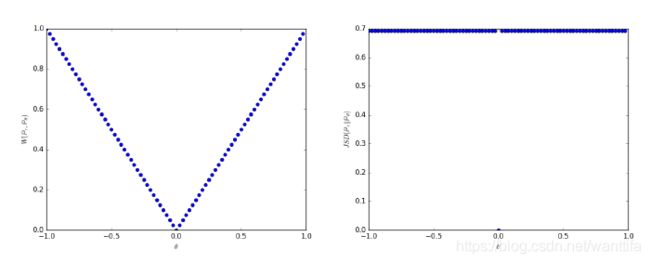
当 ${\theta }_t\to 0$ 时，序列$({\mathbb{P}}_{{\theta }_t}{)}_{t\in \mathbb{N}}$ 在EM距离下收敛于${\mathbb{P}}_0$ ，但是在JS，KL，反向KL或TV距离下都没有收敛。图1说明了EM和JS距离的情况：

Figure 1: These plots show $\rho ({\mathbb{P}}_{\theta };{\mathbb{P}}_0)$ as a function of $\theta$ when $\rho$ is the EM distance (left plot) or the JS divergence (right plot). The EM plot is continuous and provides a usable gradient everywhere. The JS plot is not continuous and does not provide a usable gradient.

例一给出了一个案例，我们可以通过在EM距离上的梯度下降来学习低维流形的概率分布。这不能用其他距离和散度来完成，因为产生的损失函数甚至会不连续。虽然这个简单示例的特征分布的支撑集不相交（就是${\mathbb{P}}_0,{\mathbb{P}}_{\theta }$ 不想交)，但是当支撑集${\mathbb{P}}_0,{\mathbb{P}}_{\theta }$具有测度为零的非空交集时，结论同样成立。 当两个低维流形在一般位置相交时，恰好就是这种情况.

由于Wasserstein距离远远弱于JS距离，我们现在可以温和的假设一下：$W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$是否是关于$\theta$的连续损失函数。这个假设是正确的，正如我们现在陈述和证明的那样。

定理1： 设${\mathbb{P}}_r$是$\mathcal{X}$的固定分布，设Z是另一个空间$\mathcal{Z}$上的随机变量（例如高斯），设$\mathcal{Z}\times {\mathbb{R}}^d\to \mathcal{X}$ 是一个函数，用$\theta$表示$g_{\theta }(z)$的第一个坐标且$\theta$为第二个，令${\mathbb{P}}_{\theta }$表示$g_{\theta }(Z)$的分布。则：

1. 如果$g$在$\theta$上是连续的，那么$W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$也是。
2. 如果$g$是局部Lipschitz并且满足规律性假设1，那么$W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$处处连续切可微。
3. 对于$JS({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$和所有KL，陈述1-2都是错误的。

以下推论告诉我们，通过最小化EM距离来使神经网络学习至少在理论上是有意义的。

**推论1.**假设$g_{\theta }$是由$\theta$参数化的任一前馈神经网络，并且$p(z)$优先于$z$，使得${\mathbb{E}}_{z\sim p(z)}[\Vert z\Vert ]<\infty$ (例如高斯，均匀等).

然后假设1被满足，因此$W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$在任何地方都是连续的并且几乎在任何地方都是可微的。

所有这些都表明，对于我们的问题而言，EM至少相比于JS是一个更明智的损失函数。 下面的定理描述了由这些距离和偏差引起的拓扑的相对强度，其中KL最强，其次是JS和TV，而EM最弱。

定理2： 设$\mathbb{P}$是密集空间$\mathcal{X}$的一个分布，并且$({\mathbb{P}}_n{)}_{n\in \mathbb{N}}$是$\mathcal{X}$上的序列分布。然后，将所有极限都视为$n\to \infty$，

1. 以下陈述是等价的
   • $\delta ({\mathbb{P}}_n,\mathbb{P})\to 0$总变差距离
   • $JS({\mathbb{P}}_n,\mathbb{P})$ JS散度
2. 以下陈述是等价的
   • $W({\mathbb{P}}_n,\mathbb{P})\to 0$
   • ${\mathbb{P}}_n\stackrel{\mathcal{D}}{⟶}\mathbb{P}$ 这里$\stackrel{\mathcal{D}}{⟶}$表示随机变量分布的收敛
3. $KL({\mathbb{P}}_n\Vert \mathbb{P})\to 0orKL(\mathbb{P}\Vert {\mathbb{P}}_n)$暗示等式（1）中的陈述。
4. 等式（1）中的陈述暗示等式（2）中的陈述

这突出了这样一个事实：当学习由低维流形支持的分布时，KL，JS和TV距离不是合理的代价函数。不过，EM距离在该体系中是合理的。 这显然引导我们进入下一部分，我们将介绍优化EM distance的实际近似。

3.Wasserstein GAN

同样，定理2指出$W(P_r,P_{\theta })$在优化$JS(P_r,P_{\theta })$时可能具有更好的性质。 然而，等式（1）中的下限是非常难以处理的。另一方面，Kantorovich-Rubinstein二元性告诉我们：
$$W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })=\underset{\Vert f{\Vert }_L\le 1}{\sup }{\mathbb{E}}_{x\sim {\mathbb{P}}_{\theta }}[f(x)]-{\mathbb{E}}_{x\sim {\mathbb{P}}_r}[f(x)]\text{\hspace{1em}(2)}$$
上确界在所有1-Lipschitz函数$f:\mathcal{X}\to \mathbb{R}$之上。 注意，如果我们替换$\Vert f{\Vert }_L\le 1for\Vert f{\Vert }_L\le K$（考虑某些常数K的K-Lipschitz连续），那么我们最终得到$K\cdot W({\mathbb{P}}_r,{\mathbb{P}}_g)$。 因此，如果我们有一个参数族化的函数$\{f_w{\}}_{w\in W}$，对于某些K来说都是K-Lipschitz，那么我们可以考虑解决如下问题：
$$\underset{w\in W}{\max }{\mathbb{E}}_{x\sim {\mathbb{P}}_r}[f_w(x)]-{\mathbb{E}}_{z\sim p(z)}[f_w(g_{\theta }(z))]\text{\hspace{1em}(3)}$$
并且如果（2）中的上确界达到某个$w\in W$（在证明估计量的一致性时所假设的非常强的假设），则该过程将产生一个直到常数相乘的计算$W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$。 此外，我们可以考虑通过估计${\mathbb{E}}_{z\sim p(z)}[{\nabla }_{\theta }{f}_w(g_{\theta }(z))]$反推等式（2）来区分$W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$（再次，直到常数）。 虽然这都是直觉（假设），但我们现在证明这个过程是在最优性假设下的.

定理3. 设${\mathbb{P}}_r$是任意分布。 设${\mathbb{P}}_{\theta }$为$g_{\theta }(Z)$的分布，Z为随机变量，密度为p， 为满足假设1的函数。然后，对问题有一个解$f:\mathcal{X}\to \mathbb{R}$，问题:
$$\underset{\Vert f{\Vert }_L\le 1}{\max }{\mathbb{E}}_{x\sim {\mathbb{P}}_r}[f(x)]-{\mathbb{E}}_{x\sim {\mathbb{P}}_{\theta }}[f(x)]$$
并且当两个部分都明确定义时我们得到：
$${\nabla }_{\theta }W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })=-{\mathbb{E}}_{z\sim p(z)}[{\nabla }_{\theta }f(g_{\theta }(z))]$$
现在出现的问题是找到解决等式（2）中最大化问题的函数 $f$。 为了粗略地估计这一点，我们可以做的事情是训练一个带有权重$w$的参数化神经网络，在一个密集的空间$W$中，然后通过 ${\mathbb{E}}_{z\sim p(z)}[{\nabla }_{\theta }{f}_w(g_{\theta }(z))]$ 进行反向传播，就像我们对典型的Gan一样。 注意，$W$是密集的这一事实意味着所有函数$f_w$对于某些$K$而言将会是K-Lipschitz连续的，其取决于$W$（全部的$w$）而不是单独的$w$，因此近似于等式（2）直到不相关的缩放因子和’critic’的函数$f_w$。 为了让参数$w$位于一个密集的空间中，我们可以做的一件事就是在每次梯度更新后将权重固定到一个范围（比如$W=[-0.01,0.01{]}^l$）。 Wasserstein生成性对抗网络（WGAN）过程在算法1中描述。

权重限制（Weight clipping）是强制执行Lipschitz约束的一种明显糟糕的方法。 如果限制参数很大，那么任何权重都可能需要很长时间才能达到他们的极限，从而使critic更难以进行优化。 如果限制很小，当层数多或者不使用批量归一化时（例如在RNN中），这就很容易导致梯度消失。 我们尝试了简单的变体（例如将权重投射到球体上），但由于其简单和良好的性能，我们还是坚持使用权重限制。但是，我们还在对神经网络设置中强制执行Lipschitz约束这一操作进行进一步调查 ，我们积极鼓励感兴趣的研究人员改进这种方法。

事实上EM距离是连续且可微分的a.e.（几乎处处收敛）。意味着我们可以训练critic直到最优。这个论点很简单，我们越训练critic，我们得到的Wasserstein的梯度越可靠，这实际上是因为Wasserstein几乎无处不在的这个事实。对于JS来说，随着critic越来越好越来越可靠，但是真实的梯度会变为0，因为JS局部饱和，我们会得到消失的梯度，如本文图1和定理2.4（前篇的）所示。在图2中，我们展示了这一概念的证明，其中我们训练GAN的discriminator和WGAN的critic直到最优。discriminator学得非常快，可以区分假样本和真实样本，并且正如预期的那样，没有提供可靠的梯度信息。然而，critic不能饱和，并且收敛到线性函数，在任何地方都给出了非常干净的渐变。事实上我们约束权重，限制了函数在空间的不同部分中的最多线性的可能增长，迫使最优critic具有这种行为。

也许更重要的是，我们可以训练critic直到最优，这不会使我们模式崩塌。 因为模式崩塌来自这样一个事实，即最优generator是固定discriminator的，他是由 discriminator分配最高值的点上的增量之和。，如[4]所示并在[11]中突出显示。

在下一节中，我们将展示新算法的实际优势，并对其行为与传统GAN的行为进行深入比较。

Figure 2: Optimal discriminator and critic when learning to differentiate two Gaussians.
As we can see, the discriminator of a minimax GAN saturates and results in vanishing
gradients. Our WGAN critic provides very clean gradients on all parts of the space.

4.实验结果

我们使用Wasserstein-GAN算法进行图像生成实验，并显示它比标准GAN的公式的优点。

我们说明了有两个主要好处：

• 一种与生成器收敛性、质量相关的有意义的损失度量

• 提高优化过程的稳定性

4.1实验程序

我们进行图像生成实验。要学习的目标分布是LSUN-Bedrooms数据集，室内卧室的自然图像集合。我们的基线比较是DCGAN，一个使用$-logD$技巧的用标准GAN程序训练的卷积结构的GAN。 生成的样本是尺寸为64x64像素的3通道图像。 我们使用算法1中指定的超参数进行所有实验。

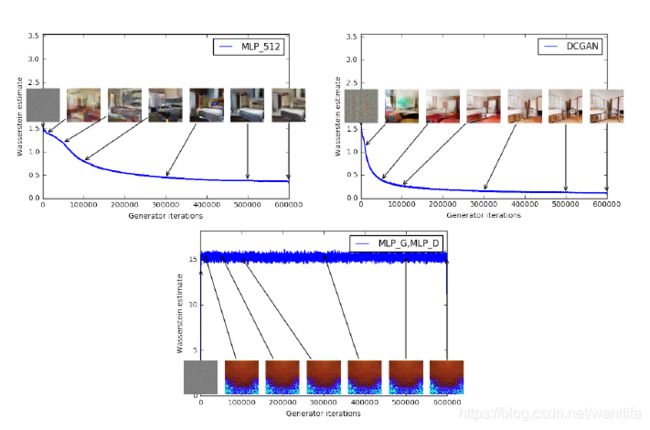
Figure 3: Training curves and samples at different stages of training. We can see a clear correlation between lower error and better sample quality. Upper left: the generator is an MLP with 4 hidden layers and 512 units at each layer. The loss decreases consistently as training progresses and sample quality increases. Upper right: the generator is a standard DCGAN. The loss decreases quickly and sample quality increases as well. In both upper plots the critic is a DCGAN without the sigmoid so losses can be subjected to comparison. Lower half: both the generator and the discriminator are MLPs with substantially high learning rates (so training failed). Loss is constant and samples are constant as well. The training curves were passed through a median filter for visualization purposes.

图三：上在不同的训练阶段的训练曲线和样本。我们可以看到较低的误差和较好的样品质量之间的明确相关性。左上角：生成器是一个带有4个隐藏层的MLP，每层有512个单元。 损失逐渐减少，样本质量增加。 右上：生成器是标准DCGAN。损失迅速减少，样品质量也随之增加。 在两个上图中，critic都是没有sigmoid激活函数DCGAN，因此可以对损失进行比较。下半部分：生成器和discriminator都是具有相当高学习率的MLP（因此训练失败）。 损失是恒定的，样本也是恒定的。 为了可视化目的，我们将训练曲线通过了中值滤波器.

4.2有意义的损失度量

因为WGAN算法试图在每次生成器更新（算法1中的第10行）之前相对较好地训练critic（算法1中的第2-8行），所以此时的损失函数是EM距离的一个估计，直到与我们约束f的Lipschitz常数的方式相关的常数因子。

我们的第一个实验说明了这种估计如何与生成的样本的质量很好地相关。除了DCGAN卷积架构，我们还进行了实验，我们用512个隐藏单元的4层ReLU-MLP替换生成器，或者同时替换生成器和critic。

图3描绘了对于所有三种架构WGAN估计的演变。该图清楚地表明这些曲线与生成样本的视觉质量很好地相关。

据我们所知，这是GAN文献中第一次显示出这样的属性，其中GAN的loss显示了收敛性。在对抗性网络中进行研究时，此属性非常有用，因为不需要盯着生成样本来确定模型的好坏。

Figure 4: JS estimates for an MLP generator (upper left) and a DCGAN generator (upper right) trained with the standard GAN procedure. Both had a DCGAN discriminator. Both curves have increasing error. Samples get better for the DCGAN but the JS estimate increases or stays constant, pointing towards no signi cant correlation between sample quality and loss. Bottom: MLP with both generator and discriminator. The curve goes up and down regardless of sample quality. All training curves were passed through the same
median lter as in Figure 3.

图四：左上的是MLP生成器的JS估计，右上的是一个DCGAN生成器。 他们都是使用标准GAN程序训练的，两者都有一个DCGAN卷积鉴别器，可以看到他们的error是逐渐上升的。 DCGAN的样本越变越好，但JS估计随着迭代的增加而增加或后期基本保持不变，这表明样本质量和损失之间没有显着的相关性。 底部：MLP同时具有生成器器和鉴别器。 无论样品质量如何，曲线都会上下移动。 上面所有训练曲线都通过了与图3中相同的中值滤波器。

但是，我们并未声称这是一种定量评估生成模型的新方法。依赖于critic体系结构的恒定比例的因子意味着很难将模型与不同的critic进行比较。 更重要的是，在实践中，critic没有无限的能力，这使我们很难知道我们的估计到底与EM距离有多接近。 话虽如此，我们已经成功地使用损失度量来反复验证我们的实验，并且没有失败，我们认为这是对GAN训练的巨大改进，以前是没有这样的操作的。

相比之下，图4描绘了GAN训练中以JS距离为根本的GAN估计的变化（也就是JS估计的变化）。 更确切地说，在GAN训练期间，训练鉴别器最大化
$$L(D,g_{\theta })={\mathbb{E}}_{x\sim {\mathbb{P}}_r}[logD(x)]+{\mathbb{E}}_{x\sim {\mathbb{P}}_{\theta }}[log(1-D(x))]$$
他是$2JS({\mathbb{P}}_r,{\mathbb{P}}_{\theta })-2log2$ 的下界。在图中，我们还画出了数量$\frac{1}{2}L(D,g_{\theta })+log2$ ，他是JS距离的下界。

该数量明显与样品质量相关。 另请注意，JS估计通常保持不变或上升而不是下降。 实际上他仍然非常接近$log2\approx 0.69$，这是JS距离取到的最高值。 换句话说，JS距离饱和，鉴别器具有零损失，并且生成的样本在某些情况下是有意义的（DCGAN生成器，右上图），并且在其他情况下折叠成单个无意义的图像[4]。 最后一种现象已在[1]中进行了理论解释，并在[11]中得到了强调。

使用$-log$技巧时，鉴别器loss和生成器loss不同。 附录E中的图8报告了GAN训练的相同图，但使用了loss器损失而不是鉴别器loss。 这不会改变结论。

最后，作为否定结果，我们报告说，当一个人对critic使用基于动量的优化器（例如Adam [8]（对于$\beta 1>0$）或当使用高学习率时，WGAN训练变得不稳定。 由于critic的loss是非常稳定的，所以基于动量的方法似乎表现得更差。 我们将动量确定为潜在原因，因为随着loss的爆发和样本变得更糟，Adam的步和梯度之间的余弦通常变为负值。 这个余弦是负数的唯一的地方就是在这些不稳定的情况下。 因此，我们改用RMSProp [21]，即使在非常不稳定的问题上他也能有良好的表现 [13]。

4.3改善稳定性

WGAN的一个好处是它允许我们训练critic直到最优。当critic接受训练完成时，它只会给我们提供生成器的loss，就像任何其他训练的神经网络一样。 这告诉我们，我们不再需要正确平衡生成器和鉴别器的训练量。critic越好，我们用来训练生成器的梯度越高。

我们还观察到，当选择一个不同的生成器的架构时，WGAN比GAN更强大。 我们通过在三种发生器架构上运行实验来说明这一点：（1）卷积DCGAN生成器，（2）卷积DCGAN生成器，无需批量归一化和具有相同数量的滤波器，以及（3）有512个隐藏单位的4层ReLU -MLP。 已知最后两个与GAN表现很差。 我们为WGAN的critic或GAN的discriminator保留了卷积DCGAN的架构。

图5,6和7展示出了使用WGAN和GAN算法为这三种体系结构生成的样本。我们建议读者引用附录F以获取生成样本的完整表。样品没有被挑选出来.

在没有试验的情况下，我们看到了WGAN算法模式崩塌的证据。

图五：两个算法都是用一个DCGAN的generator训练的，左图是WGAN算法，右图是标准GAN方程，两个算法都生产出了高质量的样本。

图6：算法生成器的训练没有使用批量标准化的算法，每一层的过滤器也没有使用的常数数量（为了不让每次都重复它们，如[18]中所述）。除了去除了批量标准化之外，参数的数量也减少了一些，减少了超过一个数量级。 左：WGAN算法。 右：标准GAN方程。 我们可以看到标准GAN未能正常学习，而WGAN仍然可以生产样本。

图7：（标准GAN算法）使用MLP生成器训练的算法，该生成器有4层，共512个具有ReLU非线性激活函数的单元。参数的数量类似于DCGAN的数量，但它缺乏用于图像生成的强烈的感应偏差。左：WGAN算法。右：标准GAN算法。 WGAN算法仍然能够生成质量低于DCGAN的样本，并且质量高于标准GAN的MLP。请注意GAN MLP中模式崩塌的程度。

5.相关工作

这里有许多关于所谓的积分概率指标（IPM）的著作。 给定F一组是从X到R的函数，我们可以定义：
$$d_{\mathcal{F}}({\mathbb{P}}_r,{\mathbb{P}}_{\theta })=\underset{f\in \mathcal{F}}{\sup }[f(x)]-{\mathbb{E}}_{x\sim {\mathbb{P}}_{\theta }}[f(x)]\text{\hspace{1em}(4)}$$
作为与函数类F相关联的积分概率度量。很容易证实，如果对于每个$f\in F$我们都有$-f\in F$，那么$d_{\mathcal{F}}$是非负的，满足三角不等式，并且是对称的。 因此，$d_{\mathcal{F}}$是Prob（X）的伪测量。

​ 虽然IPM似乎可以分享类似的公式，但我们将看到不同类别的方程可以与完全不同的指标相提并论。

• 通过Kantorovich-Rubinstein二元性[22]，我们知道当$\mathcal{F}$是1-Lipschitz函数的集合时$W({\mathbb{P}}_r,{\mathbb{P}}_{\theta })=d_{\mathcal{F}}({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$ 。 此外，如果$\mathcal{F}$是K-Lipschitz函数的集合，我们得到$K\cdot W(\mathbb P_r,\mathbb P_\theta)=d_\mathcal F(\mathbb P_r,\mathbb P_\theta) $。

• 当F是所有界定在-1和1之间可测量函数的集合时，（或-1和1之间的所有连续函数），我们检索$d_{\mathcal{F}}({\mathbb{P}}_r,{\mathbb{P}}_{\theta })=\delta ({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$ 的总变差距离[15]。 这已然告诉我们，从1-Lipschitz到1-Bounded函数大大改变了空间的拓扑结构，并且$d_\mathcal F(\mathbb P_r,\mathbb P_\theta) $的规律作为损失函数（如定理1和2所示）。

• Energy-based GAN（EBGAN）[25]可以被认为是总变差距离的生成方法。这种连接在附录D中有说明和证明。连接的核心是鉴别器将起到最大化方程（4）的作用，而它的唯一限制是对于某些常数在0和m之间。 这将使得相同的行为被限制在介于-1和1之间，直到与优化无关的恒定的缩放因子。 因此，当鉴别器接近最优时，生成器的成本将使总变差距离$\delta ({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$ 近似。

  由于总变差距离显示出与JS相同的规律性，可以看出EBGAN将遭到与经典GAN相同的问题，即不能将鉴别器训练到最优性并且因此将其自身限制在非常不完美的梯度。

• 最大平均差异（MMD）[5]是积分概率度量的特殊情况，当某些Reproducing Kernel Hilbert Space（RKHS）的 $\mathcal{F}=\{f\in \mathcal{H}:\Vert f{\Vert }_{\infty }\le 1\}$ 与给定的内核$k:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$相关时 。正如[5]所述，我们知道MMD是一个合适的度量标准，而且当内核是通用的时候，它不仅仅是伪计量。在对于$\mathcal{X}$ 上的归一化Lebesgue度量m的方程$\mathcal{H}=L^2(\mathcal{X},m)$ 的特定情况下，我们知道F中包含$\{f\in C_b(\mathcal{X})\Vert f{\Vert }_{\infty }\le 1\}$ ，因此$d_{\mathcal{F}}({\mathbb{P}}_r,{\mathbb{P}}_{\theta })\le \delta ({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$ 作为损失函数的MMD距离的规律性至少与总变差之一一样差。然而，这是一个非常极端的情况，因为我们需要一个非常强大的内核来逼近整个$L^2$ 。然而，即使是Gaussian内核也能够检测出微小的噪声模型，如[20]所证明的那样。这表明，特别是对于低带宽内核，距离可能接近饱和状态，类似于总变差或JS。这显然不一定是每个内核的情况，并且寻找出如何以及哪些不同的MMD更接近Wasserstein或总变差距离是一个有趣的研究课题。

  MMD的一个重要方面是通过内核技巧，不需要为RKHS的球提供单独的网络来最大化方程（4）。但是，这样做的缺点是评估MMD距离的计算成本会以二次方的增长速度而增加。 用于估计（4）中预期的样本量。 最后一点使得MMD具有有限的可扩展性，并且有时不适用于许多现实生活中的应用程序。 MMD [5]有线性计算成本的估计值，在很多情况下MMD非常有用，但它们的样本复杂度也较差。

• Generative Moment Matching Networks (GMMNs) [10,2]是MMD的一个对应模型。通过对核化公式序列（4）进行反向推导，他们直接优化了 $d_{MMD}({\mathbb{P}}_r,{\mathbb{P}}_{\theta })$ （当前一项中的是F时，则是IPM）。如上所述，这具有不需要单独的网络来近似最大化等式（4）的优点。但是，GMMN的适用性有限。对于不成功的部分解释是二次成本作为样本数量和低带宽内核中消失的梯度的函数。此外，实际使用的某些内核可能不适合在高维样本空间（例如自然图像）中捕获非常复杂的距离。 [19]表明，对于典型的高斯MMD测试来说，可靠性（因为它的统计测试接近1的能力），我们需要使样本的数量随着维数的数量线性增长。由于MMD计算成本与用于估计方程（4）的批次中的样本数量成二次方式地增长，这使得具有估计的成本与维度的数量成二次方，这使得它非常不适用于高维问题。实际上，对于像64x64图像那样标准的东西，我们需要大小至少为4096的小型号（不考虑[19]的范围内的常数，这将使这个数字大得多）和每次迭代的总成本40962，结束使用标准批量大小为64时，比GAN迭代多5个数量级

  话虽如此，这些数字对于MMD来说可能有点不公平，因为我们将GAN的经验样本复杂性与MMD的理论样本复杂性进行比较，后者往往更糟糕。 然而，在最初的GMMN论文[10]中，他们确实使用了1000的小批量，比标准的32或64大得多（即使这是在二次计算成本中产生的）。 虽然具有线性计算成本的估计值是样本数量的函数[5]，但它们具有更差的样本复杂性，据我们所知，它们尚未应用于GMMN等生成环境中。

  在另一个伟大的研究领域，[14]的最近的工作探讨了在受限玻尔兹曼机器学习离散空间的背景下使用Wasserstein距离。 乍一看动机可能看起来很不一样，因为流形设置仅限于连续空间，而在有限的离散空间中，弱和强拓扑（分别是W和JS的拓扑）会重合。然而，最后还有更多的共同点而不是关于我们的动机。我们都希望以一种利用底层空间几何形状的方式比较分布，而Wasserstein允许我们做到这一点。

  最后，[3]的工作显示了计算不同分布之间的Wasserstein距离的新算法。 我们相信这个方向非常重要，也许可能会导致评估生成模型的新方法。

6.结论

我们引入了一种算法，我们认为WGAN是传统GAN训练的替代方案。 在这个新模型中，我们展示了我们可以提高学习的稳定性，摆脱模式崩溃等问题，并提供有用的调试和超参数搜索的有意义的学习曲线。 此外，我们表示相应的优化问题是合理的，并提供了广泛的理论工作，突出了与分布之间的其他距离的深层联系。