OpenCV-Python中cv2.fitEllipse的(a,b)和angle究竟表示什么？

目录

前言

一，a，b的理解

二，angle的理解

2.1 angle思路一

2.2 angle思路二       

三，有趣的cv2.ellipse

四，结论

五，代码

---

前言

首先来看一段代码

ellipse = cv2.fitEllipse(cnt)

#(x, y), (a, b), angle = cv2.fitEllipse(cnt)
#ellipse =  [ (x, y) , (a, b), angle ]

这是网上大部分给出的解释：
ellipse = cv2.fitEllipse(cnt)
        其中 cnt 代表了一组轮廓点，一般常采用cv2.findContours（）函数所返回的轮廓点（也就是一组点集）
        返回值：ellipse = [ (x, y) , (a, b), angle ]
                    （x, y）代表椭圆中心点的位置
                    （a, b）代表长短轴长度，应注意a、b为长短轴的直径，而非半径
                      angle  代表了中心旋转的角度
        但是，a究竟表示的是短轴，还是长轴，b究竟表示的是短轴还是长轴，angle表示的旋转角度是怎么计算的，解释的并不是很清楚。
        最近，我在求cv2.fitEllipse拟合的椭圆边与椭圆长轴和短轴的交点的时候，感觉这3个参数的理解比较的绕，所以我将我的思路记录下来，与大家分享一下。这只是我的理解，如有问题，请指正。

一，a，b的理解

首先看两组对比图

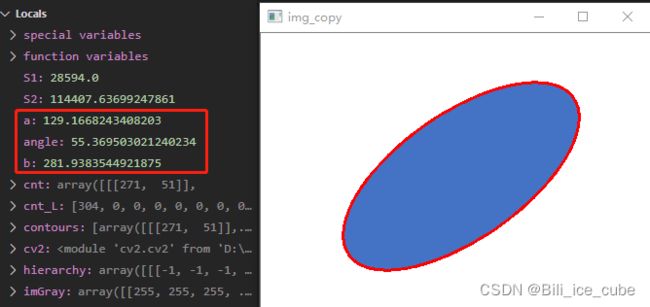
第一组对照

图一  短轴竖直，长轴水平的椭圆

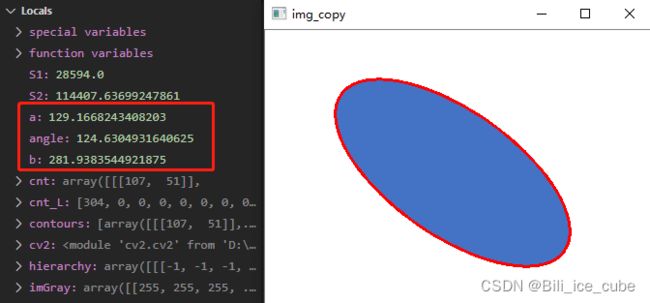
图二  长轴竖直，短轴水平的椭圆

第二组对照

图三  长轴向右倾斜

图四  长轴向左倾斜

        通过两组对照，我们可以看出无论椭圆是怎么样放置的，获得的a均小于b，也就证明了a的值一定是短轴的直径，b的值一定是长轴的直径。 

二，angle的理解

2.1 angle思路一

        通过观察上述第一组对照组，我们可以初步判断，angle可能是短轴与水平轴的夹角。将这结论带入到第二对照组，找到短轴a，结合以前学习的函数知识，旋转的角度应该是按照逆时针方向为正，发现图三和图四均不符合图一图二的结论，反而感觉angle是表示长轴与水平轴的夹角。
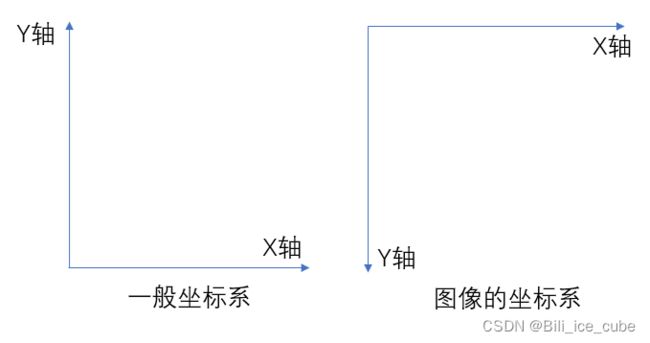
        注意现在是在图像方面，它的坐标系和平时的坐标系不同。

        所以我认为旋转角度应该是以顺时针旋转为正。angle表示短轴与水平轴的夹角。

2.2 angle思路二       

        但是有人就有疑问了，那我如果是先看第二组对照组的图片，理解思路就不一样了撒。而且第一组对照组的椭圆太特殊了，在实际的项目中很难遇到，所以就不会去关注了。如果只看图三和图四，我就有两种理解方式。

1. angle是表示长轴与水平轴的夹角，逆时针为正。
2. angle是表示短轴与水平轴的夹角，顺时针为正。

        感觉两种理解都是对的，但是真相只有一个！请看下面的图片。

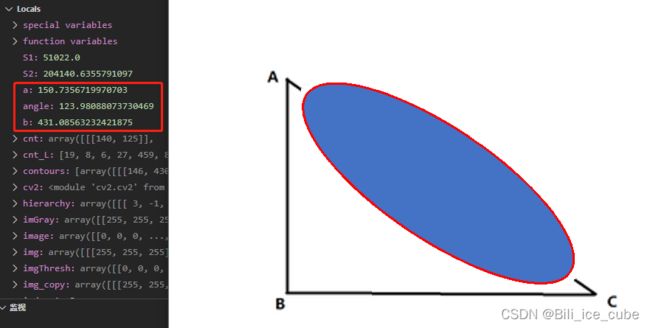
        椭圆的背后是一个30度的直角三角形，角ACB是30度，如果按照上述的理解一来看，angle应该是150度左右。但是现在angle输出的是123左右。说明理解二是正确的。

        补充：这里angle是输出的角度，不能直接三角函数（sin，cos，tan...），需要配和math.radians一起用。

import math

angle = 30
print("angle为30度，sin30度的值为" + str(math.sin(math.radians(angle))))

三，有趣的cv2.ellipse

          在总结这些内容时，我还发现了一个有趣的地方。大家可以先看看这篇博文：cv2.fitEllipse函数详解：ellipse参数并根据参数计算出椭圆焦点坐标_qq1406433326-CSDN博客_ellipse函数的参数cv2.fitEllipse函数详解：ellipse参数并根据参数计算出椭圆焦点坐标最近因为用到了这个函数，所以就趁着这个机会，好好顺顺，做下记录。ellipse = cv2.fitEllipse(cnt)#(x, y), (a, b), angle = cv2.fitEllipse(cnt)#ellipse = [ (x, y) , (a, b), angle ]ellipse 为元组类型，其里面的参数为：（x, y）代表椭圆中心点的位置（a, b）代表长短轴长度，应注意a、b为长短https://blog.csdn.net/qq_33950926/article/details/111409635        当作者在使用cv2.ellipse()这个函数时，得到的椭圆，不符合我上面的理解。经过代码的验证，我发现这位博主，在给函数中输入的a表示长轴，b表示短轴。而我前面下的结论里，我们使用的cv2.fitEllipse()默认获得的a表示短轴，b表示长轴，所以我认为angle和a，b的大小是有关系的。     

四，结论

        1. cv2.fitEllipse()函数输出的（a，b），其中a的值一定是短轴的直径，b的值一定是长轴的直径。 

        2. 不管是cv2.fitEllipse()函数还是cv2.ellipse()函数，在判断angle时：首先，看长短轴的第一个参数。
        如果第一个参数（a）是长轴，那angle是表示长轴与水平轴的夹角，顺时针为正。
        如果第一个参数（a）是短轴，那angle是表示短轴与水平轴的夹角，顺时针为正。

        3. angle是输出的角度，不能直接使用三角函数（math.sin，math.cos，math.tan...），需要配和math.radians一起用。

五，代码

import cv2
import numpy as np
from matplotlib import pyplot as plt
import math


def my_imshow(img, name):  #显示图片
    cv2.namedWindow(
        name,
        cv2.WINDOW_AUTOSIZE + cv2.WINDOW_KEEPRATIO + cv2.WINDOW_GUI_EXPANDED)
    cv2.imshow(name, img)
    return


img = cv2.imread("004_TOUSHI\\test (5).jpg", 3)  #读入图片
# my_imshow(img, "img")
imGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  #灰度图
# my_imshow(imGray, "imGray")
ret, imgThresh = cv2.threshold(imGray, 127, 255, cv2.THRESH_BINARY_INV)  #二值化处理
# my_imshow(imgThresh, "imgThresh")

image, contours, hierarchy = cv2.findContours(
    imgThresh, cv2.RETR_TREE,
    cv2.CHAIN_APPROX_SIMPLE)  #contours为轮廓集，可以计算轮廓的长度、面积等
# my_imshow(image ,"image")

#找出最大的轮廓
index_1 = 0
cnt_L = [0] * 100
for cnt in contours:
    cnt_L[index_1] = len(cnt)
    index_1 = index_1 + 1
max_cnt = np.argsort(cnt_L)[99]

#拟合椭圆
img_copy = img.copy()
for cnt in contours:
    if cnt_L[max_cnt] == len(cnt):
        # 最小外接圆
        (x_Circle, y_Circle), radius = cv2.minEnclosingCircle(cnt)
        print("外接圆的半径" + str(radius) + "\t" + "外接圆的中心点" + str(x_Circle) + "," +
              str(y_Circle))

        #cv2.fitEllipse这个函数是真的坑
        (x_Ellipse, y_Ellipse), (a, b), angle = cv2.fitEllipse(cnt)
        print("椭圆的短轴和短轴直径分别为" + str(a) + "和" + str(b) + "\t" + "外接圆的中心点为(" +
              str(x_Ellipse) + "," + str(y_Ellipse) + ")\t" + "椭圆的旋转角度为" +
              str(angle))

        #判断是否为椭圆
        S1 = cv2.contourArea(cnt)
        S2 = math.pi * a * b
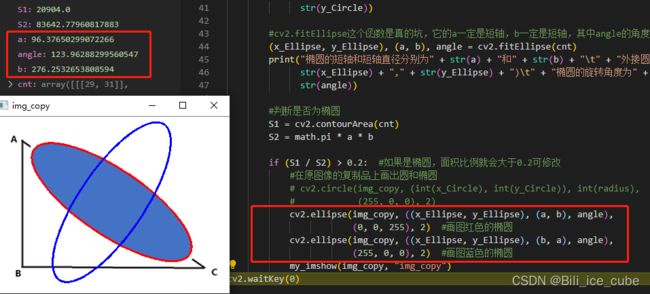
        if (S1 / S2) > 0.2:  #如果是椭圆，面积比例就会大于0.2可修改
            cv2.ellipse(img_copy, ((x_Ellipse, y_Ellipse), (a, b), angle),
                        (0, 0, 255), 2)  #画图红色的椭圆
            cv2.ellipse(img_copy, ((x_Ellipse, y_Ellipse), (b, a), angle),
                        (255, 0, 0), 2)  #画图蓝色的椭圆
            my_imshow(img_copy, "img_copy")
cv2.waitKey(0)

---

        本文只是我初步的理解，真正的涵义只有看了源码才知道。我还没找到源码，如果有大佬知道真正的涵义，欢迎在评论区分享。
        如果本文对你有帮助，麻烦留下一个免费的赞！！！(～￣▽￣)～