遗传算法求旅行商问题Java代码_用遗传算法解决旅行商问题(附源代码)
用遗传算法解决旅行商问题(附源代码)
最近心血来潮,重新拾起大学毕业设计时研究过的遗传算法。去年做毕业设计时还觉得遗传算法是一种多么神秘的算法,但是今天看来,遗传算法也就和冒泡排序算法差不多,都是通用的算法,只不过遗传算法实现起来稍微复杂一点而已。
我曾经被遗传算法的名字所疑惑,还以为遗传算法会改变程序的形态,使得程序就好像生物一样进化,过了几天去看程序已经变得连编写程序的人都认不出来了,汗!大二时的幼稚想法。
遗传算法其实是一种求函数极值的随机搜索算法,但它又不是毫无规则地随机搜索,而是基于一种假设:假设函数值的分布是有一定的连续性的,换句话说函数的极值出现在一个较优值附近的概率要大于出现在一个较差值附近的概率。基于这个假设,遗传算法总是以较大概率保留较优值所代表的搜索方向,而以较低概率保留较差值所代表的搜索方向。这并不是说不去搜索较差值的附近区域,只是搜索的概率较低而已。这个思想与模拟退火算法相似,对于能量较高的系统状态,程序仍然以一定的概率接受,只不过这个概率小于1。
遗传算法的局部搜索能力较强,但是很容易陷入局部极值,毕业设计的时候曾经认为只要增加变异概率就可以跳出局部极值,还美其名曰自适应,现在想想这种想法是错误的:虽然增加变异概率可以搜索到远离当前极值的点,但是新点的值往往不能和当前保留下来的较优值相提并论,因为这些较优值都是经过千百代的进化而存留下来的,于是远离当前极值的点往往在两到三代以内就被淘汰掉了。增加变异概率实际上是把遗传算法退化成了一种纯粹的随机搜索,所谓的自适应也无从谈起!
那么如何解决遗传算法容易陷入局部极值的问题呢?让我们来看看大自然提供的方案。六千五百万年以前,恐龙和灵长类动物并存,恐龙在地球上占绝对统治地位,如果恐龙没有灭绝灵长类动物是绝没有可能统治地球的。正是恐龙的灭绝才使灵长类动物有了充分进化的余地,事实上地球至少经历了5次物种大灭绝,每次物种灭绝都给更加高级的生物提供了充分进化的余地。所以要跳出局部极值就必须杀死当前所有的优秀个体,从而让远离当前极值的点有充分的进化余地。这就是灾变的思想。
下一个问题是什么时候进行灾变,换句话说什么时候局部搜索已经充分了呢?我用了一个灾变倒计数的概念:从500开始递减,每一代递减一次,如果出现了新的最优值,就从新开始计数,如果出现新最优值的时候倒计数递减次数的2.5倍已经超过500则从新的初始值开始倒数。例:初始倒数500,如果倒数到200时出现新最优值,则从(500 - 200) * 2.5 = 750开始从新倒数,下一次如果倒数到100时出现新最优值,则从(750 - 100) * 2.5 = 1625开始倒计数(这里的2.5是一个经验值,可以在全局参数设置里面调整)。也就是说倒计数的长度取决于进化的速度,进化速度越慢倒计数长度越长。如果倒计数完毕还没有新的最优值,就认为局部搜索已经充分,就发生灾变。
基于上诉思想我写了一个程序来计算旅行商问题。我现在终于体会到旅行商问题为什么会这么有名,有很多算法都可以解决旅行商问题,问题描述简单,评价函数也不复杂,问题的解可以直观地显示出来,具有各种如局部极值多等典型的性质,这些都成为算法练兵的好处,可以清晰地比较各个算法的优劣,发现算法的缺陷。可以说旅行商问题就是一个练兵场,一个学校,为算法提供了成长的场所。为算法能够应用到其他复杂领域打好基础。
程序输入是一个文本文件,里面记录了所有城市的坐标,以及最优个体的序列。以一张只有10个城市的地图为例,文本中可能记录了以下内容:
0.604600, 0.592500, 8
0.610500, 0.261400, 3
0.572800, 0.494300, 7
0.153200, 0.983900, 2
0.955700, 0.772000, 0
0.914400, 0.276500, 4
0.998500, 0.484800, 6
0.449800, 0.605300, 5
0.308500, 0.109000, 1
0.364700, 0.060100, 9
表示第一个城市的坐标为0.604600, 0.592500(程序客户区的宽和高为单位1,所有城市的坐标值均在[0.0,0.0] ~ [1.0,1.0]之内),第二个城市坐标为0.610500, 0.261400...依次类推。
后面所跟的整数为最优个体的序列,上述数据表示旅行商应该从第8号城市(0.308500, 0.109000)出发,经过3,7,2,0,4,6,5,1,9号城市,最后又回到第8号城市。
程序的最终目标是求取一个序列,使得旅行商按照这个序列旅行时行程最短。
程序的变异方法是自繁殖变异,有两种:1、随机取两点,逆序这两点间的序列。2、随机把一个城市转移到另一个序列位置。
对于一个500个城市的地图,大概在5万代左右发生第一次灾变,用时约6~8分钟,灾变前夕的灾变倒计数初始值已经从800达到2000~20000。可以看到从一次灾变结束到下一次灾变开始,最优值的变化趋势近似呈一条拖拽线,越接近局部极值进化速度越慢,这也说明灾变倒计数的策略是正确的。
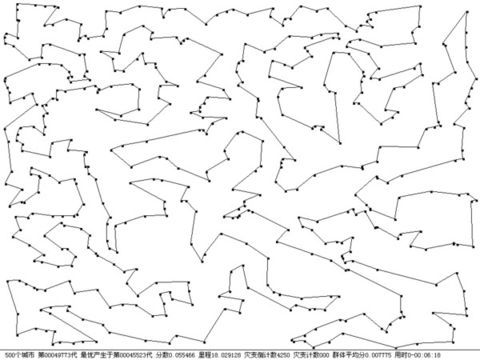
下面是一次试验的数据统计:程序运行两个小时,进化到一百万代,发生了16次灾变,最优个体产生于第606722代,属于第11个进化周期,总行程长度为17.164006,第一次灾变发生在第49773代,第一次灾变前最优个体产生于第45523代,总行程长度为18.029128。
图1 最佳路线图
图2 第一次灾变前的最佳路线
分析最优分趋势图
图3 第一次灾变前的最优分趋势图
图4 最后一次灾变前的最优分趋势图
在每个进化周期内最优分图形基本呈拖拽线形状,可以看到多数进化周期已经没有进化速度,说明局部搜索已经充分,少数进化周期在发生灾变时还有明显进化速度,这是因为这些周期恰好进入一个比较长的停滞期时被程序认为局部搜索充分了,停滞期的出现根随机数有关,个人认为应该可以通过调节灾变初始值和灾变倍增值解决。
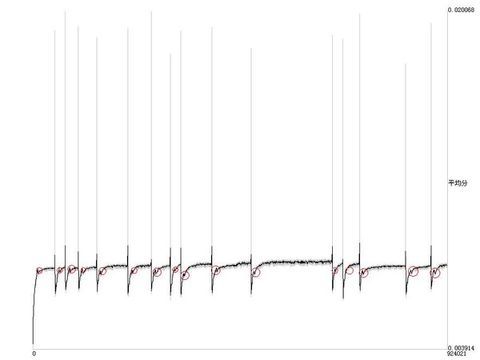
分析平均分趋势图
图5 第一次灾变前的平均分趋势图
图6 最后一次灾变前的平均分趋势图
可以看到每次分生灾变后群体平均分会达到一个较大的值,然后迅速下降,再慢慢上升。这说明旅行商问题的局部极值非常多,极值附近解的分数要远远低于整个解空间的平均分,这主要是因为一个较优解的进行一次变异后生成的子女绝大部分都是畸形的分数很低的个体,由于遗传算法并不放弃这些进化方向,从而影响了群体的平均分。灾变时对整个解空间进行随机搜索,这时的群体平均分可以作为整个解空间平均分的体现,进化一定时间以后,群体迅速陷入到一个特定的局部极值附近,这个时候较优解还没有进化出来,群体中充斥着畸形个体,只有少量比较优秀的个体,所以平均分也随之迅速下降,随后由于优秀个体存活率比较高,群体渐渐被优秀个体统治,群体平均分也开始上升。仔细分析每一个进化周期的平均分趋势图可以发现,在进化的后期群体平均分有一个稳固上升的阶段(这应该是最优个体慢慢排挤其他个体的结果),在此之前都会有一个标志性的少量下挫曲线(如图),还不知道产生这个曲线的原因。
理论上说,保留更多的种子,可以保留更多的搜索方向,搜索的效果应该越好,但是我做了一下对比试验,发现保留1个种子的搜索速度更快,搜索到的极值更优秀,但是这与遗传算法的精髓相违背,困惑中。
程序下载地址:
下面是程序的主要核心代码:
// 变异函数
inline void Variant(GENE & gsource, GENE & gdest, int * ptemp, int size, int varate)
{
static int i;
static int j, k, l, n, m;
static int tmp;
memcpy(gdest.index, gsource.index, sizeof(int) * size);
for(i = 0; i < varate; i++)
{
switch(rand() % 2)
{
case 0:
// 逆序变异
{
j = rand() % size;
k = rand() % size;
if(j == k)
{
k = (k + 1) % size;
}
if(j > k)
{
k += size;
for(l = j; l < j + k - l; l++)
{
n = (j + k - l) % size;
m = l % size;
tmp = gdest.index[m];
gdest.index[m] = gdest.index[n];
gdest.index[n] = tmp;
}
}
else
{
for(l = j; l < j + k - l; l++)
{
tmp = gdest.index[l];
gdest.index[l] = gdest.index[j + k - l];
gdest.index[j + k - l] = tmp;
}
}
}
break;
case 1:
// 转移变异
{
j = rand() % size;
k = 1;//rand() % ((size >> 4) + 1);
if(k == 0)
{
k = 1;
}
l = rand() % (size - k) + 1;
n = (j + k) % size + l > size ? size - (j + k) % size : l;
memcpy(ptemp, gdest.index + (j + k) % size, n * sizeof(int));
if(n < l)
{
memcpy(ptemp + n, gdest.index, (l - n) * sizeof(int));
}
n = j + k > size ? size - j : k;
memcpy(ptemp + l, gdest.index + j, n * sizeof(int));
if(n < k)
{
memcpy(ptemp + l + n, gdest.index, (k - n) * sizeof(int));
}
m = k + l;
n = j + m > size ? size - j :m;
memcpy(gdest.index + j, ptemp, n * sizeof(int));
if(n < m)
{
memcpy(gdest.index, ptemp + n, (m - n) * sizeof(int));
}
}
break;
default:
break;
}
}
}
// 辅助线程
UINT CCityMap::ThreadProc( LPVOID pParam )
{
CCityMap * pClass = (CCityMap *)pParam;
if(pClass->m_iCityNum <= 1)
{
return 0;
}
srand((UINT)time(NULL));
pClass->m_bCompute = true;
pClass->ReadSetting();
static int i, j;
static GENE tgene;
static int bullet;
static int totalBullet;
static int maxCountdown = CM_JUMP_COUNTDOWN_INIT;
// 分配空间
int num = pClass->m_iCityNum;
int * ptmp = new int[num];
int commSize = CM_SEED_NUM * (1 + CM_CHILDREN_NUM);
GENE * comm = new GENE[commSize];
for(i = 0; i < commSize; i++)
{
comm[i].index = new int [num];
comm[i].mark = 0.0;
}
// 生成初始群落
CTime tstart = CTime::GetCurrentTime();
CTime tnow;
pClass->m_i64GenNum = 1;
pClass->m_iJumpCount = 0;
memcpy(comm[0].index, pClass->m_piBestIndex, sizeof(int) * num);
pClass->Mark(comm[0]);
pClass->QuadrangleOptimise(comm[0]);
pClass->m_dBestMark = comm[0].mark;
pClass->m_i64BestGen = pClass->m_i64GenNum;
double maxMark = comm[0].mark;
int maxIndex = 0;
double totalMark = maxMark;
pClass->m_iJumpCountdown = CM_JUMP_COUNTDOWN_INIT;
for(i = 1; i < CM_SEED_NUM; i++)
{
Variant(comm[0], comm[i], ptmp, num, pClass->m_iJumpCountdown);
pClass->Mark(comm[i]);
totalMark += comm[i].mark;
if(maxMark < comm[i].mark)
{
maxMark = comm[i].mark;
maxIndex = i;
}
}
// 移动最优基因
if(maxIndex != 0)
{
tgene.index = comm[0].index;
tgene.mark = comm[0].mark;
comm[0].index = comm[maxIndex].index;
comm[0].mark = comm[maxIndex].mark;
comm[maxIndex].index = tgene.index;
comm[maxIndex].mark = tgene.mark;
maxIndex = 0;
pClass->QuadrangleOptimise(comm[0]);
maxMark = comm[0].mark;
memcpy(pClass->m_piBestIndex, comm[0].index, sizeof(int) * num);
pClass->m_dBestMark = maxMark;
pClass->m_i64BestGen = pClass->m_i64GenNum;
}
int indNum = CM_SEED_NUM;
pClass->m_dAVGMark = (totalMark) / indNum;
pClass->m_pMaxTrendLine->Clear();
pClass->m_pAVGTrendLine->Clear();
pClass->m_pMaxTrendLine->AddValue(maxMark);
pClass->m_pAVGTrendLine->AddValue(pClass->m_dAVGMark);
// 开始进化
while(!pClass->m_bKillMsg)
{
totalMark = 0.0;
// 变异
for(i = 0; i < CM_SEED_NUM; i++)
{
totalMark += comm[i].mark;
for(j = 0; j < CM_CHILDREN_NUM; j++)
{
Variant(comm[i], comm[indNum], ptmp, num, 1);
pClass->Mark(comm[indNum]);
totalMark += comm[indNum].mark;
if(maxMark < comm[indNum].mark)
{
maxMark = comm[indNum].mark;
maxIndex = indNum;
}
indNum++;
}
}
pClass->m_dAVGMark = (totalMark) / indNum;
pClass->m_pAVGTrendLine->AddValue(pClass->m_dAVGMark);
pClass->m_pMaxTrendLine->AddValue(maxMark);
// 移动最优基因
if(maxIndex != 0)
{
tgene.index = comm[0].index;
tgene.mark = comm[0].mark;
comm[0].index = comm[maxIndex].index;
comm[0].mark = comm[maxIndex].mark;
comm[maxIndex].index = tgene.index;
comm[maxIndex].mark = tgene.mark;
maxIndex = 0;
if(maxMark > pClass->m_dBestMark)
{
memcpy(pClass->m_piBestIndex, comm[0].index, sizeof(int) * num);
pClass->m_dBestMark = maxMark;
pClass->m_i64BestGen = pClass->m_i64GenNum;
}
int forcastCountdown = int((maxCountdown - pClass->m_iJumpCountdown) * CM_JUMP_COUNTDOWN_INC);
if(forcastCountdown > maxCountdown)
{
maxCountdown = forcastCountdown;
}
pClass->m_iJumpCountdown = maxCountdown;
}
else
{
pClass->m_iJumpCountdown--;
if(pClass->m_iJumpCountdown <= 0)
{
pClass->QuadrangleOptimise(comm[0]);
if(maxMark < comm[0].mark)
{
pClass->m_iJumpCountdown = maxCountdown;
maxMark = comm[0].mark;
if(maxMark > pClass->m_dBestMark)
{
memcpy(pClass->m_piBestIndex, comm[0].index, sizeof(int) * num);
pClass->m_dBestMark = maxMark;
pClass->m_i64BestGen = pClass->m_i64GenNum;
}
}
else
{
if(CM_IMG_LOG)
{
// 保存当前屏幕图像为文件,作为日志
pClass->m_iJumpCountdown = maxCountdown;
static CString fileName;
fileName.Format("%03d.bmp", pClass->m_iJumpCount);
pClass->SaveAsImage(fileName);
}
srand((UINT)time(NULL));
maxCountdown = CM_JUMP_COUNTDOWN_INIT;
pClass->m_iJumpCountdown = maxCountdown;
// 已经陷入局部最优,灾变
pClass->m_iJumpCount++;
Variant(comm[0], comm[0], ptmp, num, 20);
pClass->Mark(comm[0]);
maxMark = comm[0].mark;
for(i = 1; i < CM_SEED_NUM; i++)
{
Variant(comm[0], comm[i], ptmp, num, 20);
pClass->Mark(comm[i]);
totalMark += comm[i].mark;
if(maxMark < comm[i].mark)
{
maxMark = comm[i].mark;
maxIndex = i;
}
}
// 移动最优基因
if(maxIndex != 0)
{
tgene.index = comm[0].index;
tgene.mark = comm[0].mark;
comm[0].index = comm[maxIndex].index;
comm[0].mark = comm[maxIndex].mark;
comm[maxIndex].index = tgene.index;
comm[maxIndex].mark = tgene.mark;
maxIndex = 0;
}
indNum = CM_SEED_NUM;
}
}
}
// 轮盘赌
totalMark -= comm[0].mark;
totalBullet = 0;
for(i = 1; i < indNum; i++)
{
comm[i].killRate = int(10000.0 * comm[i].mark / totalMark);
totalBullet += comm[i].killRate;
}
while(indNum > CM_SEED_NUM)
{
bullet = rand() % totalBullet;
for(i = 1; i < indNum; i++)
{
if(bullet <= comm[i].killRate)
{
// 命中
totalBullet -= comm[i].killRate;
tgene.index = comm[indNum - 1].index;
tgene.mark = comm[indNum - 1].mark;
tgene.killRate = comm[indNum - 1].killRate;
comm[indNum - 1].index = comm[i].index;
comm[indNum - 1].mark = comm[i].mark;
comm[indNum - 1].killRate = comm[i].killRate;
comm[i].index = tgene.index;
comm[i].mark = tgene.mark;
comm[i].killRate = tgene.killRate;
indNum--;
break;
}
else
{
bullet -= comm[i].killRate;
}
}
}
pClass->m_i64GenNum++;
tnow = CTime::GetCurrentTime();
pClass->m_tsTimeUsed = tnow - tstart;
}
// 释放空间
for(i = 0; i < commSize; i++)
{
delete [] comm[i].index;
comm[i].index = NULL;
}
delete [] comm;
comm = NULL;
tgene.index = NULL;
pClass->m_bCompute = false;
return 0; // thread completed successfully
}