鸽子学统计

---

第一部分 基础统计

0 统计学的目的和本质

0.1 随机变量

随机变量（random variable）就是随机事件的数量化，随机事件不论与数量是否直接有关，都可以数量化，即都能用数量化的方式表达：

• 随机变量表示随机试验各种结果的实值；

• 随机事件数量化的好处是可以用数学分析的方法来研究随机现象。例如某一时间内公共汽车站等车乘客人数，电话交换台在一定时间内收到的呼叫次数，灯泡的寿命等等，掷硬币正面向上的次数等等，都是随机变量的实例。

如果微积分是研究变量的数学，那么概率论与数理统计是研究随机变量的数学。

• 研究一个随机变量，不只是要看它能取哪些值，更重要的是它取各种值的概率如何！！！

这句就是本文的核心内容，这篇文章里的所有概念都在是描述一件东西，那就是概率！概率！概率！

0.2 统计分析的目的

统计分析是指收集数据、整理分析数据和由数据得出结论的一组概念、原则和方法。

• 目的：

  1. 分析历史变化特征，总结历史变化规律。
  2. 预测未来

• 手段：

  1. 描述性统计：利用表格、图形或者数据(数值特征)来展示和刻画数据中的信息(表面特征)，只能观测数据的分布情况，而不能得到数据背后的真实特征。
  2. 推断性统计：利用样本获得数据对总体的性质进行估计或者检验。即利用高级统计方法对描述性统计进行检验，统计的性质通常用概率模型刻画。

0.3 统计学的本质

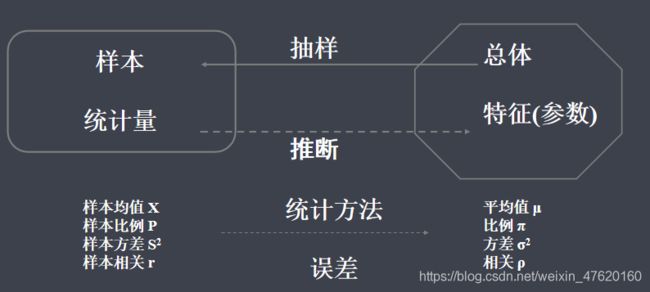
人工智能有三大领域：统计学、机器学习和深度学习，统计学与其他两个领域最大的区别就是通过抽样推断总体特征。

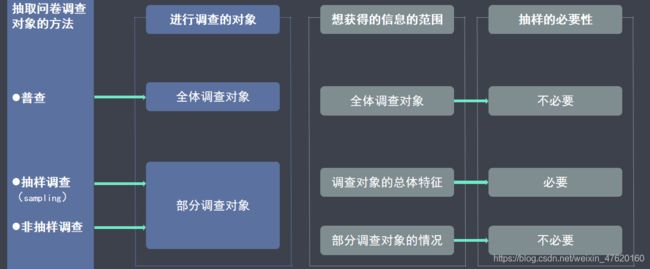
抽样：为了了解全体调查对象的倾向，需要以抽样的方式统计性地抽取一部分调查对象，然后根据样本中所包含的信息对总体的状况进行估计和推算。

1 描述统计

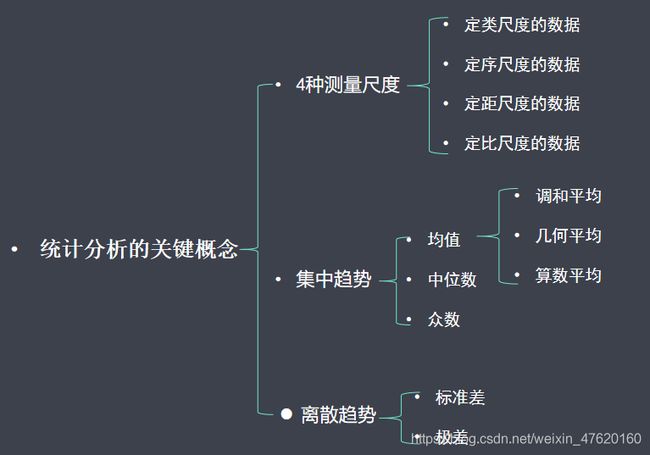
1.1 变量的测量尺度分类

• 人文社科的分类：

  1. 定类变量(nominal)：例如性别、喜欢的艺人

     仅有分类功能。

  2. 定序变量(ordinal)：例如年级、喜欢的艺人的排名

     具备分类、排序功能。

  3. 定距变量(scale)：例如温度

     具备定序和定类功能的同时多了个加减的功能，但是不具备乘除功能。

  4. 定比变量(scale)：例如体重、身高、年龄、年收入等；

     具备以上功能的同时增加了乘除功能。

• 工科或其他行业分类：

  1. 定类与定序合称分类变量

     分类变量的描述统计方法只能用频次统计。

  2. 定距和定比合称连续变量

     对于连续变量的描述统计方法既可以用频次统计，也用标准差、均值。

1.2 均值

• 算数平均数：包括加权平均数。
• 几何平均数：多用于平均比率和平均速率。在计算多年的平均增长率时，还会遇见复增长率。
• 调和平均数：可能用在数据中较多数值在最小值附近，原因可能是调和平均值比算数平均值和几何平均值小。
• 调整平均数：是指在上限值和下限值中去掉一定比例（通常5%）的数据后剩下数据的算数平均值。

tips:数据分析算出来的均值要有代表性，要删除异常值，相对占比较少的值就是异常值。

1.3 众数和中位数

• 中位数：当一组序列数据之间差异较大时，导致平均值代表性较弱，可通过中位数来表示数据的集中趋势。平均值和中位数通常应用在连续变量中，即数值型变量。

• 众数：即可以应用在连续变量，也可以应用在分类变量中。

1.4 极差和标准差

• 衡量数据的离散趋势，数据的离散趋势代表了数据中包含的信息量，离散的程度越高，数据解释起来越复杂。
• 如果希望比较两组数据的离散趋势，不能直接比较两组数据的标准差，因为两组数组的数量和均值不同。通常选用离散系数来比较，离散系数等于标准差除以均值。
• 标准差计算公式中有的除以N，有的除以N-1，当计算总体数据标准差时除以N，通过样本数据计算总体标准差时除以N-1。

1.5 偏度和峰度

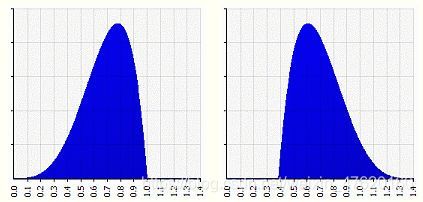
• 偏度（Skewness）可以用来度量随机变量概率分布的不对称性。

  • 偏度的取值范围为(-∞,+∞)；
  • 当偏度<0时，概率分布图左偏；
  • 当偏度=0时，表示数据相对均匀的分布在平均值两侧，不一定是绝对的对称分布；
  • 当偏度>0时，概率分布图右偏。
    

• 例如上图中，两个概率分布图都是均值=0.6923，标准差=0.1685的，但是他们的形状是不一样的，左图偏度=-0.537，形状左偏，右图偏度=0.537，形状右偏。

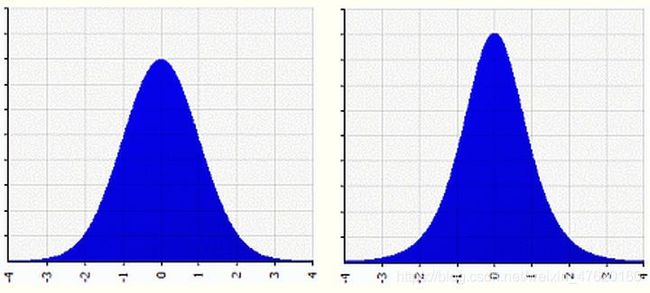
• 峰度（Kurtosis）可以用来度量随机变量概率分布的陡峭程度。

  • 峰度的取值范围为[1,+∞)，完全服从正态分布的数据的峰度值为 3，峰度值越大，概率分布图越高尖，峰度值越小，越矮胖。
    

• 例如上图中，左图是标准正太分布，峰度=3，右图的峰度=4，可以看到右图比左图更高尖。

• 通常我们将峰度值减去3，也被称为超值峰度（Excess Kurtosis），这样正态分布的峰度值等于0，当峰度值>0，则表示该数据分布与正态分布相比较为高尖，当峰度值<0，则表示该数据分布与正态分布相比较为矮胖。

1.6 小结

2 总体推断

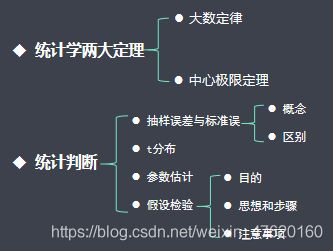
2.1 大数定律和中心极限定理

• 大数定律：样本n越大，样本均值几乎必然等于均值。
• 中心极限定理：当样本量N逐渐趋于无穷大时，N个抽样样本的均值的频数逐渐趋于正态分布。

2.2 抽样误差和标准误

• 抽样误差

  由个体变异产生的、抽样造成的样本统计量与总体参数的差别。原因：

  • 抽样
  • 个体差异

• 标准误

  表示样本统计量抽样误差大小的统计量。

2.3 T分布

t分布只有一个参数，即自由度v。当自由度不同时，曲线的形状不同；当自由度趋向无穷大时，t分布趋近标准正态分布。

• Z值转换公式：用来将t分布转换为（0,1）z分布，又称为标准化，或者Z值标准化。

• Z=(xi-x)/s，用于判断哪些数值为异常值，Z值绝对值大于3为异常值，大于5为极端值。

2.4 参数估计

定义：用样本统计量推断总体参数。

点估计：用相应样本统计量直接作为总体参数的估计值。
区间估计：按预先给定的概率所确定的包含未知总体参数的一个范围。

tips:注意总体标准差是否已知和样本量n的大小。总体标准差未知且样本量较小，按t分布估计。样本量较大，按z分布估计。

• 置信度：

  T=1.65 对应90%的置信度

  T=1.98 对应95%的置信度

  T=2.58 对应99%的置信度

2.5 假设检验

基本思想：小概率反证法： 利用小概率反证法思想，从问题对立面（H0）出发间接判断要解决的问题（H1）是否成立。然后在H0成立的条件下计算检验统计量，最后得到P值来判断。当P值小于预先设定的显著性水平a时，就属于小概率事件。根据小概率事件的原理：小概率事件在一次抽样中发生的可能性很小，如果发生了，则有理由怀疑原假设H0，认为其对立面H1是成立的。

• 步骤：

  1. 定义H0和H1，H0通常是定义两个变量之间不存在相关性或者没有显著差异
  2. 选择合适的检验方法，计算统计量
  3. 根据统计量计算概率P值
  4. P值与显著性水平0.05对比，P<0.05，拒绝原假设H0，接受H1，反之则接受H0。

• 第Ⅰ类错误和第 Ⅱ 类错误：

  • 第Ⅰ类错误（alpha类错误）：原假设是正确的，但拒绝了原假设（弃真）。
  • 第 Ⅱ 类错误（beta类错误）：原假设是错误的，但没有拒绝原假设（存伪）。

2.6 小结

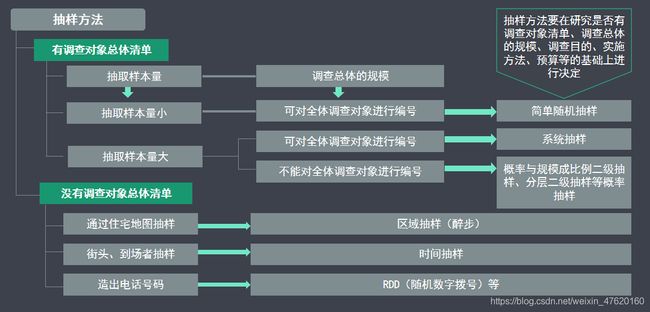
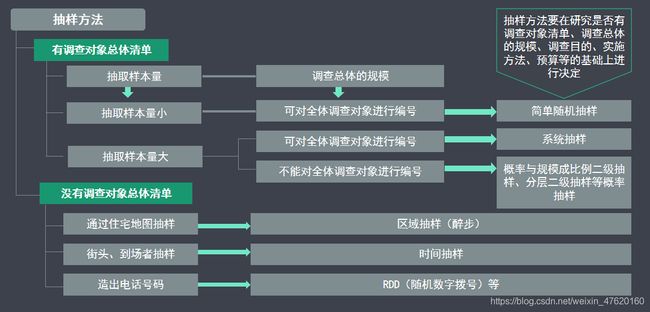
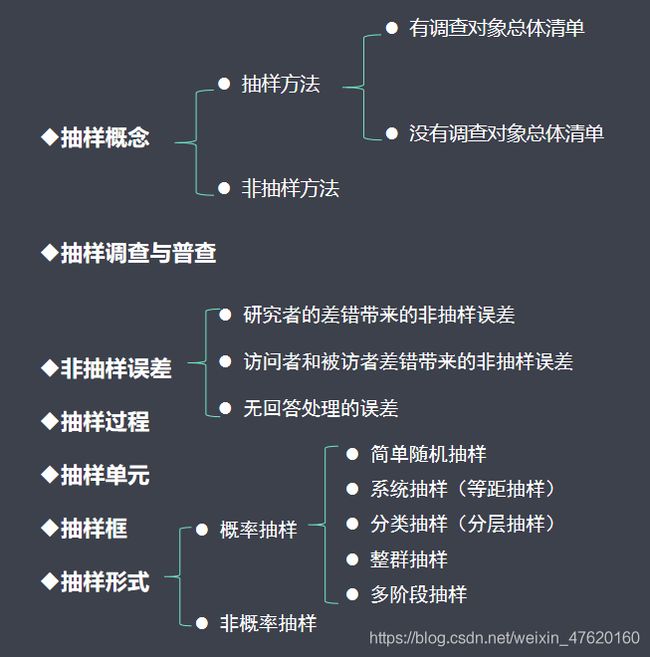
3 抽样方法

3.1 抽样的概念和意义

抽样：指在不能进行全数调查时，为了推测总体的倾向，抽取真实地代表调查总体的调查对象。

• 是否需要抽样：

  

• 抽样方法：

  

• 非抽样方法：

  

3.2 抽样误差和非抽样误差

• 抽样误差

  抽样误差是指由于随机抽样的偶然因素使样本各单位的结构不足以代表总体各单位的结构，而引起抽样指标和全局指标的绝对离差。

• 非抽样误差

  • 非抽样误差是指除抽样误差外，由于人为的差错引起的误差，也叫偏差
  • 问题的定义、处理问题的途径、量表问卷中问题的设计、访问的方法、实施的质量控制、数据处理和分析的失当都会造成非抽样误差
  • 非抽样误差包括研究员、访问员、被访者三方面的误差
  • 为确保调查结果的准确性，应该消除非抽样误差，至少应尽可能使之最小化

3.3 抽样过程及相关概念

• 抽样过程：

  

• 抽样单元：为了便利地实现随机抽样，常常把总体划分为有限个互不重叠的部分，每一部分叫做一个抽样单元。

  例如：XX省XX市XX区XX街道XX居委会

• 抽样框：抽样框是包含全部抽样单元的资料。

  • 一般说来，普查可以提供抽样框资料
  • 表现形式名单、地图、统计年鉴等
  • 很多时候，很难获得完整的抽样框资料

3.4 抽样样式与非概率抽样

• 概率抽样：
  • 等概率抽样—所有的样本单位所出现的机会是相同的。
  • 不等概率抽样—可以计算每个样本单位所出现的概率。
  • 按照随机/概率规律的原则，从总体中抽取样本。可以对总体进行推断。
• 非概率抽样：
  • 所有的样本单位所出现的机会是不确定的。
  • 不能计算每个样本单位所出现的概率，因为选择样本的方法是非随机的。
  • 方便抽样：利用会议、展览、商场、街头抽样；报刊问卷调查，网络问卷。
  • 判断抽样：依据研究者主观判断，选取可代表总体的个体作为样本。
  • 配额抽样：按照调查对象的某种属性或特征，将总体中所有个体分类，然后按照一定比例分别抽取样本。配额抽样有可能接近概率抽样的结果。前提是各类群同质，无需随机抽样；类型划分合理；配额符合总体中各类型的分布。
  • 滚雪球抽样：又称裙带抽样、推荐抽样，是一种在稀疏总体中寻找受访者的抽样方法。

3.5 简单随机抽样和系统抽样

• 简单随机抽样：
  • 简单抽样方法是指对所有调查对象编上一连串的号码，据此从名册中进行随机抽样的方法。
  • 是在可以对所有调查对象进行编号的情况下所使用的抽样方法。通过查随机数表等的方法，随机地抽取调查对象的号码。
  • 虽然简单抽样方法可以均匀地抽取代表总体的样本，是一种精度较高的方法，但由于样本量越多查随机数表的次数也越多，进行起来较为繁琐。
  • 当研究总体不太大，或总体单元的元素有完备的名单是，简单随即抽样非常适用。
• 系统抽样(等距抽样)：
  • 系统抽样方法先求出抽样间隔值 （为名册登记人数÷抽取人数所得的值舍去小数点后面数字的整数），接着，在这个范围内选择一个随机数作为起始号码。起始号码加抽样间隔值，所对应的即为样本。进而，反复地在这个值的基础上加上抽样间隔值，以抽足所有的样本。抽取的样本量多于要求的样本量时，使用简单抽样方法从中抽取需要剔除的样本。
  • 另外，系统抽样方法的规则较简单，但如果名册是按一定的规律进行登记的话，也会发生问题。例如，员工名册等是按部门单位进行登记的，当每个部门的人数相等，而且按职务大小进行排列时，起始号码为1，如果以部门人数作为间隔，最终选出的将只是部门的头儿。因此，需要弄清楚名册的特征之后再选择抽样的方法。

抽样方法	优点	缺点
简单抽样方法	精度高	费事费时进行调查总体范围广的访问调查时，实施费用多
系统抽样方法	不费事，不费时	精度比简单抽样方法低调查总体清单有规律地排列时，抽取出来的可能只是特定性质的样本（见下例）

3.6 概率与规模成比例抽样(PPS抽样)

• 这是抽样单位在2个以上时的抽样方法，通过缩小区域和调查对象的范围，从大规模的总体中高效率地进行抽样。它是一种使用辅助信息，从而使每个单位均有按其规模大小成比例的被抽中概率的一种抽样方式。
• PPS 抽样实际上是整群抽样与简单随机抽样或等距抽样（系统抽样）配合的两阶段抽样。
• PPS 抽样是指按概率比例抽样，属于概率抽样中的一种。是指在多阶段抽样中，尤其是二阶段抽样中，初级抽样单位被抽中的机率取决于其初级抽样单位的规模大小，初级抽样单位规模越大，被抽中的机会就越大，初级抽样单位规模越小，被抽中的机率就越小。就是将总体按一种准确的标准划分出容量不等的具有相同标志的单位在总体中不同比率分配的样本量进行的抽样。

3.7 分层抽样

• 分层原则：层内差异小，层间差异大

• 优点

  • 子总体内的抽样单元之间差异比较小，子样本具有较好的均匀性，可能得到较高精度的估计量
  • 有效消除特殊个体的影响
  • 可对各层的特性加以比较
  • 实施管理方便

• 如何选择分层变量：

  1. 选择与研究主题高度相关的变量，例如研究收入问题时，考虑学历、年龄、性别等影响收入的基本属性。
  2. 成本；分层因素考虑越多，选取的样本量则会越多。例如学历分为高中低，收入分为高中低，性别分为男女，总共18类，每类样本量至少保证30人以上，共540人，成本较高。与研究主题不太相关的因素可以不考虑，或者将因素的分类减少。

3.8 区域抽样

• 概念：在访问调查中，由于居民基本登记名册使用起来不方便，一级抽样选出街区后，在二级抽样中抽取样本（家庭户和个人）时，也有用住宅地图来代替抽样名册的情况。这种将住宅地图用作抽样名册的方法，称为区域抽样。

  区域抽样，用来抽取单门独户的房子、有院子的房子，有车子的房子等家庭户有时也很方便。首先，用从市面上买来的住宅地图通过随机数从中选出一页，接着，随机抽取起始住宅。在住宅地图上定好起始住宅后，预先用箭头按顺时针方向标明访问住宅的路线。抽样间隔定为3～10所住宅。

• 特征：在没有调查对象清单的访问调查中使用

• 优点：没有居民基本登记名册，也可以实施访问调查 ，便于寻找通过外表即可看出是否符合条件的家庭户（有院子的家庭、有车的家庭等）

• 缺点：有可能偏向经常在家的调查对象无法从外表看出是否符合条件和以个人为对象进行调查时，效率低下（访问家庭与调查条件不符，调查对象正在外出等）

3.9 时间抽样

• 概念：时间抽样是指，比如，从50个行人中邀请1人接受调查时所使用的抽样。由于不清楚调查总体的情况，所以不能计算抽样比。但是，只要样本量足够大，并尽量按相等的抽样间隔进行抽样，就可以保证样本的代表性。为了使样本具有代表性，从经验上讲，样本量需要500人以上、最好能达到1000人。
• 如果事先测定好调查地点从周一到周日各天不同时间段的行人数量，对于确定所需的访问员人数、抽样间隔和调查结果回收目标人数会有较大的帮助。例如，如果用不同调查地点的行人数除以调查结果回收目标人数，就能计算出每隔多少人邀请1个人接受访问为好。当事先观察到的不同时间段的行人数，以及不同时间段的回收样本构成和实际情况不相符时，则还要通过“加权”对统计结果进行调整。

3.10 电话号码抽样

作为电话调查所独有的抽样方法，有RDD（Random Digit Dialing ） 和Plus1。

• RDD：通过随机数产生与不同区域正在使用的电话号码位数相等的号码，并据此来造出电话号码的方法 。
• Plus 1：从电话簿数据库中抽出电话号码，在它的最后一位数字加上或者减去1-9的任何一个数字的方法。

无论是RDD还是Plus1 ，由于都用计算机自动拨出生成的电话号码，所以不需要进行人工抽样。也有用印刷版的电话簿进行抽样的方法，但这种方法也存在一个问题，那就是有些电话号码可能会出现空号。

3.11小结

TIPS：概率抽样的时候要思考每个样本被选中的概率是多少，是否一样。

4 非参数检验

4.1 单样本非参数检验

• 非参数检验：是指在总体分布未知或知之甚少的情况下，利用样本数据对总体分布形态等进行推断的方法。由于非参数检验方法在推断过程中不涉及有关总体分布的参数 ，因而得名为“非参数”检验。
• 假设检验的结论：P<0.05，则研究假设成立，反之P>0.05，则研究假设不成立。

4.1.1 卡方检验

• 卡方检验能检验所有类别是否包含相同频率或者用户指定比例一致。

  • 原假设：变量的取值分布与均匀分布（或研究者设定的分布比例）没有显著差异。
  • 研究假设：变量的取值分布与均匀分布（或研究者设定的分布比例）有显著差异。
  • 如果P<0.05，则研究假设成立。

• 卡方检验的重要性:

  • 适用于不知道总体参数的检验，是最常用的一种非参数检验。
  • 当不适用参数检验法时，第一个想到的就是卡方检验。

• 卡方检验的应用场景:

  • 检验一个变量中取值的比例分布是否均匀或者比例分布。

4.1.2 二项式检验

• 二项式检验能检验一个变量取二分类的两个值的概率是否符合设定的概率。
  • 原假设：变量的第一个取值比例与设定比例没有显著差异。
  • 研究假设：变量的第一个取值比例与设定比例有显著差异。
  • 如果P<0.05，则研究假设成立。

4.1.3 K-S检验

• KS检验能检验样本来自的总体中，一个变量的分布是否服从正态分布、均匀分布、泊松分布、指数分布。
  • 原假设：变量来自总体的分布与正态分布（或均匀分布等）没有显著差异，即变量在总体中呈现正态分布。
  • 研究假设：变量来自总体的分布与正态分布（或均匀分布等）有显著差异，即变量在总体中不呈现正态分布。
  • 如果P<0.05，则研究假设成立。

4.1.4 游程检验

• 游程检验能检验一个变量的两个取值出现顺序是否随机。通常是检验随着时间变化而产生的两个数值，出现顺序是否随机。
  • 原假设：变量的两个值出现顺序和随机出现没有差异，即两个值出现是随机的。
  • 研究假设：变量的两个值出现顺序和随机出现有差异，即两个值出现不是随机的。
  • 如果P<0.05，则研究假设成立。

4.2 独立样本非参数检验

• 独立样本：两组不同不重叠的样本，比如男性和女性。

• 独立样本非参数检验能检验在收入、年龄等等分布上是否有差异，即检验不同人群在特定变量取值上是否有差异。

• 原假设：两组来自总体的变量数据在分布上没有差异，即两组数据在该变量的取值上没有显著差异。

注意：比较独立样本的时候，分组变量一定是分类变量，比较变量一定是连续变量

4.3 配对样本非参数检验

• 配对样本：同一组人群在不同时间采集的两组或多组数据；或同一组人群不同身体部位采集的两组或多组数据。

• 配对样本非参数检验能检验同一组人群在不同时间采集的数据是否有差异。

• 原假设：来自总体的同一组人群的两组数据在分布上没有差异，即两组数据在该变量的取值上没有显著差异。

注意：t1、t2是分类变量，比较的变量必须是连续变量

4.4 交叉分析（列联表分析）

• 交易分析能检验两个分类变量是否存在相关性。如果场景中需要对连续变量进行卡方检验，首先需要将连续变量转换为分类变量，如将收入分为低中高收入。

• SPSS操作：

  1. 连续变量转成分类变量的操作：转换 - 重新编码为不同变量。
  2. 如果两个变量都是定类变量，相关系数可以通过卡方检验中“名义”里的四个相关系数；如果两个都是定序变量，则选择“有序”里的四个相关系数。
  3. 如果两个变量中，一个为定类变量，一个为定序变量，相关系数应该选择“名义”中的四个相关系数，因为定序变量可降级为定类变量，定序变量具备定类和定序功能。

• 卡方检验结果解读：

  1. 看卡方统计结果，根据P值判断两个变量是否存在相关性，如P<0.05，则说明两者存在显著相关性。

  2. 看相关系数，判断两者之间的相关性到底有多大。

     我们一般认为：

     相关系数	相关性
     0 - 0.2	较弱相关
     0.2 - 0.4	弱相关
     0.4 - 0.6	一般
     0.6 - 0.8	较强相关
     0.8 - 1	极强相关

  3. 看频次分布，具体分析两者的相关关系是怎样变化的。

5 参数检验

• 当总体分布已知（如总体为正态分布），参数检验可以根据样本数据对总体分布的统计参数进行推断。此时，总体的分布形式是给定的或是假定的，只是其中一些参数的取值或范围未知，分析的主要目的是估计参数的取值，或对其进行某种统计检验。这类问题往往用参数检验来进行统计推断。它不仅仅能够对总体的特征参数进行推断，还能够实现两个或多个总体的参数进行比较 。

• 而非参数统计方法，对变量的分布没有要求。

5.1 T检验

• 目的：在样本中比较连续变量的平均数，以检验均值之间的差异是否大于能被机遇所解释的差异。即：样本均值有差异，总体之间确实存在差异的概率是多少？
• 包括单样本t检验、独立样本t检验、配对样本t检验，都是用来通过样本均值对总体均值的推断检验。
• 适用于小样本的检验方法，当样本较小时（50以下），服从t分布；样本量较大时近似服从正态分布。在实际应用中，主要适用在两组样本的均值比较中。
• 此检验是用来判断一个现象，但是背后原因还需深挖。

5.1.1 单样本T检验

• 用来检验样本中某个连续变量的样本均值与给定的总体均值是否存在差异。

• 用到的变量：一个连续变量。

• 例子：

  • 周岁儿童的平均身高是否为75厘米。

  • 居民平均存（取）款金额是否为2000元。

  • 某工厂用自动打包机打包，每包标准质量为100kg。为了保证生产的正常运行，每天开工后需要先行试机，检查打包机是否有系统偏差，以及时进行调整。某日开工后在试机中共打了9 个包，测得9包的质量（kg）为：99.3、98.7、100.5、101.2、98.3 、99.7、99.5、102.1、100.5。现希望作出判断，明确打包机是否需要进行调整。

• 数据要求：小样本时来自的总体服从正态分布，如果大样本或者是数据收集的时候没有特殊性，可以忽略正态分布的假设。

• 单样本均值检验过程：

  1. 提出零假设： 总体均值与检验值之间不存在显著差异（样本均值所引起的差异是抽样误差引起的）。
     • 原假设：样本来自总体的该变量均值与给定均值之间没有显著差异。
     • 研究假设：样本来自总体的该变量均值与给定均值之间有显著差异。
  2. 选择检验统计量：假设总体分布服从正态分布，方差已知时，构造Z统计量；方差未知时，构造t统计量。
  3. 计算检验统计量观测值和概率P值
  4. 给出显著性水平，并作出决策：
     • 如果该P<0.05，成为了我们所定义的小概率事件（小于等于α水准），则我们怀疑所做的假设不成立，从而拒绝H0。
     • 反之，我们就不能拒绝H0。

5.1.2 独立样本T检验

• 用来检验两组独立样本中某个连续变量的总体均值是否存在差异。

• 用到的变量：一个分类变量（也可以用连续变量分组）和一个连续变量。

• 例子： 某证券公司调查到到散户股民买进、卖出和投资的有关数据，要检验文化程度高的股民和文化程度低的股民各项指标的均值有无不同。

• 数据要求：

  • 样本来自的总体服从正态分布 。
  • 两样本必须相互独立，即：抽取其中一批样本对抽取另一批样本没有任何影响，两组样本的个案数可以不相等。
  • 要求两样本是大样本，小样本则必须来自正态总体。

• 独立样本均值t检验过程：

  1. 提出原假设： 两组独立样本来自的总体在该变量的均值上没有显著差异。
  2. 进行方差齐性检验：在两样本的总体均值方差未知的情况下计算t值。
     • 方差齐性检验：是用来检验不同组的总体方差是否相等。
     • 原假设：两组总体中的方差是相等的。
     • 在一些统计推断的过程，要求进行比较的两组或多组数据的方差相等，即要求方差齐性，如均值比较、方差分析 。
     • 方差齐性检验的方法有Hartley检验、Cochran检验、Bartlett检验和Levene检验，前三者对样本数据有正态分布的要求，但是Levene检验则没有这种要求，也是最常用的一种方法。
  3. 根据t值对应的P值，得出结论。

5.1.3 配对样本均值T检验

• 用来检验同一组样本不同时间/部位/处理条件测量得到的两组数据均值是否存在差异。

• 用到的变量：同一组样本的两个连续变量（其实是针对同一组人群不同时间/部位/处理条件测量得到的两组数据）。

• 例子：某种减肥茶是否有效。

• 数据要求：

  • 两样本数据必须两两配对，即：样本个数相同，个案顺序相同，如减肥茶效果、不同广告形式对销售额的影响。
  • 两总体服从正态分布(小样本情况下)，样本容量>30的情况下，且数据收集是随机的，可以认为服从正态分布。

• 配对样本均值t检验过程：

  1. 提出原假设：两组配对数据之间没有显著差异。
  2. 先求出每对观测值的差，再将差值与总体均数0（如果配对数据没有差异，那总体差值平均数应该是0）作单样本的t检验。

5.2 F检验/方差检验/ANOVA

• 对3个以上的组之间的平均值的差进行比较，从统计学意义上判断是否有显著差异，用来揭示作用于一个因变量的几个分类自变量（称为因素）的主效应和交互效应。

• 用到的变量：自变量既可以是分类变量，也可以是连续变量；因变量必须是连续变量。

• 需在两个前提成立下才能使用：

  1. 变量各总体服从正态分布（数据进行方差检验前需检验分布情况）。
  2. 变量各总体方差相同（数据进行方差检验前需做方差齐性检验）。

• 原理：

  1. 计算组内、组间、随机因素的数据差异程度；
  2. 计算组间数据差异程度占观测变量（因变量）数据总差异的比例，与组内差异、随机因素的差异占比之间的大小关系。
  3. SST=SSA+SSE，SST为观测变量总离差平方和，SSA为组间离差平方和，SSE为组内离差平方和。

5.2.1 方差检验常用术语

• 因素（Factor）: 因素是可能对因变量有影响的变量，一般来说，因素会有不止一个水平，而分析的目的就是考察或比较各个水平对因变量的影响是否相同。

• 水平（Level）: 因素的不同取值等级称作水平，例如性别有男、女两个水平。

• 单元（Cell）: 单元亦称试验单位（Experimental Unit），指各因素的水平之间的每种组合。指各因素各个水平的组合，例如在研究性别（二水平）、血型（四水平）对成年人身高的影响时 ，该设计最多可以有2*4＝8个单元。注意在一些特殊的试验设计中，可能有的单元在样本中并不会出现，如正交设计。

• 元素（Element）:

  • 指用于测量因变量值的观察单位，比如研究职业与收入间的关系，月收入是从每一位受访者处得到，则每位受访者就是试验的元素 。
  • 一个单元格内可以有多个元素，也可以只有一个，甚至没有元素。
  • 注意：元素不一定就等同于受访者个体，例如：
    • 重复测量数据时
    • 以家庭为单位收集资料时

• 均衡（Balance）： 如果在一个实验设计中任一因素各水平在所有单元格中出现的次数相同，且每个单元格内的元素数均相同，则该试验是均衡的，否则，就被称为不均衡。不均衡的实验设计在分析时较为复杂，需要对方差分析模型作特别设置才能得到正确的分析结果。

• 协变量（Covariates）： 指对因变量可能有影响，需要在分析时对其作用加以控制的连续性变量，实际上，可以简单的把因素和协变量分别理解为分类自变量和连续性自变量。当模型中存在协变量时 ，一般是通过找出它与因变量的回归关系来控制其影响。

• 交互作用（Interaction）：

  • 如果一个因素的效应大小在另一个因素不同水平下明显不同，则称为两因素间存在交互作用。当存在交互作用时，单纯研究某个因素的作用是没有意义的，必须分另一个因素的不同水平研究该因素的作用大小。
  • 如果所有单元格内都至多只有一个元素，则交互作用无法进行分析，只能不予考虑。

• 固定因素（Fixed Factor）： 指的是该因素在样本中所有可能的水平都出现了。从样本的分析结果中就可以得知所有水平的状况，无需进行外推。 绝大多数情况下，研究者所真正关心的因素都是固定因素。 例如：

  • 性别：只有两种。
  • 疗法：只有三种。

• 随机因素（Random Factor）：

  • 该因素所有可能的取值在样本中没有都出现，目前在样本中的这些水平是从总体中随机抽样而来，如果我们重复该研究，则可能得到的因素水平会和现在完全不同！
  • 这时，研究者显然希望得到的是一个能够“泛化”，即对所有可能出现的水平均适用的结果。这不可避免的存在误差，需要估计误差的大小，因此被称为随机因素。

5.2.2 单因素方差检验

• 检测3组以上人群在某个连续变量均值上是否存在差异，或者某个分类变量对某个连续变量是否存在显著相关。

• 用到的变量：因变量是一个且为连续变量；自变量是一个分类变量

• 原假设：自变量与因变量之间不存在显著相关（不同人群之间在该连续变量的均值上没有显著差异）。

• 分析结果：

  1. 两两比较中根据方差齐性检验结果，来选择方差相等的比较结果或方差不等的检验结果。
  2. 当方差不齐时，则通过非参数检验中的K个独立样本检验法进行检验。

5.2.3 多因素方差检验

• 检测多个连续变量在某个连续变量均值上是否存在差异，或者多个变量对某个连续变量是否存在显著相关。

• 用到的变量：因变量是一个且为连续变量；自变量是多个分类变量或连续变量。

• 原假设：多个自变量与因变量之间不存在显著相关。

• 分析模型：

  • 全因子模型：既考虑所有自变量对于因变量直接效应，又考虑所有分类变量的交互作用对因变量的影响。

  • 定制模型：可根据研究者自身需求，定制需要考虑的对因变量的影响因素。比如只考虑自变量的直接效应，或部分自变量的交互作用。

  • 当自变量特别多时，尤其是分类自变量特别多时，且样本量不多时，应该使用定制模型，否则可能导致某些单元格里没有元素。

5.2.4 重复方差检验

• 指一个因变量，在多个时刻重复测量多次，自变量可以有也可以没有

• 可以看做配对样本T检验，应用场景一样

第二部分 多指标统计

1 多变量分析方法的选择

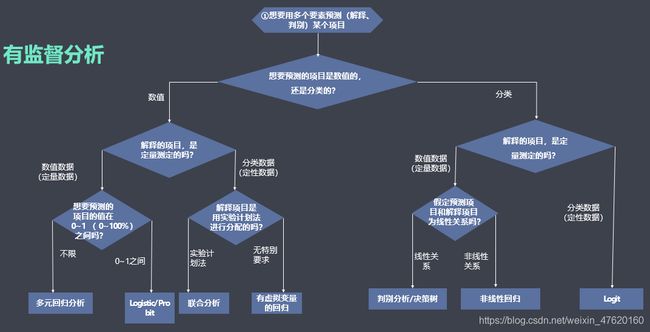
1.1 有监督分析

• 数据中有因变量，则建立有监督模型：
  1. 因变量为连续变量（建立的模型又称为回归预测模型）：
     1. 当自变量全部为连续变量时，可选择回归分析、方差分析。
     2. 当自变量为分类变量（或分类+连续变量）时，可选择带虚拟变量的回归分析、联合分析、方差分析。
  2. 因变量为分类变量（建立的模型又称为分类预测模型）：
     1. 当自变量为连续变量（或分类+连续变量）时，可选择判别分析、Logistic、probit回归等。
     2. 当自变量全部为分类变量时，可选择对数线性回归。
• 有监督模型具有两大通用目的：
  • 分析哪些自变量对因变量存在显著影响作用。
  • 通过选择对因变量存在显著影响的自变量，建立预测因变量取值的预测模型。
• 总结：

1.2 无监督分析

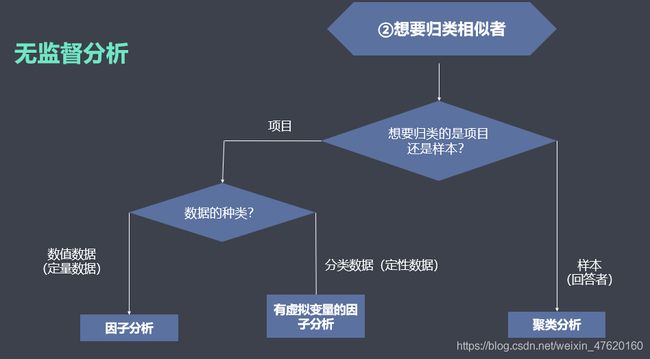
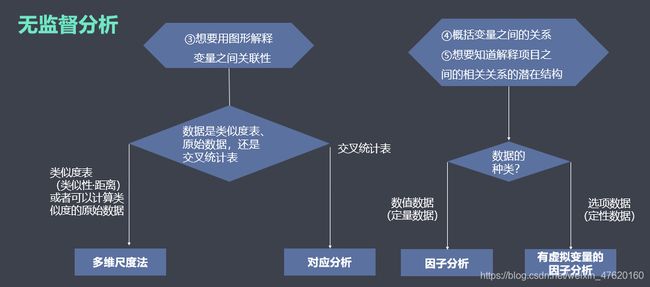
• 数据中无因变量，则建立无监督模型：

  1. 自变量为连续变量时，可选择因子分析（对变量/指标分类）、聚类分析（对人或者对变量/指标进行分类（很少人知道））
  2. 自变量为分类变量时，可选择对应分析（对人分类）、多维尺度分析（对人分类）

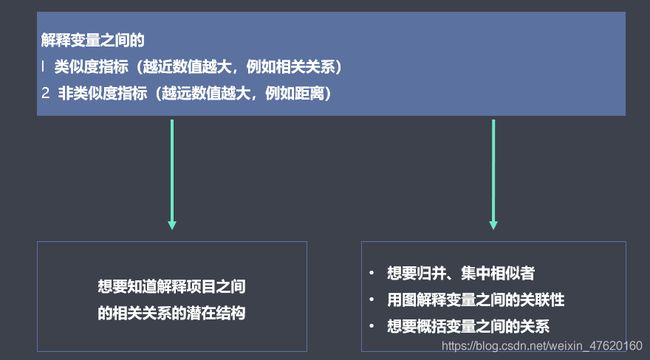
• 无监督模型的目的：

  1. 对人进行分类。
  2. 对变量/指标进行分类。
  3. 分析变量与变量之间的测量关系。

• 无监督的规则：

• 总结：

1.3 其他分析

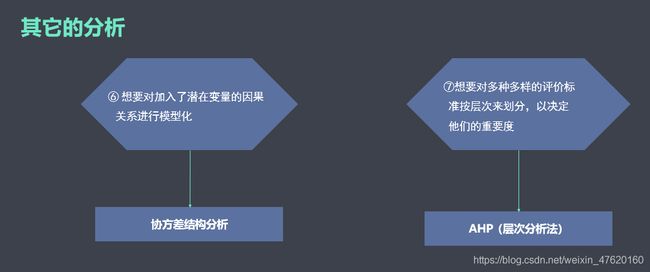
• 当模型中需要加入潜变量（通过多个客观指标(显变量)测量的抽象概念）或需要考虑多个变量之间的因果关系时，可选择结构方程模型、路径模型、协方差分析等。

• 综合评价：通过多个指标对多个评价对象进行排名，可选择层次分析法、因子分析等。

• 总结：

1.4 小结

2 相关性分析

2.1 相关分析

• 相关分析：职业种类和收入之间的关系、政府投入和经济增长之间的关系、广告投入和经济效益之间的关系、治疗手段和治愈率之间的关系等等。这些都是二元的相关分析。

  还有更加复杂的诸多变量之间的相互关系：比如企业的固定资产、流动资产、预算分配、管理模式、生产率、债务和利润等诸因素的关系是不能用简单的一些二元关系所描述的。

• 相关分析常用方法：

  • 散点图
  • 计算相关系数

• 相关分析场景：

  1. 二元相关分析：当时只有两个变量时使用，分析方法是计算相关系数，如下文所说的3个重要相关系数，是最常用的分析方法。
  2. 偏相关系数（要控制住其他相关变量）：在很多现实情况，单纯两个变量之间的相关性，还会受到其他变量的干扰，因此考察两个变量的相关性时往往需要剔除干扰变量的影响，再来计算相关性。比如，商品需求量和价格、消费者收入之间的关系，需求量与价格之间的相关关系还包含了消费者收入对商品需求量的影响。同时收入对价格也会产生影响，并通过价格变动传递到对商品需求量的影响中。
  3. 典型相关分析（比较少用，有更好的方法）：又称为规则相关分析，用来分析两组变量整体的相关性，而不是变量个体之间的相关性，两组变量的个数可以不同。测量的仍然是变量之间的线性相关性。要求每组内的变量也呈现线性关系，另外组内变量间不能存在高度的复共线性。原始数据标准化之后再计算，则得到标准化的相关系数。
  4. 距离分析（应用比较少，其他分析方法里有相应的方法）：当数据包含多个变量，将这些变量按照一定的标准（距离）分类，进行聚类分析。

2.2 相关系数

• 相关系数：相关系数能用来衡量两个变量之间变化趋势的相似性。 它表示在2个变量之间，其中一个增加，另一个也随之直线增加或者减少的关系的指标。 相关系数表示线性关系，不表示曲线关系。在统计中，相关系数用 r 这个符号来表示。

• 不同变量类型的相关系数：

  • 两个变量都为连续变量，则可用pearson相关系数。
  • 两个变量都为定序变量，则可用GMMA等相关系数。
  • 两个变量都为定类变量，则可用LAMMDA等相关系数。
  • 一个变量为定类变量，一个变量为连续变量，则可用ETA系数。

• 三个重要相关系数：

  • pearson相关系数：属于参数检验方法，需要两个参数服从双变量正态分布（与两个变量均服从正态分布有差别），针对两个都是连续变量的数据进行相关性判断。

    相关系数	相关性
    0 - 0.2	较弱相关
    0.2 - 0.4	弱相关
    0.4 - 0.6	一般
    0.6 - 0.8	较强相关
    0.8 - 1	极强相关

  • spearman等级相关系数：用来测量两个定序变量的相关系数。小样本时，spearman等级相关系数服从spearman分布；大样本时近似服从正态分布。属于非参数统计方法，对变量的分布没有要求。

  • Kendall’s tau-b等级相关系数：同样是测量两个定序变量的相关系数。小样本时，该相关系数服从kendall分布；大样本时近似服从正态分布。属于非参数统计方法，对变量的分布没有要求。

• 两个参数之间有相关性，不一定背后就存在因果关系，也有可能是伪相关，例如太阳落下和月亮升起。

  伪相关，又称伪关系、虚假关系，顾名思义是虚假的“关系”，但此处的关系指的是因果，而非相关，即两因素间本不存在因果关系，却被误认为存在。这种错误出现的原因包括忽略了第三方潜在因素的影响，如前文介绍伪相关的例子，地球自转对太阳落山与月亮上山的影响。严格意义上说，因为伪关系描述的是因果，如两事物间的本身不被认为有因果关系，那也不会是伪关系。根据一些学者的说法，伪关系是相关向因果迈进的必经阶段，排除了伪关系因素的相关研究才可能进一步探索因果关系。
  对于伪关系的剔除目前主要有两种方法：实验与纯统计检验。前者通过尽可能控制其它潜在影响因素，操纵其中某一变量并观测另一变量的变化来明确两者间的关系；后者则更多应用于一些无法付诸实验而采用观测数据的学科，如经济学。

2.3 相关分析的假设检验

原假设：两个变量来自的总体中没有显著相关性。

研究假设：两个变量来自的总体中有显著相关性。

显著性检验的目的：是用来判断两个变量在总体中是否存在相关性。

相关系数的目的：是计算两个变量在样本数据中的相关性强弱。

TIPS：偏相关分析计算相关性的变量为连续变量时，加入控制的变量必须也是连续变量

3 回归分析

上面所学的内容都属于假设检验，是为建模分析做的探索性分析方法，属于基础分析方法。从这章开始，我们真正地进入多变量建模分析方法，接下来的方法都要遵循一定的建模过程。

3.1 回归分析简介

• 当需要用一个数学表达式（模型）表达多个因素（原因）与另外一个因素（因素）之间的关系时，可选用回归分析法。

• R²是皮尔森相关系数r的平方，用来衡量自变量对因变量的解释能力，即模型的解释能力。R²的取值为0-1之间。R²的值越接近1，说明回归直线对观测值的拟合程度越好；反之，R²的值越小，说明回归直线对观测值的拟合程度越差。

• 回归分析模型的应用：

  • 分析哪些自变量对因变量存在显著影响作用，模型的R²值可以不要求大于0.8。
  • 通过选择对因变量存在显著影响的自变量，建立预测因变量取值的预测模型，模型的R²值必须大于0.8。
  • 在人文社科领域，很多回归模型的R²值达不到0.8，也可以用来做预测；在金融领域，要求R²值大于0.9才能用来做预测。
  • 在某些特殊领域（如地震预测），即使R²值大于0.99也无法来做预测。

3.2 回归分析分类

• 回归分析模型：探察变量之间的数量变化规律，并通过一定的数学表达式（即模型）来描述这种关系，进而确定一个或几个变量（即自变量）的变化对另一个变量（即因变量）的影响程度 。

• 回归分析是研究变量间统计关系的方法，回归分析模型的类型如下：

  • 因变量与自变量都是连续变量的回归分析 ：普通回归分析 。
  • 因变量是连续变量，自变量中有分类变量的回归分析 ：含有哑变量（虚拟变量）的回归分析。
  • 因变量是分类变量的回归分析：Logistic回归分析 。

• 回归分析的分类

  • 根据自变量个数：
    • 一元回归
    • 多元回归
  • 根据因变量类型：
    • 连续变量的回归（回归模型）
    • 分类变量的回归（分类预测模型、分类回归）
  • 根据自变量与因变量的关系：
    • 线性回归
    • 非线性回归

3.3 回归分析前提

• 线性趋势： 自变量和因变量的关系是线性的，如果不是，则不能采用线性回归分析。是否线性可以通过散点图来加以判断。

• 独立性： 因变量的取值相互独立，之间没有联系。反映到模型中要求残差间相互独立，不存在自相关，否则应采用自回归模型分析。

• 正态性： 自变量的任何一个线性组合，因变量均服从正态分布。反映到模型中要求残差服从正态分布

• 方差齐性： 就自变量的任何一个线性组合，因变量的方差均相同。反映到模型中要求残差的方差齐性。

3.4 回归分析过程

• 回归的步骤

  1. 确定变量：

     • 自变量：前人的研究成果、个人经验、站在前人的基础上结合个人经验进行创新
     • 因变量：根据研究需求或问题推导出来

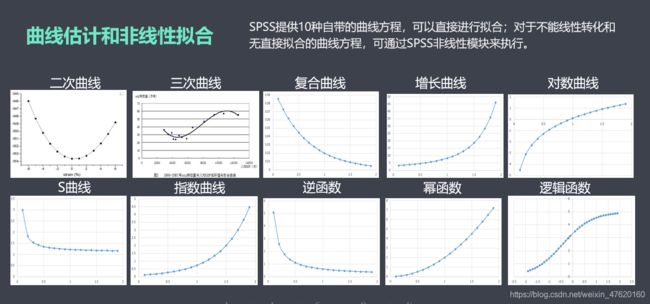
  2. 确定自变量与因变量之间的关系：

     • 线性关系
     • 非线性关系（二次、三次、指数、对数、S型、增长曲线等）

     首先，逐一将自变量与因变量画散点图，判断每个自变量与因变量之间是线性还是非线性关系。

     其次，通过卡方检验、T检验、F检验或相关分析法，逐一分析每个备选的自变量与因变量之间是否存在显著的相关性，将与因变量明显没有相关性的自变量剔除掉，不加入到后期模型中。

     TIPS：筛选自变量的方法：

     • 向前筛选法：是自变量不断进入回归模型的过程。首先，选择与因变量具有最高线性相关系数的自变量进入模型，并进行回归分析的各种检验；然后，在剩余的变量中寻找与自变量偏相关系数最大且通过检验的变量进入模型，并对新建立的模型进行各种检验；这一过程一直重复，直到再也没有可进入模型的变量为止。

     • 向后筛选法：是自变量不断剔除出回归模型的过程。首先，所有变量全部选入回归模型中，并对回归方程进行各种检验；然后，在回归系数显著性检验不显著的一个或多个变量中，剔除t检验值（或其他检验值）最小的变量，并重新建立回归方程并进行各种检验；如果新建回归模型中所有变量的回归系数检验都显著，则回归方程建立结束。否则按照上述方法再依次剔除最不显著的变量，直到再也没有可剔除的变量为止。

     • 逐步筛选法：是向前筛选和向后筛选的综合。随着变量的不断引入，自变量之间可能存在一定程度的多重共线性，使得某些已经进入模型的自变量不再显著，这样造成最终回归模型可能包含一些不显著的自变量。逐步回归是在向前筛选基础上，结合向后筛选，在每个变量进入模型后再次判断是否存在应该剔除的自变量。

  3. 建立回归方程：

     • 线性回归方程
     • 非线性回归方程（二次、三次、指数、对数、S型、增长曲线等）

  4. 回归方程计算与检验，对模型进行全方位检验：

     自变量与因变量关系的检验：

     • 通过散点图大致判断是线性还是非线性关系（已在第二步完成）。

     自变量之间关系的检验：

     • 多重共线性检验（相关分析法、VIF/容忍度）：检验多个自变量之间是否存在相关性较高的变量，如有，则保留与因变量相关性最高一个自变量。

     模型拟合优度检验：

     • 方差检验：检验自变量与因变量是否存在显著影响关系。
     • 判定系数（R方）：0-1之间，越接近1表示自变量对因变量的解释能力越高，模型越好。
     • 残差检验：常用的方法包括残差正态性检验、DW检验、异方差检验。残差存在自相关性表示残差里还存在一些信息未被发现。
     • 自变量参数检验（参数估计方法：普通最小二乘法和极大似然估计）。

     参数显著性检验：

     • 通过T检验或其他非参数检验方法，检验每个自变量是否对因变量存在显著影响关系（已在第二步完成）。

  5. 预测： 通过已知的自变量取值，利用回归方程预测未知的因变量。

3.5 虚拟变量（哑变量）

原因：分类变量无法参与到回归模型中的加减乘除运算。

操作：将原先的分类变量编码统一转换为0、1数值。

• 如果回归模型有截距项，有m种互斥的属性类型，在模型中引入（m-1）个虚拟变量。
• 如果回归模型无截距项，有m个特征，设置m个虚拟变量。

3.6 回归分析SPSS案例

• 解决问题：分析影响人们家庭收入的因素有哪些，建立预测收入的回归方程。（数据源：SPSS自带数据telco.sav）

• 因变量：家庭收入

• 自变量：年龄、工作年限、性别、学历

• SPSS操作： 分析-回归-线性（先全部输入，再用逐步筛选法）

  • 统计：选入共线性诊断、残差DW检验
  • 画图：残差直方图和正态图

• SPSS回归分析结果解读：

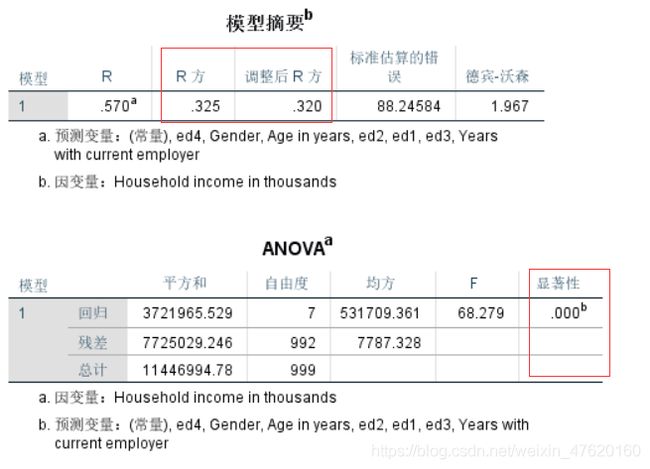
  1. 拟合优度检验：

     由R方值和方差检验构成，如F值对应的概率P值小于0.05，则研究假设成立，即至少有一个自变量对因变量存在显著影响。

     

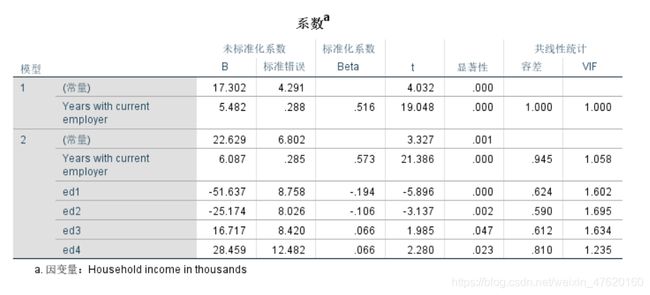
  2. 参数显著性检验：

     根据每个自变量的T值对应的概率P值是否小于0.05，如小于0.05，则研究假设成立，即该自变量对因变量存在显著影响。

     
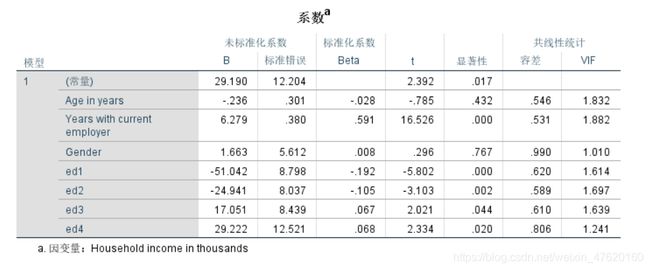
     根据上表得出，工作年限和学历对收入有显著影响，而年龄和性别则没有显著影响。

     通过标准化系数来判断两者对收入影响程度的程度，可知工作年限的影响明显大于学历。

     通过非标准化系数可知：

     1. 在其他变量不变的情况下，工作年限每增加一个单位（年），则家庭收入平均增加6.279个单位。
     2. ed1=-51.042，表示ed1代表的学历（高中以下）人群比对照组的学历（大专）人群在家庭收入上，平均低51.042个单位。

  3. 共线性检验： 若VIF>10，则表示自变量之间存在共线性，容差和VIF值之间是倒数关系。

  4. 残差检验： DW值约等于2，表示残差不存在自相关性。

  5. 回归方程： 先通过逐步回归法，将对因变量没有显著影响的自变量从模型中删除（ed1-4要放到下一层，否则部分会被筛选出去），得到干净的模型。

     方程：y=22.629+6.087*工作年限-51.637*ed1-25.174*ed2+16.717*ed3+28.459*ed4*

     

3.7 非线性回归

• 非线性回归的两种求解方式：

  1. 做线性转化，原因是非线性方程拟合方法和参数初始值设置均会导致求出的结果并非全局最优解，因此非线性回归方程尽量做线性转化。

     

     

  2. 直接建立非线性方程，求解非线性模型。

     

• 非线性回归计算时注意的几个问题：

1. 参数初始值设置：
   • 多选几个初始值进行拟合，观察最终分析结果是否相同。如果相同自然皆大欢喜，如果不同，则比较这几个解何者最优（比较R²值）；
   • 当模型表达式可解时，先从图形上取几个点，解出各参数的近似值，然后作为初始值代入。这些近似值往往与实际值非常接近，从而避免了局部最优解的问题；
   • 如果模型过于复杂，则最好在迭代时首先简化模型，拟合不太复杂的雏形。然后逐步添加内容，最终拟合目标模型。
2. 拟合方法的选择：
   • SPSS提供两种拟合方法：Sequential Quadratic Programming和Levenberg - Marquardt。前者为默认方法，适合较简单的模型。当使用特殊的损失函数时，或对参数取值范围进行设定时，该方法将不可用，将选用后者方法。
   • 对于较复杂模型，大样本的数据时，可考虑使用Bootstrap抽样统计的推断方法，计算时间会延长较多。

3.8 回归分析总结

• 回归方程具有特定的形式。例如，因变量表示为截距、自变量的线性组合，及残差的和。不满足这一假设，可能原因：
  • 忽略了重要的自变量
  • 包含了不相关的自变量
  • 非线性－因变量和自变量之间的关系是非线性的
  • 变动的参数－数据收集期间，方程中参数不是常数（即y=ax+b中的a不是固定的常数，收集数据的时候有可能随着时间变动）
  • 非可加性－自变量中某个给定变量的影响是附随着其它变量的（即变量之间也有相关关系）

4 因子分析/主成分分析

4.1 目的和应用场景

• 因子分析直接应用目的：对多个具有较高相似性的变量/指标进行降维， 前提是这些变量/指标直接必须存在一定的相关性/相似性。
• 应用场景：
  • 降维后做综合评价： 想要知道品牌印象的构造（想通过少数的潜在因子来解释印象）；或者想要归纳出消费者的若干种态度；亦或不测量综合满意度，但想通过个别满意度来计算出综合满意度指数。
  • 效度检验： 对抽象概念的测量工具进行有效性检验，判断哪些指标需要保留或者删除，并对保留的指标进行维度划分。
  • 降维后做其他分析： 由于变量存在较高相关性，不适合做回归、聚类等其他分析，需要用因子分析消除变量间较高的共线性。

4.2 因子分析前提

• 样本量大小： 样本量（行）与变量数（列）的比例应在5：1以上，且总样本量不得少于100，而且原则上越大越好。

  TIPS：如果软件提示数据不正定，则代表样本量不够（应增加样本量或者减少变量数量）。

• 各变量间必须有相关性：

  • 一般以KMO统计量判断相关性：0.9最佳，0.7尚可，0.6较差，0.5以下放弃(一般以0.7为标准，要求大于0.7，小于0.7一般认为不适合做因子分析) 。
  • 还可以用Bartlett球形检验： 若相关矩阵为单位矩阵（P值大于0.05），则因子分析无效。

4.3 因子分析程序

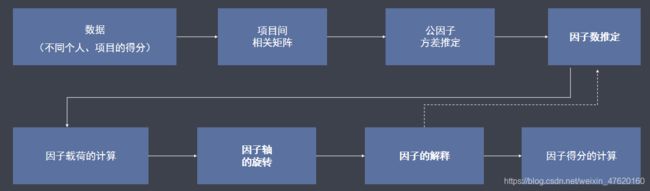
因子分析的程序：从相关矩阵出发，在公因子方差推定和因子数推定的基础上，计算因子载荷，然后旋转因子轴，计算因子得分。

4.3.1 什么是因子

所谓因子，是指造成某种现象的原因和先行条件。因子分析是心理学家为了把握人的心理能力而开发出来的。原来是为了解释多种学力测试的相关关系而着力开发出来的方法。

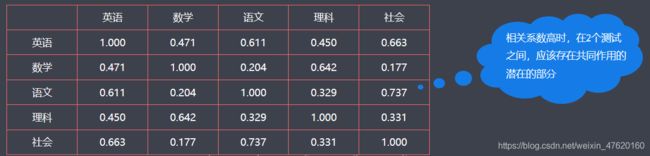
在心理学中，通过测试相互间的相关关系数表（相关行列）思考如下的问题：英语的得分和社会的得分相关性最高，数学和理科、语文和社会的相关性最大。因此，把它们存在共同作用的潜在部分称为因子（factor）。

持有某种因子多的人（即潜在变量的值，也称为因子得分），两科的测试都取得高分；相反，持有某种因子少的人，两方的测试都取得低分。因此，测试的相关性是可以解释的。

相关矩阵：

4.3.2 因子数推定

在公因子方差的推定结果的基础上，用把相关矩阵的对角元素置换成公因子方差的矩阵，来进行因子数的推定。

为了推定因子数要进行主成分分析，求特征值。特征值是表示变量的信息量大小的指标。特征值越大，可以说就是越重要的元素。

主成分分析与因子分析一样，它分析相关关系，以尽可能少的变量的变动来说明所有数据所拥有的信息量（方差）。

推定因子数的方法主要有3种：

• 建立在特征值的数值基础上的方法： 以特征值1.0以上的数作为因子数。
• 建立在碎石图基础上的方法： 将特征值按从最大值到最小值的顺序排列，看其减少的情况。从某个阶段开始，特征值突然变小之后，可以考虑把稳定阶段作为因子数，在这以下则为误差因子（很少使用这种方法）。
• 建立在累积特征值的百分比的基础上的方法： 计算特征值的累积百分比，把累积百分比变成60%~80%的数作为因子数。

4.3.3 因子轴旋转

在计算出来的因子载荷的基础上对因子进行解释，寻找意识结构，才是因子分析的最高境界。但是，对计算出来的因子载荷，原封不动地进行解释是有困难的。

变量的因子载荷为1或者0时，因子的解释比较简单。例如，第1因子，由于变量a• b• c三者相关，其他变量不相关，就要对让abc三者产生印象的情况进行解释。我们把这样的想法称为“单纯形”。为了得到单纯形，应该把因子载荷矩阵的数字变成1或者0，让因子轴旋转。

旋转方法有多种，常用的有：

• 正交旋转：
  • 方差最大正交旋转（最普及的方法）
  • 一般正交旋转（一般的方法）
• 斜交旋转：
  • promax旋转（追求因子的单纯形的方法）
  • oblimin旋转（使不同因子之间的协方差最小的方法）

旋转后的因子载荷，正交旋转在+1到-1之间取值，斜交旋转有时会超出±1的数值范围。

因子旋转的目的：

1. 使得因子可以更好的代表原来的变量；
2. 降低或消除提取因子之间的相关性。

4.3.4 因子的解释

• 因子解释是根据旋转后的因子载荷矩阵（斜交旋转时的因子模型矩阵）的数字来进行探讨。
  适用单纯结构的想法，因子载荷的绝对值在0.4以下时可以忽略。把因子载荷看作因子和项目（变量）的相关关系。因子载荷的绝对值越大，其与它的因子的关系就越强。 每个因子，如果按照因子载荷绝对值大小的顺序，变更排列项目（变量），对解释会更加方便。

• 因子的命名： 一种是简称，还有一种是详细的名字。如果简称可以很好地命名，详细的名字就不需要了。
  在调查报告会上，在对因子分析进行说明时，分析能否得到理解的关键是命名。站在报告接受者的立场，请用容易理解的语言，做一个给因子起名的人。

4.3.5 因子得分计算

因子得分，通过如下因子分析模型来求得：
$$F=Z{R}^{-1}A$$
F：因子得分矩阵（n人×m因子，已经进行标准化）

Z：变量的标准化得分矩阵（n人×p个变量）

R^-1：相关矩阵的逆矩阵

A：旋转后的因子载荷矩阵

求出来的因子得分，以平均数0，标准差1进行标准化处理。利用因子得分，可以考虑进行以下的分析：

• 按组来划分的因子得分平均值的比较: 与交叉统计一样，如果在按性别、年龄等来划分的交叉主项目下对因子得分进行比较，组的特征就会变得明确起来。如果进行方差分析，组间的差异则在统计学意义上得到明确。
• 按因子得分的顺位来划分的交叉统计: 把因子得分划分为排行居前25%，居后25%，居中50%，即使进行前25%、后25%的分析，或许也可以得出令人感兴趣的结果。
• 新的多变量分析数据 : 用因子得分，可以进行聚类分析。由于数据的精华达到了因子得分这样的极致，因此，其他的多变量分析也可以充分地使用。

4.3.6 效度检验

• 效度检验是否通过判断标准：
  1. 每个变量有且只有一个因子载荷值大于0.5，如果所有因子载荷值均小于0.5，则说明该变量不具有收敛效度（相似性不够，不能跟其他变量放在一类，收敛度不够，需要删除）。
  2. 变量在两个或以上因子中的载荷值同时大于0.5，则说明该变量不具有区分效度，需删除。
  3. 变量单独成为一个因子，则说明该变量也不存在收敛效度，需删除。

4.4 因子分析的SPSS案例

• SPSS操作： 分析-降维-因子

  • 描述：KMO检验
  • 提取：碎石图
  • 旋转：最大方差法、载荷图
  • 得分：保存为变量、显示因子得分系数矩阵
  • 选项：按大小排序、排除小系数、绝对值0.3

• 结果解读：

1. KMO和巴特利特检验：KMO>0.7，适合做因子分析；P值<0.05，适合。

2. 公因子方差：初始栏中的数据代表原始变量包含的信息（为1，代表100%），提取栏中的数据代表因子从中提取了X%的信息量。

3. 总方差解释：提取特征值大于1的因子数；方差百分比代表每个因子提取的信息量；累积方差贡献率代表加一起总共提取了多少信息量（效度检验和降维后做其他分析，起码要提取60%以上的信息量才有代表性，效度检验甚至可以不看累积方差贡献率；如果通过因子分析降维后做综合评价，那么累积方差贡献率要大于80%）。

4. 成分矩阵：没有进行旋转的初始提取因子的因子载荷值分布图。

5. 旋转后的成分矩阵：按因子载荷值（绝对值）>0.5选择每个变量所对应的因子。

6. 旋转后的载荷图：一般不看。

7. 成分得分系数矩阵：用来做因子得分计算，公式如下。
   $$F_n=X_1\times A_1+X_2\times A_2+\cdots +X_n\times A_n$$

   • F： 各因子得分 X： 矩阵内系数 A： 各变量的取值

5 逻辑回归（Logistic）

5.1 应用场景及理论

• 应用场景： 分类预测模型，且为非参数检验方法，可以用于二分类、无序多分类、有序多分类。

• 理论背景：

  例如，看不看广告，或者购买不购买商品的概率，会因性别、年龄和职业的不同而有所变化。

  在这里，将看广告（或者购买）的概率[P]和不看广告（或者非购买）的概率 [1-P]的比，称作奇数比（OR值）。

  奇数比，如果用赌输赢来比喻，就是胜的概率与负的概率的比。在医学上则变成了治愈率与死亡率的比。

  因变量取值为0、1，P为因变量取值为1的概率。

  因变量的组分为2组时，称作二项逻辑斯谛回归分析。3组以上时，则称为多项逻辑斯谛回归分析。

5.2 二元逻辑回归的SPSS案例

• SPSS操作： 分析 - 回归 - 二元logistic

  • 分类：将分类变量选入分类协变量中
  • 保存：概率、组成员（最终预测类别）
  • 选项：置信区间95%

• 结果解读：

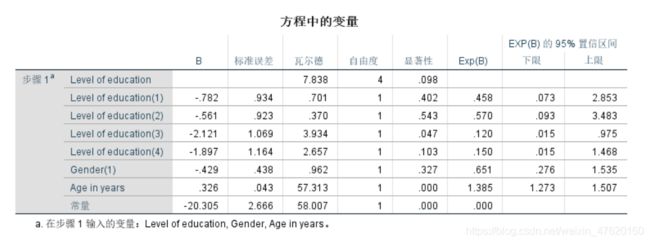
  1. 根据参数检验中（下图）的P<0.05，得到自变量对因变量存在显著影响；

  2. 根据wald值，判断自变量对因变量的影响程度排名，wald值越大对因变量的影响程度越高；

  3. 优势比B值（OR值）大于1，表示该自变量会增加因变量取1的情形的发生概率，反之会降低概率；

  4. 连续自变量对因变量的影响程度：在其他变量不变的情况下，当年龄增加一个单位（岁）时，优势比增加1.385倍（年龄越大，退休概率越大）；

  5. 分类自变量对因变量的影响程度：在其他变量不变的情况下，大专学历的优势比是研究生学历优势比的0.120倍（大专学历的退休概率低于研究生学历的退休概率）；

  6. 二元逻辑回归方程：
     $$ln(\frac{p}{1-p})=-20.305-0.782ed1-0.561ed2-2.121ed3-1.897ed4-0.429Gender+0.326Age$$

5.3 有序多元逻辑回归的SPSS案例

• SPSS操作： 分析 - 回归 - 有序

  • 输出：平行线检验、估算响应概率、预测类别、预测类别概率

• 结果解读：

  1. 拟合优度检验：判断期望频数与观察频数是否有显著差异，P值越大越好；

  2. 平行线检验：概率P值大于0.05才能进行有序逻辑回归分析，否则改用无序回归分析模型；

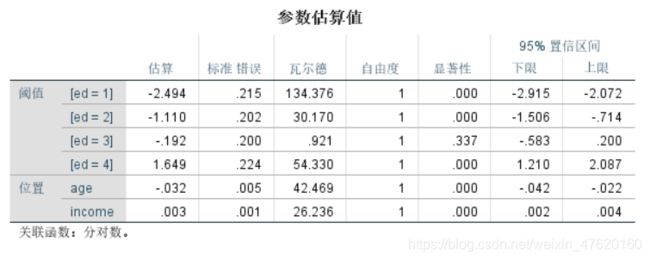
  3. 有序多元逻辑回归方程：

     1. p1表示学历取1的概率：
        $$ln(\frac{p}{1-p})=-2.494-0.032Age+0.003income$$

     2. p1表示学历取1、2的概率：
        $$ln(\frac{p}{1-p})=-1.110-0.032Age+0.003income$$

     3. p1表示学历取1、2、3的概率：
        $$ln(\frac{p}{1-p})=-0.192-0.032Age+0.003income$$

     4. p1表示学历取1、2、3、4的概率：
        $$ln(\frac{p}{1-p})=1.649-0.032Age+0.003income$$

6 时间序列分析

6.1 时间序列背景及特点

时间序列分析： 按照时间的顺序把随机事件变化发展的过程记录下来就构成了一个时间序列。对时间序 列进行观察、研究，找寻它变化发展的规律，预测它将来的走势就是时间序列分析。

• 从统计意义上说，时间序列是一个统计指标在不同时刻上的数值，按照时间顺序排成的数列 ，由于统计指标数值受到各种偶然因素影响，因此这数列表现出随机性。
• 从系统论上说，时间序列是某一系统在不同时刻的响应，是系统运行的历史行为的客观记录 。
• 时间序列的特点:
  • 序列中的数据依赖于时间顺序
  • 序列中每个数据的取值具有一定的随机性
  • 序列中前后的数值有一定的相关性——系统的动态规律
  • 序列整体上呈现某种趋势性或周期性

6.2 时间序列分析方法

• 纯时间序列方法：
  • 移动平均（Moving Average）：用最近的几项数据的均值进行预测
  • 简单指数平滑法（Exponential Smoothing）：用最近几项数据的加权均值进行预测
  • 趋势调整的指数平滑法（Holt、Brown）：在简单指数平滑上增加了趋势估算
  • 趋势季节调整的指数平滑法（Winter 乘法、加法）：在简单指数平滑上增加了趋势估算以及季节因子
  • 简单ARIMA
• 因果时间序列方法：
  • Multivariate ARIMA：带有因果关系的时间序列分析方法
    • 格兰杰因果检验：因果关系成立的三个条件
      1. A、B两个事件必须存在相关性
      2. 原因A必须发生在结果B之前
      3. 排除其他干扰因素（没有A或者A+C会不会导致B的发生）

6.3 时间序列分析要求

• 历史数据越多，对预测帮助越大：样本点越多，时间序列的过去规律就越清楚。不要希望通过收集到的两个月的销售数据来预测未来两年的销售额。因为你的样本量为2，只有一个季节周期的六分之一，却要求预测未来24个月，或者未来两个完整的季节周期（一般要求有15个样本量才能预测1个未来的同周期数据）。

• 数据量最低限制 取决于多方面因素，但没有明确数量要求 ：

  • 周期性： 一般情况是如果建立季节模型，4个或者以上季节周期的数据
  • 数据采集频率
  • 模型复杂程度： 模型越复杂，样本点越多越好

6.4 时间序列数据的预测方法

• 神经网络
• 回归树： 可理解为分段回归。
• 线性回归：
  • 以时间为自变量；
  • 以自己过去时间的数值为自变量，也叫自回归模型（Autoregressive model，简称AR模型）。

两种类型的时间序列：

• 平稳序列：是指时间序列的所有统计性质都不会随着时间的推移而发生变化。

  • 均数和方差不随时间变化；
  • 自相关系数（T时刻的数值与T-1时刻的数值计算皮尔逊相关系数）只与时间间隔有关，与所处的时间无关。

• 非平稳序列：ARIMA模型建立的前提是时间序列必须为平稳序列，可通过单位根检验（ADF）来判断一个序列是否平稳。

• 时间序列假设检验：模型是否能通过Ljung-Box Q检验，此检验的原假设是模型与原始数据没有显著性差异，P>0.05表示模型可以接受。

6.5 ARIMA模型

ARIMA：差分整合移动平均自回归模型

• AR：Autoregressive，向量自回归
• I：差分
• MA：Moving Average，移动平均

ARIMA适用场景：

• 该模型只适用于连续性的数据变量预测；
• 即适用于平稳序列也适用于非平稳序列；
• 模型通常包含以下因素：
  • 长期趋势：随时间变化而呈现出的规律现象
  • 季节性（Seasonality）：会根据固定周期呈现周期性的循环变化
  • 周期变动
  • 不规则变动

时间序列中的趋势处理方法： 可通过差分的方式来消除序列数据中的趋势，以建构出平稳的序列 。

时间序列中的季节性处理方法：

1. 非平稳序列剔除趋势后，接下来需要判断是否存在季节性；
   • 消除趋势后的平稳序列，如果存在季节性，会呈现出单纯的季节变化；
   • 季节性（周期性）变化意指数据以固定周期n呈现周期性变化，从数据上来看即为：时间t的数据与时间t-n的数据存在高度的相关性；
   • 通常可通过自相关系数ACF（Autocorrelation Factor）来决定循环周期数，该系数是通过pearson相关系数来描述某个值与前几期值的相关程度；
   • 可通过自相关系数（ACF）图的拐点，乘于4得到变化周期频率；
   • 或者通过频谱图来查看周期频率，用频率最高的点对应的频率乘于数据量得到周期。
2. 通过自相关系数判断数据中的季节性周期后，我们可以利用平滑法（Smoothing）的方式来移除季节性。其中，最简单的方式就是使用移动平均(Moving Average)。

ARIMA模型三个重要参数：

• 参数P： 自回归（AR）模型要用过去多少个时间段
• 参数I： 差分（0：不做差分，1：一阶差分，2：二阶差分）
• 参数Q： 移动平均（MA）中要用过去多久的数来计算均值

截尾和拖尾：

• p阶自回归模型 AR（P）：
  • AR（p）模型的偏自相关函数（PACF）在p阶之后应为零，称其具有截尾性；
  • AR（p）模型的自相关函数（ACF）不能在某一步之后为零（截尾），而是按指数衰减（或成正弦波形式)，称其具有拖尾性。
• q阶移动平均模型 MA(q)：
  • MA(q)模型的自相关函数ACF在q阶之后应为零，称其具有截尾性；
  • MA(q)模型的偏自相关函数PACF不能在某一步之后为零（截尾），而是按指数衰减（或成正弦波形式)，称其具有拖尾性。

模型的选择：

• AR模型：自相关系数拖尾，偏自相关系数截尾；
• MA模型：自相关系数截尾，偏自相关函数拖尾；
• ARMA模型：自相关函数和偏自相关函数均拖尾。

专家建模法（Expert Modeler ）： 该方法可以从以下的模型中自动寻找最优的模型，非常适用初学者。

• 指数平滑法（Exponential Smoothing ）：
  • 简单指数平滑法：适用于没有明显趋势性及季节性时；
  • 霍特线性趋势法：适用于具有趋势性但没有明显季节性时；
  • 布朗线性趋势法：适用于具有趋势性但没有明显季节性时；
  • 阻尼趋势法：适用于具有逐渐衰退的趋势性但没有明显季节性时；
  • 简单季节性法：适用于没有趋势性且季节效应是一个常数时；
  • 温特加法法：适用于具有趋势性且季节效应是一个常数时；
  • 温特乘法法：适用于具有趋势性且季节效应随时间越发明显。
• ARIMA：
  • Autoregressive （p）
  • Difference (d)
  • Moving Average (q)