利用plot_surface命令绘制复杂曲面入门详解

一、引言
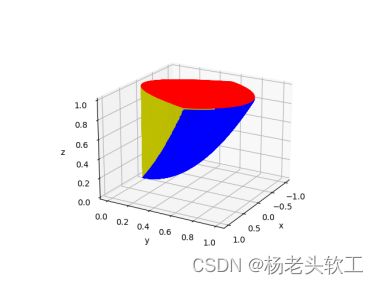
在三维几何图形中，经常需要绘制复杂的曲面，例如封闭的空间曲面。本文以绘制由平面z=1，旋转抛物面z=x^2 + y^2和抛物柱面y=2x围成的封闭曲面为例，详细讲解利用Python命令plot_surface绘制复杂曲面的过程。
二、绘制封闭的曲面
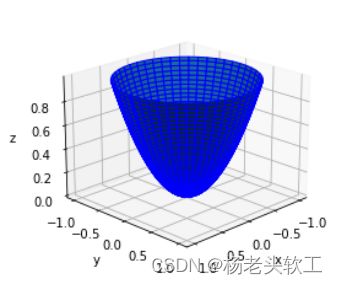
1、首先绘制旋转抛物面z=x^2 + y^2
考虑旋转抛物面函数的定义域是圆域，因此使用极坐标来表示该图形的横坐标和纵坐标，让得到的图形在视觉上更好看一些。
具体的步骤为：
1）首先建立图形窗口，并规定使用三维坐标系
2）确定极径和极角的网格坐标
3）根据直角坐标和极坐标的关系得到旋转抛物面上的横坐标、坐标轴和竖坐标
4）利用plot_surface函数绘制旋转抛物面
5）增加每个坐标轴的标签，确定三维图形的视角
参考代码如下：

import matplotlib.pyplot as plt
import numpy as np
import math

fig = plt.figure()             #建立图形窗口
ax = fig.gca( projection = '3d' )  #使用三维坐标
theta = np.arange( 0, 2 * math.pi, 0.05 )
rou  = np.arange( 0, 1, 0.005 )
T, R = np.meshgrid( theta, rou ) #生成极角和极径的网格坐标
Xp = R * np.cos(T)   #根据极坐标计算横坐标
Yp = R * np.sin(T)    #根据极坐标计算纵坐标
Zp = Xp**2 + Yp**2  #把横坐标和纵坐标代入旋转抛物面函数得到竖坐标
ax.plot_surface( Xp, Yp, Zp, cstride = 1, rstride = 2, edgecolor = 'b' )  #绘制旋转抛物面        
ax.set_xlabel( 'x' )
ax.set_ylabel( 'y' )
ax.set_zlabel( 'z' )
ax.view_init( 20, 45 )

上述代码运行结果为：

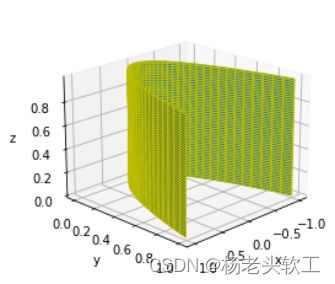
2、绘制抛物柱面y=x^2
有了上面绘制旋转抛物面的经验，此处直接上代码。

fig = plt.figure()   #建立图形窗口
ax = fig.gca( projection = '3d' )  #三维坐标系
Xc, Zc = np.meshgrid( np.arange(-1, 1, 0.005), np.arange(0, 1, 0.005 ) )#自变量网格坐标
Yc = Xc**2
ax.plot_surface( Xc, Yc, Zc, cstride = 1, rstride = 2, edgecolor = 'y' )#绘图
ax.set_xlabel( 'x' )
ax.set_ylabel( 'y' )
ax.set_zlabel( 'z' )
ax.view_init( 20, 45 )

上述代码运行结果为：

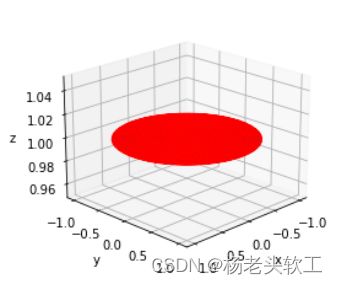
3、绘制与旋转抛物面具有相同定义域的平面z=1
有了上面绘制旋转抛物面的经验，此处直接上代码。

fig = plt.figure()              #建立图形窗口
ax = fig.gca( projection = '3d' )  #三维坐标系
[ m, n ] = np.shape( Xp )
Zf = np.ones( Xp.shape )
ax.plot_surface( Xp, Yp, Zf, cstride = 1, rstride = 2, edgecolor = 'r' ) 
ax.set_xlabel( 'x' )
ax.set_ylabel( 'y' )
ax.set_zlabel( 'z' )
ax.view_init( 20, 45 )

上述代码运行结果为：

4、把上述代码融合到一块运行就可以得到下面的图形：

注意：需要把绘制抛物柱面和平面代码中如下两条语句删除

fig = plt.figure()              #建立图形窗口
ax = fig.gca( projection = '3d' )  #三维坐标系

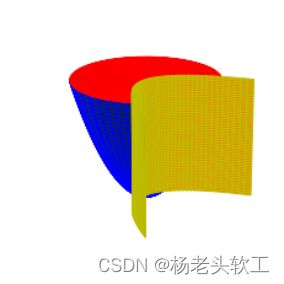
5、删除每个图形上多余的图元
从上图可以看出，结果不尽人意，如果能够去掉各曲面多余的部分，则可以得到比较好看的封闭曲面。因此讲采用下面的代码来分别删除选择抛物面、抛物柱面和平面的多余数据，只需要令多余图元对应的竖坐标分量值为None即可。
1）删除抛物柱面多余的数据（本方法效率比较低）

[ mc, nc ] = np.shape( Xc )
for i in range( mc ):
    for j in range( nc ):
        if Zc[ i, j ] < Xc[ i, j ] * Xc[ i, j ] + Yc[ i, j ] * Yc[ i, j ]:
            Zc[ i, j ] = None
      ```
2）删除选择抛物面和平面多余的数据（本方法效率比较低）
```python
[ m, n ] = np.shape( Xp )
Zf = np.ones( Xp.shape )
for i in range( m ):
    for j in range( n ):
        if Yp[ i, j ] < Xp[ i, j ] * Xp[ i, j ]:
            Zf[ i, j ] = None
            Zp[ i, j ] = None

这样就可以得到如下视觉效果较好的图形：

6、完整的绘制封闭曲面的代码

import matplotlib.pyplot as plt
import numpy as np
import math
#建立图形窗口
fig = plt.figure()
ax = fig.gca( projection = '3d' )#Axes3D( fig )

#旋转抛物面 Paraboloid 的图形数据
theta = np.arange( 0, math.pi, 0.01 )
rou   = np.arange( 0, 1, 0.01 )
T, R = np.meshgrid( theta, rou )
Xp = R * np.cos(T) 
Yp = R * np.sin(T)
Zp = Xp**2 + Yp**2

#抛物柱面 Parabolic Cylinder 的图形数据
Xc, Zc = np.meshgrid( np.arange(-1, 1, 0.01), np.arange(0, 1, 0.01 ) )
Yc = Xc**2
[ mc, nc ] = np.shape( Xc )
#删除抛物柱面多余的数据
for i in range( mc ):
    for j in range( nc ):
        if Zc[ i, j ] < Xc[ i, j ] * Xc[ i, j ] + Yc[ i, j ] * Yc[ i, j ]:
            Zc[ i, j ] = None

#平面 flat surface 的图形数据
Zf = np.ones( Xp.shape )
[ m, n ] = np.shape( Xp )
#删除平面和旋转抛物面多余的数据
for i in range( m ):
    for j in range( n ):
        if Yp[ i, j ] < Xp[ i, j ] * Xp[ i, j ]:
            Zf[ i, j ] = None
            Zp[ i, j ] = None
#绘图
ax.plot_surface( Xc, Yc, Zc, cstride = 1, rstride = 1, edgecolor = 'y' )
ax.plot_surface( Xp, Yp, Zp, cstride = 1, rstride = 1, edgecolor = 'b' )           
ax.plot_surface( Xp, Yp, Zf, cstride = 1, rstride = 1, edgecolor = 'r' )
ax.set_xlabel( 'x' )
ax.set_ylabel( 'y' )
ax.set_zlabel( 'z' )
ax.view_init( 20, 30 )