【时序】Informer:用于长序列预测的高效 Transformer 论文笔记
论文名称:Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting
论文下载:https://arxiv.org/abs/2012.07436
论文年份:AAAI2020
论文被引:173(2022/04/19)
论文代码:
Torch:https://github.com/zhouhaoyi/Informer2020
TF:https://github.com/manjimnav/Informer-Tensorflow
Abstract
Many real-world applications require the prediction of long sequence time-series, such as electricity consumption planning. Long sequence time-series forecasting (LSTF) demands a high prediction capacity of the model, which is the ability to capture precise long-range dependency coupling between output and input efficiently. Recent studies have shown the potential of Transformer to increase the prediction capacity. However, there are several severe issues with Transformer that prevent it from being directly applicable to LSTF, including quadratic time complexity, high memory usage, and inherent limitation of the encoder-decoder architecture. To address these issues, we design an efficient transformer-based model for LSTF, named Informer, with three distinctive characteristics: (i) a ProbSparse self-attention mechanism, which achieves O(L log L) in time complexity and memory usage, and has comparable performance on sequences’ dependency alignment. (ii) the self-attention distilling highlights dominating attention by halving cascading layer input, and efficiently handles extreme long input sequences. (iii) the generative style decoder, while conceptually simple, predicts the long time-series sequences at one forward operation rather than a step-by-step way, which drastically improves the inference speed of long-sequence predictions. Extensive experiments on four large-scale datasets demonstrate that Informer significantly outperforms existing methods and provides a new solution to the LSTF problem.
【时间序列预测的应用】
许多实际应用需要预测长序列时间序列,例如电力消耗计划。
【长序列预测的挑战】
长序列时间序列预测(Long sequence time-series forecasting,LSTF) 需要模型的高预测能力,即能够有效地捕捉输出和输入之间精确的长程依赖耦合(long-range dependency coupling)。最近的研究表明,Transformer 具有提高预测能力的潜力。
【Transformer用于时间序列预测的问题及本文的解决方案】
然而,Transformer 存在几个严重的问题,使其无法直接应用于 LSTF,包括二次时间复杂度、高内存使用率以及编码器-解码器架构的固有限制。为了解决这些问题,我们为 LSTF 设计了一个高效的基于 Transformer 的模型,名为 Informer,具有三个显着特征:
- i)ProbSparse 自注意机制,在时间复杂度和内存使用方面达到 O(L log L),以及在序列的依赖比对上具有相当的性能。
- ii)自注意力提炼通过将级联层输入减半来突出主导注意力,并有效地处理极长的输入序列。
- iii)生成式解码器虽然在概念上很简单,但在一次前向操作而不是逐步的方式预测长序列序列,这极大地提高了长序列预测的推理速度。
在四个大规模数据集上进行的大量实验表明,Informer 显着优于现有方法,并为 LSTF 问题提供了新的解决方案。
1 Introduction
时间序列预测是许多领域的关键要素,例如传感器网络监控、能源和智能电网管理、经济和金融以及疾病传播分析。在这些场景中,我们可以利用大量关于过去行为的时间序列数据来进行长期预测,即长序列时间序列预测(LSTF)。然而,现有的方法大多是在短期问题设置下设计的,例如预测 48 个点或更少。越来越长的序列使模型的预测能力变得紧张,以至于这种趋势正在支撑对 LSTF 的研究。作为一个经验例子,图(1)显示了在真实数据集上的预测结果,其中 LSTM 网络从短期(12 个点,0.5 天)到长期预测变电站的每小时温度周期(480 点,20 天)。当预测长度大于 48 点时(图(1b)中的实心星),整体性能差距很大,其中 MSE 上升到令人不满意的性能,推理速度急剧下降,LSTM 模型开始失败。
LSTF 的主要挑战是提高预测能力以满足日益增长的序列需求,这需要 (a) 非凡的远程比对能力和 (b) 对长序列输入和输出的有效操作。最近,Transformer 模型在捕获远程依赖方面表现出比 RNN 模型更好的性能。自注意力机制可以将网络信号传播路径的最大长度减少到理论上最短的 O(1) 并避免循环结构,从而使 Transformer 显示出解决 LSTF 问题的巨大潜力。然而,自注意机制违反了要求 (b),因为它的 L 二次计算和 L 长度输入/输出的内存消耗。一些大规模的 Transformer 模型在 NLP 任务上倾注了资源并产生了令人印象深刻的结果,但是在数十个 GPU 上的训练和昂贵的部署成本使得这些模型在现实世界的 LSTF 问题上无法承受。自注意力机制和 Transformer 架构的效率成为将它们应用于 LSTF 问题的瓶颈。因此,在本文中,我们试图回答这个问题:我们能否改进 Transformer 模型以提高计算、内存和架构效率,同时保持更高的预测能力?
Vanilla Transformer (Vaswani et al. 2017) 在解决 LSTF 问题时存在三个显着限制:
- self-attention的二次计算。自注意力机制的原子操作,即规范点积 (dot-product),导致每层的时间复杂度和内存使用量为 O ( L 2 ) O(L^2) O(L2)。
- 长输入堆叠层的内存瓶颈。 J 个编码器/解码器层的堆叠使总内存使用量为 O ( J ⋅ L 2 ) O(J·L^2) O(J⋅L2),这限制了模型在接收长序列输入时的可扩展性。
- 预测多头输出的速度骤降。vanilla Transformer 的动态解码使逐步推理与基于 RNN 的模型一样慢(图(1b))。
有一些关于提高自注意力效率的先前工作。来降低 self-attention 的复杂度。
| Model | Method | Complexity |
|---|---|---|
| Sparse Transformer (Child et al. 2019)、LogSparse Transformer (Li et al. 2019)、Longformer (Beltagy, Peters, and Cohan 2020) | 启发式方法来解决限制 1 | O(L log L),但效率增益是有限的 |
| Reformer (Kitaev, Kaiser, and Levskaya 2019) | 局部敏感的哈希自注意力 | O(L log L),但仅适用于极长的序列 |
| Linformer (Wang et al. 2020) | O(L),但对于现实世界的长序列输入,投影矩阵无法固定,这有退化到 O(L2) 的风险 | |
| Transformer-XL (Dai et al. 2019)、Compressive Transformer (Rae et al. 2019) | 使用辅助隐藏状态来捕获远程依赖 | 这可能会放大限制 1,不利于打破效率瓶颈 |
上述工作主要集中在限制 1 上,而限制 2 和 3 在 LSTF 问题中仍未解决。为了提高预测能力,我们解决了所有这些限制,并在提出的 Informer 中实现了超越效率的改进。
为此,我们的工作明确地深入研究了这三个问题。我们研究了自注意力机制中的稀疏性,改进了网络组件,并进行了广泛的实验。本文的贡献总结如下:
- 我们提出的 Informer 成功提高 LSTF 问题的预测能力,这验证了类 Transformer 模型在捕获长序列时间序列输出和输入之间的个体远程依赖关系的潜在价值。
- 我们提出了 ProbSparse 自注意力机制来有效地替代规范自注意力。它在依赖对齐上实现了 O(L log L) 时间复杂度和 O(L log L) 内存使用量。
- 我们提出了自注意蒸馏操作,以优先处理 J-stacking 层中的主要注意分数,并将总空间复杂度大幅降低到O((2 - epsilon)L log L),这有助于接收长序列输入。
- 我们提出生成式解码器只需向前一步即可获得长序列输出,同时避免推理阶段的累积误差扩散。
2 Preliminary
我们首先提供 LSTF 问题定义。在具有固定大小窗口的滚动预测设置下,我们有输入 X t = { x 1 t , . . . , x L x t ∣ x i t ∈ R d x } X^t = \{x^t_1,..., x^t_{L_x} | x^t_i ∈ R^{d_x} \} Xt={x1t,...,xLxt∣xit∈Rdx} 在时间 t t t,输出是预测对应的序列 Y t = { y 1 t , . . . , y L y t ∣ y i t ∈ R d y } Y^t = \{y^t_1,..., y^t_{L_y} | y^t_i ∈ R^{d_y} \} Yt={y1t,...,yLyt∣yit∈Rdy}。LSTF 问题鼓励比以前的工作更长的输出长度,并且特征维度不限于单变量情况 (dy ≥ 1)。
编码器-解码器架构:许多流行的模型被设计为将输入表示 X t X^t Xt “编码”为隐藏状态表示 H t H^t Ht 并从 H t = { h 1 t , . . . , h L h t } H^t = \{h^t_1, . . . , h^t_{L_h} \} Ht={h1t,...,hLht} “解码”输出的表示 Y t Y^t Yt。推理涉及一个名为“动态解码”的分步过程,其中解码器从前一个状态 h k t h^t_k hkt 计算新的隐藏状态 h k + 1 t h^t_{k+1} hk+1t 和第 k k k 步的其他必要输出,然后预测第 ( k + 1 ) (k + 1) (k+1) 步的序列 y k + 1 t y^t_{k+1} yk+1t。
输入表示:给出统一的输入表示以增强时间序列输入的全局位置上下文和局部时间上下文。为了避免琐碎的描述,我们将详细信息放在附录 B 中。
3 Methodology
现有的时间序列预测方法可以大致分为两类。经典的时间序列模型是时间序列预测的可靠主力,深度学习技术主要开发编码器-解码器使用 RNN 及其变体进行预测范式。我们提出的 Informer 在针对 LSTF 问题的同时拥有编码器-解码器架构。请参阅图(2)的概述和详细信息以下部分。
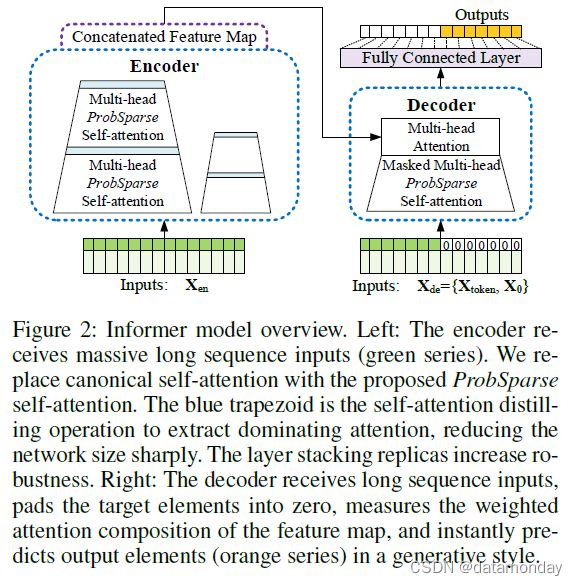
图 2:Informer 模型概述。左:编码器接收大量长序列输入(绿色)。我们用提出的 ProbSparse self-attention 替换了 canonical self-attention。蓝色梯形是提取主导注意力的自注意力蒸馏操作,大大减小了网络大小。层堆叠副本增加了鲁棒性。右图:解码器接收长序列输入,将目标元素填充为零,测量特征图的加权注意力组成,并立即以生成方式预测输出元素(橙色)。
Efficient Self-attention Mechanism
(Vaswani et al. 2017) 中的规范自注意力是基于元组输入定义的,即查询、键和值,它执行缩放的点积为 A ( Q , K , V ) = S o f t m a x ( Q K T / √ d ) V A(Q, K, V) = Softmax(QK^T/√d)V A(Q,K,V)=Softmax(QKT/√d)V,其中 Q ∈ R L Q × d Q ∈ R^{L_Q×d} Q∈RLQ×d, K ∈ R L K × d K ∈ R^{L_K×d} K∈RLK×d, V ∈ R L V × d V ∈ R^{L_V ×d} V∈RLV×d, d d d 为输入维度。为了进一步讨论自注意力机制,让 q i q_i qi、 k i k_i ki、 v i v_i vi 分别代表Q、K、V中的第 i i i 行。按照 (Tsai et al. 2019) 中的公式,第 i i i 个查询的注意力被定义为概率形式的内核平滑器:
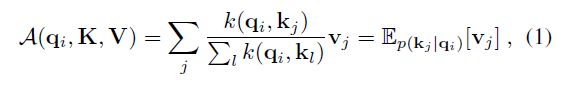
其中 p ( k j ∣ q i ) = k ( q i , k j ) / ∑ l k ( q i , k l ) p(k_j|q_i) = k(q_i, k_j)/\sum_l k(q_i, k_l) p(kj∣qi)=k(qi,kj)/∑lk(qi,kl) 和 k ( q i , k j ) k(q_i, k_j) k(qi,kj) 选择非对称指数核 e x p ( q i k j T / √ d ) exp(q_ik^T_j /√d) exp(qikjT/√d)。 self-attention 根据计算概率 p ( k j ∣ q i ) p(k_j|q_i) p(kj∣qi) 组合这些值并获取输出。它需要二次点积计算和 O ( L Q L K ) O(L_QL_K) O(LQLK) 内存使用,这是增强预测能力时的主要缺点。
之前的一些尝试表明,self-attention 概率的分布具有潜在的稀疏性,他们在不显著影响性能的情况下,在所有 p ( k j ∣ q i ) p(k_j|q_i) p(kj∣qi) 上设计了“选择性”计数策略。
- Sparse Transformer (Child et al. 2019) 结合了行输出和列输入,其中稀疏性来自分离的空间相关性。
- LogSparse Transformer (Li et al. 2019) 注意到 self-attention 的循环模式,并迫使每个单元以指数步长关注其前一个单元。
- Longformer(Beltagy、Peters 和 Cohan 2020)将前两项工作扩展到更复杂的稀疏配置。
然而,它们仅限于遵循启发式方法的理论分析,并使用相同的策略处理每个多头自注意力,这限制了它们的进一步改进。
为了激发我们的方法,我们首先对典型自我注意的学习注意模式进行定性评估。“稀疏”自注意力分数形成长尾分布(详见附录 C),即少数点积对贡献主要注意力,而其他点积对产生微不足道的注意力。那么,接下来的问题是如何区分它们呢?
Query Sparsity Measurement:从公式 (1),第 i 个查询对所有键的注意力被定义为概率 p(kj|qi),输出是它与值 v 的组合。占主导地位的点积对 (dot-product pair) 鼓励相应的查询的注意力概率分布远离均匀分布。如果 p(kj|qi) 接近于均匀分布 q(kj|qi) = 1/LK,则 self-attention 成为 V 值的一个微不足道的总和,并且对于住宅输入 (residential input) 是多余的。自然地,分布 p 和 q 之间的“相似性”可以用来区分“重要”查询。我们通过 Kullback-Leibler 散度来衡量“相似度”:
![]()
去掉常数,我们将第 i i i 个查询的稀疏性度量定义为
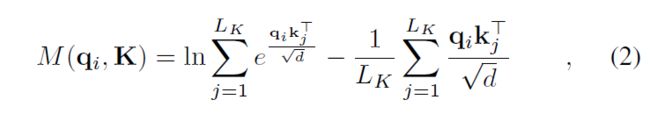
其中第一项是所有键 q i q_i qi 的 Log-Sum-Exp (LSE),第二项是它们的算术平均值。如果第 i i i 个查询获得更大的 M ( q i , K ) M(q_i, K) M(qi,K),则其注意概率 p p p 更“多样化”,并且很有可能在长尾自注意力分布的头部字段中包含占主导地位的点积对。
ProbSparse Self-attention:我们通过允许每个键只关注 u u u 个主要查询来实现 ProbSparse self-attention:

其中 Q ‾ \overline Q Q 是一个与 q q q 大小相同的稀疏矩阵,它只包含稀疏度量 M ( q , K ) M(q, K) M(q,K) 下的 Top-u 个查询。在恒定的采样因子 c c c 的控制下,我们设置 u = c ⋅ l n L Q u = c · ln L_Q u=c⋅lnLQ,这使得 ProbSparse self-attention 只需要为每个 query-key 查找计算 O ( l n L Q ) O(ln L_Q) O(lnLQ) 次点积,并且层内存使用保持 O ( L K l n L Q ) O(L_K ln L_Q) O(LKlnLQ)。在多头视角下,这种注意力为每个头生成不同的稀疏查询键对,从而避免了严重的信息丢失。
然而,遍历度量 M ( q i , K ) M(q_i, K) M(qi,K) 的所有查询需要计算每个点积对,即二次 O ( L Q L K ) O(L_QL_K) O(LQLK),此外 LSE 操作具有潜在的数值稳定性问题。受此启发,我们提出了一种用于有效获取查询稀疏度测量的经验近似值。

Top-u 的范围在与命题 1 的边界松弛中近似成立(参见附录 D.2)。在长尾分布下,我们只需要随机抽取 U = L K l n L Q U = L_K ln L_Q U=LKlnLQ 个点积对来计算 M ( q i , K ) M(q_i, K) M(qi,K),即用零填充其他对。然后,我们从中选择稀疏的 Top-u 作为 Q ‾ \overline Q Q 。 M ( q i , K ) M(q_i, K) M(qi,K) 中的最大算子对零值不太敏感,并且是数值稳定的。在实践中,查询和键的输入长度在自注意力计算中通常是等价的,即 L Q = L K = L L_Q = L_K = L LQ=LK=L 使得 ProbSparse 自注意力的总时间复杂度和空间复杂度为 O ( L l n L ) O(L ln L) O(LlnL)。
Encoder: Allowing for Processing Longer Sequential Inputs under the Memory Usage Limitation
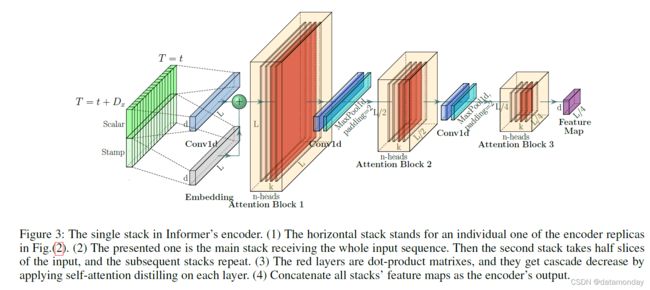
编码器旨在提取长序列输入的鲁棒远程依赖性。在输入表示之后,第 t t t 个序列输入 X t X^t Xt 已被整形为矩阵 X e n t ∈ R L x × d m o d e l X^t_{en} ∈ \R^{L_x×d_{model}} Xent∈RLx×dmodel。为了清楚起见,我们在图(3)中给出了编码器的草图。
Self-attention Distilling:作为 ProbSparse self-attention 机制的自然结果,编码器的特征图具有值 V 的冗余组合。我们使用蒸馏操作对具有主导特征的优越者进行特权,并在下一层制作聚焦的自注意特征图。它大幅修剪了输入的时间维度,在图(3)中看到了注意力块的 n 头权重矩阵(重叠的红色方块)。受 膨胀卷积(dilated convolution) 的启发,我们的“蒸馏”过程从第 j j j 层前进到第 ( j + 1 ) (j + 1) (j+1) 层,如下所示:
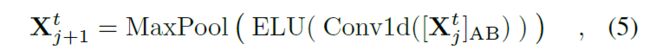
其中 [ ] AB代表注意区块。它包含多头ProbSparse自关注和基本操作,其中Conv1d()使用ELU()激活函数在时间维度上执行一维卷积滤波器(内核宽度= 3)。我们添加了一个跨度为2的最大池层,并在堆叠一个层后将Xt向下采样到它的一半切片中,这将整体内存使用减少到O((2?)L log L),哪里?是个小数目。为了增强提取操作的鲁棒性,我们使用减半的输入来构建主堆栈的副本,并通过一次丢弃一层来逐渐减少自关注提取层的数量,如图(2)中的金字塔,使得它们的输出维度对齐。因此,我们将所有堆栈的输出连接起来,得到编码器的最终隐藏表示。
其中 [ ⋅ ] A B [·]_{AB} [⋅]AB 表示注意块。它包含 Multi-head ProbSparse self-attention 和基本操作,其中 Conv1d(·) 使用 ELU(·) 激活函数(Clevert, Unterthiner, and Hochreiter 2016)。我们添加一个步幅为 2 的最大池化层,并在堆叠一层后将 X t X^t Xt 下采样到它的半片中,这将整个内存使用量减少到 O ( ( 2 − ϵ ) L l o g L ) O((2 - \epsilon)L log L) O((2−ϵ)LlogL),其中 ϵ \epsilon ϵ 是一个小数字。为了提高提取操作的鲁棒性,我们使用减半的输入构建主堆栈的副本,并通过一次删除一层来逐步减少自注意力提取层的数量,如图(2)中的金字塔,例如它们的输出维度是对齐的。因此,我们将所有堆栈的输出连接起来,并得到编码器的最终隐藏表示。
Decoder: Generating Long Sequential Outputs Through One Forward Procedure
我们在图(2)中使用标准解码器结构(Vaswani et al. 2017),它由两个相同的多头注意力层组成。然而,生成推理被用来缓解长预测中的速度骤降。我们为解码器提供以下向量:
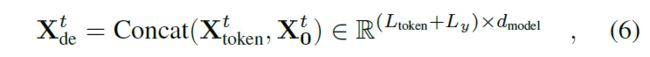
其中 X t o k e n t ∈ R L t o k e n × d m o d e l X^t_{token} ∈ \R^{L_{token}×d_{model}} Xtokent∈RLtoken×dmodel 是起始标记, X 0 t ∈ R L y × d m o d e l X^t_0 ∈ \R^{L_y×d_{model}} X0t∈RLy×dmodel 是目标序列的占位符(设置标量为 0)。通过将 masked dot-products 设置为 -∞,在 ProbSparse self-attention 计算中应用了 Masked multi-head attention。它可以防止每个位置关注即将到来的位置,从而避免自回归。全连接层获得最终输出,其大小 d y d_y dy 取决于执行的是单变量预测还是多变量预测。
Generative Inference:Start token 有效地应用于 NLP 的“动态解码”(Devlin et al. 2018),我们将其扩展为一种生成方式。我们没有选择特定的标志作为标记,而是在输入序列中采样 L t o k e n L_{token} Ltoken 长序列,例如输出序列之前的一个较早的切片。以预测 168 个点为例(实验部分的 7 天温度预测),我们将目标序列前 5 天的已知时间作为“start-token”,并将 X d e = { X 5 d , X 0 } X_{de} = \{X_{5d}, X_0\} Xde={X5d,X0}。 X 0 X_0 X0 包含目标序列的时间戳,即目标周的上下文。然后,我们提出的解码器通过一个前向过程预测输出,而不是传统编码器-解码器架构中耗时的“动态解码”。计算效率部分给出了详细的性能比较。
损失函数:我们在预测目标序列时选择MSE损失函数,损失从解码器的输出通过整个模型传播回来。
4 Experiment
Datasets
我们在四个数据集上进行了大量的实验,其中包括两个为LSTF收集的真实数据集和两个公共基准数据集。
ETT (电力变压器温度):ETT是电力长期部署中至关重要的指标。我们从中国两个独立的县收集了2年的数据。为了探索LSTF问题的粒度,我们为1小时级别和15分钟级别分别创建了{ETTh1,ETTh2}和ETTm1数据集。每个数据点由目标值“油温”和6个功率负载特性组成。训练/评估/测试是12/4/4个月。
ECL (用电负荷):收集321个客户的用电量(Kwh)。由于数据缺失,我们将数据集转换为2年的每小时消耗量,并将“MT 320”设置为目标值。训练/评估/测试是15/3/4个月。
天气:该数据集包含从2010年到2013年的4年间美国近1600个地点的当地气候数据,其中数据点每1小时收集一次。每个数据点由目标值 “wet bulb” 和11个气候特征组成。训练/评估/测试是28/10/10月。
Experimental Details
我们简要总结了基础知识,更多关于网络组件和设置的信息在附录e中给出。
**基线:我们选择了五种时间序列预测方法作为比较,包括ARIMA、Prophet 、LSTMa、LSTnet 和 DeepAR。为了更好地探索 ProbSparse 自注意力在 Informer 中的表现,我们在实验中结合了规范的 self-attention 变体 (Informer†)、有效的变体 Reformer (Kitaev、Kaiser 和 Levskaya 2019) 以及最相关的工作 LogSparse self-attention (Li et al. 2019)。网络组件的详细信息在附录E.1中给出。
超参数调整:我们对超参数进行网格搜索,详细范围在附录E.3中给出。Informer在编码器中包含一个3层堆栈和一个1层堆栈(1/4输入),以及一个2层解码器。我们提出的方法用 Adam 优化器进行优化,其学习率从 1e-4 开始,每个 epoch 衰减两倍。适当提前停止时,总周期数为8。我们按照推荐的方式设置比较方法,批量为32。
设置:每个数据集的输入都是零均值归一化的。
在 LSTF 设置下,我们逐步延长预测窗口大小 Ly,即 {ETTh, ECL, Weather} 中的 {1d, 2d, 7d, 14d, 30d, 40d},{6h, 12h, 24h, 72h, 168h} ETTM。
评估指标:我们在每个预测窗口上使用两个评估度量,包括 MSE 和 MAE(多变量预测求平均值),并以 stride = 1 滚动整个集合。
平台:所有模型均在单个 Nvidia V100 32GB GPU 上进行训练/测试。源代码可在 https://github.com/zhouhaoyi/Informer2020 获取。
Results and Analysis
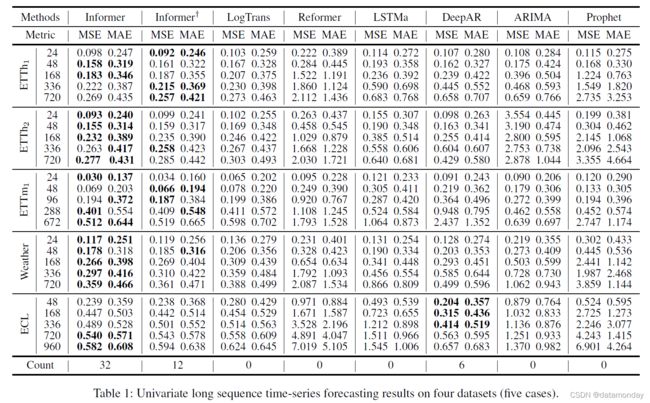
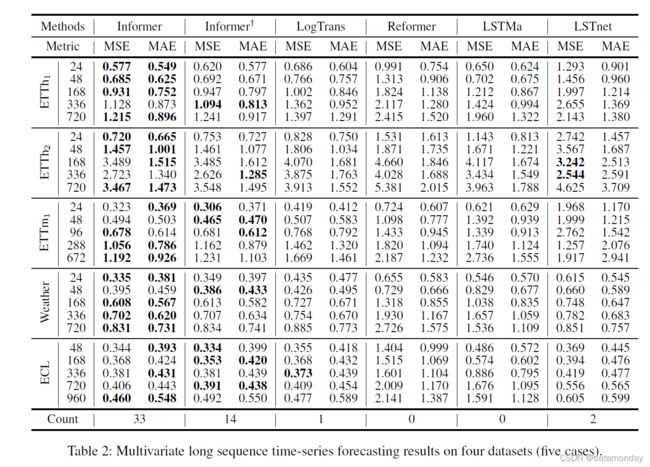
表1和表2总结了所有方法在4个数据集上的单变量/多变量评估结果。随着对预测能力的更高要求,我们逐渐延长预测范围,其中LSTF问题设置被精确控制,以便在单个GPU上对每种方法进行处理。最佳结果以粗体突出显示。
单变量时间序列预测
单变量时间序列预测 在此设置下,每种方法都将预测作为时间序列上的单个变量。从表 1 中,我们可以观察到:
- 1)所提出的模型 Informer 显着提高了所有数据集的推理性能(最后一列中的获胜计数),并且 Informer 预测误差在不断增长的预测范围内平稳而缓慢地上升,这表明 Informer 在提高 LSTF 问题的预测能力方面的成功。
- 2)Informer 击败了它的规范退化 Informer†,主要是在获胜计数上,即 32>12,这支持查询稀疏假设,提供可比较的注意力特征图。我们提出的方法也优于最相关的工作 LogTrans 和 Reformer。我们注意到,Reformer 保持动态解码并且在 LSTF 中表现不佳,而其他方法受益于作为非自回归预测器的生成式解码器。
- 3)Informer 模型显示出明显优于循环神经网络 LSTMa 的结果。我们的方法的 MSE 降低了 26.8%(在 168)、52.4%(在 336)和 60.1%(在 720)。这揭示了自注意力机制中较短的网络路径比基于 RNN 的模型获得了更好的预测能力。
- 4)所提出的方法在 MSE 上优于 DeepAR、ARIMA 和 Prophet,平均降低了 49.3%(168 处)、61.1%(336 处)和 65.1%(720 处)。在 ECL 数据集上,DeepAR 在较短的视野 (≤ 336) 上表现更好,我们的方法在较长的视野上表现更好。我们将此归因于一个具体的例子,其中预测能力的有效性通过问题的可扩展性来体现。
多变量时间序列预测
在这种情况下,一些单变量方法是不合适的,而 LSTnet 是最先进的基线。相反,我们提出的 Informer 通过调整最终的 FCN 层很容易从单变量预测变为多变量预测。从表 2 中,我们观察到:
- 1)所提出的模型 Informer 大大优于其他方法,单变量设置中的结果 1 和 2 对于多变量时间序列仍然成立。
- 2)Informer 模型的结果优于基于 RNN 的 LSTMa 和基于 CNN 的 LSTnet,MSE 平均下降 26.6%(168 处)、28.2%(336 处)、34.3%(720 处)。与单变量结果相比,压倒性的性能降低了,这种现象可能是由于特征维度预测能力的各向异性造成的。这超出了本文的范围,我们将在以后的工作中进行探索。
Parameter Sensitivity
我们在单变量设置下对 ETTh1 上提出的 Informer 模型进行敏感性分析。
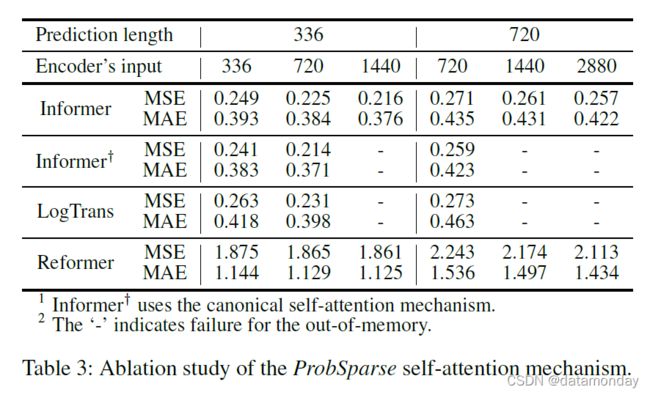
- 输入长度:在图(4a)中,当预测短序列(如 48)时,最初增加编码器/解码器的输入长度会降低性能,但进一步增加会导致 MSE 下降,因为它会带来重复的短期模式。然而,在预测长序列(如 168)时,MSE 会随着更长的输入而降低。因为较长的编码器输入可能包含更多的依赖关系,而较长的解码器标记具有丰富的局部信息。
- Sampling Factor:采样因子控制 Eq.(3) 中 ProbSparse self-attention 的信息带宽。我们从小的因子(=3)开始到大的因子,总体性能略有提高并最终稳定在图(4b)中。它验证了我们的查询稀疏假设,即自注意机制中存在冗余点积对。我们在实践中设置采样因子 c = 5(红线)。
- 层堆叠的组合:层的副本是自注意力蒸馏的补充,我们在图(4c)中研究了每个堆叠 {L,L/2,L/4} 的行为。较长的堆叠对输入更敏感,部分原因是接收更多的长期信息。我们方法的选择(红线),即加入 L 和 L/4,是最稳健的策略。
Ablation Study: How well Informer works?
我们还在考虑消融的情况下对 ETTh1 进行了额外的实验。
ProbSparse self-attention 机制的性能
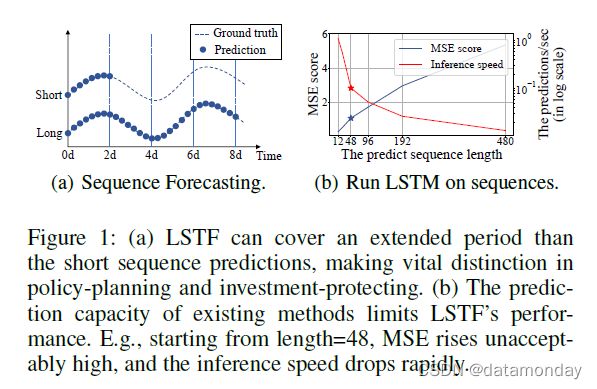
在整体结果表 1 和表 2 中,我们限制了问题设置,以使内存使用对于规范自注意是可行的。在这项研究中,我们将我们的方法与 LogTrans 和 Reformer 进行了比较,并深入探讨了它们的极端性能。为了隔离内存效率问题,我们首先将设置减少为 {batch size=8,heads=8,dim=64},并在单变量情况下保持其他设置。在表 3 中,ProbSparse self-attention 表现出比同类产品更好的性能。LogTrans 在极端情况下会出现 OOM,因为它的公共实现是全注意力的掩码,仍然有 O(L2) 的内存使用。我们提出的 ProbSparse self-attention 避免了这种情况,因为 Eq.(4) 中的查询稀疏假设带来的简单性,参考附录 E.2 中的伪代码,并达到了更小的内存使用量。
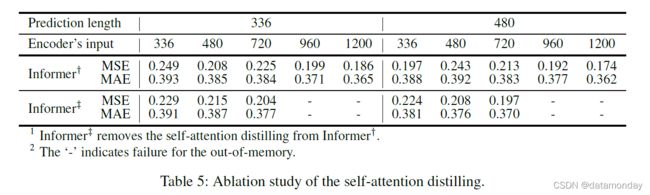
在本研究中,我们使用 Informer† 作为基准来消除 ProbSparse 自注意力的额外影响。另一个实验设置与单变量时间序列的设置一致。从表 5 中可以看出,Informer† 完成了所有实验,并在利用长序列输入后取得了更好的性能。比较方法 Informer‡ 去除了蒸馏操作并以更长的输入 (> 720) 达到 OOM。关于长序列输入在 LSTF 问题中的好处,我们得出结论,自注意力蒸馏值得采用,尤其是在需要更长的预测时。
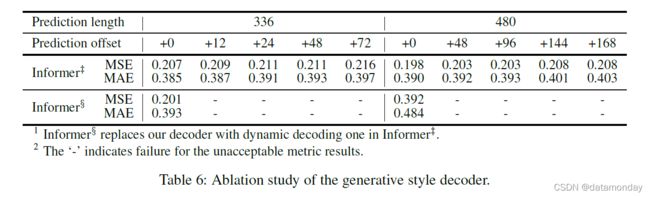
生成风格解码器的性能
在这项研究中,我们证明了我们的解码器在获得“生成”结果方面的潜在价值。与现有方法不同,标签和输出在训练和推理中被迫对齐,我们提出的解码器的预测仅依赖于时间戳,它可以通过偏移量进行预测。从表 6 可以看出,Informer‡ 的一般预测性能随着偏移量的增加而抵抗,而对应的动态解码失败。它证明了解码器能够捕捉任意输出之间的个体长程相关性(individual long-range dependency),并避免误差累积。
Computation Efficiency
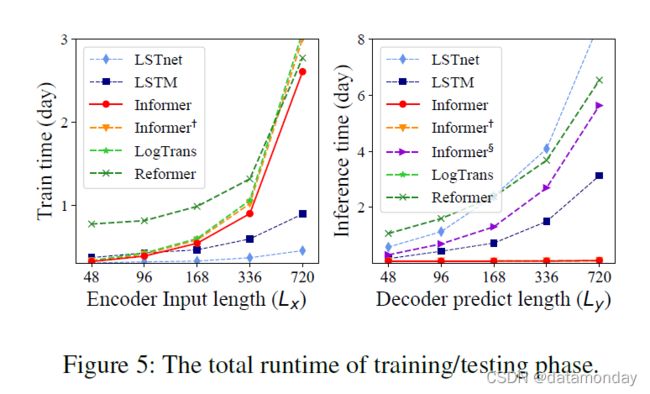
通过多元设置和所有方法当前最好的实现,我们在图(5)中进行了严格的运行时比较。在训练阶段,Informer(红线)在基于 Transformer 的方法中实现了最好的训练效率。在测试阶段,我们的方法比生成式解码的其他方法快得多。表 4 总结了理论时间复杂度和内存使用情况的比较。Informer 的性能与运行时实验一致。请注意,LogTrans 专注于改进 self-attention 机制,我们在 LogTrans 中应用我们提出的解码器以进行公平比较(表 4)。

5 Conclusion
在本文中,我们研究了长序列时间序列预测问题,并提出了 Informer 来预测长序列。具体来说,我们设计了 ProbSparse self-attention 机制和蒸馏操作来处理 vanilla Transformer 中的二次时间复杂度和二次内存使用的挑战。此外,精心设计的生成解码器缓解了传统编码器-解码器架构的限制。真实世界数据的实验证明了 Informer 在提高 LSTF 问题的预测能力方面的有效性。
Appendices
Appendix A Related Work
我们在下面提供了长序列时间序列预测 (LSTF) 问题的文献综述。
时间序列预测
现有的时间序列预测方法可以大致分为两类:
- 经典模型。经典时间序列模型是时间序列预测的可靠主力,具有可解释性和理论保证等吸引人的特性(Box et al. 2015; Ray 1990)。现代扩展包括对缺失数据(Seeger et al. 2017)和多种数据类型(Seeger、Salinas 和 Flunkert 2016)的支持。
- 基于深度学习的方法。基于深度学习的方法主要通过使用 RNN 及其变体开发序列到序列预测范式,实现了突破性的性能。尽管取得了实质性进展,但现有算法仍然无法以令人满意的精度预测长序列时间序列。典型的最先进的方法,尤其是深度学习方法,仍然是一个循序渐进的序列预测范式,具有以下局限性:
- i)即使它们可以实现一步的准确预测向前,它们经常遭受动态解码的累积误差,导致 LSTF 问题的误差很大(Liu et al. 2019; Qin et al. 2017)。预测精度随着预测序列长度的增加而衰减。
- ii)由于梯度消失和记忆约束的问题(Sutskever, Vinyals, and Le 2014),大多数现有方法无法从整个时间序列历史的过去行为中学习。在我们的工作中,Informer 旨在解决这两个限制。
长序列输入问题
从上面的讨论中,我们提到了关于长序列时间序列输入(LSTI)问题的第二个限制。我们将探索相关工作并在我们的 LSTF 问题之间进行比较。研究人员在实践中截断/汇总/采样输入序列以处理非常长的序列,但在做出准确预测时可能会丢失有价值的数据。
- 截断 BPTT(Aicher, Foti, and Fox 2019)不修改输入,而是仅使用最后一个时间步来估计权重更新中的梯度
- 辅助损失(Trinh et al. 2018)通过添加辅助梯度来增强梯度流。
- Recurrent Highway Networks (Zilly et al. 2017) 和 Bootstrapping Regularizer (Cao and Xu 2019)。这些方法试图改善循环网络长路径中的梯度流,但随着 LSTI 问题中序列长度的增长,性能受到限制。
- 基于 CNN 的方法(Stoller et al. 2019; Bai, Kolter, and Koltun 2018)使用卷积滤波器来捕获长期依赖关系,并且它们的感受野随着层的堆叠呈指数增长,这会损害序列对齐。在 LSTI 问题中,主要任务是增强模型接收长序列输入的能力,并从这些输入中提取长程依赖关系。但是 LSTF 问题寻求增强模型预测长序列输出的预测能力,这需要建立输出和输入之间的长期依赖关系。因此,上述方法直接用于 LSTF 是不可行的。
注意力模型
(Bahdanau, Cho, and Bengio 2015)首先提出了加性注意力来改善编码器-解码器架构在翻译任务中的词对齐。然后,(Luong, Pham, and Manning 2015)提出了它的变体——广泛使用的位置、一般和点积注意力。流行的基于 self-attention 的 Transformer (Vaswani et al. 2017) 最近被提出作为序列建模的新思路,并取得了巨大的成功,尤其是在 NLP 领域。通过将其应用于翻译、语音、音乐和图像生成,已经验证了更好的序列比对能力。在我们的工作中,Informer 利用其序列比对能力,使其适应 LSTF 问题。
基于 Transformer 的时间序列模型
最相关的工作(Song et al. 2018; Ma et al. 2019; Li et al. 2019)都是从在时间序列数据中应用 Transformer 开始的,但在 LSTF 预测中失败了,因为它们使用原生的 Transformer。以及其他一些工作(Child et al. 2019; Li et al. 2019)注意到自注意力机制的稀疏性,我们在主要背景下对其进行了讨论。
Appendix B The Uniform Input Representation
RNN 模型(Schuster and Paliwal 1997; Hochreiter and Schmidhuber 1997; Chung et al. 2014; Sutskever, Vinyals, and Le 2014; Qin et al. 2017; Chang et al. 2018)通过循环结构捕获时间序列模式本身,几乎不依赖时间戳。 vanilla Transformer(V aswani et al. 2017; Devlin et al. 2018)使用逐点自我注意机制,时间戳用作局部位置上下文。然而,在 LSTF 问题中,获取长距离独立性的能力需要全局信息,例如分层时间戳(周、月和年)和不可知的时间戳(假期、事件)。这些在规范的自注意力中几乎没有被利用,因此编码器和解码器之间的查询键不匹配会导致预测性能的潜在下降。我们提出了一个统一的输入表示来缓解这个问题,图(6)给出了一个直观的概述。
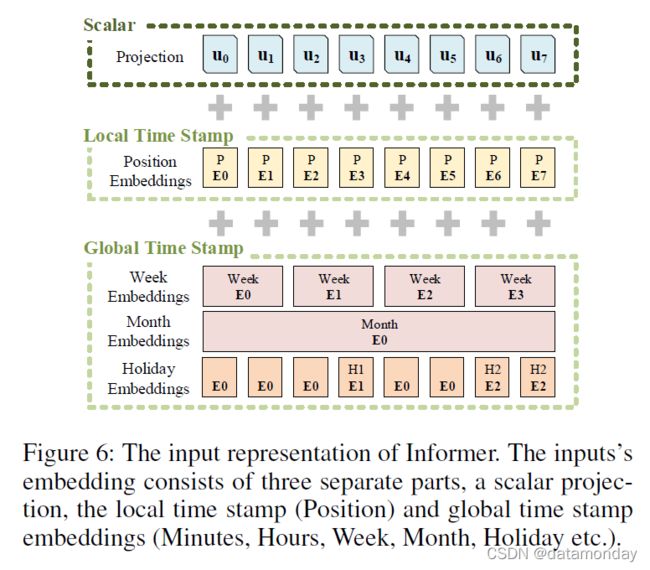
假设我们有 t-th 序列输入 X t X^t Xt 和 p p p 类型的全局时间戳,输入表示后的特征维度是 d m o d e l d_{model} dmodel。我们首先通过使用固定位置嵌入来保留本地上下文:
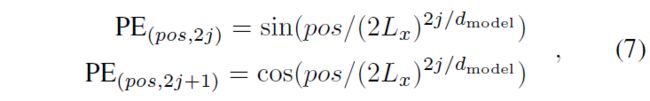
其中 j ∈ { 1 , . . . , ⌊ d m o d e l / 2 ⌋ } j ∈ \{1, . . . , \lfloor d_{model}/2 \rfloor \} j∈{1,...,⌊dmodel/2⌋}。每个全局时间戳都由具有有限词汇大小(最多 60 个,即以分钟为最细粒度)的可学习时间戳嵌入 SE(pos) 使用。也就是说,self-attention 的相似性计算可以访问全局上下文,并且计算消耗在长输入上是可以承受的。为了对齐维度,我们使用一维卷积滤波器(卷积核宽度=3,步幅=1)将标量上下文 x i t x^t_i xit 投影到 d m o d e l d_{model} dmodel 维的向量 u i t u^t_i uit 中。因此,我们有馈送向量

其中 i ∈ {1, . . . , Lx},α 是平衡标量投影和局部/全局嵌入之间幅度的因子。如果序列输入已经标准化,我们建议 α = 1。
Appendix C The long tail distribution in self-attention feature map
我们在 ETTh1 数据集上执行了 vanilla Transformer 来研究自注意力特征图的分布。我们选择 {Head1,Head7}@Layer1 的注意力分数。图(7)中的蓝线形成了一个长尾分布,即少数点积对贡献了主要注意力,其他可以忽略不计。

Appendix D Details of the proof
略过了
Appendix E Reproducibility
实验细节
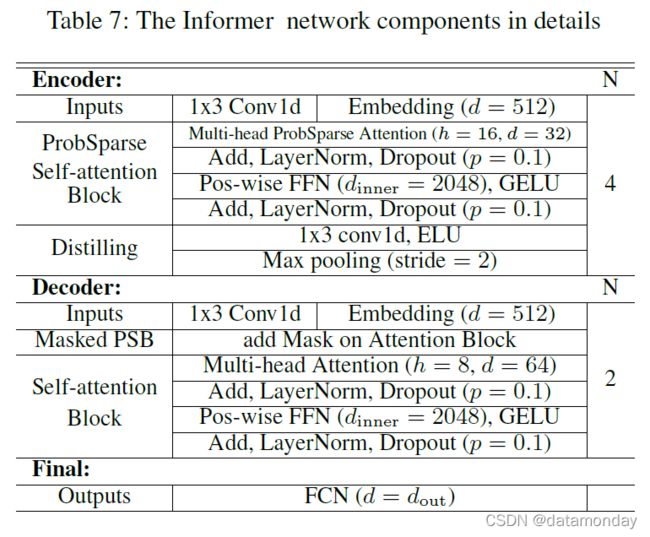
表 7 总结了所提出的 Informer 模型的详细信息。对于 ProbSparse 自注意力机制,我们让 d=32,n=16 并添加残差连接,一个位置前馈网络层(内层维度为 2048)和一个 dropout 层 (p = 0.1)。请注意,我们为每个数据集保留 10% 的验证数据,因此所有实验都是在 5 次随机训练/验证移位选择上进行的,并且结果是 5 次运行的平均值。所有数据集都进行了标准化,使得变量的平均值为 0,标准差为 1。
ProbSparse 自注意力的实现
我们已经使用 Pytorch 1.0 在 Python 3.6 中实现了 ProbSparse 自注意力。伪代码在 Algo.(1) 中给出。源代码在 https://github.com/zhouhaoyi/Informer2020。所有过程都可以进行高效的向量运算并保持对数的总内存使用量。可以通过在步骤6中应用位置掩码并在步骤7的mean()中使用cmusum()来实现掩码版本。在实践中,我们可以使用sum()作为mean()的更简单的实现。

超参数调整范围
对于所有方法,对于ETTh1、ETTh2、天气和电力数据集,递归分量的输入长度选自{24,48,96,168,336,720},对于ETTm数据集,选自{24,48,96,192,288,672}。LSTMa 和DeepAR,隐藏状态的大小选自{32,64,128,256}。对于 LSTnet,递归层和卷积层的隐藏维度从 {64,128,256} 和 {32,64,128} 中选择,对于递归跳过层,对于ETTh1、ETTh2、天气和ECL数据集,递归跳过层的跳过长度设置为24,对于ETTm数据集,设置为96。对于 Informer,编码器的层选自{6,4,3,2},解码器的层设置为2。多头注意力的头数从{8,16}中选取,多头注意力输出的维数设为512。对于ETTh1、ETTh2、天气和ECL数据集,编码器输入序列和解码器起始标记的长度选自{24,48,96,168,336,480,720},对于ETTm数据集,选自{24,48,96,192,288,480,672}。在实验中,解码器的起始标记是从编码器的输入序列中截取的一段,因此解码器的起始标记长度必须小于编码器的输入长度。
基于RNN的方法通过在预测窗口上左移来执行动态解码。我们提出的方法Informer-series和LogTrans(我们的解码器)执行非动态解码。
Appendix F Extra experimental results
图(9)显示了8个模型的预测切片。
- 最相关的工作 LogTrans 和 Reformer 显示出可接受的结果。
- LSTMa模型不适用于长序列预测任务。
- ARIMA和DeepAR可以捕捉长序列的长期趋势。
- Prophet 发现了变化点,并用比ARIMA和DeepAR更好的平滑曲线拟合它。
- 我们提出的模型Informer和Informer+显示出明显优于上述方法的结果。