CycleGAN学习笔记

CycleGAN学习笔记

一、CycleGAN的应用

风格迁移、物体转换、季节转换等。

作用：让两个 domain 的图片互相转化

二、CycleGAN和pix2pix的不同：

unpaired,即不用配对就可以训练。

三、GAN——Generative Adversarial Networks

2.1. 传统的GAN是 A→B 单向的：

目的： 把 domain A 的图片转化为 domain B 的图片。
网络中有生成器G（generator）和鉴别器（Discriminator）。
缺点：单纯的使用判别损失是无法进行训练的。原因在于，映射F完全可以将所有x都映射到y空间的同一张图片，使损失无效化。为此提出循环GAN网络。从域x生成域y，再从y生成回x，循环往复。例如：斑马到马。生成的马和斑马形状不同，但是马，也能骗过鉴别器。

3.2 GAN损失

训练这个单向GAN需要两个loss：生成器的重建Loss和判别器的判别Loss。
（1）重建Loss：
希望生成的图片与原图a尽可能的相似。采取 L1 loss 或者 L2 loss。

（2）判别Loss：
生成的假图片和原始真图片都会输入到判别器中。公式为0,1二分类的损失。
一　对于判别损失的理解：介绍一下价值函数：
解释：x服从数学公式: p_data(x)}分布，x是从真是数据中采样的。数学公式: p_(z)}可以是正态分布，也可以是均值分布。D(G(z))代表判别器对生成器合成数据的概率判断。E表示对所有x,z的平均。数学公式: max_{D} 指D的目标是最大化价值V，即最大化log。log在底数>1时为单调递增函数。

四.CycleGAN

CycleGAN本质上是两个镜像对称的GAN，构成了一个环形网络。
两个GAN共享两个生成器，并各自带一个判别器，即共有两个判别器和两个生成器。
即：两个生成器网络：G和F；两个鉴别器网络：Dx和Dy。整个网络是一个对偶结构。

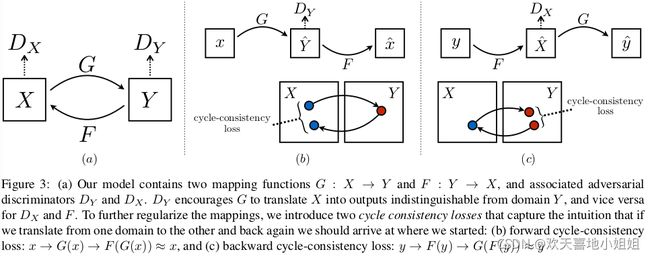
4.1整体网络结构

4.2 CycleGAN损失

涉及4种损失函数：G网络、D网络、Cycle loss、Identity loss
X→Y 的判别器损失为：
Y→X 的判别器损失为：
循环一致性损失()为：
通常称为L1loss
其中，G的输入一般为x，是用来生成fake y图的生成器，F的输入一般为y，是用来生成fake x图的生成器。当我们把x送入到G中后，得到的是假的y图，再把这张假的y图送入到F中，得到更假的x图。理想情况下，此时的更假的x图应该与原始的x图相差无几。这样也便构成了一个循环，因此叫做循环一致性损失。
在训练中经常会碰到这样一种情况，通过x得到的fake y，会越来越倾向于成为一个能骗得过判别器的值，生成器会慢慢发现，不管送进来的x是什么样，只要我生成的图越像y，就越能骗过判别器，因此只要生成跟y一样的图就好了，但这样的y是我们不想要的。即：生成器和判别器会一起欺骗网络。因此，设计了这个循环一致性损失。

网络的所有损失加起来为：

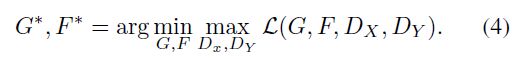Identity loss:(容易忽略)
生成器G用来生成y风格图像，那么把y送入G，应该仍然生成y，只有这样才能证明G具有生成y风格的能力。因此G(y)和y应该尽可能接近。根据论文中的解释，如果不加该loss，那么生成器可能会自主地修改图像的色调，使得整体的颜色产生变化。

五.PatchGAN

PatchGAN其实指的是GAN的判别器，类似与全卷积网络。

![在这里插入图片描述](https://img-blog.csdnimg.cn/e36937004f3c437ba4d28a9ecb1186a4.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5qyi5aSp5Zac5Zyw5bCP5aeQ5aeQ,size_16,color_FFFFFF,t_70,g_se,x_16#pic_center

5.1 与普通ＧＡＮ判别器的区别：

**普通的GAN判别器：**将输入映射成一个实数，即输入样本为真样本的概率。是对生成器生成的整幅图像的一个评价。
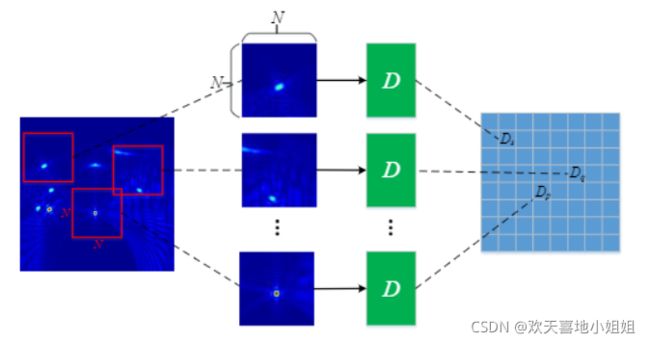
**PatchGAN：**将输入映射为NxN的patch(矩阵)Ｘ， 数学公式: X_{ij}的值代表每个patch为真样本的概率，将 数学公式: X_{ij}求均值，即为判别器最终输出。

5.2 优点：

X 其实就是卷积层输出的特征图。从这个特征图可以追溯到原始图像中的某一个位置，可以看出这个位置对最终输出结果的影响。即：最终结果求平均，考虑到图像的不同部分的影响。

5.3 适用场景：

对于要求高分辨率、高清细节的图像领域中。
原因：引入了PatchGAN，它的感受域对于与输入中的一小块区域，也就是说， 数学公式: X_{ij} 对应了判别器对输入图像的一小块的判别输出，这样训练使模型更能关注图像细节。普通GAN判别器不适合。

5.4 网络结构：

##网络结构:
Conv2d(3, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)), LeakyReLU 
Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)), BN+LeakyReLU
Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)), BN+LeakyReLU
Conv2d(256, 512, kernel_size=(4, 4), stride=(1, 1), padding=(1, 1)), BN+LeakyReLU
Conv2d(512, 1, kernel_size=(4, 4), stride=(1, 1), padding=(1, 1))
##最后一层的输出通道数是512→1，该处的通道变化即形成了一个N*N*1的矩阵特征图。

代码的最后附上了PatchGAN的网络结构，大家可以自己尝试调试一下。注意到最后一层的输出通道数是512→1，该处的通道变化即形成了一个NN1的矩阵特征图。
另外在大神Phillip Isola的回答中（文末有链接）提到最后的特征图矩阵中的一个piexl对应原图的7070piexls，这也可以在代码中计算得到，即特征图的一个点的感受野对应原图7070区域。大家可以根据网络结构推理70*70感受野怎么来的，这里贴出Fomoro AI软件计算的感受野用以佐证。

5.5 感受域

对CycleGAN来说，判别器输出大小30x30x1，论文中却指出PatchGAN输入图像处理为70x70patches，就是根据判别器最终输出的特征图进行回溯，最终对应到输入图像70x70的区域．
为了便于理解，看下面的代码，其计算感受域大小

def f(output_size, ksize, stride):
    return (output_size - 1) * stride + ksize
last_layer = f(output_size=1, ksize=4, stride=1)
# Receptive field: 4
fourth_layer = f(output_size=last_layer, ksize=4, stride=1)
# Receptive field: 7
third_layer = f(output_size=fourth_layer, ksize=4, stride=2)
# Receptive field: 16
second_layer = f(output_size=third_layer, ksize=4, stride=2)
# Receptive field: 34
first_layer = f(output_size=second_layer, ksize=4, stride=2)
# Receptive field: 70
print(f'最后一层感受域大小:{last_layer}')
print(f'第一层感受域大小:{first_layer}')
#最后一层感受域大小:4
#第一层感受域大小:70

f即为计算卷积感受域的公式，最后一层的感受域即为卷积核大小4，那么这个卷积核能够感受到原始输入图像多大的范围呢？是70，也就是CycleGAN所说的70x70patches.
综上，PatchGAN并不神秘，其只是一个全卷积网络而已，只是最终输出是一个特征图X，而非一个实数.它就相当于对图像先进行若干次70x70的随机剪裁，将剪裁后图像输入普通的判别器，然后对所有输出的实数值取平均．

5.6PatchGAN的实现

class NLayerDiscriminator(nn.Module):
    """Defines a PatchGAN discriminator"""
    def __init__(self, input_nc, ndf=64, n_layers=3, norm_layer=nn.BatchNorm2d):
        """Construct a PatchGAN discriminator
        Parameters:
            input_nc (int)  -- the number of channels in input images
            ndf (int)       -- the number of filters in the last conv layer
            n_layers (int)  -- the number of conv layers in the discriminator
            norm_layer      -- normalization layer
        """
        super(NLayerDiscriminator, self).__init__()
        if type(norm_layer) == functools.partial:  # no need to use bias as BatchNorm2d has affine parameters
            use_bias = norm_layer.func == nn.InstanceNorm2d
        else:
            use_bias = norm_layer == nn.InstanceNorm2d
        kw = 4
        padw = 1
        sequence = [nn.Conv2d(input_nc, ndf, kernel_size=kw, stride=2, padding=padw), nn.LeakyReLU(0.2, True)]
        nf_mult = 1
        nf_mult_prev = 1
        for n in range(1, n_layers):  # gradually increase the number of filters
            nf_mult_prev = nf_mult
            nf_mult = min(2 ** n, 8)
            sequence += [
                nn.Conv2d(ndf * nf_mult_prev, ndf * nf_mult, kernel_size=kw, stride=2, padding=padw, bias=use_bias),
                norm_layer(ndf * nf_mult),
                nn.LeakyReLU(0.2, True)
            ]
        nf_mult_prev = nf_mult
        nf_mult = min(2 ** n_layers, 8)
        sequence += [
            nn.Conv2d(ndf * nf_mult_prev, ndf * nf_mult, kernel_size=kw, stride=1, padding=padw, bias=use_bias),
            norm_layer(ndf * nf_mult),
            nn.LeakyReLU(0.2, True)
        ]
        sequence += [nn.Conv2d(ndf * nf_mult, 1, kernel_size=kw, stride=1, padding=padw)]  # output 1 channel prediction map
        self.model = nn.Sequential(*sequence)
    def forward(self, input):
        """Standard forward."""
        return self.model(input)

参考资料：1.https://zhuanlan.zhihu.com/p/359287990
2. https://blog.csdn.net/weixin_35576881/article/details/88058040
3. https://link.zhihu.com/?target=https%3A//github.com/junyanz/pytorch-CycleGAN-and-pix2pix/issues/39