语音识别入门第二节:语音信号处理及特征提取
目录
数字信号处理基础
基础知识
傅里叶分析
常用特征提取
特征提取流程
Fbank
MFCC
数字信号处理基础
基础知识
模拟信号到数字信号转化(ADC):在科学和工程中,遇到的大多数信号都是连续的模拟信号,而计算机只能处理离散的信号,因此,必须对这些连续的模拟信号进行转化,通过采样和量化,转化成数字信号。
以正弦波为例:有![]() ,
,![]() 为信号本身的频率,
为信号本身的频率,![]() 为时间,对该正弦波进行采样时,每隔
为时间,对该正弦波进行采样时,每隔![]() 秒进行一次采样,可以得到采样后的离散信号为
秒进行一次采样,可以得到采样后的离散信号为![]() ,
,![]() 为采样周期,
为采样周期,![]() 为采样率,n为离散证书序列。
为采样率,n为离散证书序列。
频率混叠:不同频率的正弦波经过采样后可能出现完全相同的离散信号,这种现象就是频率混叠。
奈奎斯特采样定律:采样频率大于信号中最大频率的两倍,即在原始信号的一个周期内,至少要次采样两个点,才能有效杜绝频率混叠问题。
傅里叶分析
为什么要进行离散傅里叶变换(DFT)?
DFT的作用是将时域信号变换到频域,并分析信号中的频率成分。以时域为横轴时,可以看到信号随时间变化的规律,若果将多个频率的信号叠加到一起,此时将无法分析该信号中有哪些频率成分,若以频域为横轴时,可以很容易的看到信号中有哪些频率成分。
什么信号可以进行DFT?
时域离散且周期的信号。
非周期离散信号能否进行DFT?
非周期离散信号需要进行周期延拓才可以进行DFT。即将当前信号看做整个信号的一个周期,进而进行DFT。
什么是DFT?
其中![]() ,
,![]() 为自然对数底,
为自然对数底,![]() 为DFT的第m个输出。
为DFT的第m个输出。
DFT的性质
性质1:对称性,对于实数信号,有![]()
性质2:![]() 实际上表示的是“谱密度”,如果对一个幅度为A的正弦波进行N点DFT,则DFT之后,对应频率上的幅度M和A之间的关系为:
实际上表示的是“谱密度”,如果对一个幅度为A的正弦波进行N点DFT,则DFT之后,对应频率上的幅度M和A之间的关系为:![]()
性质2:线性,如果![]() ,则对应的频域上有
,则对应的频域上有![]() 。
。
性质3:时移性,对![]() 左移k个采样点,得到的
左移k个采样点,得到的![]() ,对
,对![]() 进行DFT,有
进行DFT,有![]() 。
。
DFT的频率轴
频率分辨率:![]() ,标识最小的频率间隔。当N越大时,频率分辨率越高,在频域上,第m个点所表示的分析频率为
,标识最小的频率间隔。当N越大时,频率分辨率越高,在频域上,第m个点所表示的分析频率为![]()
快速傅里叶变换(FFT)
FFT的基本思想是把原始的N点序列,依次分解成一系列的短序列。充分利用DFT计算式中指数因子所具有的对称性质和周期性质,进而求出这些短序列相应的DFT并进行适当组合,达到删除重复计算,减少乘法和简化结构的目的。(推荐教材:Understanding DSP,第四章;数字信号处理,理论、算法与实现,第二版,清华大学出版社)
常用特征提取
Fband和MFCC特征提取流程
 特征提取流程
特征提取流程
Fbank和MFCC特征目前仍是主要使用的特征,虽然有工作尝试直接使用波形建模,但是效果并没有超越基于频域的特征。
预加重
预加重是为了提高信号高频部分的能量,高频信号在传递过程中,衰减较快,但高频部分又蕴含很多对语音识别有利的特征,因此,在特征提取部分,需要提高高频部分能量。
预加重滤波器是一个一阶高通滤波器,给定时域输入信号![]() ,预加重之后的信号为:
,预加重之后的信号为:![]() ,其中
,其中![]() 的取值一般为
的取值一般为![]() 。
。
加窗分帧
语音信号是一种非平稳的信号,但语音信号又有一个短时平稳的属性,在进行语音识别的时候,对于一句话,识别的过程也是以比较小的发音单元为单位进行识别,因此用滑动窗来提取短时片段。
对于采样率为16KHz的信号,帧长、帧移一般为25ms、10ms,即400和160个采样点。
分帧的过程即在时域上,用一个窗函数和原始信号进行相乘![]() ,
,![]() 称为窗函数,常用的窗函数有矩形窗
称为窗函数,常用的窗函数有矩形窗![]() 、汉明窗
、汉明窗![]() 。
。
加窗的过程实际是在时域上将信号截断,窗函数与信号在时域相乘,等于对于的频域表示进行卷积,矩形窗主瓣窄,但是旁瓣大,将其与原始信号的频域标识进行卷积,就会导致频率泄露。
傅里叶变换
将上一步分帧的语音帧,由时域变换到频域,去DFT系数的模,得到谱特征。
梅尔滤波器组合对数操作
梅尔滤波器组是一种符合人耳听觉的一种滤波器组。DFT得到了每个频带上信号的能量,但是人耳对频率的感知不是等间隔的,近似与对于函数。
梅尔三角滤波器组可以根据起始频率、中间频率和截止频率确定各滤波器的系数。
梅尔滤波器组设计:
- 确定滤波器组个数P
- 根据采样率
 ,DFT点数N,滤波器个数P,在梅尔域上等间隔的产生每个滤波器的起始频率、中间频率和截止频率。上一个滤波器的中间品率为下一个滤波器的起始频率。
,DFT点数N,滤波器个数P,在梅尔域上等间隔的产生每个滤波器的起始频率、中间频率和截止频率。上一个滤波器的中间品率为下一个滤波器的起始频率。 - 将梅尔域上每个三角滤波器的起始、中间、截止频率转换线性频率域,并对DFT之后的谱特征进行滤波,得到P个滤波器组能量,进行log操作,得到Fbank特征。
MFCC特征在Fbank特征基础上继续进行IDFT变换等操作。
Fbank滤波器组公式:
m表示第m个滤波器组,k表示第k个频率点,f(m)表示第m个滤波器组的起始频率对应的索引值。
倒谱分析
动态特征计算
能量计算
最简单的为:![]()
Fbank
Fbank特征一般用于DNN训练。
MFCC
一般常用的MFCC特征为39维,包括:
- 12维原始MFCC
- 12维

- 12维


- 1维能量
- 1维能量
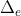
- 1维能量
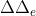
MFCC特征一般用于对角GMM训练,各维度之间相关性小。
本节实践见:语音识别入门第二节:语音信号处理及特征提取(实战篇)_安静_xju的博客-CSDN博客
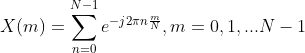
![X(m)=\sum_{n=0}^{N-1}x(n)[\cos(\frac{2\pi nm}{N})-j\sin(\frac{2\pi nm}{N})]](http://img.e-com-net.com/image/info8/f06927f22f8d4704890c13b688a05bb4.gif)