隐马尔卡夫模型(HMM)解决预测问题(多语言算法实现)
隐马尔卡夫模型(HMM)解决预测问题(多语言算法实现)
隐马尔卡夫模型(HMM)
隐马尔卡夫模型(HMM)是一种统计学模型,模型包含一条隐藏状态的马尔可夫链以及每个隐藏状态所对应的可观测状态。根据模型中的参数(隐藏状态相互转移概率、隐藏状态下不同观测状态发生的概率)可以对隐藏状态信息、观测状态信息或者某一状态链发生概率做出预测。
马尔卡夫链
马尔卡夫链表示的是一种状态空间内从一个状态转移到另一个状态的随机过程。在隐马尔可夫模型中,隐藏状态的转移就是一条马尔卡夫链。为了更好地理解HMM模型,需要了解马尔卡夫链的以下特点:
无记忆性 :马尔卡夫链中从当前状态出发,下一状态将去向何方仅与当前状态有关,与先前时刻的所有状态均无关。前往下一状态的概率分布即为当前状态抵达其他所有其他状态的概率分布。
其数学表达式为: P ( x t + 1 ∣ … x t − 2 , x t − 1 , x t ) = P ( x t + 1 ∣ x t ) P(x_{t+1}|\ldots x_{t-2},x_{t-1},x_{t})=P(x_{t+1}|x_t) P(xt+1∣…xt−2,xt−1,xt)=P(xt+1∣xt);
因此只要知道HMM模型中任意两个隐藏状态之间的转移概率,就可以得到该模型的状态转移矩阵。
HMM模型
如上述所说,HMM模型包含隐藏状态和观测状态,观测状态与隐藏状态之间存在联系,模型中的参数用来表示这中联系。下面用不同面数的骰子的例子形象解释这一模型。
三个不同的骰子(六个面的D6、四个面的D4、八个面的D8)就表示三种隐藏状态,每个骰子可以摇出来的数字就是不同的观测状态。
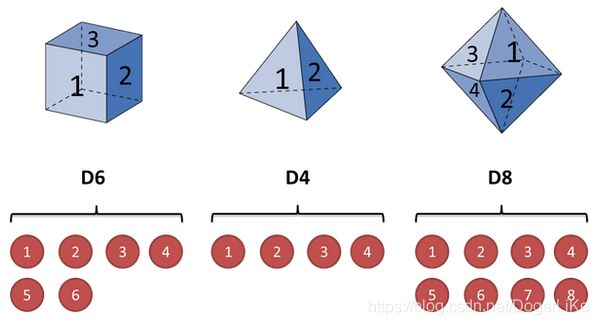
假设我们每次掷骰子掷出三个骰子的概率相同,每一个骰子可能掷出的数字出现概率相等,那么每个骰子转移为其它骰子的概率分布均为 ( 1 3 , 1 3 , 1 3 ) ({1\over 3},{1\over 3},{1\over 3}) (31,31,31),并且初始状态概率也为 ( 1 3 , 1 3 , 1 3 ) ({1\over 3},{1\over 3},{1\over 3}) (31,31,31),ps:初始状态概率与状态转移概率无关。
我们开始掷骰子之后便能够获得一串数字,假设投掷五次,得到的数字依次排列为:1、6、3、7、2,这组数字就是我们的观测状态序列。
目前我们已知了各个骰子之间的转移概率(隐藏状态的转移概率)、每个骰子掷出不同数字的概率(隐藏状态与观测状态的对应信息)、第一次掷出各个骰子的概率(初始概率)、投掷五次出现的数字序列(观测状态序列)。那么如果我们想要知道投掷五次骰子,每次投掷出来的骰子分别时哪种骰子,这种问题就是隐马尔可夫模型的观测问题。
求解隐马尔可夫模型观测问题便要用到维比特算法(Viterbi Algorithm)。
维特比算法
维特比算法是从初始状态开始,根据观测状态序列计算这一情况下依次排列每种隐藏状态的概率。
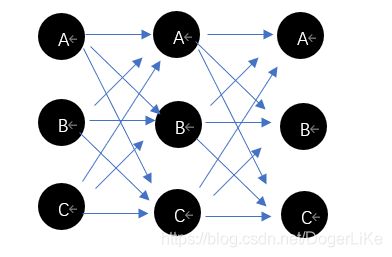
图中A、B、C均代表隐藏状态,维比特算法也就是计算途中每条状态转移链路得出观测状态序列的概率,选择最出现概率最大的一条作为预测结果。
下面将用一个故事来提供预测问题的应用场景,并在后文中给出解决这一问题的不同语言的算法实现。
小蝌蚪找妈妈
池塘里有一群小蝌蚪,大大的脑袋,黑灰色的身子,甩着长长的尾巴,快活地游来游去。小蝌蚪游哇游,过了几天,长出两条后腿。它们看见鲤鱼妈妈在教小鲤鱼捕食,就迎上去,问:“鲤鱼阿姨,鲤鱼阿姨,你知道我们的妈妈在哪里嘛?”
鲤鱼妈妈说:“我不知道你们的妈妈在哪里,但是你们的妈妈和我说,她未来三天会在池塘、河边、河岸出现,但不一定这些地方全都去,而且你们的妈妈决定未来三天的日程安排是:休息、捕食、捕食,你们自己碰一碰运气吧!”
小蝌蚪们听完蛙都傻了,迷迷糊糊地游着,突然撞上了乌龟爷爷,乌龟爷爷听了他们的叙述,微微一笑,说:“让我们用隐马尔可夫模型和维特比算法预测一下吧!”
乌龟爷爷告诉了小蝌蚪们经过自己多年来的观察,青蛙妈妈的习惯是这样子的:
| 上一个地方 \ 下一个地方 | 池塘 | 河边 | 河岸 |
|---|---|---|---|
| 池塘 | 0.7 | 0.2 | 0.1 |
| 河边 | 0.3 | 0.3 | 0.4 |
| 河岸 | 0.3 | 0.5 | 0.2 |
乌龟爷爷说:"稍微对这个表格做些说明,比如第一行,前一天去了池塘后,第二天还待在池塘的概率为0.7,去河边的概率为0.2,去河岸的概率为0.1。”
| 地点 \ 行为 | 休息 | 捕食 |
|---|---|---|
| 池塘 | 0.9 | 0.1 |
| 河边 | 0.5 | 0.5 |
| 河岸 | 0.2 | 0.8 |
乌龟爷爷说:“这是你们妈妈在不同地方做不同事情的概率。”
小蝌蚪问:“那第一天妈妈会在哪里呢?”
乌龟爷爷说:“傻孩子们,你们妈妈第一天在那个地方都有可能啊,每个地方都一样啦。”
那么,怎么才能帮助小蝌蚪们预测出来青蛙妈妈未来三天出现在哪里呢?
Matlab实现
乌龟爷爷问小蝌蚪们,“我这里有两种方法,一个简单一个复杂,你们想用哪种方法呀?”
小蝌蚪们喊道:“简单的!”
TRANS = [0.7 0.2 0.1;
0.3 0.3 0.4;
0.3 0.5 0.2];%转移矩阵A
EMIS = [0.9, 0.1;
0.5, 0.5;
0.2, 0.8];%混淆矩阵B
seq=[1 2 2]; %观测状态序列
likelystates = hmmviterbi(seq, TRANS, EMIS);
Python实现
乌龟爷爷说完简单方法后说:“现在简单的方法不能随便用啦,有深海鱼把我们浅水生物归为禁用名单啦,你们年轻人得学一学其他方法”
小蝌蚪们:“wdnmd深海鱼!”
# -*- coding: utf-8 -*-
# HMM.py
# Using Vertibi algorithm
import numpy as np
def Viterbi(A, B, PI, V, Q, obs):
N = len(Q)
T = len(obs)
#最大转移概率
delta = np.array([[0] * N] * T, dtype=np.float64)
#最大转移概率来源
phi = np.array([[0] * N] * T, dtype=np.int64)
# 初始化
for i in range(N):
delta[0, i] = PI[i]*B[i][V.index(obs[0])]
phi[0, i] = 0
# 递归计算
for i in range(1, T):
for j in range(N):
tmp = [delta[i-1, k]*A[k][j] for k in range(N)]#计算每一隐藏状态转移到某一状态的概率
delta[i,j] = max(tmp) * B[j][V.index(obs[i])]#计算转移后表现观测概率的概率
phi[i,j] = tmp.index(max(tmp))#转移前上一隐藏状态
# 最终的概率及节点
P = max(delta[T-1, :])
I = int(np.argmax(delta[T-1, :]))#返回一列内最大值的次序
# 最优路径path
path = [I]
for i in reversed(range(1, T)):
end = path[-1]#取倒数第一个
path.append(phi[i, end])#在最后添加
hidden_states = [Q[i] for i in reversed(path)]#倒叙输出
return P, hidden_states
def main():
# 状态集合
Q = ('池塘', '河边', '河岸')
# 观测集合
V = ['休息', '捕食']
# 转移概率: Q -> Q
A = [[0.7, 0.2, 0.1],
[0.3, 0.3, 0.4],
[0.3, 0.5, 0.2]
]
# 发射概率, Q -> V
B = [[0.9, 0.1],
[0.5, 0.5],
[0.8, 0.8]
]
# 初始概率
PI = [1/3, 1/3, 1/3]
# 观测序列
obs = ['休息', '捕食', '捕食']
P, hidden_states = Viterbi(A,B,PI,V,Q,obs)
print('最大的概率为: %.5f.'%P)
print('隐藏序列为:%s.'%hidden_states)
main()
所以你跑出来青蛙妈妈未来三天在哪里了嘛?
特别鸣谢
记录了学习和使用HMM模型和维比特算法解决预测问题的过程,带着自己的理解分享给大家。后续将会补充C++的代码实现。
在此特别鸣谢学习过程中借鉴的博客及博主!
链接: 一文搞懂HMM.
链接: 隐马尔可夫模型(HMM)及Viterbi算法.
链接: 马尔可夫链介绍.