VINS_MONO系列：(三)VIO初始化

目录

1、整体流程

2、理论推导

2.1、陀螺仪偏置标定

2.2、速度、重力及尺度初始化

2.3、重力优化

3、代码实现

4、探讨与思考

5、参考文献

---

相关链接：

 VINS_MONO系列：(一)总体框架_Derrr...的博客-CSDN博客_vins框架

VINS_MONO系列：(二)IMU预积分详细推导_Derrr...的博客-CSDN博客

VINS_MONO系列：(三)VIO初始化_Derrr...的博客-CSDN博客

VINS_MONO系列：(四)紧耦合VIO实现_Derrr...的博客-CSDN博客

 VINS_MONO系列：(五)前端特征提取_Derrr...的博客-CSDN博客

1、整体流程

VINS中的初始化采用了松耦合的方案，将陀螺仪偏置、速度、重力、尺度等状态量分别进行初始化，其主要包括三个步骤，分别是陀螺仪偏置的标定（Gyroscope Bias Calibration）、速度、重力及尺度的初始化（Velocity, Gravity Vector and Metric Scale Initialization）以及重力优化（Gravity Refinement）等等，其整体的流程也按照这个顺序进行的。

2、理论推导

2.1、陀螺仪偏置标定

陀螺仪偏置标定的主要思想是借助纯视觉的sfm作为真值，对陀螺仪偏置进行标定。虽然纯单目的初始化会存在尺度不确定性的问题，但是角度的估计是准确的，因此可以将关键帧的角度值作为观测量构建优化问题：

理论上该优化问题的最优值为，因此联立后可以改写为

只考虑虚部，则有

 

随后进行cholesky分解后即可获得陀螺仪偏置的误差项

2.2、速度、重力及尺度初始化

这部分主要是通过IMU的预积分值对视觉sfm的速度、重力及尺度进行初始化，优化变量为

考虑连续两帧关键帧的P和V的变化量，有

 

根据

将上式代入上上式，有

将上式写成矩阵相乘形式，则有

其中

最后优化问题可以写为：

最后通过高斯牛顿法可以求解出状态向量。

2.3、重力优化

以上步骤完以后，理论上已经完成各个状态量的初始化了，但在2.2中求解重力向量时，没有把重力的内在约束考虑进行，因此最后需要加入重力向量内部的约束后再进行一次优化。

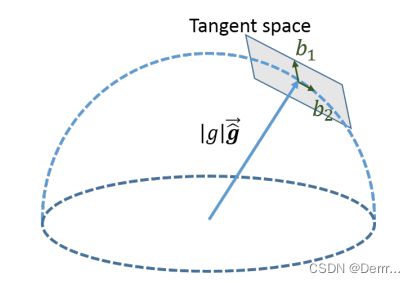
我们知道重力的绝对值一般为9.8m/s2，因此可以仅用两个变量对重力向量进行参数化：

其中为与重力垂直的两个向量，如图1所示，可以通过如图2的算法获得。

图1

        图2

因此优化变量可以改写为

将式(15)代入式(8)和式(12)，并将其写成矩阵形式则有

其中

 

至此，VIO初始化部分的理论推导完毕。

3、代码实现

初始化部分的代码主要包括在Estimator::initialStructure()函数中，其中的内容包括纯视觉的sfm求解、陀螺仪偏置计算、重力、速度及尺度值计算和重力优化等几个方面，其主要流程及对应的函数实现如图3所示。

图3

• 纯视觉SFM

relativePose

该函数主要功能是遍历滑窗中的所有图像帧，找到与当前帧具有足够时差与特征点的帧作为初始帧，并计算当前帧到初始帧的R和t，最后返回初始帧的index l，当前帧相对初始帧的旋转relative_R和平移relative_T

bool Estimator::relativePose(Matrix3d &relative_R, Vector3d &relative_T, int &l)
{
    for (int i = 0; i < WINDOW_SIZE; i++)
    {
        vector> corres;
        corres = f_manager.getCorresponding(i, WINDOW_SIZE); //获取当前帧与第i帧的共视特征点
        if (corres.size() > 20)
        {
            double sum_parallax = 0;
            double average_parallax;
            for (int j = 0; j < int(corres.size()); j++)
            {
                Vector2d pts_0(corres[j].first(0), corres[j].first(1));
                Vector2d pts_1(corres[j].second(0), corres[j].second(1));
                double parallax = (pts_0 - pts_1).norm();
                sum_parallax = sum_parallax + parallax;

            }
            average_parallax = 1.0 * sum_parallax / int(corres.size());
            if(average_parallax * 460 > 30 && m_estimator.solveRelativeRT(corres, relative_R, relative_T))  //通过cv::findFundamentalMat计算本质矩阵，并结算R、t
            {
                l = i;
                ROS_DEBUG("average_parallax %f choose l %d and newest frame to triangulate the whole structure", average_parallax * 460, l);
                return true;
            }
        }
    }
    return false;
}

construct

这个函数实现整个纯视觉SFM，包括solveFrameByPnP求解各帧位姿、triangulateTwoFrames三角化两帧间的特征点，再在最后进行fullBA，优化整个SFM的结果。

bool GlobalSFM::construct(int frame_num, Quaterniond* q, Vector3d* T, int l,
			  const Matrix3d relative_R, const Vector3d relative_T,
			  vector &sfm_f, map &sfm_tracked_points)
{
	/*省略*/

	//1: trangulate between l ----- frame_num - 1
	//2: solve pnp l + 1; trangulate l + 1 ------- frame_num - 1; 
	for (int i = l; i < frame_num - 1 ; i++)
	{
		// solve pnp
		if (i > l)
		{
			Matrix3d R_initial = c_Rotation[i - 1];
			Vector3d P_initial = c_Translation[i - 1];
			if(!solveFrameByPnP(R_initial, P_initial, i, sfm_f))
				return false;
			c_Rotation[i] = R_initial;
			c_Translation[i] = P_initial;
			c_Quat[i] = c_Rotation[i];
			Pose[i].block<3, 3>(0, 0) = c_Rotation[i];
			Pose[i].block<3, 1>(0, 3) = c_Translation[i];
		}

		// triangulate point based on the solve pnp result
		triangulateTwoFrames(i, Pose[i], frame_num - 1, Pose[frame_num - 1], sfm_f);
	}
	//3: triangulate l-----l+1 l+2 ... frame_num -2
	for (int i = l + 1; i < frame_num - 1; i++)
		triangulateTwoFrames(l, Pose[l], i, Pose[i], sfm_f);
	//4: solve pnp l-1; triangulate l-1 ----- l
	//             l-2              l-2 ----- l
	for (int i = l - 1; i >= 0; i--)
	{
		//solve pnp
		Matrix3d R_initial = c_Rotation[i + 1];
		Vector3d P_initial = c_Translation[i + 1];
		if(!solveFrameByPnP(R_initial, P_initial, i, sfm_f))
			return false;
		c_Rotation[i] = R_initial;
		c_Translation[i] = P_initial;
		c_Quat[i] = c_Rotation[i];
		Pose[i].block<3, 3>(0, 0) = c_Rotation[i];
		Pose[i].block<3, 1>(0, 3) = c_Translation[i];
		//triangulate
		triangulateTwoFrames(i, Pose[i], l, Pose[l], sfm_f);
	}
	//5: triangulate all other points
	for (int j = 0; j < feature_num; j++)
	{
		if (sfm_f[j].state == true)
			continue;
		if ((int)sfm_f[j].observation.size() >= 2)
		{
			Vector2d point0, point1;
			int frame_0 = sfm_f[j].observation[0].first;
			point0 = sfm_f[j].observation[0].second;
			int frame_1 = sfm_f[j].observation.back().first;
			point1 = sfm_f[j].observation.back().second;
			Vector3d point_3d;
			triangulatePoint(Pose[frame_0], Pose[frame_1], point0, point1, point_3d);
			sfm_f[j].state = true;
			sfm_f[j].position[0] = point_3d(0);
			sfm_f[j].position[1] = point_3d(1);
			sfm_f[j].position[2] = point_3d(2);
		}		
	}

	//full BA
	ceres::Problem problem;
	ceres::LocalParameterization* local_parameterization = new ceres::QuaternionParameterization();
	//cout << " begin full BA " << endl;
	for (int i = 0; i < frame_num; i++)
	{
		//double array for ceres
		c_translation[i][0] = c_Translation[i].x();
		c_translation[i][1] = c_Translation[i].y();
		c_translation[i][2] = c_Translation[i].z();
		c_rotation[i][0] = c_Quat[i].w();
		c_rotation[i][1] = c_Quat[i].x();
		c_rotation[i][2] = c_Quat[i].y();
		c_rotation[i][3] = c_Quat[i].z();
		problem.AddParameterBlock(c_rotation[i], 4, local_parameterization);
		problem.AddParameterBlock(c_translation[i], 3);
		if (i == l)
		{
			problem.SetParameterBlockConstant(c_rotation[i]);
		}
		if (i == l || i == frame_num - 1)
		{
			problem.SetParameterBlockConstant(c_translation[i]);
		}
	}

	for (int i = 0; i < feature_num; i++)
	{
		if (sfm_f[i].state != true)
			continue;
		for (int j = 0; j < int(sfm_f[i].observation.size()); j++)
		{
			int l = sfm_f[i].observation[j].first;
			ceres::CostFunction* cost_function = ReprojectionError3D::Create(
												sfm_f[i].observation[j].second.x(),
												sfm_f[i].observation[j].second.y());

    		problem.AddResidualBlock(cost_function, NULL, c_rotation[l], c_translation[l], 
    								sfm_f[i].position);	 
		}

	}
	ceres::Solver::Options options;
	options.linear_solver_type = ceres::DENSE_SCHUR;
	//options.minimizer_progress_to_stdout = true;
	options.max_solver_time_in_seconds = 0.2;
	ceres::Solver::Summary summary;
	ceres::Solve(options, &problem, &summary);
	//std::cout << summary.BriefReport() << "\n";
	if (summary.termination_type == ceres::CONVERGENCE || summary.final_cost < 5e-03)
	{
		//cout << "vision only BA converge" << endl;
	}
	else
	{
		//cout << "vision only BA not converge " << endl;
		return false;
	}
	for (int i = 0; i < frame_num; i++)
	{
		q[i].w() = c_rotation[i][0]; 
		q[i].x() = c_rotation[i][1]; 
		q[i].y() = c_rotation[i][2]; 
		q[i].z() = c_rotation[i][3]; 
		q[i] = q[i].inverse();
		//cout << "final  q" << " i " << i <<"  " <

• 陀螺仪偏置计算

solveGyroscopeBias

计算各帧的陀螺仪偏置，最后再基于新的陀螺仪偏置重新计算各帧预积分值。

void solveGyroscopeBias(map &all_image_frame, Vector3d* Bgs)
{
    Matrix3d A;
    Vector3d b;
    Vector3d delta_bg;
    A.setZero();
    b.setZero();
    map::iterator frame_i;
    map::iterator frame_j;
    for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++)
    {
        frame_j = next(frame_i);
        MatrixXd tmp_A(3, 3);
        tmp_A.setZero();
        VectorXd tmp_b(3);
        tmp_b.setZero();
        Eigen::Quaterniond q_ij(frame_i->second.R.transpose() * frame_j->second.R);
        tmp_A = frame_j->second.pre_integration->jacobian.template block<3, 3>(O_R, O_BG); // 对应公式(6)中的Jbg
        tmp_b = 2 * (frame_j->second.pre_integration->delta_q.inverse() * q_ij).vec();
        A += tmp_A.transpose() * tmp_A; //对应公式(6)中等号左侧部分
        b += tmp_A.transpose() * tmp_b;  //对应公式(6)中等号右侧部分

    }
    // 利用Cholosky 分解计算，这里求解出来的结果为陀螺仪偏置的误差
    delta_bg = A.ldlt().solve(b);
    ROS_WARN_STREAM("gyroscope bias initial calibration " << delta_bg.transpose());

    std::cout << "bg after optimization: " << delta_bg.transpose()<< std::endl;
    for (int i = 0; i <= WINDOW_SIZE; i++)
    {
        Bgs[i] += delta_bg;
    }

    for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end( ); frame_i++)
    {
        frame_j = next(frame_i);
        frame_j->second.pre_integration->repropagate(Vector3d::Zero(), Bgs[0]);
    }
}

• 重力、速度、尺度计算

LinearAlignment

bool LinearAlignment(map &all_image_frame, Vector3d &g, VectorXd &x)
{
    int all_frame_count = all_image_frame.size();
    int n_state = all_frame_count * 3 + 3 + 1; //总共优化变量的维度

    MatrixXd A{n_state, n_state};
    A.setZero();
    VectorXd b{n_state};
    b.setZero();

    map::iterator frame_i;
    map::iterator frame_j;
    int i = 0;
    for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
    {
        frame_j = next(frame_i);

        MatrixXd tmp_A(6, 10);
        tmp_A.setZero();
        VectorXd tmp_b(6);
        tmp_b.setZero();

        double dt = frame_j->second.pre_integration->sum_dt;
        // tmp_A对应公式(13)中的H矩阵
        tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
        tmp_A.block<3, 3>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity();
        tmp_A.block<3, 1>(0, 9) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;     
        // tmp_b对应公式(13)中的z矩阵
        tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0];
        tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
        tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
        tmp_A.block<3, 3>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity();
        tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v;

        Matrix cov_inv = Matrix::Zero();

        cov_inv.setIdentity();

        MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
        VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
        // 把r_A，r_b分别放入大矩阵A和b的对应的位置
        A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
        b.segment<6>(i * 3) += r_b.head<6>();

        A.bottomRightCorner<4, 4>() += r_A.bottomRightCorner<4, 4>();
        b.tail<4>() += r_b.tail<4>();

        A.block<6, 4>(i * 3, n_state - 4) += r_A.topRightCorner<6, 4>();
        A.block<4, 6>(n_state - 4, i * 3) += r_A.bottomLeftCorner<4, 6>();
    }
    // 保证数值稳定性
    A = A * 1000.0;
    b = b * 1000.0;

    // 利用Cholosky 分解计算
    x = A.ldlt().solve(b);
    double s = x(n_state - 1) / 100.0;
    ROS_DEBUG("estimated scale: %f", s);
    std::cout << "g befor optimization: " << g.transpose() << std::endl;
    g = x.segment<3>(n_state - 4);
    std::cout << "g after optimization: " << g.transpose() << std::endl;
    ROS_DEBUG_STREAM(" result g     " << g.norm() << " " << g.transpose());
    if(fabs(g.norm() - G.norm()) > 1.0 || s < 0)
    {
        return false;
    }
    // 重力优化
    RefineGravity(all_image_frame, g, x);
    std::cout << "g after refine: " << g.transpose() << std::endl;

    s = (x.tail<1>())(0) / 100.0;
    (x.tail<1>())(0) = s;
    ROS_DEBUG_STREAM(" refine     " << g.norm() << " " << g.transpose());
    if(s < 0.0 )
        return false;   
    else
        return true;
}

• 重力优化

RefineGravity

void RefineGravity(map &all_image_frame, Vector3d &g, VectorXd &x)
{
    Vector3d g0 = g.normalized() * G.norm();
    Vector3d lx, ly;
    //VectorXd x;
    int all_frame_count = all_image_frame.size();
    int n_state = all_frame_count * 3 + 2 + 1; //总共优化变量的维度

    MatrixXd A{n_state, n_state};
    A.setZero();
    VectorXd b{n_state};
    b.setZero();

    map::iterator frame_i;
    map::iterator frame_j;
    for(int k = 0; k < 4; k++) //迭代优化四次
    {
        MatrixXd lxly(3, 2);
        lxly = TangentBasis(g0);
        int i = 0;
        for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
        {
            frame_j = next(frame_i);

            MatrixXd tmp_A(6, 9);
            tmp_A.setZero();
            VectorXd tmp_b(6);
            tmp_b.setZero();

            double dt = frame_j->second.pre_integration->sum_dt;

            // tmp_A对应公式(16)中的H矩阵
            tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
            tmp_A.block<3, 2>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity() * lxly;
            tmp_A.block<3, 1>(0, 8) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;     
            // tmp_b对应公式(16)中的z矩阵
            tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0] - frame_i->second.R.transpose() * dt * dt / 2 * g0;

            tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
            tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
            tmp_A.block<3, 2>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity() * lxly;
            tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v - frame_i->second.R.transpose() * dt * Matrix3d::Identity() * g0;


            Matrix cov_inv = Matrix::Zero();
            cov_inv.setIdentity();

            MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
            VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
            // 填充大矩阵
            A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
            b.segment<6>(i * 3) += r_b.head<6>();

            A.bottomRightCorner<3, 3>() += r_A.bottomRightCorner<3, 3>();
            b.tail<3>() += r_b.tail<3>();

            A.block<6, 3>(i * 3, n_state - 3) += r_A.topRightCorner<6, 3>();
            A.block<3, 6>(n_state - 3, i * 3) += r_A.bottomLeftCorner<3, 6>();
        }
            // 保证数值稳定
            A = A * 1000.0;
            b = b * 1000.0;
            // 利用Cholosky 分解计算
            x = A.ldlt().solve(b);
            VectorXd dg = x.segment<2>(n_state - 3);
            // 更新重力结果
            g0 = (g0 + lxly * dg).normalized() * G.norm();
            //double s = x(n_state - 1);
    }   
    g = g0;
}

4、探讨与思考

• 加速度计偏置

VINS中初始化部分缺少对于加速度计偏置的初始化，这不可避免的在精度有会有一定的损失，但其实加速度计的偏置也是可以进行估计的，具体可以查看ORBSLAM3中的实现[2]，个人感觉ORB中的初始化在理论上更完备一点。

• 重力向量

重力向量的估计是非常重要的，它主要是提供初始帧相对于世界坐标系的transform。但是，重力向量的值通常是与加速度计偏置和当时瞬时的加速度值耦合在一起的，需要从加速度中分解出其中正真的重力分量。

• 尺度的计算

在代码实现中，尺度s在优化完之后需要再除以100，不清楚这个操作具体是有什么用意？

• 滑窗中的偏置

从陀螺仪偏置的代码实现中可以看到，初始化时滑窗中所有帧的陀螺仪偏置都是一样的。不仅如此，实际上在完成初始化后，在紧耦合VIO的求解中，每次滑窗中的加速度计偏置和陀螺仪偏置都是一样的，这主要是因为损失函数的设计导致的。

5、参考文献

[1] Tong Q ,  Li P ,  Shen S . VINS-Mono[J]. IEEE Transactions on Robotics, 2018.

[2] Mur-Artal R ,  Tardos J D . Visual-Inertial Monocular SLAM with Map Reuse[J]. IEEE Robotics and Automation Letters, 2016, PP(99):796-803.