二叉树中的那些常见的面试题

树 二叉树 森林之间的相互转换详见: http://student.zjzk.cn/course_ware/data_structure/web/shu/shu6.5.1.htm

二叉树作为树的一种，是一种重要的数据结构，也是面试官经常考的东西。昨天看了一下关于树中的面试题，发现二叉树中的面试题比较常见的题型大概有下面几个：创建一颗二叉树（先序，中序，后序）、遍历一颗二叉树（先序，中序，后序和层次遍历）、求二叉树中叶子节点的个数、求二叉树的高度、求二叉树中两个节点的最近公共祖先、打印和为某一值的全部路径、求某一节点是否在一个树中等等。

再详细的说这些面试题之前，不妨先看一下几种常见的二叉树：

完全二叉树：若二叉树的高度是h，除第h层之外，其他（1~h-1）层的节点数都达到了最大个数，并且第h层的节点都连续的集中在最左边。想到点什么没？实际上，完全二叉树和堆联系比较紧密哈~~~

满二叉树：除最后一层外，每一层上的所有节点都有两个子节点，最后一层都是叶子节点。

哈夫曼树：又称为最有数，这是一种带权路径长度最短的树。哈夫曼编码就是哈夫曼树的应用。

平衡二叉树：所谓平衡二叉树指的是，左右两个子树的高度差的绝对值不超过 1。

红黑树：红黑树是每个节点都带颜色的树，节点颜色或是红色或是黑色，红黑树是一种查找树。红黑树有一个重要的性质，从根节点到叶子节点的最长的路径不多于最短的路径的长度的两倍。对于红黑树，插入，删除，查找的复杂度都是O（log N）。

二叉树中的那些面试题

---

 

1 创建一颗二叉树

创建一颗二叉树，可以创建先序二叉树，中序二叉树，后序二叉树。我们在创建的时候为了方便，不妨用‘#’表示空节点，这时如果先序序列是：6 4 2 3 # # # # 5 1 # # 7 # #，那么创建的二叉树如下：

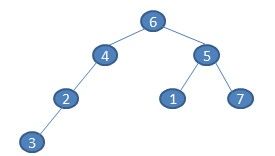
下面是创建二叉树的完整代码：创建一颗二叉树，返回二叉树的根。

 

1 //创建二叉树，这里不妨使用前序创建二叉树，遇到‘#’表示节点为空  2 BinTreeNode* BinTree::create_tree()  3 {  4 char item;  5 BinTreeNode *t,*t_l,*t_r;  6 cin>>item;  7 if(item != '#')  8  {  9 BinTreeNode *pTmpNode = new BinTreeNode(item-48); 10 t = pTmpNode; 11 t_l = create_tree(); 12 t->set_left(t_l); 13 t_r = create_tree(); 14 t->set_right(t_r); 15 return t; 16  } 17 else 18  { 19 t = NULL; 20 return t; 21  } 22 } 

2.层次遍历

层次遍历也是二叉树遍历的一种方式，二叉树的层次遍历更像是一种广度优先搜索（BFS）。因此二叉树的层次遍历利用队列来完成是最好不过啦，当然不是说利用别的数据结构不能完成。

 

1 //层次遍历  2 void BinTree::level_order(BinTreeNode *r)const  3 {  4 if(r == NULL)  5 return;  6 deque q;  7  q.push_back(r);  8 while(!q.empty())  9  { 10 BinTreeNode *pTmpNode = q.front(); 11 cout<<pTmpNode->get_data()<<" "; 12  q.pop_front(); 13 if(pTmpNode->get_left() != NULL) 14  { 15 q.push_back(pTmpNode->get_left()); 16  } 17 if(pTmpNode->get_right() != NULL) 18  { 19 q.push_back(pTmpNode->get_right()); 20  } 21  } 22 } 

 

3.求二叉树中叶子节点的个数

树中的叶子节点的个数 = 左子树中叶子节点的个数 + 右子树中叶子节点的个数。利用递归代码也是相当的简单，易懂。

 

1 //获取叶子节点的个数  2 int BinTree::get_leaf_num(BinTreeNode *r)const  3 {  4 if(r == NULL)//该节点是空节点，比如建树时候用'#'表示  5  {  6 return 0;  7  }  8 if(r->get_left()==NULL && r->get_right()==NULL)//该节点并不是空的，但是没有孩子节点  9  { 10 return 1; 11  } 12 //递归整个树的叶子节点个数 = 左子树叶子节点的个数 + 右子树叶子节点的个数 13 return get_leaf_num(r->get_left()) + get_leaf_num(r->get_right()); 14 } 

 

4.求二叉树的高度

求二叉树的高度也是非常简单，不用多说：树的高度 = max(左子树的高度，右子树的高度) + 1 

 

1 //获得二叉树的高度  2 int BinTree::get_tree_height(BinTreeNode *r)const  3 {  4 if(r == NULL)//节点本身为空  5  {  6 return 0;  7  }  8 if(r->get_left()==NULL && r->get_right()==NULL)//叶子节点  9  { 10 return 1; 11  } 12 int l_height = get_tree_height(r->get_left()); 13 int r_height = get_tree_height(r->get_right()); 14 return l_height >= r_height ? l_height + 1 : r_height + 1; 15 } 

 

5.交换二叉树的左右儿子

交换二叉树的左右儿子，可以先交换根节点的左右儿子节点，然后递归以左右儿子节点为根节点继续进行交换。

 

1 //交换二叉树的左右儿子  2 void BinTree::swap_left_right(BinTreeNode *r)  3 {  4 if(r == NULL)  5  {  6 return;  7  }  8 BinTreeNode *pTmpNode = r->get_left();  9 r->set_left(r->get_right()); 10 r->set_right(pTmpNode); 11 swap_left_right(r->get_left()); 12 swap_left_right(r->get_right()); 13 } 

6.判断一个节点是否在一颗子树中

可以和当前根节点相等，也可以在左子树或者右子树中。 

 

1 //判断一个节点t是否在以r为根的子树中  2 bool BinTree::is_in_tree(BinTreeNode *r,BinTreeNode *t)const  3 {  4 if(r == NULL)  5  {  6 return false;  7  }  8 else if(r == t)  9  { 10 return true; 11  } 12 else 13  { 14 bool has = false; 15 if(r->get_left() != NULL) 16  { 17 has = is_in_tree(r->get_left(),t); 18  } 19 if(!has && r->get_right()!= NULL) 20  { 21 has = is_in_tree(r->get_right(),t); 22  } 23 return has; 24  } 25 } 

 

7.求两个节点的最近公共祖先

求两个节点的公共祖先可以用到上面的：判断一个节点是否在一颗子树中。（1）如果两个节点同时在根节点的右子树中，则最近公共祖先一定在根节点的右子树中。（2）如果两个节点同时在根节点的左子树中，则最近公共祖先一定在根节点的左子树中。（3）如果两个节点一个在根节点的右子树中，一个在根节点的左子树中，则最近公共祖先一定是根节点。当然，要注意的是：可能一个节点pNode1在以另一个节点pNode2为根的子树中，这时pNode2就是这两个节点的最近公共祖先了。显然这也是一个递归的过程啦：

 

1 //求两个节点的最近公共祖先  2 BinTreeNode* BinTree::get_nearest_common_father(BinTreeNode *r,BinTreeNode *pNode1,BinTreeNode *pNode2)const  3 {  4 //pNode2在以pNode1为根的子树中（每次递归都要判断，放在这里不是很好。）  5 if(is_in_tree(pNode1,pNode2))  6  {  7 return pNode1;  8  }  9 //pNode1在以pNode2为根的子树中 10 if(is_in_tree(pNode2,pNode1)) 11  { 12 return pNode2; 13  } 14 bool one_in_left,one_in_right,another_in_left,another_in_right; 15 one_in_left = is_in_tree(r->get_left(),pNode1); 16 another_in_right = is_in_tree(r->get_right(),pNode2); 17 another_in_left = is_in_tree(r->get_left(),pNode2); 18 one_in_right = is_in_tree(r->get_right(),pNode1); 19 if((one_in_left && another_in_right) || (one_in_right && another_in_left)) 20  { 21 return r; 22  } 23 else if(one_in_left && another_in_left) 24  { 25 return get_nearest_common_father(r->get_left(),pNode1,pNode2); 26  } 27 else if(one_in_right && another_in_right) 28  { 29 return get_nearest_common_father(r->get_right(),pNode1,pNode2); 30  } 31 else 32  { 33 return NULL; 34  } 35 } 

8.从根节点开始找到所有路径，使得路径上的节点值和为某一数值（路径不一定以叶子节点结束）

这道题要找到所有的路径，显然是用深度优先搜索（DFS）啦。但是我们发现DFS所用的栈和输出路径所用的栈应该不是一个栈，栈中的数据是相反的。看看代码：注意使用的两个栈。

 

1 //注意这两个栈的使用  2 stackdfs_s;  3 stackprint_s;  4 //打印出从r开始的和为sum的所有路径  5 void BinTree::print_rout(BinTreeNode *r,int sum)const  6 {  7 if(r == NULL)  8  {  9 return; 10  } 11 //入栈 12 sum -= r->get_data(); 13  dfs_s.push(r); 14 if(sum <= 0) 15  { 16 if(sum == 0) 17  { 18 while(!dfs_s.empty()) 19  { 20  print_s.push(dfs_s.top()); 21  dfs_s.pop(); 22  } 23 while(!print_s.empty()) 24  { 25 cout<<print_s.top()->get_data()<<" "; 26  dfs_s.push(print_s.top()); 27  print_s.pop(); 28  } 29 cout<<endl; 30  } 31 sum += r->get_data(); 32  dfs_s.pop(); 33 return; 34  } 35 //递归进入左子树 36 print_rout(r->get_left(),sum); 37 //递归进入右子树 38 print_rout(r->get_right(),sum); 39 //出栈 40 sum += r->get_data(); 41  dfs_s.pop(); 42 }