【数据结构】查找：顺序查找、折半查找、二叉排序树、平衡二叉树、B树、哈希查找
整理内容来源：zzu信息工程学院数据结构ppt
本节讨论两类不同的查找表：静态查找表和动态查找表，给出在不同查找表上进行查找的不同算法和性能分析以及动态查找表的创建方法。
1 查找的基本概念
静态查找：
- 基于线性表的查找
动态查找：
- 基于树的查找（二叉排序树、平衡二叉排序树、B-树和B+树）
- 基于散列表的查找
2 基于线性表的查找
2.1 定义和分类
基于线性表的查找主要是两部分：（索引顺序表用的不是很多）
- 顺序查找（适用于两种存储结构）
- 折半查找（有序表）
注意区分 “有序” 和 “顺序”：有序表中的“有序”是逻辑意义上的有序，指表中的元素按某种规则已经排好了位置。顺序表中的“顺序”是物理意义上的，指线形表中的元素一个接一个的存储在一片相邻的存储区域中。可以粗略地将“顺序表”理解为数组，将“有序表”理解为排好的数组。
2.2 顺序查找
2.2.1 思想
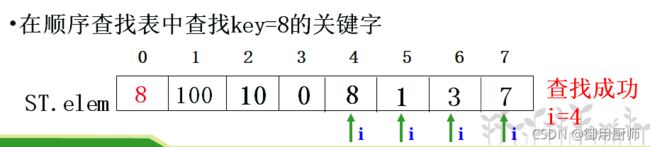
从表中第一条/最后一条记录开始，逐个进行记录的关键字与给定值的比较，若某个记录的关键字和给定值比较相等，则查找成功，返回其在顺序表中的位序；反之，若直至最后一条/第一条记录其关键字和给定值比较都不等，则查找不成功，返回0。
2.2.2 算法实现
监视哨：为能自动检验数组下标越界，在0下标处设置哨兵，若查找不成功，则循环会在0下标处自动终止，函数返回0。
int Search_Seq( SSTable ST, KeyType key ){
ST.elem[0].key = key; //0下标为监视哨
for(i = ST.length; !EQ(ST.elem[i].key,key ); --i);
return i;
}//Search_Seq
举例：
2.2.3 性能分析
这么暴力的做法时间复杂度当然不会低了
这里对O(n)可能没什么感觉，我们再往下看。
2.3 折半查找
折半查找在算法题中用的很多了，我之前专门写过关于折半查找的博客：算法 - 二分查找
2.3.1 定义
折半查找（二分查找）：先确定待查记录所在范围，逐步缩小范围，直到找到或找不到该记录止。
不过应注意，折半查找的应用范围是：有序表。
二分查找的思想和具体实现可参考那篇博客。
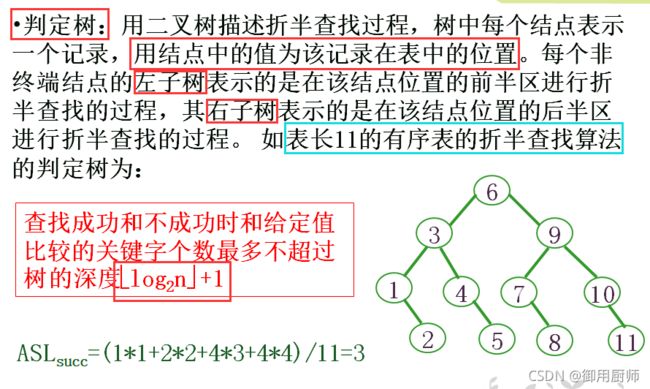
2.3.2 判定树
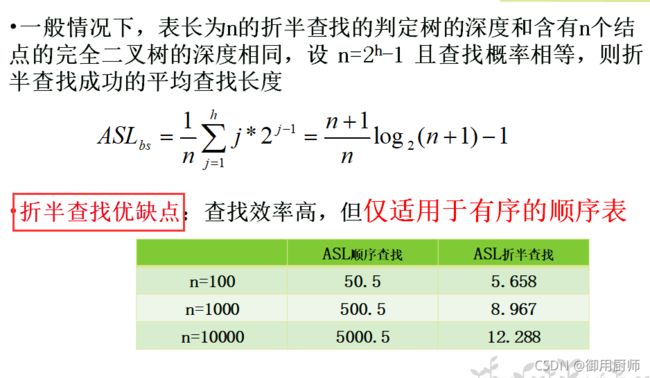
2.3.3 性能分析
时间复杂度为O(logn)，当数量级比较大时，时间复杂度的差异就体现出来了。详见下图：
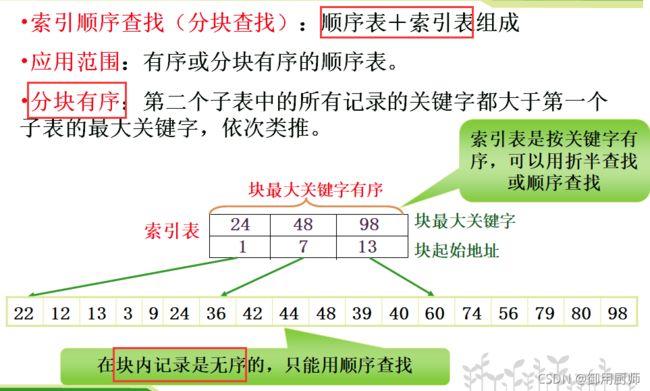
2.4 索引顺序表
索引顺序表就不展开讲了，它的特点是：分块有序、块内无序。
- 分块有序：用折半查找
- 块内无序：用顺序查找
3 二叉排序树（二叉查找树、BST）
3.1 定义
二叉排序树是指空树或具有下列性质的二叉树:（不得不感慨课件确实很严谨）
- 根的左子树若非空，则左子树上所有结点的关键字值均小于根结点的关键字值；
- 根的右子树若非空，则右子树上所有结点的关键字值均大于根结点的关键字值；
- 它的左右子树同样是二叉排序树。
可以看出，这是一种递归式定义。
3.2 查找过程
- 若二叉排序树为空，则查找失败，返回空指针；
- 若二叉排序树不空：
- 首先将给定值和根结点的关键字比较，若相等则查找成功，返回根结点的地址。
- 若给定值小于根结点的关键字值，则在其左子树上继续查找；
- 若给定值大于根结点的关键字值，则在其右子树上继续查找。
关于二叉排序树的算法实现，我们选用的存储结构是链式存储结构，即(lchild, data, rchild)。
原因是：链式存储结构可以快速实现插入和删除操作。
具体的算法如下：
BiTree SearchBST(BiTree T, KeyType key){
if((!T) || EQ(key,T->data.key)) return T;
if(LT(key,T->data.key))
return SearchBST(T->lchild, key);
else return SearchBST(T->rchild, key);
} //SearchBST
3.2 插入、构造方法
我们对查找算法可以适当修改，修改后的查找算法如下：
Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p){ //修改后的查找算法
if(!T){ p=f; return FALSE; }
else if EQ(key,T->data.key)
{ p=T; return TRUE; }
else if LT(key,T->data.key)
return SearchBST(T->lchild,key,T,p);
else return SearchBST(T->rchild,key,T,p);
}// SearchBST
其实对查找算法就是修改了如果查找不成功的话，对这个叶子结点进行了记录。（利用&p）
----------------------（乱入，前面的内容push一下）----------------
在这里突然想到了“指针和引用的区别”，之前看过一篇文章一直存着，分享给大家：指针与引用， 值传递与地址传递的关系
----------------------（前面的内容pop出来）---------------------------
如果得到了叶子结点，那我们就可以进行二叉排序树的插入操作了：
Status InsertBST(BiTree &T, ElemType e)
{
if(!SearchBST(T,e.key,NULL,p))
{
s=(BiTree)malloc(sizeof(BiTNode));
if(!s) exit(OVERFLOW);
s->data = e; s->lchild = s->rchild = NULL;
if(!p) T=s;
else if LT(e.key, p->data.key) p->lchild = s;
else p->rchild = s;
return TRUE;
}
else return FALSE;
}
插入的示例和补充：
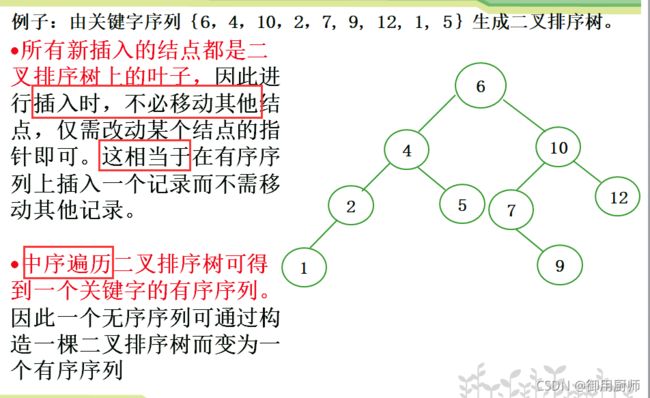
注意这里啊，在插入时，我们不需要移动其他结点，只需要修改一个结点的指针就好了。
并且我们还应注意到，BST的建树过程就是查找失败时元素不断插入的过程。
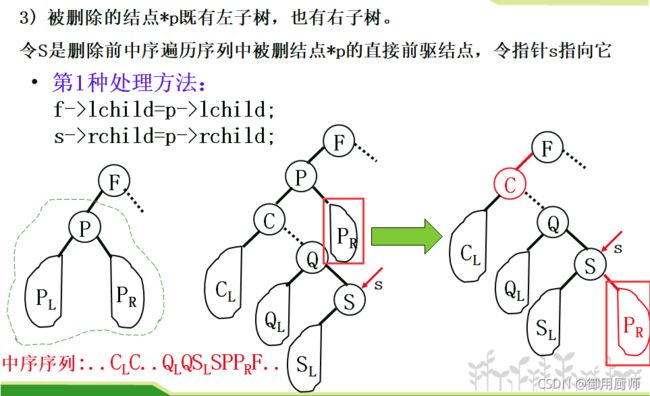
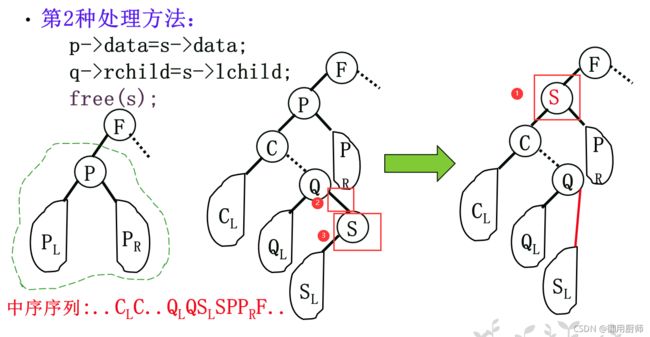
3.3 删除
对于一般的二叉树，删去树中的一个结点会破坏整棵树的结构。对二叉排序树，删去一个结点相当于删去有序序列中的一个记录。
在删除时，我们有以下几种情况：
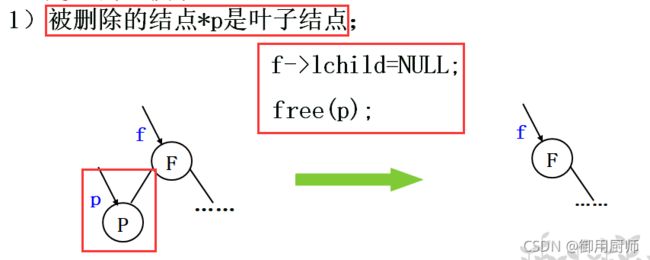
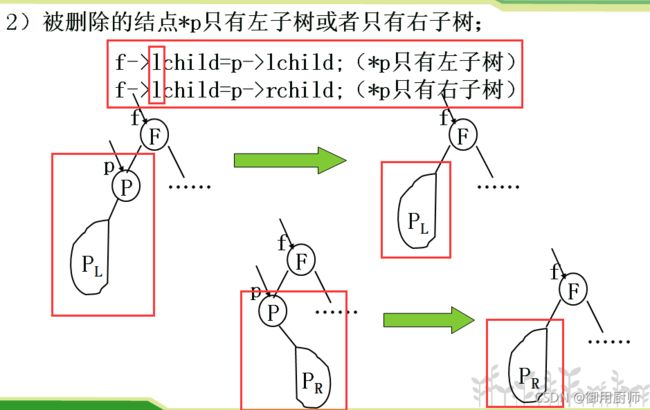
注意上面这种情况，不管被删结点是只有左子树还是只有右子树，都把它的某个子树挂到它的父节点的左子树上。
个人喜欢第2种。
3.4 性能分析
在等概率情况下，完全二叉树的查找效率最高。在随机的情况下，二叉排序树的平均查找长度和O(logn)是等数量级的。
其实看到这了难道不觉得和折半查找的判定树很像嘛，就是平均情况下。两者的原理是一样的。
这里为什么要说“等概率情况”呢，因为有n个结点的二叉排序树并不唯一，平均查找长度与二叉排序树的形态有关，而二叉排序树的形态由关键字的插入顺序决定。比如插入顺序是12345和31254构造的排序树是不同的。前者深度大，查找效率自然低了（前者其实等价于顺序查找）。
怎样可以忽略关键字的插入顺序呢，这就是下面要介绍的平衡二叉排序树了。
4 平衡二叉树（AVL树）
4.1 定义
平衡二叉树（AVL树）：它或者是一棵空树，或者是满足下列性质的二叉树：
- 其左、右子树深度之差的绝对值不大于1
- 其左、右子树都是平衡二叉树
害，怎么说呢，又是一个递归定义。（习惯了）
那么为什么要引入平衡二叉树呢，在二叉排序树的性能分析中我们已经看到，若一棵二叉排序树是平衡的，则树上任何结点的左右子树的深度之差不超过1，二叉树的深度与log2n同数量级。这样就可以保证它的平均查找长度与log2n同数量级。
举个例子：
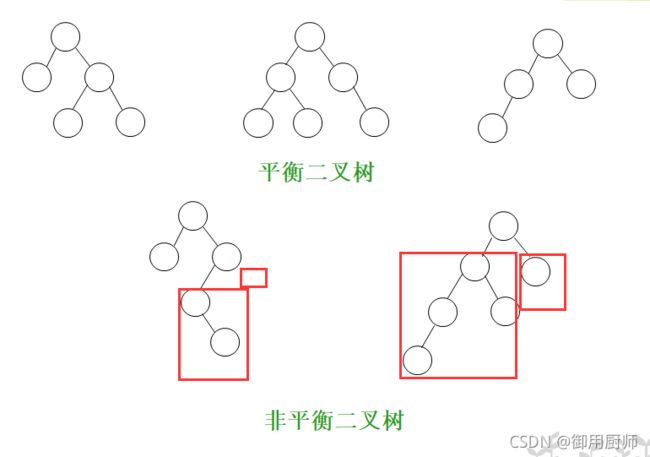
4.2 构造
这里就要介绍一种比较高级的平衡旋转技术：
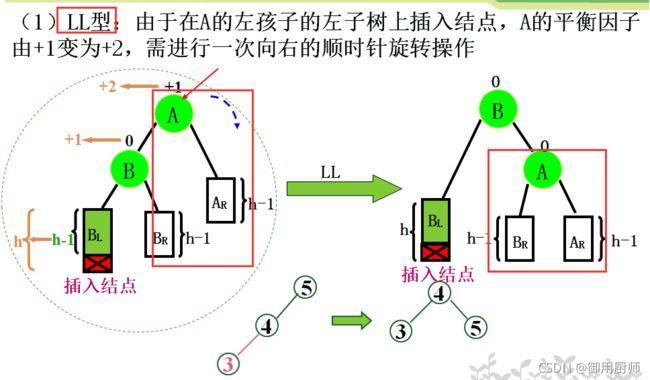
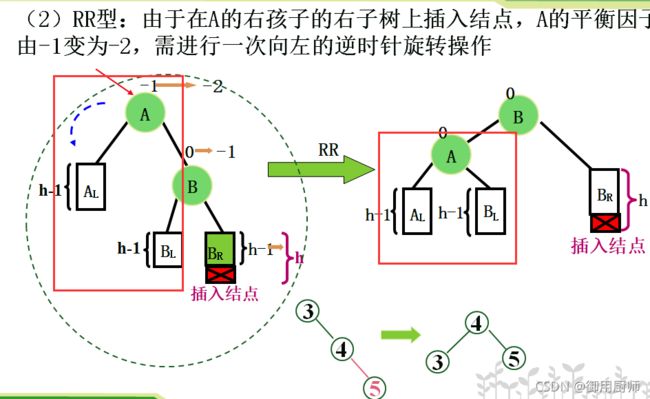
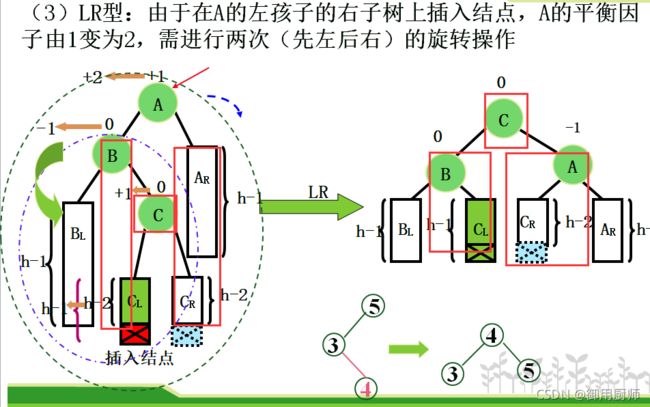
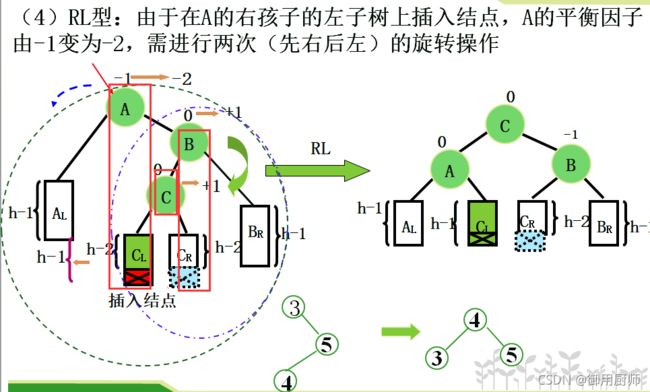
举个例子：10,5,15,12,20,14,30,18,35,2,0,3,4，构造该序列的平衡二叉排序树：
其实没有图片画的那么复杂，这个平衡旋转技术还是很有感觉的。（就描述不出的平衡感
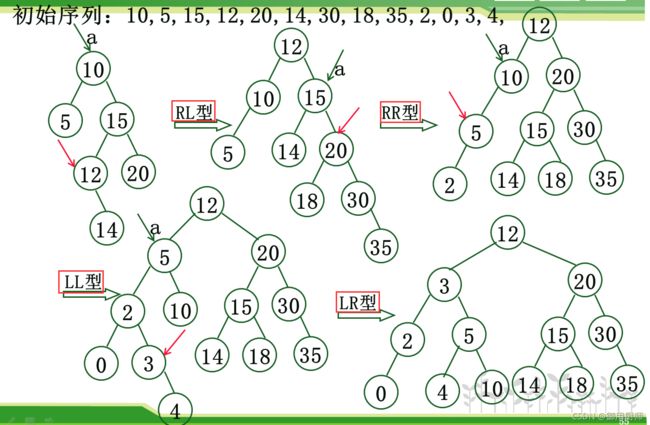
4.3 性能分析
和BST树一样，性能是O(log2n)
5 B-、B+树
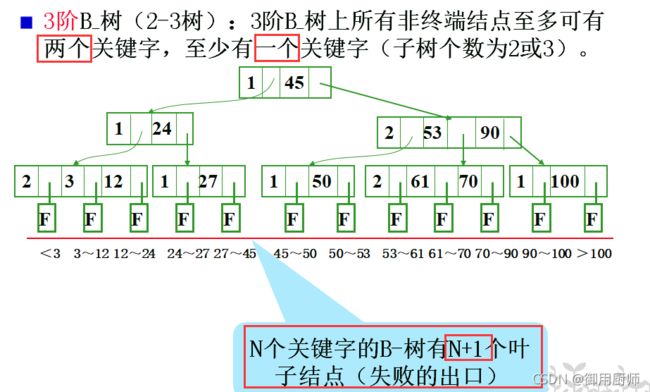
5.1 B-树的定义
这个定义需要强调两点：
- 结点中的关键字个数至多为
m-1（因为每个结点至多有m棵子树） - 根至少有一个关键字（因为若根结点不是叶子结点，至少有两棵子树）
定义还有一个小要求：
给一个B-树的例子，便于理解。
5.2 引入B-树的原因
前面介绍的查找方法适用于待查记录数较小的文件，查找时记录都读入内存中进行处理，统称为内查找法。若文件很大，查找时不能把记录全部读入内存（大量数据仍存放在硬盘上）时，则查找过程需要反复进行内、外存交换。
由于硬盘的驱动受机械运动的制约，速度慢。所以提高查找效率的关键就是减少访问外存的次数。
1970年R bayer和E macreight提出用B-树作为索引组织文件，提高访问速度、减少时间。B-树具有占用存储空间少、查找效率高等优点，常用在文件系统和数据库系统的索引技术中。
举个例子：
用二叉树组织文件，当文件的记录个数为106时，树高平均为17（log2106）。若以256阶B-树组织数据，则树高最多仅为3。
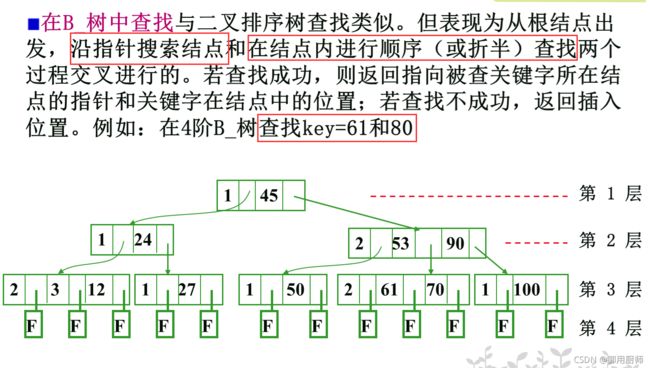
5.3 B-树的查找过程
查找操作的两个过程是：
- 沿指针搜索结点（在磁盘中进行）
- 在结点内进行查找（在内存中进行，因为前一步找到结点后会把结点内的信息读入内存中处理）
在结点内进行查找一般是顺序查找或折半查找，而沿指针搜索结点的过程如下：
从根开始查找，如果 Ki = KEY 则查找成功。
- 若
Ki < KEY < Ki+1; 查找Ai指向的结点 - 若
KEY < K1; 查找A0指向的结点 - 若
KEY > Kn; 查找An指向的结点 - 若 找到叶子，则查找失败。
5.4 B-树的查找分析
在磁盘上进行一次查找比在内存中进行一次查找耗时多很多，因此B-树的查找效率主要取决于访问外设的次数，即：取决于待查关键字所在结点在B-树上的层次数。
比如：
设N＝106，m＝256，则h<=3，即最多访问外存3次可找到所有的记录。
最后提一嘴关于B-树，B树就是B-树，不知道是谁把B-Tree翻译成B-树，误导了当年的我，想当年我一直不知道B树和B-树是一个玩意儿……
5.5 B+树
B+树是B-树的变异树。
一棵m阶B+树和m阶B-树的差异：
- 有
n棵子树的结点中含有n个关键字； - 所有的叶子节点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子节点本身依关键字的大小自小而大顺序链接。
- 所有的非终端节点可以看成是索引部分，结点中仅含有其子树（根结点）中的最大（或最小）关键字
这个定义应该不难理解。
当时B+树没要求掌握，所以课件上给的东西也很少。
5.6 B+树的查找
- 从最小关键字顺序查找
- 从根开始随机查找
6 哈希查找
这个我就不写了，之前写过一篇。可以参考文章：【数据结构】【哈希】哈希表的概念和算法实现
7 总结
最后呢，总结一下查找的时间复杂度：
- 顺序查找：
O(n) - 折半查找：
O(logn)，(O(log2n)) 因为要先快排所以总复杂度为O(nlogn) - 二叉排序树（二叉查找树、BST）：
O(logn)（平均情况下） - 平衡二叉排序树（AVL树）：
O(logn)（O(log2n)） - B树：
O(logn)(O(log2n)) - 哈希查找：
O(1)