时间序列预测
关注微信公众号“时序人”获取更好的阅读体验
时间序列知识整理系列
- 时间序列统计分析
- 时间序列聚类
- 时间序列预测
- 时间序列回归
- 时间序列特征工程
- 时间序列补缺
- 时间序列异常检测
写在前面
时间序列预测就是利用过去一段时间的数据来预测未来一段时间内的信息,包括连续型预测(数值预测,范围估计)与离散型预测(事件预测)等,具有非常高的商业价值。
需要明确一点的是,与回归分析预测模型不同,时间序列模型依赖于数值在时间上的先后顺序,同样大小的值改变顺序后输入模型产生的结果是不同的。如之前的文章所介绍,时间序列可以分为平稳序列,即存在某种周期,季节性及趋势的方差和均值不随时间而变化的序列,和非平稳序列。如何对各种场景的时序数据做准确地预测,是一个非常值得研究的问题。
本文为大家总结时间序列预测的有关方法,浅析这些技术并探索如何可以提高这些方法的预测效果。
基本规则法
要预测一个时间序列,我们首先需要发现其变化的规律。最基本的方法,就是通过人工经验,挖掘时序数据的演化特征,找到时序变化的周期,从而预估时间序列的未来走势。具体的观察一个时间序列,当序列存在周期性时,提取时间序列的周期性特征进行预测。

传统参数法
之前我们介绍了时间序列的统计分析方法,arma。该方法可以将时间序列的演化变为数学参数,天然的,我们可以通过拟合好的模型,进行时间序列的预测。
传统的参数预测方法可以分为两种,一种拟合标准时间序列的餐顺方法,包括移动平均,指数平均等;另一种是考虑多因素组合的参数方法,即AR,MA,ARMA等模型。这类方法比较适用于小规模,单变量的预测,比如某门店的销量预测等。总的来说,基于此类方法的建模步骤是:
- 首先需要对观测值序列进行平稳性检测,如果不平稳,则对其进行差分运算直到差分后的数据平稳;
- 在数据平稳后则对其进行白噪声检验,白噪声是指零均值常方差的随机平稳序列;
- 如果是平稳非白噪声序列就计算ACF(自相关系数)、PACF(偏自相关系数),进行ARMA等模型识别,
- 对已识别好的模型,确定模型参数,最后应用预测并进行误差分析。
这类方法一般是统计或者金融出身的人用的比较多,对统计学或者随机过程知识的要求比较高。而在数据挖掘的场景中比较难适用,因为需要大量的参数化建模。比如有一个连锁门店的销售数据,要预测每个门店的未来销量,用这类方法的话就需要对每个门店都建立模型, 这样就很难操作了。
这类方法可以参考:时间序列统计分析
时间序列分解
时间序列分解法是数年来一直非常有用的方法,一个时间序列往往是一下几类变化形式的叠加或耦合:
- 长期趋势(Secular trend, T):长期趋势指现象在较长时期内持续发展变化的一种趋向或状态。
- 季节变动(Seasonal Variation, S):季节波动是由于季节的变化引起的现象发展水平的规则变动
- 循环波动(Cyclical Variation, C):循环波动指以若干年为期限,不具严格规则的周期性连续变动
- 不规则波动(Irregular Variation, I): 不规则波动指由于众多偶然因素对时间序列造成的影响
时间序列分解模型
加法模型
加法模型的形式如下:
X t = T t + S t + C t + I t X_t = T_t + S_t + C_t + I_t Xt=Tt+St+Ct+It
加法模型中的四种成分之间是相互独立的,某种成分的变动并不影响其他成分的变动。各个成分都用绝对量表示,并且具有相同的量纲。
乘法模型
乘法模型的形式如下:
X t = T t × S t × C t × I t X_t = T_t \times S_t \times C_t \times I_t Xt=Tt×St×Ct×It
乘法模型中四种成分之间保持着相互依存的关系,一般而言,长期趋势用绝对量表示,具有和时间序列本身相同的量纲,其他成分则用相对量表示。
加乘混合模型
以上两种方式的混合
时间序列的长期趋势分析
移动平均法
在原时间序列内依次求连续若干期的平均数作为其某一期的趋势值,如此逐项递移求得一系列的移动平均数,形成一个平均数时间序列。
时间回归法
使用回归分析中的最小二乘法,以时间t或t的函数为自变量拟合趋势方程。常用的趋势方程如下:
- 一阶线性方程
- 二次(多次)方程曲线
- 指数曲线
时间序列季节变动分析
时间序列短期会受季节等短期因素影响,从而存在一些周期性
乘法模型-季节指数
乘法模型中的季节成分通过季节指数来反映。常用的方法称为移动平均趋势剔除法。步骤如下:
- 计算一动平均值
- 从序列中剔除移动平均值
- 季 节 指 数 ( S ) = 同 季 平 均 数 总 季 平 均 数 × 100 % 季节指数(S) = \frac{同季平均数}{总季平均数}\times 100\% 季节指数(S)=总季平均数同季平均数×100%
时间序列循环变动分析
时序长期来看会存在一个循环往复,通常通过剩余法来计算循环变动成分C:
- 如果有季节成分,计算季节指数,得到季节调整后的数据TCI
- 根据趋势方程从季节调整后的数据中消除长期趋势,得到序列CI
- 对消去季节成分和趋势值的序列CI进行移动平均以消除不规则波动 ,得到循环变动成分C
时间序列不规则变动分析

除了以上三种变动信息,剩下的为不规律的时序变动信息。如有需要,可以进一步分解出不规则变动成分:
I = T × S × C × I T × S × C I = \frac{T \times S \times C \times I}{T \times S \times C} I=T×S×CT×S×C×I
对于一个时间序列,剔除长期趋势,季节性,循环变动因素之后,剩下的就是不规则变动因素
Prophet
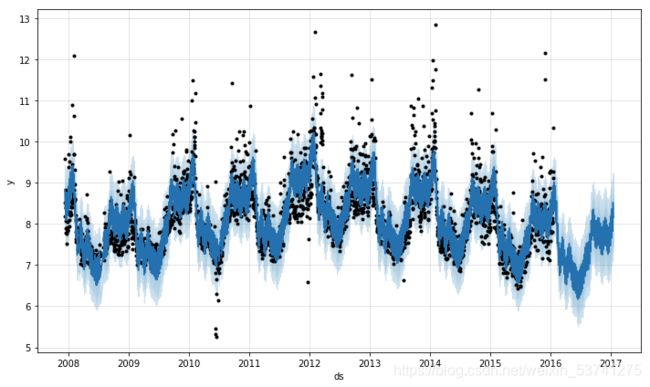
这里特别提一个Facebook 所服务化的时间序列预测工具,prophet,官网可以参考官网说明(英文)。该方法类似于STL时序分解的思路,增加考虑节假日等信息对时序变化的影响。
机器学习
近年来时间序列预测方法,多采用机器学习方式。机器学习的方法,主要是构建样本数据集,采用“时间特征”到“样本值”的方式,通过有监督学习,学习特征与标签之前的关联关系,从而实现时间序列预测。常用的场景有:
单步预测
在时间序列预测中的标准做法是使用滞后的观测值 x t − 1 x_{t-1} xt−1,作为输入变量来预测当前的时间的观测值 x t x_t xt。这被称为单步单变量预测。
多步预测
另一种预测问题类型是使用过去的观测序列 { x t − 1 , x t − 2 , . . . } \{x_{t-1},x_{t-2},...\} {xt−1,xt−2,...}来预测未来的观测序列 { x t , x t + 1 , . . . } \{x_t, x_{t+1},...\} {xt,xt+1,...}。这就是多步预测或序列预测。
多变量预测
另一个重要的时间序列称为多元时间序列,即每个时间有多个观测值, { X t = ( x t a , x t b , x t c , . . . ) } t T \{X_t=(x_t^a, x_t^b, x_t^c,...)\}_t^T {Xt=(xta,xtb,xtc,...)}tT。这意味着我们通过不同的测量手段得到了多种观测值,并且希望预测其中的一个或几个值。例如,我们可能有两组时间序列观测值 { x t − 1 a , x t − 2 a , . . . } \{x_{t-1}^a, x_{t-2}^a,...\} {xt−1a,xt−2a,...}, { x t − 1 b , x t − 2 b , . . . } \{x_{t-1}^b, x_{t-2}^b,...\} {xt−1b,xt−2b,...},我们希望分析这组多元时间序列来预测 x t a x_t^a xta。
基于以上场景,许多监督学习的方法可以应用在时间序列的预测中,比如svm/xgboost/逻辑回归/回归树/…
深度学习
深度学习方法近年来逐渐替代机器学习方法,成为人工智能与数据分析的主流,对于时间序列的分析,有许多方法可以进行处理,包括:循环神经网络-LSTM模型/卷积神经网络/基于注意力机制的模型(seq2seq)
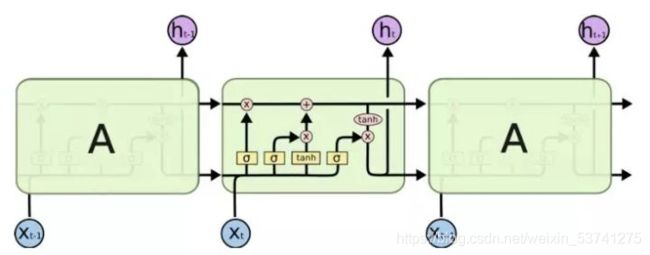
循环神经网络
循环神经网络(RNN)框架及其变种(LSTM/GRU/…)是为处理序列型而生的模型,天生的循环自回归的结构是对时间序列的很好的表示。所采用的方式也是监督学习,不过不需要人为的构建时序特征,可以通过深度学习网络拟合时序曲线,捕捉时间先后顺序关系,长期依赖,进行特征学习与预测。
卷积神经网络
传统的卷积神经网络(CNN)一般认为不太适合时序问题的建模,这主要由于其卷积核大小的限制,不能很好的抓取长时的依赖信息。 但是最近也有很多的工作显示,特定的卷积神经网络结构也可以达到很好的效果,
Gramian Angular Field (格拉姆角场GAF)
方法描述:将笛卡尔坐标系下的一维时间序列,转化为极坐标系表示,再使用三角函数生成GAF矩阵。
计算过程:
- 数值缩放:将笛卡尔坐标系下的时间序列缩放到[0,1]或[-1,1]区间
- 极坐标转换:使用坐标变换公式,将笛卡尔坐标系序列转化为极坐标系时间序列
- 角度和/差的三角函数变换:若使用两角和的cos函数则得到GASF,若使用两角差的cos函数则得到GADF
Short Time Fourier Transform (短时傅里叶变换STFT)
方法描述:在语音信号处理场景使用很广泛,其目标主要将时间序列转为时频图像,进而采用卷积网络进行特征分析。

时间卷积网络
时间卷积网络(TCN)是一种特殊的卷积神经网络,针对一维空间做卷积,迭代多层捕捉长期关系。具体的,对于上一层t时刻的值,只依赖于下一层t时刻及其之前的值。和传统的卷积神经网络的不同之处在于,TCN不能看到未来的数据,它是单向的结构,不是双向的。也就是说只有有了前面的因才有后面的果,是一种严格的时间约束模型,因此又被称为因果卷积。
基于注意力机制的模型
在RNN中分析时间序列需要我们一步步的顺序处理从 t-n 到 t 的所有信息,而当它们相距较远(n非常大)时RNN的效果常常较差,且由于其顺序性处理效率也较低。基于注意力机制(Attention)的模型,采用跳步的方式计算每个数值之间的两两关联,然后组合这些关联分数得到一个加权的表示。该表示通过前馈神经网络的学习,可以更好的考虑到时序的上下文的信息。
结合CNN+RNN+Attention,作用各不相同互相配合
主要设计思想:
- CNN捕捉短期局部依赖关系
- RNN捕捉长期宏观依赖关系
- Attention为重要时间段或变量加权
一些需要注意的
难点:
- 理解时间序列预测问题是要用历史数据预测未来数据
- 时间序列问题的训练集、测试集划分
- 特征工程方法及过程
- 如何转化为监督学习数据集
- LSTM计算过程理解,包括输入输出维度、参数数量等
- seq2seq过程的理解,decoder实现
- attention注意力机制的原理及实现,包括encoder-decoder attention, self attention, multi-head attention等
- 时间卷积网络的含义,dilated-convolution 和 causal-convolution
- prophet预测原理,各参数对模型拟合效果、泛化效果的影响
- 时间序列基本规则法中周期因子得计算过程
- 传统方法如周期因子、线性回归、ARMA等的预测结果表现为,预测趋势大致正确,但对波动预测不理想,体现在波动的幅度差异、相位偏移。
- 时间序列分解方法。理解加法模型和乘法模型,判断分解模型的选取及分解技巧。
工具
- tslearn:开源的时间序列机器学习python工具包
- tsfresh:开源的时间序列特征提取python工具包
- pyts:开源的时间序列分类Python工具包。提供预处理工具及若干种时间序列分类算法
更多原创内容与系列分享,欢迎关注微信公众号“时序人”获取。
![]()