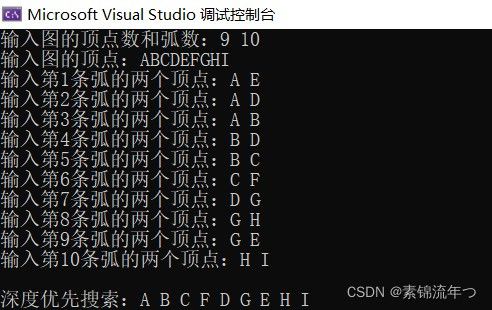
【数据结构】图的遍历（深度优先搜索、广度优先搜索）及简单路径问题（C语言）
目录
-
- 1. 深度优先搜索
-
- 1.1 深度优先搜索步骤
- 1.2 邻接矩阵方式实现深度优先搜索连通图
- 1.3 邻接表方式实现深度优先搜索连通图
- 2. 广度优先搜索
-
- 2.1 广度优先搜索步骤
- 2.2 邻接矩阵方式实现广度优先搜索连通图
- 2.2 邻接表方式实现广度优先搜索连通图
- 3. 图的简单路径
图的遍历就是从图中的某个顶点出发，按某种方法对图中所有顶点访问且仅访问一次。图的遍历算法是求解图的连通性问题、拓扑排序和关键路径等算法的基础。
为了保证图中各个顶点在遍历过程中访问且仅访问一次，需要为每个顶点设一个访问标志，因此要为图设置一个访问标志数组visited[n]，用于标示图中每个顶点是否被访问过。
对于图的遍历，通常有两种方法，即深度优先搜索和广度优先搜索。这两种遍历方法对于无向图和有向图均适用。图的深度优先搜索和广度优先搜索结果均不唯一。
1. 深度优先搜索
深度优先搜索（Depth-First Search，DFS）是指按照深度方向搜索，它类似于树的先根遍历，是树的先根遍历的推广。
1.1 深度优先搜索步骤
深度优先搜索基本步骤：
① 从图中某个顶点v0出发，首先访问v0。
② 找出刚访问过顶点的第一个未被访问的邻接点，然后访问该顶点。以该顶点为新顶点，重复此步骤，直到刚访问过的顶点没有未被访问的邻接点为止。
③ 返回前一个访问过的且仍有未被访问过的邻接点的顶点，找出该顶点的下一个未被访问的邻接点，访问该顶点；然后执行步骤②。
示例：
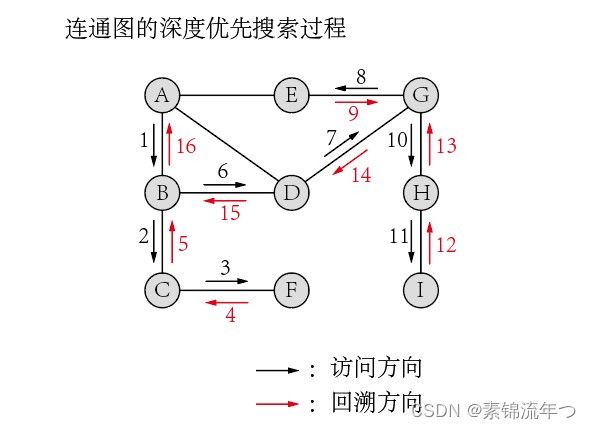
首先访问A，从A出发；
（1）A未访问的邻接点有B、D、E，首先访问B；
（2）B未访问的邻接点有C、D，首先访问C；
（3）C未访问的邻接点为F，访问F；
（4）F没有未访问的邻接点，回溯到C；
（5）C没有未访问的邻接点，回溯到B；
（6）B未访问的邻接点为D，访问D；
（7）D未访问的邻接点为G，访问G；
（8）G未访问的邻接点有E、H，首先访问E；
（9）E没有未访问的邻接点，回溯到G；
（10）G未访问的邻接点为H，访问H；
（11）H未访问的邻接点为I，访问I；
（12）I没有未访问的邻接点，回溯到H；
（13）H没有未访问的邻接点，回溯到G；
（14）G没有未访问的邻接点，回溯到D；
（15）D没有未访问的邻接点，回溯到B；
（16）B没有未访问的邻接点，回溯到A；
至此，深度优先搜索结束，相应的访问序列为：A，B，C，F，D，G，E，H，I；
上图中所有顶点加上标有黑色箭头的边，构成一棵以A为根的树，称为深度优先搜索树。
注意：当一个顶点有多个未被访问的邻接点时，选择作为下一次访问的点的顺序可能不一样，因此图的深度优先搜索结果不唯一！
1.2 邻接矩阵方式实现深度优先搜索连通图
用邻接矩阵方式实现深度优先搜索连通图
/*用邻接矩阵方式实现深度优先搜索*/
int visited[MAX_VERTEX_NUM] = { 0 }; //访问标志数组
void DepthFirstSearch(AdjMatrix G, int v0) {
printf("%c ", G.vertex[v0]);
visited[v0] = 1; //置1表示已访问过
for (int i = 0; i < G.vexnum; i++) {
if (!visited[i] && G.arcs[v0][i].adj == 1)
DepthFirstSearch(G, i);
}
}
完整实现代码
# include运行结果
1.3 邻接表方式实现深度优先搜索连通图
用邻接表方式实现深度优先搜索连通图
/*用邻接表方式实现深度优先搜索*/
int visited[MAX_VERTEX_NUM] = { 0 }; //访问标志数组
void DepthFirstSearch(AdjList G, int v0) {
printf("%c ", G.vertex[v0]);
visited[v0] = 1; //置1表示已访问过
ArcNode* p;
p = G.vertex[v0].firstarc;
while (p != NULL) {
if (!visited[p->adjvex])
DepthFirstSearch(G, p->adjvex);
p = p->nextarc;
}
}
完整实现代码
/*图的邻接表表示法*/
typedef char VertexData;
//弧结点结构
typedef struct ArcNode {
int adjvex; //该弧指向顶点的位置
struct ArcNode* nextarc; //指向下一条弧的指针
int info; //与弧相关的信息
}ArcNode;
//表头结点结构
typedef struct VertexNode {
VertexData data; //顶点数据
ArcNode* firstarc; //指向该顶点的第一条弧的指针
}VertexNode;
//邻接表结构
typedef struct {
VertexNode vertex[MAX_VERTEX_NUM];
int vexnum, arcnum; //图的顶点数和弧数
}AdjList;
AdjList G;
/*求顶点位置*/
int LocateVertex(AdjList* G, VertexData v) {
int k;
for (k = 0; k < G->vexnum; k++) {
if (G->vertex[k].data == v)
break;
}
return k;
}
/*创建图的邻接表*/
int CreateAdjList(AdjList* G) {
int i, j, k;
VertexData v1, v2;
ArcNode* p;
printf("输入图的顶点数和弧数："); //输入图的顶点数和弧数
scanf("%d%d", &G->vexnum, &G->arcnum);
printf("输入图的顶点：");
for (i = 0; i < G->vexnum; i++) { //输入图的顶点，初始化顶点结点
scanf(" %c", &(G->vertex[i].data));
G->vertex[i].firstarc = NULL;
}
for (k = 0; k < G->arcnum; k++) {
printf("输入第%d条弧的两个顶点：", k + 1);
scanf(" %c %c", &v1, &v2); //输入一条弧的两个顶点
i = LocateVertex(G, v1);
j = LocateVertex(G, v2);
p = (ArcNode*)malloc(sizeof(ArcNode)); //申请新弧结点
p->adjvex = j;
p->nextarc = G->vertex[i].firstarc;
G->vertex[i].firstarc = p;
}
}
/*用邻接表方式实现深度优先搜索*/
int visited[MAX_VERTEX_NUM] = { 0 }; //访问标志数组
void DepthFirstSearch(AdjList G, int v0) {
printf("%c ", G.vertex[v0]);
visited[v0] = 1; //置1表示已访问过
ArcNode* p;
p = G.vertex[v0].firstarc;
while (p != NULL) {
if (!visited[p->adjvex])
DepthFirstSearch(G, p->adjvex);
p = p->nextarc;
}
}
int main() {
AdjList G;
CreateAdjList(&G);
printf("\n深度优先搜索：");
DepthFirstSearch(G, 0);
return 0;
}
运行结果
2. 广度优先搜索
广度优先搜索（Breadth-First Search）是指按照广度方向搜索，它类似于树的层次遍历，是树的按层次遍历的推广。
2.1 广度优先搜索步骤
广度优先搜索基本步骤：
① 从图中某个顶点v0出发，首先访问v0。
② 依次访问v0的各个未被访问的邻接点。
③ 分别访问这些邻接点的各个未被访问的邻接点。重复③直至所有顶点均被访问。
示例：
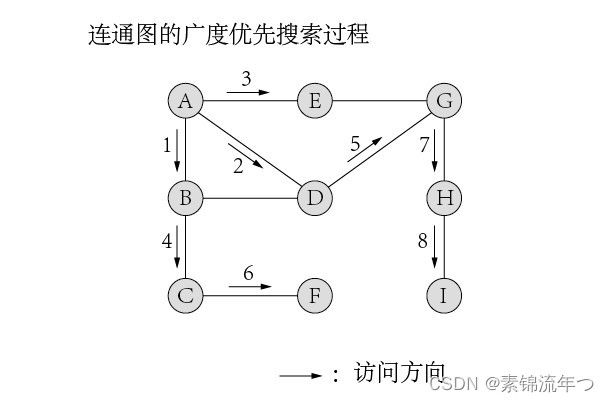首先访问A，从A出发；
（1）A的未访问邻接点有B、D、E，首先访问B；
（2）访问A的第二个未访问邻接点D；
（3）访问A的第三个未访问邻接点E；
（4）因B在D、E前被访问，故访问B的未访问邻接点C；
（5）因D在E、C前被访问，故访问D的未访问邻接点G；
（6）因E在C、G前被访问，且E没有未访问邻接点，故访问C的未访问邻接点F；
（7）因G在F前被访问，故访问G的未访问邻接点H；
（8）因F在H前被访问，且F没有未访问邻接点，故访问H的未访问邻接点I；
至此，广度优先搜索结束，相应的访问序列为：A，B，D，E，C，G，F，H，I；
上图中所有顶点加上标有箭头的边，构成一棵以A为根的树，称为广度优先搜索树。
注意：当一个顶点有多个未被访问的邻接点时，选择作为下一次访问的点的顺序可能不一样，因此图的广度优先搜索结果不唯一！
2.2 邻接矩阵方式实现广度优先搜索连通图
用邻接矩阵方式实现广度优先搜索连通图
/*邻接矩阵实现广度优先搜索*/
int visited[MAX_VERTEX_NUM] = { 0 }; //访问标志数组
void BreadthFirstSearch(AdjMatrix G, int v0) {
int queue[MAX_VERTEX_NUM]; //一维数组模拟队列操作
int rear = 0, front = 0, v; //模拟队尾指针和队头指针
printf("%c ", G.vertex[v0]);
visited[v0] = 1;
queue[rear] = v0; //模拟入队
while (rear >= front) {
v = queue[front]; //模拟取队头元素
front++; //模拟出队
for (int i = 0; i < G.vexnum; i++) {
if (G.arcs[v][i].adj == 1 && !visited[i]) {
printf("%c ", G.vertex[i]);
visited[i] = 1;
rear++;
queue[rear] = i; //模拟入队
}
}
}
}
完整实现代码
# include运行结果
2.2 邻接表方式实现广度优先搜索连通图
用邻接表方式实现广度优先搜索连通图
/*邻接表实现广度优先搜索*/
int visited[MAX_VERTEX_NUM] = { 0 }; //访问标志数组
void BreadthFirstSearch(AdjList G, int v0) {
int queue[MAX_VERTEX_NUM]; //一维数组模拟队列操作
int rear = 0, front = 0, v; //模拟队尾指针和队头指针
ArcNode* p;
printf("%c ", G.vertex[v0]);
visited[v0] = 1;
queue[rear] = v0; //模拟入队
while (rear >= front) {
v = queue[front]; //模拟取队头元素
front++; //模拟出队
p = G.vertex[v].firstarc;
while (p != NULL) {
if (!visited[p->adjvex]) {
printf("%c ", G.vertex[p->adjvex]);
visited[p->adjvex] = 1;
rear++;
queue[rear] = p->adjvex; //模拟入队
}
p = p->nextarc;
}
}
}
完整实现代码
# include运行结果
3. 图的简单路径
找出图中从顶点u到顶点v的一条简单路径。
若表示路径的顶点序列中的顶点各不相同，则称该路径为简单路径，图中两顶点间的简单路径不唯一。
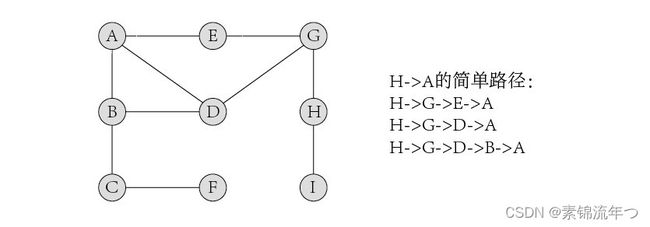
思路：基于深度优先搜索来搜索路线。设置pre数组记录搜索路线，当从顶点vi遍历其邻接点vj时，将pre[j]置为i，以便于搜索结束后输出路径。可用pre数组代替visited数组，pre[j]=-1表示vj未被访问。
完整代码
# include运行结果
参考：耿国华《数据结构——用C语言描述（第二版）》
更多数据结构内容关注我的《数据结构》专栏：https://blog.csdn.net/weixin_51450101/category_11514538.html?spm=1001.2014.3001.5482