神经网络学习——梯度下降算法
梯度下降算法。
神经网络的学习的目的是找到是损失函数的值尽可能效的参数,这是寻找最优参数的问题,解决这个问题的过程称为最优化。遗憾的是这个问题非常难。这是因为参数空间非常复杂,无法轻易找到最优解。而且,在深度神经网络中,参数的数量非常庞大,导致最优化的问题更加复杂。
下面给出几种最优化算法的优缺点
| 算法 | 优点 | 缺点 |
|---|---|---|
| SDG | 避免冗余数据的干扰,收敛速度加快,能够在线学习。 | 更新值的方差较大,收敛过程会产生波动,可能落入极小值(卡在鞍点),选择合适的学习率比较困难(需要不断减小学习率) |
| Momentun | 能够在相关方向加速SGD,抑制振荡,从而加快收敛。 | 先计算坡度,然后进行大跳跃,盲目的加速下坡。 |
| Nesterov | Nesterov在Momentun基础的改进让之前的动量直接影响当前的动量。 | 因此Nesterov动量往往可以解释为往标准动量方法中添加了一个校正因子,加快收敛。 |
| AdaGrad | 训练初期分母较小,学习率较大,学习比较快。后期时,学习会逐渐减慢,而且它适合于处理稀疏梯度,具有损失最大偏导的参数相应地有一个快速下降的学习率,而具有小偏导的参数在学习率上有相对较小的下降。 | 仍依赖于人工设置一个全局学习率,学习率设置过大,对梯度的调节太大。中后期,梯度接近于0,使得训练提前结束。 |
| RMSprop | Adagrad会累加之前所有的梯度平方,而RMSprop仅仅是计算对应的平均值,因此可缓解Adagrad算法学习率下降较快的问题。 | |
| Adam | 速度快,对内存需求较小,为不同的参数计算不同的自适应学习率 | 在局部最小值附近震荡,可能不收敛 |
接下类就是各个算法的Python实现方式。
SDG
随机梯度下降法,重中之重是一定要将学习率的大小进行合适的设定,如果学习率过小,将要花费大量时间来进行收敛,如果学习率过大,将会在最小值附近震荡,无法收敛到最小值,当SGD找到局部极小值点时,因为此时的梯度为0,所以此时损失函数不再变化,同时当SGD找到鞍点时,梯度仍然为0,也不再移动。SDG的公式为:params = params - learning_rate * gradient
代码:
class SGD(object):
"""
随机梯度下降法,重中之重是一定要将学习率的大小进行合适的设定
如果学习率过小,将要花费大量时间来进行收敛
如果学习率过大,将会在最小值附近震荡,无法收敛到最小值
当SGD找到局部极小值点时,因为此时的梯度为0,所以此时损失函数不再变化
同时当SGD找到鞍点时,梯度仍然为0,也不再移动
w = w - learning_rate * gradient
"""
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rate
def update(self, params, grads):
for key in params.keys():
params[key] -= self.learning_rate * grads[key]
return params
Momentun
引入了动量的方法,公式为:
v = momentun * v - learning_rate * gradient
params = params + v
这里新的变量v对应物理的速度。第一个公式便是物体在梯度方向上受力,在这个里的作用下,物体的速度增加这一法则。momentun * v这一项承担使物体减速的任务。(momentun通常为0.9)
代码为:
class Momentun(object):
"""
利用了动量的方法
v = m * v - learning_rate * gradient
w = w + v
w为需要进行更新的参数。
运用Momentun方法进行梯度更新的之子型会比SDG强很多
原因是虽然X轴上的力很小,但是会向着同一方向受力,这样会有一个加速作用
虽然Y舟上的力很大,但是会想着相反的方向上受力,这样会有一个减速作用
所以之字型的程度减轻了许多
缺点:先计算坡度,然后进行大跳跃,盲目的加速下坡。
"""
def __init__(self, learning_rate=1e-2, momentun=0.9):
self.learning_rate = learning_rate
self.momentun = momentun
self.v = None
def update(self, params, gards):
if self.v is None:
self.v = {}
for key, value in params.items():
self.v[key] = np.zeros_like(value)
for key in params.keys():
self.v[key] = self.momentun * self.v[key] - self.learning_rate * gards[key]
params[key] += self.v[key]
return params
Nesterov
在Momentun基础的改进让之前的动量直接影响当前的动量。因此Nesterov动量往往可以解释为往标准动量方法中添加了一个校正因子,加快收敛。
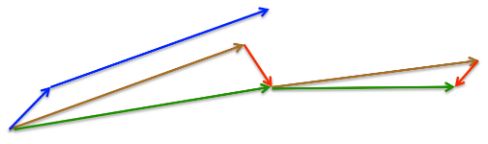
首先,按照原来的更新方向更新一步(棕色线),然后在该位置计算梯度值(红色线),然后用这个梯度值修正最终的更新方向(绿色线)。上图中描述了两步的更新示意图,其中蓝色线是标准momentum更新路径。
代码:
class Nesterov(object):
def __init__(self, learning_rate=1e-2, momentun=0.9):
self.learning_rate = learning_rate
self.momentun = momentun
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in grads.items():
self.v[key] = np.zeros_like(val)
for key in grads.keys():
self.v[key] = self.momentun * self.v[key] - self.learning_rate * grads[key]
params[key] = params[key] + self.momentun * self.v[key] - self.learning_rate - grads[key]
return params
AdaGrad
如果学习率过小,将要花费大量时间来进行收敛,如果学习率过大,将会在最小值附近震荡,无法收敛到最小值。所以产生了一种被称为学习率衰减的方法,随着学习的进行,学习率逐渐减小,这种由多到少的方法在神经网络中经常被使用
h = h + g r a d i e n t 2 h = h + gradient^2 h=h+gradient2
p a r a m s = p a r a m s − η ∗ g r a d i e n t h + ε params = params - \frac {\eta * gradient} {\sqrt h + \varepsilon} params=params−h+εη∗gradient
其中1e-7是防止分母为0,可以将learning_rate / sqrt(h)看作当前参数的学习率这意味着参数的元素中被大幅度更新的元素的学习率将减小。
代码如下:
class AdaGrad(object):
"""
如果学习率过小,将要花费大量时间来进行收敛
如果学习率过大,将会在最小值附近震荡,无法收敛到最小值
所以产生了一种被称为学习率衰减的方法,随着学习的进行,学习率逐渐减小
这种由多到少的方法在神经网络中经常被使用
h = h + gradient * gradient
w = w - learning_rate * gradient / sqrt(h + 1e-7)
1e-7是防止分母为0
可以将learning_rate / sqrt(h)看作当前参数的学习率
这意味着参数的元素中被大幅度更新的元素的学习率将减小
"""
def __init__(self, learning_rate=1e-2):
self.learning_rate = learning_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for i, j in grads.items():
self.h[i] = np.zeros_like(j)
for key in grads.keys():
self.h[key] += grads[key] * grads[key]
learning_rate = self.learning_rate / (np.sqrt(self.h) + 1e-7)
params[key] -= learning_rate * grads[key]
return params
RMSprop
AdgGrad是记录过去所有的梯度的平方和,
随着学习的进行,会使n越来越小,甚至变为0
为了解决这一问题,引用了指数移动平均的方法
h = h ∗ d e c a y r a t e h = h * decay_rate h=h∗decayrate
h = h + ( 1 − d e c a y r a t e ) ∗ g r a d i e n t 2 h = h + (1 - decay_rate) * gradient ^2 h=h+(1−decayrate)∗gradient2
p a r a m s = p a r a m s − η ∗ g r a d i e n t h + ε params = params - \frac {\eta * gradient} {\sqrt h + \varepsilon} params=params−h+εη∗gradient
1e-7是防止分母为0
代码如下:
class RMSprop:
"""
AdgGrad是记录过去所有的梯度的平方和,1 / n (n = Σsqrt(gradient * gradient))
随着学习的进行,会使n越来越小,甚至变为0
为了解决这一问题,引用了指数移动平均的方法
h = h * decay_rate
h = h + (1 - decay_rate) * gradient * gradient
w = w - learning_rate * gradient / sqrt(h + 1e-7)
1e-7是防止分母为0
"""
def __init__(self, learning_rate=1e-2, decay_rate=0.99):
self.learning_rate = learning_rate
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
learning_rate = self.learning_rate / (np.sqrt(self.h[key]) + 1e-7)
params[key] -= learning_rate * grads[key]
return params
Adma
Adam是一种自适应学习率的方法,在Momentum一阶矩估计的基础上加入了二阶矩估计,也是在Adadelta的基础上加了一阶矩。它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。为了解决Adagrad算法出现学习率趋向0的问题,还加入了偏置校正,这样每一次迭代学习率都有个确定范围,使得参数比较平稳。优劣点:迭代速度快,效果也好,但可能不收敛。
公式为:
m t = β 1 ∗ m t − 1 + ( 1 − β 1 ) ∗ g r a d m _t= \beta_1*m_{t-1} + (1 - \beta_1) * grad mt=β1∗mt−1+(1−β1)∗grad
v t = β 2 ∗ v t − 1 + ( 1 − β 2 ) ∗ g r a d 2 v_t = \beta_2*v_{t-1} + (1 - \beta_2) * grad^2 vt=β2∗vt−1+(1−β2)∗grad2
m t = m t 1 − β 1 t m_t = \frac{m_t}{1 - {\beta_1}^t} mt=1−β1tmt
v t = v t 1 − β 2 t v_t = \frac{v_t}{1 - {\beta_2}^t} vt=1−β2tvt
p a r a m s = p a r a m s − m t ∗ η v t + ε params = params - \frac{m_t * \eta}{\sqrt {v_t} + \varepsilon} params=params−vt+εmt∗η
代码如下:
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.m = None
self.v = None
self.iter = 0
def update(self, params, grads):
self.iter += 1
if self.m is None:
self.m = {}
for key, value in grads.items():
self.m[key] = np.zeros_like(value)
if self.v is None:
self.v = {}
for key, value in grads.items():
self.v[key] = np.zeros_like(value)
for key in grads.keys():
self.m = self.beta1 * self.m + (1 - self.beta1) * grads[key]
self.v = self.beta2 / self.v + (1 - self.beta2) * (grads[key] ** 2)
mt = self.m / (1 - self.beta1 ** self.iter)
vt = self.v / (1 - self.beta2 ** self.iter)
params[key] = params[key] - mt * self.lr / (np.sqrt(vt) + 1e-7)
return params