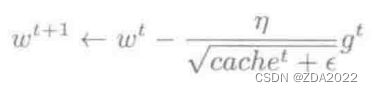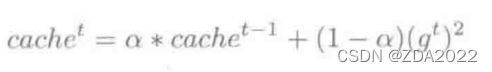读书笔记-深度学习入门之pytorch-第三章（含全连接方法实现手写数字识别）（详解）

目录

1、张量

2、分类问题

3、激活函数

（1）sigmoid函数

（2）Tanh函数 

（3）ReLU函数

（4）SoftMax函数

（5）Maxout函数 

4、模型表示能力

5、反向传播算法

6、优化算法

（1）torch.optim.SGD 

（2） torch.optim.Adagrad：​

（3）torch.optim.RMSprop

（4）torch.optim.Adadelta

（5）torch.optim.Adam(AMSGrad)（实际中常用）

（6）torch.optim.Adamax

（7）torch.optim.SparseAdam

（8） torch.optim.AdamW

（9） torch.optim.ASGD

（10）torch.optim.LBFGS

（11）torch.optim.Rprop

7、处理数据和训练模型的技巧

（1）预处理阶段：

（2）权重初始化

（3）防止过拟合：

8、多层全连接层实现手写数字识别

---

1、张量

参考:pytorch张量(tensor)运算小结_小小鸟要高飞的博客-CSDN博客_pytorch tensor运算

import torch

a = torch.Tensor([[2, 3],
                  [4, 8],
                  [7, 9]])
b = torch.Tensor([[1, 2],
                  [2, 3],
                  [3, 4]])
c = torch.Tensor([[3, 4],
                  [2, 3]])
print(a.size())  # a为3*2的张量
print(torch.mm(a, c))  # 两张量相乘
print(torch.cat((a, b), 1))  # 两张量拼接
print(torch.mul(a, b))  # 两维度相同的张量对应元素相乘
print(torch.inverse(c))  # 张量求逆

d = c.numpy()  # 张量转变为数组
print(d)
print(type(d))
e = torch.from_numpy(d)  # 数组转变为张量
print(e)
print(type(e))

2、分类问题

监督学习分为回归问题与分类问题

Logistic回归：二分类问题中，是希望能找到一个区分度足够好的决策边界将两类分开

3、激活函数

存在必要性：如果没有激活函数的话，神经元的信号处理本质上就是一个线性组合，即使叠加再多层的神经元，整个神经网络也还是线性组合，这样就不能解决非线性的问题，所以激活函数的作用，是为神经网络引入非线性组合的能力，使其可以适用于复杂的应用场景。

正样本让激活函数激活变大，负样本让激活函数激活变小

（1）sigmoid函数

缺点：1>造成梯度消失，对多层网络十分不友好

           2>sigmoid函数输出是非零均值的

           3>收敛速度慢

（2）Tanh函数 

 解决了sigmoid函数中零均值问题，但依旧存在梯度消失问题

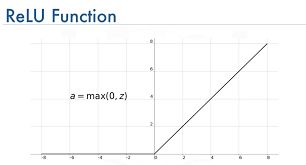
（3）ReLU函数

优点：1>简单

           2>解决了梯度消失问题

缺点：1>对于负数，其导数为0，此时会出现神经元的参数永远无法更新的情况称之为神经元死亡，造成这种现象的原因由两个，第一种是在初始化参数时出现负值，第二种是学习率设置较大，导致参数更新幅度太大，出现负值。所以在使用ReLU时，对学习率的设置要注意，需要一个合适的较小的学习率

（4）SoftMax函数

作为输出层的激活函数，专门用于处理多分类问题

（5）Maxout函数 

maxout是由人为设定的K个神经元构成的一层神经元，示意如下

对于maxout层的输出，取k个神经元输出值的最大值作为最终的输出值，这就是maxout的含义。maxout可以看作是分段的线性函数，可以拟合任意的凸函数，提供模型的拟合能力。

引入maxout层，意味着额外增加了一层权重和参数，使得神经网络整体的参数变多，计算量更大。

4、模型表示能力

1>拥有至少一个隐藏层的神经网络可以逼近任何连续函数 

2>过拟合：模型复杂，但忽略了潜在的数据关系，将噪声放大了

5、反向传播算法

能够自动求导，从而根据导数来更新网络参数

6、优化算法

梯度下降：

（1）torch.optim.SGD 

torch.optim.SGD 可实现SGD优化算法，带动量SGD优化算法，带 NAG(Nesterov accelerated gradient) 动量SGD优化算法，并且有 weight_decay 项。

torch.optim.SGD(params, 
                lr=, 
                momentum=0, 
                dampening=0, 
                weight_decay=0, 
                nesterov=False)

params (iterable)：参数组，优化器要管理的那部分参数。
lr (float)：初始学习率，可按需随着训练过程不断调整学习率。
momentum (float)：动量，通常设置为0.9，0.8。
dampening (float)：若采用 nesterov，dampening 必须为 0。
weight_decay (float)：权值衰减系数，即L2正则项的系数。
nesterov (bool)：bool，是否使用 NAG(Nesterov accelerated gradient)。

（2） torch.optim.Adagrad：

torch.optim.Adagrad(params, 
                    lr=0.01, 
                    lr_decay=0, 
                    weight_decay=0, 
                    initial_accumulator_value=0, 
                    eps=1e-10)

（3）torch.optim.RMSprop

 

torch.optim.RMSprop(params, 
                    lr=0.01, 
                    alpha=0.99, 
                    eps=1e-08, 
                    weight_decay=0, 
                    momentum=0, 
                    centered=False)

（4）torch.optim.Adadelta

torch.optim.Adadelta(params, 
                     lr=1.0, 
                     rho=0.9, 
                     eps=1e-06, 
                     weight_decay=0)

（5）torch.optim.Adam(AMSGrad)（实际中常用）

Adam是一种自适应学习率的优化方法，Adam利用梯度的一阶矩估计和二阶矩估计动态的调整学习率。Adam 结合了 RMSprop 和 Momentum，并进行了偏差修正，是非常常用的优化算法。

torch.optim.Adam(params, 
                 lr=0.001, 
                 betas=(0.9, 0.999), 
                 eps=1e-08, 
                 weight_decay=0, 
                 amsgrad=False)

（6）torch.optim.Adamax

torch.optim.Adamax(params, 
                   lr=0.002, 
                   betas=(0.9, 0.999), 
                   eps=1e-08, 
                   weight_decay=0)

（7）torch.optim.SparseAdam

torch.optim.SparseAdam(params, 
                       lr=0.001, 
                       betas=(0.9, 0.999), 
                       eps=1e-08)

（8） torch.optim.AdamW

torch.optim.AdamW(params, 
                  lr=0.001, 
                  betas=(0.9, 0.999), 
                  eps=1e-08, 
                  weight_decay=0.01, 
                  amsgrad=False)

（9） torch.optim.ASGD

torch.optim.ASGD(params, 
                 lr=0.01, 
                 lambd=0.0001, 
                 alpha=0.75, 
                 t0=1000000.0, 
                 weight_decay=0)

（10）torch.optim.LBFGS

torch.optim.LBFGS(params, lr=1, 
                  max_iter=20, 
                  max_eval=None, 
                  tolerance_grad=1e-07, 
                  tolerance_change=1e-09, 
                  history_size=100, 
                  line_search_fn=None)

（11）torch.optim.Rprop

torch.optim.Rprop(params, 
                  lr=0.01, 
                  etas=(0.5, 1.2), 
                  step_sizes=(1e-06, 50))

7、处理数据和训练模型的技巧

（1）预处理阶段：

1>中心化：所有数据减去均值，使得均值为0

2>标准化：方法一：除以标准差，使得分布接近高斯分布

                        方法二：按比例缩放到-1~1之间

3>PCA(主成分分析)：能够降低数据的维度

4>白噪声：与PCA一样，先将数据投影到一个特征空间，再每个维度除以特征值来标准化数据，使得数据呈（0,1）的多元高斯分布

（2）权重初始化

1>全0（不可取）

2>随机初始化：高斯随机化，均匀随机化 

3>稀疏初始化：（使用较少）

4>初始化偏置：（bias）

5>批标准化：通常在全连接层后面，非线性层前面（标准技术）

（3）防止过拟合：

一般采用全局权重L2正则化搭配Dropout

1>正则化：L2正则化使用较多（对权重过大的部分进行惩罚）

2>Dropout:训练网络时依概率P保留每个神经元

8、多层全连接层实现手写数字识别

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import torchvision
from torch.autograd import Variable
from torch.utils.data import DataLoader
import cv2

# 数据集加载
train_dataset = datasets.MNIST(
    root='./num/',
    train=True,
    transform=transforms.ToTensor(),
    download=True
)
test_dataset = datasets.MNIST(
    root='./num/',
    train=False,
    transform=transforms.ToTensor(),
    download=True
)

batch_size = 64

train_loader = torch.utils.data.DataLoader(
    dataset=train_dataset,
    batch_size=batch_size,
    shuffle=True
)

test_loader = torch.utils.data.DataLoader(
    dataset=test_dataset,
    batch_size=batch_size,
    shuffle=True
)

# 单批次数据预览
# 实现单张图片可视化
images, labels = next(iter(train_loader))
img = torchvision.utils.make_grid(images)

img = img.numpy().transpose(1, 2, 0)
std = [0.5, 0.5, 0.5]
mean = [0.5, 0.5, 0.5]
img = img * std + mean
print(labels)
cv2.imshow('win', img)
key_pressed = cv2.waitKey(0)


# 神经网络模块
class LeNet(nn.Module):
    def __init__(self, in_dim=None, n_hidden_1=None, n_hidden_2=None, out_dim=None):
        super(LeNet, self).__init__()
        self.flatten = nn.Flatten()
        self.layer1 = nn.Linear(in_dim, n_hidden_1)
        self.layer2 = nn.Linear(n_hidden_1, n_hidden_2)
        self.layer3 = nn.Linear(n_hidden_2, out_dim)

    def forward(self, x):
        x = self.flatten(x)
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        return x


# 训练模型
if torch.cuda.is_available():
    device = 'cuda'
else:
    device = "cpu"

net = LeNet(28 * 28, 300, 100, 10).to(device)

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(params=net.parameters(), lr=1e-3)

epoch = 1
if __name__ == '__main__':
    for epoch in range(epoch):
        sum_loss = 0.0
        for i, data in enumerate(train_loader):
            inputs, labels = data
            inputs, labels = Variable(inputs).to(device), Variable(labels).to(device)
            optimizer.zero_grad()  # 将梯度归零
            outputs = net(inputs)  # 将数据传入网络进行前向运算
            loss = criterion(outputs, labels)  # 得到损失函数
            loss.backward()  # 反向传播
            optimizer.step()  # 通过梯度做一步参数更新

            # print(loss)
            sum_loss += loss.item()
            if i % 100 == 99:
                print('[%d,%d] loss:%.03f' %
                      (epoch + 1, i + 1, sum_loss / 100))
                sum_loss = 0.0
    net.eval()  # 将模型变换为测试模式
    correct = 0
    total = 0
    for data_test in test_loader:
        images, labels = data_test
        images, labels = Variable(images).to(device), Variable(labels).to(device)
        output_test = net(images)
        _, predicted = torch.max(output_test, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum()
    print("correct1: ", correct)
    print("Test acc: {0}".format(correct.item() /
                                 len(test_dataset)))

 

 测试结果：90.47%正确率