softmax 分类器

softmax 分类器
两种常用的分类器之一。

1.从两个角度理解

（1）信息论中交叉熵

H(p,q)=−∑xp(x)log(q(x))=H(p)+DKL(p||q)H(p,q)=−∑xp(x)log(q(x))=H(p)+DKL(p||q)

p是指真实的分布，q是估计的分布。
式中H(p)是真实分布的熵，当给定分布，熵就确定；
DKL(p||q)DKL(p||q)是相对熵。
softmax分类器就是要最小化估计分类概率和真实分布之间的交叉熵。
交叉熵用于评估两个分布的相似度。

（2）概率的角度

softmax函数

P(yi|xi,w)=efyi∑jefjP(yi|xi,w)=efyi∑jefj

给定输入 xixi和参数w，分配给正确分类标签的归一化概率。

2. softmax在实际应用中的问题

softmax函数

P(yi|xi,w)=efyi∑jefjP(yi|xi,w)=efyi∑jefj

分子和分母都做指数运算，当数值很大的时候，会出现指数爆炸等问题。
常用的处理方法是分子分母同时乘以一个常数C，

efyi∑jefj=CefyiC∑jefj=efyi+logC∑jefj+logCefyi∑jefj=CefyiC∑jefj=efyi+logC∑jefj+logC

C通常取值为 −max(fj)−max(fj),使最大的值为0.

# python实现
 f -= np.max(f)
 p = np.exp(f)/np.sum(np.exp(f))

3. 一个简单的示例

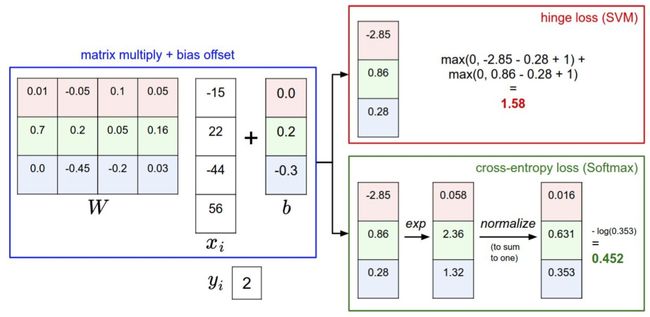
这里需要强调的是：最后的输出直接由权重上一层的输出+偏置*求得，并没有经过sigmoid函数。
这里的输出结果是[−2.85,0.86,0.28][−2.85,0.86,0.28]。

1) 先求efjefj,

[e−0.285,e0.86,e0.28]=[0.058,2.36,1.32][e−0.285,e0.86,e0.28]=[0.058,2.36,1.32]

2) 求 ∑jefj∑jefj

e−0.285+e0.86+e0.28=0.058+2.36+1.32=3.738e−0.285+e0.86+e0.28=0.058+2.36+1.32=3.738

3) 求输出概率

P(y1|x1,w)=efy1∑jefj=0.0583.738=0.016P(y1|x1,w)=efy1∑jefj=0.0583.738=0.016

P(y2|x1,w)=efy2∑jefj=2.363.738=0.631P(y2|x1,w)=efy2∑jefj=2.363.738=0.631

P(y3|x1,w)=efy3∑jefj=1.323.738=0.0353P(y3|x1,w)=efy3∑jefj=1.323.738=0.0353

softmax估算出每个类别的可能性。
给一个类别的打分为[1,−2,0][1,−2,0],softmax通过上述的计算，得到概率输出[0.7,0.04,0.26][0.7,0.04,0.26]。
进一步考虑正则项的影响，假设惩罚使得得分的输出变为原来的1212，即[1,−2,0][1,−2,0]=>[0.5,−1,0][0.5,−1,0]时，最终得到的输出为[0.55,0.12,0.33][0.55,0.12,0.33].
softmax分类器会使正确的分类获得更大的概率，使错误的分类得到更小的概率。

（1）CS231n课程笔记翻译：线性分类笔记（下）
https://zhuanlan.zhihu.com/p/21102293?refer=intelligentunit
（2）cs231n-assignment1-SVM/Softmax/two-layer-nets梯度求解
https://blog.csdn.net/pjia_1008/article/details/66972060
（3）CS231n课程学习笔记（三）——Softmax分类器的实现
https://blog.csdn.net/stalbo/article/details/79379078
（4）斯坦福大学深度学习公开课cs231n学习笔记（9）softmax分类和神经网络分类代码实现
https://blog.csdn.net/piaoxuezhong/article/details/78818572

转载于:https://www.cnblogs.com/siucaan/p/9623144.html