ARIMA时间序列分析——（一）数据平稳性检验

时间序列，指的是按时间顺序索引的一系列数据点，是面板数据的一种，属于一维面板数据。

时间序列分析包括用于分析时间序列数据以及提取有意义的统计数据和数据其他特征的方法。

ARIMA模型构建流程：

        1.判断模型的平稳度

        2.差分法对非平稳时间序列进行平稳化处理

        3.模型定阶

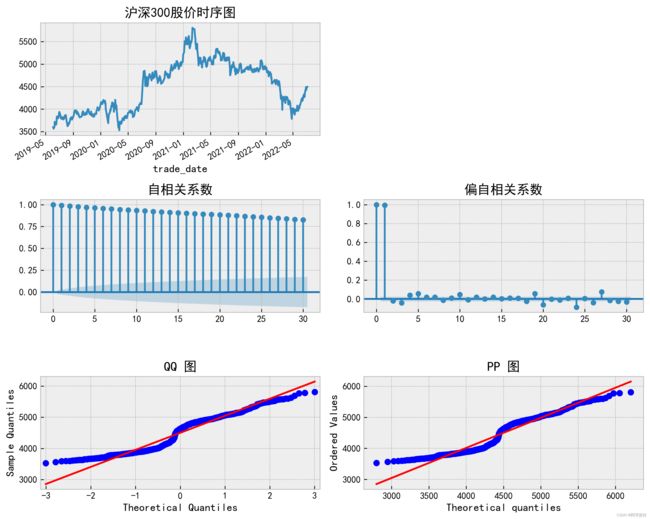
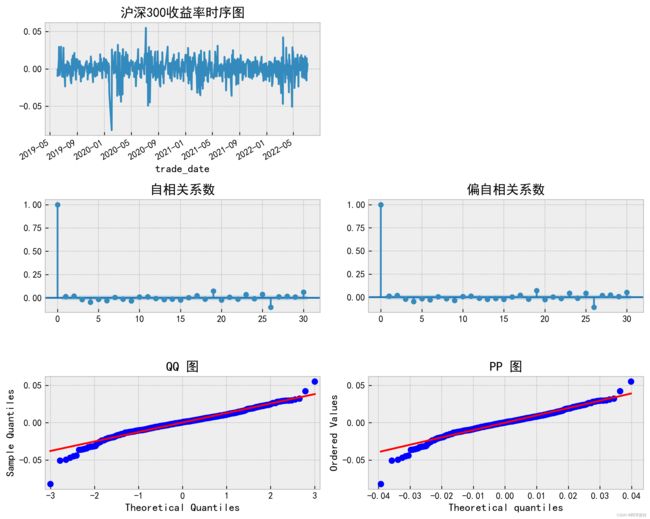
本文主要介绍构建模型流程的第一步，即判断模型的平稳度，以近三年的沪深300指数为例：

判断时间序列是否为平稳序列的方式有两种，一是通过单位根检验（如DF、ADF、PP方法等

）； 二是通过观察时间序列的自相关（Autocorrelation Coefficient，ACF）和偏自相关（Partial

Autocorrelation Coefficient，PACF）函数图，对于平稳时间序列而言，其自相关或偏自相关系数

一般会在某一阶后变为迅速降低为0左右，而非平稳的时间序列的自相关系数一般则是缓慢下降

（PS：ACF与PACF在平稳序列中可作为模型定阶的参考依据）。

以近三年的沪深300指数为例：

#%% 导入需要的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
%matplotlib inline 

#正常显示画图时出现的中文和负号
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False

#### 获取数据，从tushare上获取沪深300指数为例
import tushare as ts
token= "输入你的token号"   # 网站 https://tushare.pro/
pro=ts.pro_api(token)

def get_data(code,n=250*3):
    df=pro.index_daily(ts_code=code)
    #将日期设置为索引
    df.index=pd.to_datetime(df.trade_date)
    #最近n日价格走势
    df=df.sort_index()[-n:]
    #只保留收盘价数据
    del df[df.index.name]
    return df.close

df=get_data('000300.SH')


#### 引入statsmodels和scipy.stats用于画QQ和PP图
import scipy.stats as scs
import statsmodels.api as sm
def ts_plot(data, lags=None,title=''):
    if not isinstance(data, pd.Series):   
        data = pd.Series(data)
    with plt.style.context('bmh'):    
        fig = plt.figure(figsize=(10, 8),dpi=300)
        layout = (3, 2)
        ts_ax = plt.subplot2grid(layout, (0, 0))

        acf_ax = plt.subplot2grid(layout, (1, 0))
        pacf_ax = plt.subplot2grid(layout, (1, 1))
        qq_ax = plt.subplot2grid(layout, (2, 0))
        pp_ax = plt.subplot2grid(layout, (2, 1))

        data.plot(ax=ts_ax)
        ts_ax.set_title(title+'时序图')
        smt.graphics.plot_acf(data, lags=lags, ax=acf_ax, alpha=0.5)
        acf_ax.set_title('自相关系数')
        smt.graphics.plot_pacf(data, lags=lags, ax=pacf_ax, alpha=0.5)
        pacf_ax.set_title('偏自相关系数')
        sm.qqplot(data, line='s', ax=qq_ax)
        qq_ax.set_title('QQ 图')        
        scs.probplot(data, sparams=(data.mean(), data.std()), plot=pp_ax)
        pp_ax.set_title('PP 图') 
        plt.tight_layout()
    return



#### 沪深300近三年价格与收益率数据
data=pd.DataFrame(df,columns=['close'])
#对数收益率
data['logret']=np.log(data.close/data.close.shift(1))
#普通收益率
data['ret']=data.close/data.close.shift(1)-1
data=data.dropna()

#### 沪深300股价与收益率的平稳性判断
#法一：单位根检验（利用ADF检验）
print(sm.tsa.stattools.adfuller(data.close)) # 利用statsmodels模块进行ADF检验

from arch.unitroot import ADF # 利用arch.unitroot模块进行ADF检验
import ADF
ADF(data.close)
ADF(data.logret)              # 两种模块计算得到的结果一致


#法二：观察时序图
ts_plot(data.close,lags=30,title='沪深300股价')
#沪深300收益率,对数收益率与算术收益率差异不是很大
ts_plot(data.logret,lags=30,title='沪深300收益率')

通过法一得到的结果：

股价ADF结果如下

(-1.9036374544321113, 0.33035187700494084, 0, 748, {'1%': -3.43912257105195, '5%': -2.8654117005229844, '10%': -2.568831705010152}, 7957.254181584909)

收益率ADF结果如下

(-26.93729155995837, 0.0, 0, 748, {'1%': -3.43912257105195, '5%': -2.8654117005229844, '10%': -2.568831705010152}, -4290.046359288771)

第一个值：表示Test Statistic ， 即T值，表示T统计量；第二个值：p-value，即p值，表示T统计量

对应的概率值；大括号中的值，分别表示1%， 5%， 10% 的三个level以及其对应的p-value值，p

值大于5%，则可以认为该数据是不平稳的。通过ADF检验得到股价是不平稳序列，收益率是平稳

序列。

 

通过法二得到的结果：

股价 

收益率：

因此，通过判断自相关系数以及偏自相关系数能够得到，股价为非平稳序列，收益率为平稳序

列。

参考文献：

【Python量化基础】时间序列的自相关性与平稳性

Python实现对数据的ADF检验 - 知乎

张建海, 张棋, 许德合, 等. ARIMA-LSTM 组合模型在基于 SPI 干旱预测中的应用——以青海省为例[J]. 干旱区地理, 2020, 43(4): 1004G1013.

https://en.wikipedia.org/wiki/Time_series