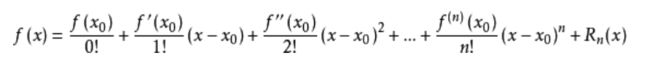Side Window Filtering
刚开始看到这篇论文的时候,我就很感兴趣想去复现一把看看效果。
这篇论文是今年 CVPR oral 且不是深度学习方向的,其核心贡献点就是:
不管原来的滤波器保不保边,运用了side-window思想之后,都可以让它变成保边滤波!
于是利用业余时间,参考作者开源的matlab代码,我用C++实现了一下Side-window
盒子滤波,其他滤波器有时间再试下,下面是github的链接,读者可以去跑下代码看看效果玩下,
从实验结果上看我觉得算是复现了论文的效果:
https://github.com/Ldpe2G/ArmNeonOptimization/tree/master/sideWindowBoxFilter
我们来看下复现论文的效果,对于一张普通图片,经典的盒子滤波和side-window
盒子滤波的效果对比:
从滤波结果对比上可以看到,经典的盒子滤波随着对同一张图片反复应用盒子滤波的迭代次数
的增加,视觉效果是越来越模糊,到了30次迭代的时候已经糊的没法看了,但是Side-window
盒子滤波即使迭代了30次,对于边缘的保持还很好,和原图基本看不出大的区别,就是边缘细节
有些丢失。然后对原图加上椒盐噪声,再对比下滤波效果:
从滤波结果对比上可以看到,经典的盒子滤波到了10次迭代的时候,虽然椒盐噪声已经很好
的消除了,但是图片也变得很模糊,边缘都细节都丢失了,但是Side-window盒子滤波却能
很好的消除椒盐噪声的同时,对于边缘的保持还很好,基本上算是还原了原图。
下面从我的理解上去简单解读下这篇论文的核心思想,还有我在复现过程中的一些实现
细节介绍。目前的经典滤波算法基本都是,以某个像素点为中心,按照滤波半径,把这个
包括像素点和其领域加权组合得到输出,一般公式如下:
Ω是以像素点 i 为中心的滤波窗口,w是滤波权值,q是原图像素值,I'是输出结果。
但是这样以一个像素为中心去滤波会的问题在于,如果一个像素点处在边缘位置
(这里的边缘不是指图片的大小边界,而是指图像中物体的边缘)的话,以像素为
中心的滤波会导致滤波结果的边缘部分变模糊。具体是为什么,论文中给出了分析过程。
首先来看下,论文中的一张图:
文中提到为了分析方便只讨论3种典型的边缘,分别是图中的
(a)阶梯状边缘、(b)斜坡状边缘和(c)屋顶状边缘。论文中也给出了这3三种边缘的形象展示:
然后文中采用了泰勒展开去分析,首先假定,图像上(x, y)坐标点的像素值为g(x, y),对于
图中展示的情况来看,函数 g(x, y)是连续但不可导的。对于(a)阶梯状边缘的 'a' (蓝色方框那个店)
点来说,文中定义 'a-' 和 'a+' 来分别表示 'a' 点左极限 (x - ε, y),和右极限 (x + ε, y)。且 ε > 0。
很明显从图中可以看出来 g(x - ε, y) ≠ g(x + ε, y) 且/或(文中的用词是"and (or)")
g'(x - ε, y) ≠ g'(x + ε, y),导数也不等由于边缘部分的跳跃。因此对于这两块区域的泰勒展开也是
不一样的,首先来看下泰勒展开的一般公式:
“泰勒公式是将一个在 x=x0 处具有n阶导数的函数 f(x) 利用关于 (x - x0) 的n次多项式来
逼近函数的方法。”----百度百科
根据文中的分析,这里设定 f(x) = g(x - 2ε, y),x0 = x - ε,则根据泰勒展开公式:
g(x - 2ε, y) ≈ f(x0) + f'(x0)(x - x0)
= g(x - ε, y) + g'(x - ε, y)(x - 2ε - (x - ε))
= g(x - ε, y) + g'(x - ε, y)(- ε)
同理,设 f(x) = g(x + 2ε, y),x0 = x + ε,则泰勒展开得:
g(x + 2ε, y) ≈ f(x0) + f'(x0)(x - x0)
= g(x + ε, y) + g'(x + ε, y)(x + 2ε - (x + ε))
= g(x + ε, y) + g'(x + ε, y)ε
所以从两边的泰勒展开式可以得出结论,对于 'a-' 区域的滤波估计肯定是来自区域 'a' 的左边,
而对于 'a-' 估计是来自于 'a' 的右边,然后类比分析区域 'b','c' 和 'd' 都可以得到类似的结论。
因此分析得到的结论是,如果一个像素点处于图像中的边缘位置,那么滤波的时候就应该把
滤波器的边缘和该像素点对齐,而不是把滤波器的中心和该像素点对齐。受该发现的启发,
文中提出了一个新的保边滤波策略,就是把每个滤波像素点都当成是潜在的边缘点,然后
对于每个待滤波的像素点,生成几种不同的滤波子窗口,然后把这些滤波窗口的边缘或者
角点位置和该像素点对齐,然后滤波得到结果,最后根据把这些子窗口的滤波之后的最佳
重构结果作为最终的滤波结果。以上就是side window 滤波的思想。
然后文中提出了8个方向的滤波窗口,分别是上、下,左、右、左上、右上、左下和右下。
还有对于窗口的分析,最后就可以得到side window filter的核心算法流程:
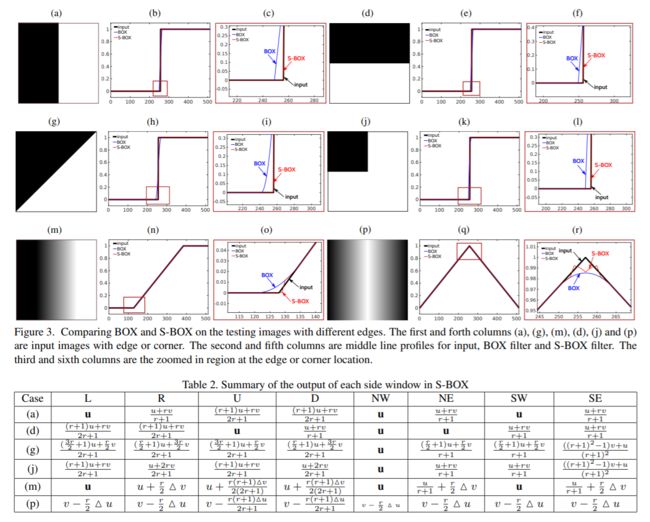
然后论文中又详细分析了 box filter 和 side window box filter 对于上面提到的三种经典
边缘的滤波之后的保留情况。文中给出分析的图表如下:
总的来说结论就是 side window box filter 对于阶梯和斜坡状的边缘都能完整的保留,
而对于屋顶状边缘虽然不能完整的保留边缘,但是也比经典的盒子滤波要好很多。
在复现过程中,本来一开始是想对文中提到的8种side window去分别写对应的盒子滤波的,
因为盒子滤波有个经典的优化思路,可以让运行时间不受滤波半径的影响,
具体可以参考我之前写得一篇博客:
移动端arm cpu优化学习笔记----一步步优化盒子滤波(Box Filter)
后来仔细想了下,这8个side window其实也就是边界处理不同,核心运算逻辑都是一致的,
最后就是抽象成一个函数,对于不同的side window传不同的边界参数,
就不需要每个窗口写一个函数了,具体可以看看github上的代码。
最后看看一组结果,看看在迭代10次的情况下,经典box filter 和 side window box filter的结果对比:
熊猫宝宝原图
滤波结果, box filter, iteration = 10
滤波结果, side window box filter, iteration = 10
熊猫宝宝原图+椒盐噪声
去噪结果, box filter, iteration = 10
去噪结果, side window box filter, iteration = 10
相关资料:
CVPR2019 Oral论文 #5176 Side Window Filtering介绍
Sub-window Box Filter论文介绍