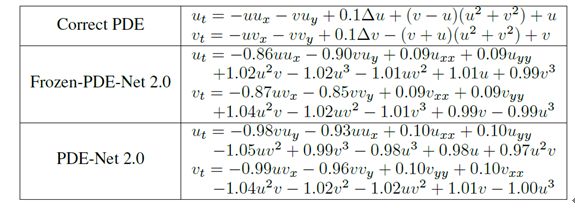董彬教授：用深度神经网络学习偏微分方程及其数值求解的离散格式

2019年10月31日下午，在北京智源大会的“人工智能的数理基础专题论坛”上，北京大学副教授、智源学者董彬做了题为《Learning and Learning to Solve PDEs》的主题演讲（编者注：PDE，Partial Differential Equation，偏微分方程）。早在加州大学圣地亚哥分校（UCSD）攻读博士后期间，董彬便在图像反问题领域做了一系列开创性的研究，他同合作者一起建立了小波框架（Wavelet Frames）和变分模型（Variational Models）及偏微分方程（PDEs）的深层联系。

这一系列工作的意义在于[1]：1）赋予PDE方法稀疏逼近的解释，这是对PDE方法一个新的诠释；2）严格证明了离散化后的小波框架模型和迭代算法与对应的变分模型和PDE 模型的一致性，完善了这方面的理论工作；3）为小波框架方法赋予了几何解释，使得我们可以设计出几何意义更强的自适应小波框架算法，另一方面，小波框架模型和迭代算法也对应了一些全新的变分和PDE模型，从而进一步推动了图象反问题中PDE方法的发展；4）为探索PDE和深度学习的联系、寻求机理与数据融合建模与计算提供了一定的理论基础。

 

从中我们可以看到董彬做研究的一个特点，就是将数学中的不同分支融合，包括桥接小波框架理论、变分技术和非线性PDE，将稀疏逼近与统计学和机器学习相结合。本次讲座，董彬给我们介绍了他最近的两个核心工作成果：第一，如何结合深层神经网络和PDE数值解，从观测数据反推出数据背后未知的PDE模型。第二，如何使用人工智能的重要分支--强化学习，学习数值求解守恒律偏微分方程的离散格式，尤其是在解的非光滑部分寻求更佳的数值逼近。

文章整理：钱小鹅

编辑：王炜强

01

 PDE-Net 2.0:

LearningPDEs from Data

微分方程，特别是偏微分方程，可以用来描述一个给定系统的基本物理定律，因此在许多学科中扮演着重要的角色。传统上，偏微分方程是基于数学或物理原理推导而成的，例如从量子力学中的薛定谔方程到分子动力学模型，从玻尔兹曼方程到Navier-Stokes方程等。然而，许多领域（如神经科学、金融学、生物科学等）中的复杂系统背后的机制仍然普遍不清楚，这些系统的控制方程通常通过经验公式获得。近二十年来，随着传感器、计算能力和数据存储技术的飞速发展，大量的数据可以很容易地被收集、存储和处理。如此大量的数据为数据驱动的机理/定律探索提供了新的方法和手段。因此，很多人可能会问一个非常有趣问题：我们是否可以从观测（或者高精度数值计算）得到的复杂动态数据出发，利用计算的手段，学习出背后的驱动PDE模型？

 

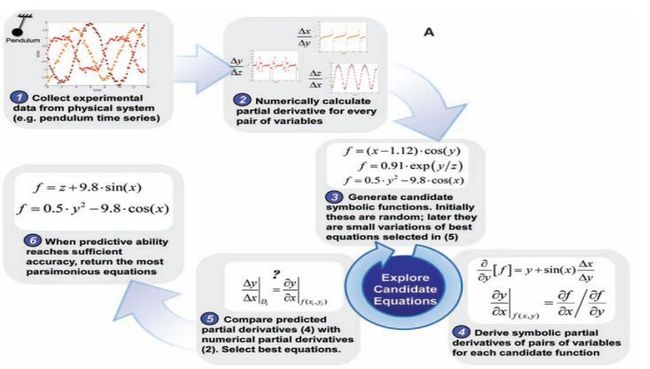
最早尝试使用数据来驱动发现隐藏物理定律可以追溯到2007年 Josh Bongard 和Hod Lipson的工作，其主要思想是将实验数据的数值微分与候选函数的解析导数进行比较，并将符号回归和进化算法应用于非线性动力系统。在计算机视觉领域，北京大学林宙辰团队也提出利用PDE控制的框架，对PDE的待定系数进行回归，从数据中去学习图像处理所需的PDE模型。当PDE的非线性响应函数的形式已知时，Maziar Raissi 和 George Em Karniadakis提出了一种利用高斯过程在两个连续时间步长之间引入正则性来学习未知标量参数的框架。       

  

2016年，Steven LBrunton等人贡献了另外一种方法：非线性动力学稀疏辨识（SINDy）。SINDy的核心思想是首先构造一个由简单函数和偏导数组成的线性字典，这些函数和偏导数都可能出现在方程中；然后，利用稀疏性从字典中选择能够最准确地拟合数据的函数形式。2017年，Emmanuel de Bezenac等人将深度学习中的神经网络引入其中，用于研究海面温度预报问题。Bezenac首先假设上述问题的物理模型是一个对流扩散方程，根据方程的通解设计了一个特殊的神经网络。与传统的数值方法相比，该方法在精度和计算效率上都有较大的提高。

 

我们看到，很多科研工作者已经在积极的寻找数据驱动PDE建模、从得出的PDE再探索物理规律的方法，但是目前的方法仍然存在一些弊端：

• 一般情况下（除非先验知识充分），我们首先需要建立一个足够大的字典用于搜索合适的PDE模型，但是当模型变量较多时，这可能导致较高的内存和计算成本；

•  在寻找合适的PDE模型的时候，我们要反复求解当前时刻的PDE模型，跟观测数据进行比对，计算出误差用于修正对PDE模型的估计。现有绝大多数算法在求解PDE模型时候都固定某些数值格式，这对PDE模型本身的估计未必是最佳的做法。

图1 给定部分约束条件，使用数据驱动得出偏微分方程的简单实例过程

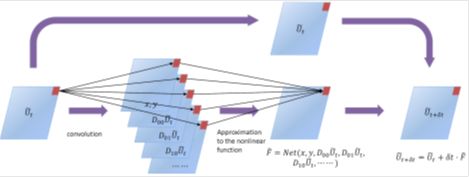
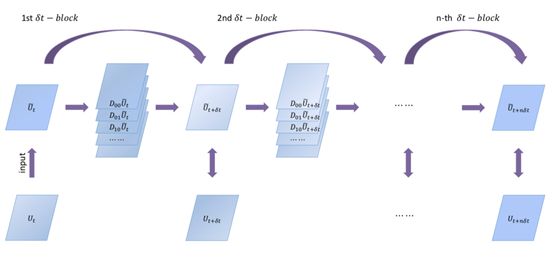
针对上述问题，董彬团队在2018、2019年先后提出了一款将神经网络和数值PDE融合的反问题模型，PDE-Net[2,3]，该网络可以从观测到的复杂动态数据中挖掘出隐藏的偏微分方程模型。我们不妨假设PDE格式如下：

PDE-Net通过在时间上使用前向欧拉格式，在空间上使用有限差分格式对上述PDE进行离散化而设计的一个前馈网络。前向欧拉格式（时间离散也可以采用其它格式）的引入使得网络与ResNet类似，有限差分部分引入的卷积核将会通过训练得到，非线性响应函数F可以通过一个回归网络[2]或用一个符号网络SymNet来逼近[3]，该网络和卷积核的所有参数都会从数据中联合学习到。其中，使用符号网络SymNet的PDE-Net[3]很好的解决了当我们对模型的动力学机理仅有少量的先验知识时（无需事先假定了解方程是双曲抑或抛物型非线性偏微分方程），仍然可以从数据中挖掘出模型。此外，在训练过程中，求解正问题所用的格式也是根据数据动态变化的，这一方面能够更好的辅助反问题的求解，即得到更加精确的PDE模型，另一方面也使得训练好的PDE-Net对任意给定初始条件都能进行较为长期的精确预测。

那么董彬团队是如何设计这个网络的呢？首先我们先引入一个“先验知识”：

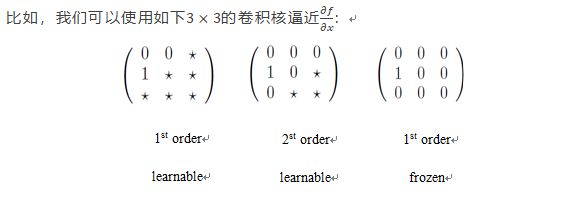
一个阶的微分算子，可以用一个有阶求和规则的滤波器来近似，我们甚至可以得到任何一个对于给定的高阶微分算子对应的滤波器的高阶近似。

因此，在一个PDE-Net中，对于一个给定带有约束条件的的滤波器，其对应的矩阵为：

其中：

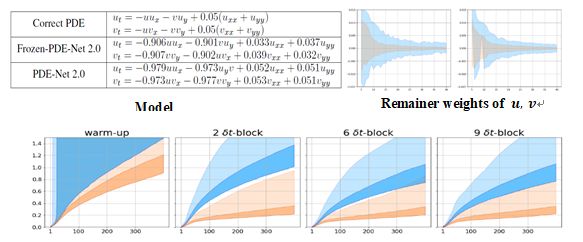
图4  Burger’s equation

图5：Burger’s + reaction

02

Learningto Discretize

to Solve PDEs from data

使用深度学习的神经网络，我们不光可以解决Burgers方程，还可以处理更复杂的系统，感兴趣的读者可以阅读董彬相关的论文继续深入探索。讲到这里，很多读者会问：我们可以使用数据寻找到最能表达这些数据背后规律的方程，那么我们是否也可以使用数据寻找更好的求解方程呢？答案是肯定的，董彬也在报告中做了精彩的讲述。他提到，使用机器学习方法求解PDE，在计算数学中是一个新兴的领域。这一新兴领域主要关心的问题在于如何解决高维的问题和更好的处理间断，近期也有很多值得关注的重要进展。目前这些工作使用的方法属于监督学习（SL），董彬团队在最新的论文中将强化学习（RL）也引入其中，展示了如何将迭代算法和马尔可夫决策过程（Markov Decision Process, MDP）建立联系，从精确解中学习求解守恒律方程的数值方法。

图6 神经网络及偏微分方程数值解目前的发展状况总览

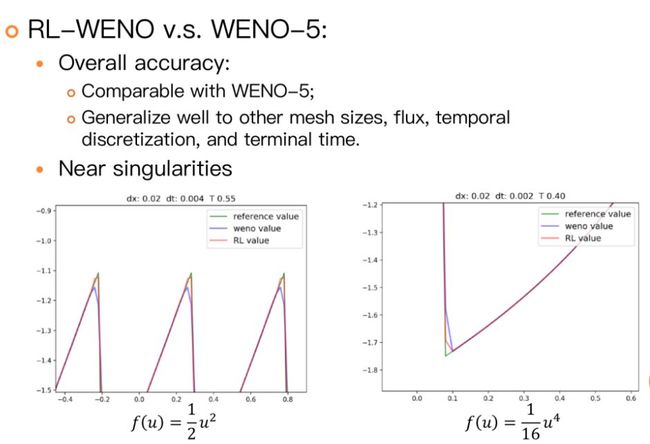
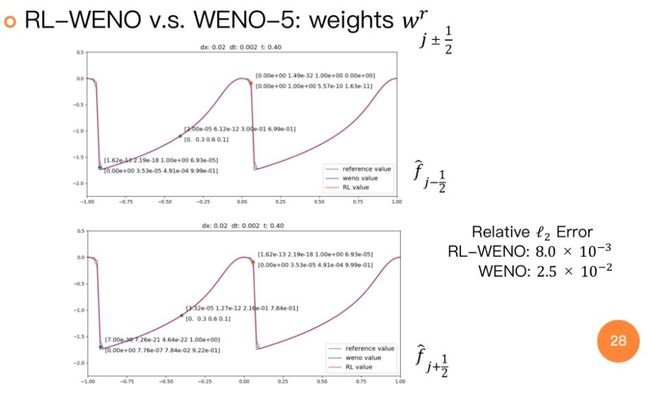
那么，为什么要将RL与学习PDE的离散格式联系在一起，这样做会有怎样的好处呢？首先，我们可以把含时PDE的数值离散看成是一个动态决策过程，其中决策部分是由我们来完成的,手动设计出的数值格式。如果要从精确解去学习（更优的）数值格式，那么PDE数值离散可以被很自然的看成是一个决策过程，伴随合适的时间离散，该过程就可以很自然的被视作一个MDP，再利用RL的技术去对决策进行优化。其次，传统的数值格式大多是“贪心”（Greedy）的，很难保证数值格式在长时间演化中的性能，尤其是对解在间断周围的处理，大多采取较为保守的方式，而这些反而是RL的优势所在。董彬团队在2019年的论文[4]中从一维标量守恒律方程出发，提出将WENO算法视作马尔可夫决策过程（MDP）并用将其设计转化为RL问题来优化。新的求解器（RL-WENO）总体性能和WENO-5相仿，但在间断处明显优于WENO，且RL-WENO在间断处选择的模板明显不同于WENO。将数值算法（可以是PDE求解算法，也可以是其它科学计算中的迭代算法）视作MDP并用RL去训练的这一做法，除了上述的几个好处，[4]还指出，RL的算法框架自然具备了元学习的优点，使得训练出的算法有更好的泛化能力。从这个角度看，RL和科学计算的很多算法可以很好的融合在一起，为机器学习与科学计算的融合提供了一个崭新的思路。更深入的了解，感兴趣的读者可以继续研究原论文及代码。

图7 RL-WENO与WENO-5的数值解进行比较，从图中我们可以看出在解的震荡部分RL-WENO离散格式的精度更高

03

结语

从21世纪初开始，随着科技的迅速发展，尤其是计算机的发展，我们进入了一个数据爆炸的时代，高维多源异构数据的处理和分析也越来越受到学术和工业界的重视。数据的迅速增长和计算能力的飞速提升，也使得人工智能在最近几年发展迅猛，其中最核心的技术之一就是深度学习。然而深度学习的模型复杂，模型设计很多时候是基于经验，缺乏系统的理论指导。此外，深度学习模型缺乏透明度和足够的可解释性，从而在一定程度上限制了它在严肃科学领域的应用。针对上述问题，董彬团队基于以往的理论研究（小波与PDE方法之间的联系），将计算数学与深度学习相结合，提出数值微分方程与深度学习和强化学习融合的思想，针对PDE的正反问题和图像反问题，为深层神经网络构架设计提供指导，并在该指导思想下设计了全新的、具有一定可解释性的模型与算法。

机器学习与科学计算的融合，是一个新兴的科研领域，在这个新兴的领域中，仍然有很多很有意思的问题值得我们继续探索：基于大数据的机器学习作为一类新的计算方法，是否可以解决应用数学中的瓶颈问题；应用数学能否给机器学习（特别是深度学习）提供系统的理论指导。这些问题，等待着我们继续努力研究，有兴趣的读者亦可以加入智源的数理基础群进行进一步的讨论。

 

 

参考文献： 

[1]北大教授董彬：从学子的初等函数开始，以师者的小波函数延续，https://baijiahao.baidu.com/s?id=1589193349638531472&wfr=spider&for=pc

[2]Zichao Long, Yiping Lu, Xianzhong Ma and BinDong, PDE-Net: Learning PDEsfrom Data, Thirty-fifth International Conference on MachineLearning (ICML), 2018 (arXiv:1710.09668).

Codes, Supplementary Materials.

[3]Zichao Long, Yiping Lu and Bin Dong, PDE-Net 2.0: LearningPDEs from Data with A Numeric-Symbolic Hybrid Deep Network, Journal ofComputational Physics, 399, 108925,2019 (arXiv:1812.04426). Codes.

[4]Yufei Wang, Ziju Shen, Zichao Long and Bin Dong, Learning to Discretize:Solving 1D Scalar Conservation Laws via Deep Reinforcement Learning, arXiv:1905.11079, 2019. Codes.

看完文章不过瘾，还想和人讨论讨论？

智源AI社群欢迎你：

 

- 往期文章 -