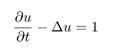MATLAB中pdetool工具求解泊松方程和Laplace方程
MATLAB中pdetool工具求解泊松方程和Laplace方程
求解步骤及主要函数:
1、问题定义
2、创建具有单个因变量的PDE模型, createpde()
3、创建几何结构并将其追加到PDE模型中,geometryFromEdges()
4、使用边界条件,pdegplot()
5、指定PDE系数
6、指定初始条件,setInitialConditions()
7、生成网格,pdemesh()
8、生成时间离散化
9、求解数值解,solvepde()
10、绘图解的图形,pdeplot()
R1 = [3;4;-1;1;1;-1;-1;-1;1;1];
C1 = [1;0;0;0.4];
C1 = [C1;zeros(length(R1) - length(C1),1)];
gd = [R1,C1];
sf = ‘R1+C1’;
ns = char(‘R1’,‘C1’)’;
g = decsg(gd,sf,ns);
numberOfPDE = 1;
pdem = createpde(numberOfPDE);
geometryFromEdges(pdem,g);
figure
pdegplot(pdem,‘edgeLabels’,‘on’,‘subdomainLabels’,‘on’)
axis([-1.1 1.1 -1.1 1.1]);
axis equal
title ‘Geometry With Edge and Subdomain Labels’
applyBoundaryCondition(pdem,‘Edge’,(1:4),‘u’,0);
specifyCoefficients(pdem,‘m’,0, ‘d’,1, ‘c’,1, ‘a’,0,‘f’,1);
setInitialConditions(pdem,0);
setInitialConditions(pdem,1,‘face’,2);
msh = generateMesh(pdem);
figure;
pdemesh(pdem);
axis equal
nframes = 20;
tlist = linspace(0,0.1,nframes);
pdem.SolverOptions.ReportStatistics =‘on’;
result = solvepde(pdem,tlist);
u1 = result.NodalSolution;
figure
umax = max(max(u1));
umin = min(min(u1));
for j = 1:nframes,
pdeplot(pdem,‘xydata’,u1(:,j),‘zdata’,u1(:,j));
caxis([umin umax]);
axis([-1 1 -1 1 0 1]);
Mv(j) = getframe;
end
movie(Mv,1);