Less is More_ Pay Less Attention in Vision Transformers论文解读

与Fast Vision Transformers with HiLo Attention论文解读)

前言

  这篇文章介绍两篇论文，一篇是LiT,另一篇是它的改进版本LiTv2。LiT的创新点在于两个地方。第一点在4阶段的层次化vision transformer结构中使用两个线性层来取代一个阶段的多头自注意力。4个阶段前两个阶段都是mlp层。减少了计算量。第二点在于使用了Deformable Convolution来做patch merging.
  改进版本LiTv2的创新点在于将原始版本的transformer块换成了文中提出的HiLo Attention块，这个attention块通过池化把特征图分为低频做自注意力提取低频全局特征，再拿原始特征图做自注意力提取局部特征，最后拼接两者得到输出。
论文地址：
LiT论文PDF地址
LiTv2论文PDF地址
代码地址：
LiT github代码地址
LiTv2 github代码地址

1. LiT

  下图是LiT的整体架构图。

MLP取代MSA

  可以看到LiT是4阶段，层次化的transformer。作者试图论证多头自注意力只要头数足够，就可以模拟逼近任何卷积层。单头注意力则与FC层比较类似。作者得出结论，既然这样可以尝试用卷积层去模拟自注意力层。当然作者也提示两者在实际应用上肯定是不等的。
最后作者使用了mlp层取代了前两个阶段，保留了后两个阶段的MSA.

class Mlp(nn.Module):
    """ Multilayer perceptron."""

    def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
        super().__init__()
        out_features = out_features or in_features
        hidden_features = hidden_features or in_features
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)

    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.drop(x)
        x = self.fc2(x)
        x = self.drop(x)
        return x

从代码可以看到mlp使用了两个线性层来代替MSA。Linear->GELU->Linear

DTM

DTM(deformable token merging)。作者直接调用了封装好的形变卷积模块。这里按我的理解是形变卷积给采样点加了一个可学习参数，他会让采样点的位置发生偏移，随着学习到相关信息，偏移会转向信息集中的地方。


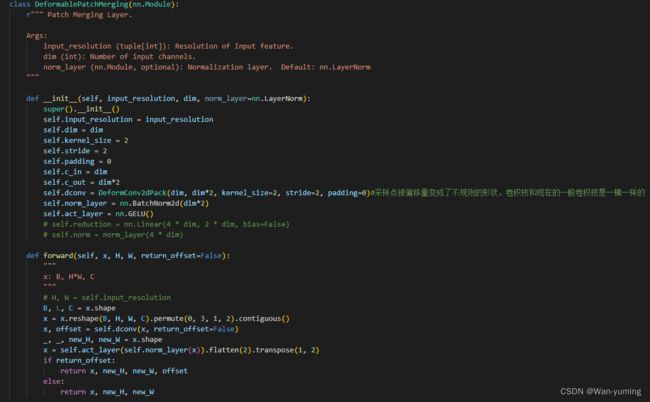
  上面第一幅图代表了标准的3x3卷积，但是加上偏移量以后，采样点有可能出现不同方向的偏移，如第二张图。而第三张和第四张代表偏移时发生的特例。在本文中，第一阶段的patch embed用的是传统的卷积实现，剩余阶段的patch emerging，在patch逐渐变大的过程中是使用DTM实现的。作者为了展示DTM的效果，将可视化效果展示在下图。下图绿框代表卷积核，红色代表采样点。可以发现，确实可学习偏移将采样点分布在更加符合图像特征的地方。

上述即为LiT的两个创新点，实际上可说的点还是挺少的。而LiTv2在继承DTM和前两个MLP替代transformer阶段之后，对attention块进行了改进，提出了一种HiLo Attention的结构。

2. LiTv2

  下图是LiTv2的整体架构。与Lit相比主要改动在于Transformer模块。现在我们详细考察一下本文提出的HiLo Attention。

  下图为HiLo attention模块的架构图。我们先来介绍一下作者的理论。作者认为原始输入图像中含有丰富的频率，并且不同频率扮演不同的角色。类如高频信息含有丰富的局部细节特征。低频信息含有丰富的全局特征信息。传统的MSA直接对输入特征图做自注意力使得不同频率的信息混在一起。所以作者想从不同频率入手分别处理高频和低频信息。作者分了两条路径，分别是原图像大小和平均池化后的图像大小，作者认为分别从两者入手可以对高频/低频信息通过自注意力进行编码，提取。
  从下图可以看出，上面的路径显然是高频处理路径，下面的是低频处理路径。作者为高频和低频分配不同数量的头。两者的和是原先设定的头的数量。具体分配给低频αN个头，分配给高频(1-α)N个头。N是设定的总的头的数量。例如N取8，α取0.75.那么低频可以分到6个头，高频可以分到2个头。至于α的取值，作者承认对于不同任务，适宜的α取值也不一样，需要手动调整。既然头被分割了，那代表着原输入特征图的维度也需要分割。例如输入特征图维度取64，那么按上面举例的取值，高频特征图的维度需要取16，低频特征图的维度需要取48，以方便处理。但是分割维度并不是直接分割，将64按16和48分开会让高频和低频图损失对方拥有的信息，所以作者通过线性层将维度降低到高频和低频的维度，这样可以减少分割维度所造成的信息损失。
  高频图像采用窗口划分来做自注意力，而低频图像需要先对高频图像做kernel size=window size,stride=window sdize的平均池化才能获取。接着就是上面所提的划分头和划分维度。接下来就是attention的计算过程了。高频attention我们称之为Hi-Fi.qkv就是直接通过线性层来取，qkv的shape（B, hw, n_head, wsws, head_dim），ws是window_size,我们可以只看（wsws, head_dim）,qk^T 的shape（wsws，wsws），再乘以v,shape变为（wsws, head_dim）。通过窗口划分减小了计算量，提高了计算效率。

接下来看看Lo-Fi也就是低分辨率的attention过程。详见下方代码def lofi(self, x)，这里需要注意，低频attention的q用的是在高频图取的q，(B,n_head,HW,head_dim)，K与V在低频图取，(B,n_head,HW/SS,head_dim)，这里n_head应该是低频图的分配的头的数量。这样计算下来，qk^T的shape变为（B,n_head，HW，HW/SS），再乘以v后shape变为（B,n_head，HW，head_dim），这样下来可以发现不需要插值，只需要简单的reshape（B，H,W,C_LOFI）就能与高频图concat。并且concat后，维度加起来正好是原输入特征图的维度。这就是HiLo Attention的过程。

class HiLo(nn.Module):
    """
    HiLo Attention

    Link: https://arxiv.org/abs/2205.13213
    """
    def __init__(self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0., window_size=2, alpha=0.5):
        super().__init__()
        assert dim % num_heads == 0, f"dim {dim} should be divided by num_heads {num_heads}."
        head_dim = int(dim/num_heads)

        self.dim = dim
        # self-attention heads in Lo-Fi
        self.l_heads = int(num_heads * alpha)
        # token dimension in Lo-Fi
        self.l_dim = self.l_heads * head_dim

        # self-attention heads in Hi-Fi
        self.h_heads = num_heads - self.l_heads
        # token dimension in Hi-Fi
        self.h_dim = self.h_heads * head_dim

        # local window size. The `s` in our paper.
        self.ws = window_size

        if self.ws == 1:
            # ws == 1 is equal to a standard multi-head self-attention
            self.h_heads = 0
            self.h_dim = 0
            self.l_heads = num_heads
            self.l_dim = dim

        self.scale = qk_scale or head_dim ** -0.5

        # Low frequence attention (Lo-Fi)
        if self.l_heads > 0:
            if self.ws != 1:
                self.sr = nn.AvgPool2d(kernel_size=window_size, stride=window_size)
            self.l_q = nn.Linear(self.dim, self.l_dim, bias=qkv_bias)
            self.l_kv = nn.Linear(self.dim, self.l_dim * 2, bias=qkv_bias)
            self.l_proj = nn.Linear(self.l_dim, self.l_dim)

        # High frequence attention (Hi-Fi)
        if self.h_heads > 0:
            self.h_qkv = nn.Linear(self.dim, self.h_dim * 3, bias=qkv_bias)
            self.h_proj = nn.Linear(self.h_dim, self.h_dim)


    def hifi(self, x):
        B, H, W, C = x.shape
        h_group, w_group = H // self.ws, W // self.ws
        total_groups = h_group * w_group

        x = x.reshape(B, h_group, self.ws, w_group, self.ws, C).transpose(2, 3)#B,H_GROUP,W_GROUP,WS,WS,C

        qkv = self.h_qkv(x).reshape(B, total_groups, -1, 3, self.h_heads, self.h_dim // self.h_heads).permute(3, 0, 1, 4, 2, 5)
        q, k, v = qkv[0], qkv[1], qkv[2]  # B, hw, n_head, ws*ws, head_dim
        attn = (q @ k.transpose(-2, -1)) * self.scale  # B, hw, n_head, ws*ws, ws*ws
        attn = attn.softmax(dim=-1)
        attn = (attn @ v).transpose(2, 3).reshape(B, h_group, w_group, self.ws, self.ws, self.h_dim)
        x = attn.transpose(2, 3).reshape(B, h_group * self.ws, w_group * self.ws, self.h_dim)
        x = self.h_proj(x)
        return x

    def lofi(self, x):#x是完整的特征图输入
        B, H, W, C = x.shape

        q = self.l_q(x).reshape(B, H * W, self.l_heads, self.l_dim // self.l_heads).permute(0, 2, 1, 3)#(B,L_HEAD,H*W,L_DIM/L_HEAD)
        #从原输入取Q
        if self.ws > 1:
            x_ = x.permute(0, 3, 1, 2)#(B,C,H,W)
            x_ = self.sr(x_).reshape(B, C, -1).permute(0, 2, 1)#B,H*W/S*S,C
            kv = self.l_kv(x_).reshape(B, -1, 2, self.l_heads, self.l_dim // self.l_heads).permute(2, 0, 3, 1, 4)
        else:
            kv = self.l_kv(x).reshape(B, -1, 2, self.l_heads, self.l_dim // self.l_heads).permute(2, 0, 3, 1, 4)
        k, v = kv[0], kv[1]
        #K和V(B,num_head,H*W/S*S,C/num_head)，q是原尺寸，这样运算结果是原尺寸。
        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim=-1)

        x = (attn @ v).transpose(1, 2).reshape(B, H, W, self.l_dim)
        x = self.l_proj(x)
        return x

    def forward(self, x, H, W):
        B, N, C = x.shape

        x = x.reshape(B, H, W, C)

        # pad feature maps to multiples of window size
        pad_l = pad_t = 0
        pad_r = (self.ws - W % self.ws) % self.ws
        pad_b = (self.ws - H % self.ws) % self.ws
        x = F.pad(x, (0, 0, pad_l, pad_r, pad_t, pad_b))

        if self.h_heads == 0:
            x = self.lofi(x)
            if pad_r > 0 or pad_b > 0:
                x = x[:, :H, :W, :]
            return x.reshape(B, N, C)

        if self.l_heads == 0:
            x = self.hifi(x)
            if pad_r > 0 or pad_b > 0:
                x = x[:, :H, :W, :]
            return x.reshape(B, N, C)

        hifi_out = self.hifi(x)
        lofi_out = self.lofi(x)
        if pad_r > 0 or pad_b > 0:
            x = torch.cat((hifi_out[:, :H, :W, :], lofi_out[:, :H, :W, :]), dim=-1)
        else:
            x = torch.cat((hifi_out, lofi_out), dim=-1)
        #不是简单分割，而是通过linear浓缩。然后再拼接成原来维度。
        x = x.reshape(B, N, C)
        return x

  此外，还在FFN层中增加了3x3卷积和零填充来替代position embed.