pytorch梯度计算

在训练神经网络时我们有很多的需求，比如我们在训练时需要冻结某一部分网络，再比如我们需要通过一个网络两次等等，这都涉及对计算图的操作，首先通过简单的demo来看一下pytorch是怎么计算梯度的，然后我们再通过一些实例对网络进行操作

一个简单的梯度示例

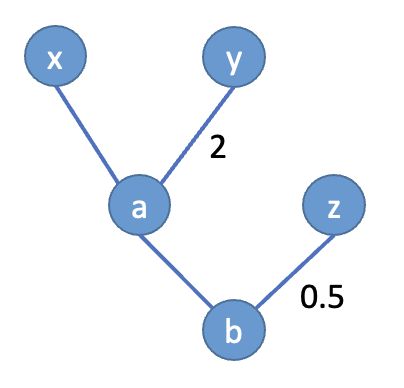
创建三个二维变量x，y，z，令

$$\begin{gathered} a=x+2y \\ b=a+0.5z \end{gathered}$$

我们画出上述计算的简单图示

假设$x=[2,1]$，$y=[1,3]$，$z=[5,2]$，计算梯度$\frac{\partial b}{\partial a}=1$，$\frac{\partial b}{\partial z}=0.5$，$\frac{\partial a}{\partial x}=1$，$\frac{\partial a}{\partial y}=2$，所以

$$\begin{gathered} \frac{\partial b}{\partial x}=\frac{\partial b}{\partial a}\ast \frac{\partial a}{\partial x}=1\ast 1=1 \\ \frac{\partial b}{\partial y}=\frac{\partial b}{\partial a}\ast \frac{\partial a}{\partial y}=1\ast 2=2 \\ \frac{\partial b}{\partial z}=0.5 \end{gathered}$$

在torch中计算时，我们需要知道一些tensor的属性：

• if_leaf：是否是叶子结点，例如x、y、z就是叶子节点
• requires_grad：是否需要计算梯度
• data：节点值
• grad：反向传播后的节点梯度
• grad_fn：节点的计算记录，从此可以得知该变量是否是一个计算结果，即是否是一个函数的输出，例如a的为Add，叶子节点xyz的为None

下面我们通过代码进行验证

注意其中有一句a.retain_grad()，这句代码是说最后也要得到a的梯度，因为torch在backward()之后只有叶子节点有梯度值，中间变量是没有的，如果想直接计算出来需要加上上述语句

import torch

''' initial xyz (requires_grad=True) ''' 
x = torch.Tensor([2, 1]).requires_grad_()
y = torch.Tensor([1, 3]).requires_grad_()
z = torch.Tensor([5, 2]).requires_grad_()

a = x + y*2
a.retain_grad()
# a = a.detach()
b = a + z/2
b.backward(torch.ones_like(x))
# b.backward(b.data)
print(x.data, x.grad)
print(y.data, y.grad)
print(z.data, z.grad)
print(a.data, a.grad)
'''
tensor([2., 1.]) tensor([1., 1.])
tensor([1., 3.]) tensor([2., 2.])
tensor([5., 2.]) tensor([0.5000, 0.5000])
tensor([4., 7.]) tensor([1., 1.])
'''

最终输出结果与我们计算的是相同的，上述代码中b.backward(torch.ones_like(x))括号中的参数维度和b的维度相同，如果没有该参数会报下述错误

RuntimeError: grad can be implicitly created only for scalar outputs

这是因为默认的backward()希望是一个标量，但是我们的b是一个二维向量，所以我们将其中传入和b维度相同的1即可（应该是默认输出的每一维度对自己的梯度为1？因为如果传入的是torch.ones_like(x)*2的话最后的梯度会变为原来的2倍）如果最后输出的是scalar，backward()不需要传入参数，默认传入的应该是torch.ones_like(torch.tensor(1))

经过验证，如果输出的b是向量，b.backward(gradient=torch.ones_like(x))其实等价于下面两句，实际上还是将b变成了标量在进行的backward

b = torch.sum(b*torch.ones_like(x))
b.backward()